应力波在树木径切面内的传播速度模型

DOI: 10.11707/j.1001-7488.20160713

文章信息

翁翔, 李光辉, 冯海林, 杜晓晨, 陈方翔

Weng Xiang, Li Guanghui, Feng Hailin, Du Xiaochen, Chen Fangxiang

应力波在树木径切面内的传播速度模型

Stress Wave Propagation Velocity Model in RL Plane of Standing Trees

林业科学, 2016, 52(7): 104-112

Scientia Silvae Sinicae, 2016, 52(7): 104-112.

DOI: 10.11707/j.1001-7488.20160713

文章历史

收稿日期：2015-06-11

修回日期：2015-12-27

作者相关文章

翁翔

李光辉

冯海林

杜晓晨

陈方翔

引用本文

翁翔, 李光辉, 冯海林, 杜晓晨, 陈方翔. 2016. 应力波在树木径切面内的传播速度模型[J]. 林业科学, 52(7): 104-112. 复制到剪切板

Weng Xiang, Li Guanghui, Feng Hailin, Du Xiaochen, Chen Fangxiang. 2016. Stress Wave Propagation Velocity Model in RL Plane of Standing Trees. Scientia Silvae Sinicae, 52(7): 104-112. DOI: 10.11707/j.1001-7488.20160713 复制到剪切板

应力波在树木径切面内的传播速度模型

翁翔, 李光辉, 冯海林, 杜晓晨, 陈方翔

浙江农林大学信息工程学院浙江省林业智能监测与信息技术研究重点实验室临安 311300

收稿日期：2015-06-11; 修回日期：2015-12-27

基金项目：国家自然科学基金项目（61272313,61302185,61472368）；浙江省自然科学基金项目（LQ13F020013,LY15F020034）；浙江省科技厅项目（2014C31044,2013C24026）

通讯作者：李光辉

摘要： 【目的】 研究应力波在不同树木径切面内传播速度的变化情况，建立传播速度模型，以期进一步认识应力波在树木径切面内的传播规律及其影响因素，为树木内部缺陷的三维成像技术提供理论依据。 【方法】 首先通过理论分析，建立应力波在树木径切面内的传播速度模型；然后以浙江农林大学植物园内8类有代表性的树种（香樟、枫香、乐昌含笑、鹅掌楸、响叶杨、悬铃木、松树、白杨）为试验材料，在样本径切面上，采用Arbotom应力波木材无损检测仪测量与径向成不同角度方向的应力波传播时间，计算不同角度方向上的应力波传播速度，并对健康样本径切面内沿方向角θ的应力波速度v_θ和径向应力波速度v₀的比值v_θ/v₀与方向角θ之间的关系进行回归分析。 【结果】 应力波在健康香樟样本径切面内的传播速度随方向角的增大而增大，径向传播速度最小，其原因是当应力波在树木内部沿径向传播时，传播方向与树木纤维方向垂直，受到细胞壁边界的阻碍较多，传播速度较慢；而随着方向角的增大，应力波传播方向与树木纤维方向逐渐平行，受到细胞壁边界的阻碍变少，传播速度逐渐增加。枫香、乐昌含笑、鹅掌楸、响叶杨4种树种的健康样本在相同方向角上的应力波传播速度大小不同，但其变化规律与香樟活力木相同。对健康样本试验数据的拟合结果为v_θ/v₀≈kθ²+1（0≤k≤1），k值取决于被测树木的物理力学参数。在所建立的回归模型中，决定系数R²均大于0.92，表明模型具有较高的拟合优度。在有缺陷的悬铃木样本试验中，径切面上方向角为-20°～-50°的应力波传播路径经过缺陷区域，其余传播路径均位于健康区域内。当应力波传播路径位于径切面的健康区域时，传播速度随方向角的变化趋势满足一元二次函数模型；但当应力波经过径切面的缺陷区域时，传播速度明显降低，不再符合正常情况下的传播速度模型。针对松树和白杨原木试样，人工设计了空洞缺陷，并对产生空洞前后的原木径切面的应力波传播速度进行了对比。最后，基于建立的径切面内应力波传播速度模型，设计了一种树木内部缺陷四向交叉检测方法，该方法能够较准确地检测木材内部缺陷的位置。 【结论】 在健康树木的径切面上，方向角θ与v_θ/v₀之间满足一元二次函数关系v_θ/v₀≈kθ²+1（0≤k≤1），对不同树种的检测结果均表明了该模型的有效性；进一步的试验证明了该速度模型对于树木内部缺陷检测具有很好的指导作用。

关键词: 应力波径切面传播速度无损检测树木

Stress Wave Propagation Velocity Model in RL Plane of Standing Trees

Weng Xiang, Li Guanghui, Feng Hailin, Du Xiaochen, Chen Fangxiang

Zhejiang Provincial Key Laboratory of Intelligent Monitoring in Forestry and Information Technology School of Information Engineering, Zhejiang A & F University Lin'an 311300

Abstract: 【Objective】 Standing trees of different species were selected as samples to study the stress wave propagation velocity pattern in the RL(radial and longitudinal)plane of wood so that the rule of stress wave propagation can be understood well, and the theoretical basis of three dimensional imaging of wood internal structure can be improved. 【Method】 Firstly, an analytical stress wave velocity model in RL plane of wood was derived. Then eight standing trees of different species(Cinnamomum camphora, Liquidambar formosana, Michelia chapensis, Liriodendron chinensis, Populus adenopoda, Platanus sp., Pinus sp., and Populus alba)at the university arboretum in Zhejiang Agricultural and Forestry University were selected as samples for nondestructive evaluation experiments. Arbotom detector was used to measure the stress wave velocity at different grain angles in the RL plane of specimens. For the healthy samples of standing tree, the regression analysis about the ratio of the velocity v_θ along the direction angle θ and the radial velocity v₀ was finished. 【Result】 In the RL plane of healthy trees, stress wave velocity increased with direction angle θ becoming larger, and the wave velocity along the radial direction was the smallest. The radial direction angle θ=0. When θ increased gradually, the stress wave velocity became faster and propagated parallel to the grain gradually. For the same direction angle θ, the stress wave velocity v_θ were different in different standing trees. Generally, the relationship between the direction angle θ and the ratio v_θ/v₀ approximated to a quadratic function v_θ/v₀≈kθ²+1(0≤k≤1), and k depended on the physical and mechanical properties of wood. For all the regression models of different samples of standing trees, the coefficient of determination R² was higher than 0.92. The regression results demonstrated the effectiveness of the analytical stress wave velocity model. In order to evaluate the effectiveness of above mentioned model, two other experiments on Platanus sp., with internal decay and log samples were finished. In the RL plane of Platanus sp., some stress wave propagation paths traversed through the decay area, and the wave velocities didn't accord with above mentioned mode for these paths. Similarly, after the test on a healthy Pinus sp., log and a healthy P.alba log, a rectangle hole was dug in the log, and ran the test again with same wave propagation path as before. Finally, based on the proposed stress wave velocity model, a four direction cross-testing method was presented, which could detect the location of internal defect of wood. 【Conclusion】 In the RL plane of healthy standing trees, the relationship between the direction angle θ and the ratio v_θ/v₀ approximated to a quadratic function v_θ/v₀≈kθ²+1(0≤k≤1). Experimental results on many standing trees of different species demonstrated the effectiveness of the stress wave velocity model. Further experiment and analysis showed that the proposed wave model could be helpful to detect the internal defects of trees.

Key words: stress wave RL plane propagation velocity non-destructive testing standing trees

应力波是指物体受到冲击后，因应力作用而产生的可在其内部传播的弹性机械波(闫在兴，2008)。在我国，应力波技术首先应用在混凝土、岩土、基桩和油气管道的性能和缺陷检测中，之后才渐渐引起林业科研人员的重视，将该技术应用到了木材无损检测领域，对应力波的传播机制、获取试验数据的手段、数据之间的相关性、不同树种之间的差异以及定性和定量识别等方面进行了深入研究，取得了大量研究成果(安源，2013)。

木材应力波无损检测技术的基本原理是利用脉冲锤敲击被测木材上的发射端传感器，使木材内部产生应力波，测量应力波传播到接收端传感器的时间，计算传播速度，通过分析应力波传播时间和传播速度的变化来确定木材的内部缺陷(Lee et al., 2003；杨学春，2004；梁善庆等，2010)。根据传播速度可以确定木材的物理力学特性(Kang et al., 2002； Brashaw et al., 2004； Ishiguri et al., 2008)，再用层析成像技术模拟出不规则树干形状并以二维图像方式直观地显示立木腐朽部位、程度、大小及形状等情况(梁善庆等，2008)。木材应力波无损检测技术与其他无损检测技术相比，具有传播距离远和能量大、抗干扰能力强、不受木材尺寸影响、无需耦合剂、对人体无害、设备小巧、携带方便等特点，已在木材物理力学性能分析、林木内部缺陷检测和古建筑木结构健康监测等领域得到了广泛应用(杨学春等，2002)。

目前，国内外对应力波在树木内部的传播理论进行了大量研究(杨学春等，2005；王立海等，2011； Li et al., 2014；冯海林等，2010；徐华东等，2014)，然而，涉及应力波在树木径切面内的传播规律研究相对较少。张厚江等(2010)对应力波在美国红松(Pinus resinosa)立木横截面和纵截面内的传播机制进行了研究，但该研究主要通过绘制应力波的传播时间等值线来进行比较测试，并未对应力波传播速度与传播方向之间的关系进行深入分析。为此，本文对健康和含缺陷树木径切面内的应力波传播速度随方向角的变化规律展开研究，以期发现应力波在树木径切面内的传播规律，为树木内部缺陷的三维成像技术提供理论依据。

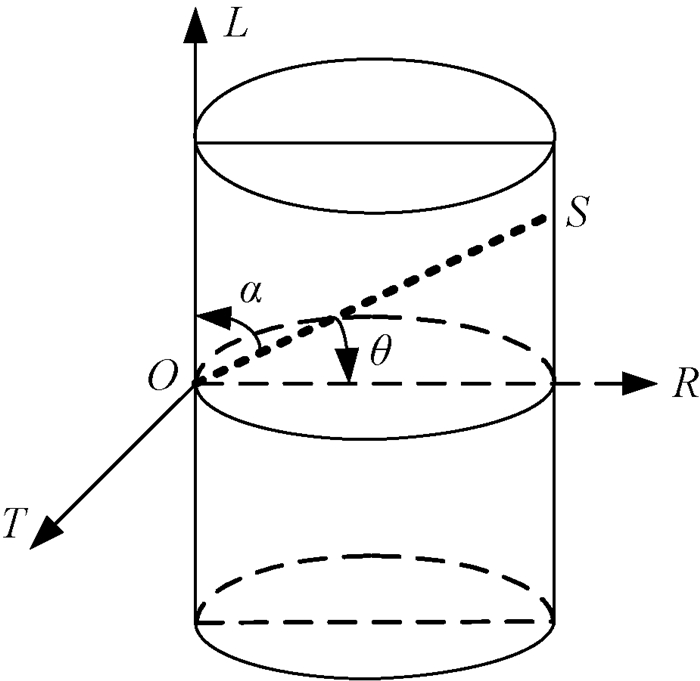
1 应力波在树木径切面内的传播过程理论

假设某段理想的树干为圆柱，建立如图 1所示以O为原点的三维坐标系，其中OR、OL、OT分别表示径向、纵向和切向，平面ROL代表径切面。进一步假设应力波在径切面内沿OS方向传播，O为信号发射端，S为信号接收端。此外，α表示应力波传播方向与纤维方向之间的夹角，θ表示径向与应力波传播方向之间的夹角，显然，α+θ=90°。

图 1 树干的三维坐标系统 Fig.1 Three-dimensional coordinate system of trunk

为了预测木材离轴的单轴压缩强度，Hankinson公式给出了一种数学模型。该公式将纤维应力或者应力波速度作为木材纹理角度的函数进行计算，当应力波在径切面内传播时，如果传播方向与木材纹理角方向之间的夹角为α，那么由Hankinson公式可以推出应力波传播速度为：

$v\left(\alpha \right)=\frac{{{v_{\rm{l}}}{v_{\rm{r}}}}}{{{v_{\rm{l}}}{{\sin }^2}\alpha +{v_{\rm{r}}}{{\cos }^2}\alpha }} \circ $

(1)

式中：v_l表示平行于纹理方向的应力波速度；v_r表示垂直于纹理方向的应力波速度(即径向传播速度)。

由于α+θ=90°，因此式(1)可以转化为：

$v\left(\theta \right)=\frac{{{v_{\rm{l}}}{v_{\rm{r}}}}}{{{v_{\rm{l}}}{{\cos }^2}\theta +{v_{\rm{r}}}{{\sin }^2}\theta }} \circ $

(2)

或

$v\left(\theta \right)/{v_{\rm{r}}}=\frac{{{v_{\rm{l}}}}}{{{v_{\rm{l}}}{{\cos }^2}\theta +{v_{\rm{r}}}{{\sin }^2}\theta }} \circ $

(3)

令 f(θ)=v(θ)/v_r，从式(3)可知，若θ=90°，则有f(θ)=v_l/v_r；若θ=0，则有 f(θ)=1。在θ=0处用二阶泰勒公式展开式(3)，得到：

$\begin{array}{l} f\left(\theta \right)=f\left(0 \right)+\frac{1}{{1!}}f'\left(0 \right)\theta +\frac{1}{{2!}}f''\left(0 \right){\theta ^2}+O\left({{\theta ^3}} \right)\\ =1+\frac{{{v_{\rm{l}}}- {v_{\rm{r}}}}}{{{v_{\rm{l}}}}}{\theta ^2}+O\left({{\theta ^3}} \right) \end{array}$

(4)

$ \approx 1+\frac{{{v_{\rm{l}}}- {v_{\rm{r}}}}}{{{v_{\rm{l}}}}}{\theta ^2} \circ $

(5)

式(4)中，O(θ³)表示泰勒展开式的余项。对于图 1所示坐标系统，假设在径切面内沿逆时针方向角度为正，沿顺时针方向角度为负。式(5)表明，比值v(θ)/v_r逼近于一条以θ=0为对称轴的抛物线，而且二次项系数介于0和1之间。

2 材料与方法 2.1 试验材料

选取浙江农林大学植物园内有代表性的健康活立木作为研究对象，包括香樟(Cinnamomum camphora)4株、枫香(Liquidambar formosana)5株、乐昌含笑(Michelia chapensis)5株、鹅掌楸(Liriodendron chinensis)3株、响叶杨(Populus adenopoda)1株和悬铃木(Platanus sp.)1株。另选取松(Pinus sp.)和白杨(Populus alba)作为原木检测试验的试样。

2.2 试验设备

采用德国Rinntech公司生产的Arbotom应力波木材无损检测仪(图 2)，该仪器包含12个传感器及主机和成像软件，能够测量传感器之间的应力波传播时间，并能够通过软件生成速度矩阵和二维断层图像。

图 2 无损检测试验设置 Fig.2 Setup of nondestructive testing experiments a.原木检测设置Setup of log detection；b.活立木检测设置Setup of standing tree’s detection.

2.3 试验方法

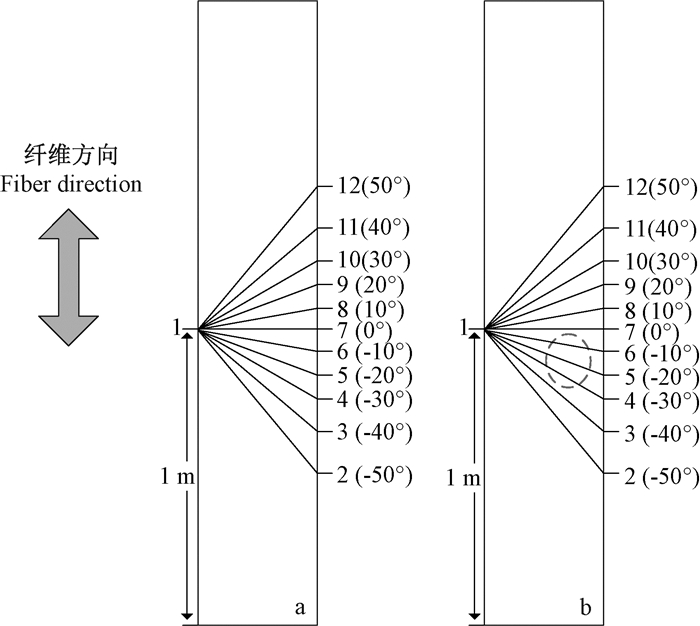
选取树木试样表面的一点O作为应力波传播的起始位置，建立如图 1所示的坐标系。依次设置好接收端的传感器，图 3描述了传感器在被测试样上的布置方案，图中矩形平面表示试样的径切面，数字表示传感器编号及布置位置，括号中的数值表示传播路径与径向所成角度。1号传感器作为应力波发射端，其他均为接收端传感器。本文设计了2组试验。

图 3 试验样本径切面上的传感器布置 Fig.3 Arrangement of sensors on experimental samples a.健康活立木样本Healthy sample of standing tree；b.有缺陷活立木样本Defective sample of standing tree.

1) 健康活立木试验(图 3a)：选取试验样本的一个径切面，在离地1 m高度处钉入1号传感器，在同样高度的直径另一端钉入7号传感器，接着分别正负2个方向每隔10°布置传感器，传感器编号为2～12号,测试角度范围为-50°～50°。使用脉冲锤敲击发射端，记录应力波传播到每个接收端的时间。

2) 有缺陷活立木试验(图 3b)：采用与健康活体试验相同的方法对有缺陷活立木试验样本进行测试。记录应力波传播到每个接收端的时间。

数据采集完成后，分别计算出不同角度方向上的应力波传播速度，利用SPSS软件进行数据分析与图形处理。

3 结果与分析 3.1 健康活立木径切面内的应力波传播速度模型 3.1.1 健康香樟活立木径切面内的应力波传播速度模型

选取4株健康香樟活立木作为试样，分别编号为1，2，3和4。用 Arbotom应力波木材无损检测仪在起始高度为1 m处按上述试验方法进行检测，方向角θ与相应的应力波传播速度如表 1所示。

表 1 健康香樟活立木径切面内不同方向的应力波传播速度^① Tab.1 Stress wave propagation velocity along different direction in RL plane of healthy C. camphora

将表 1数据应用SPSS软件绘制得到应力波传播速度散点图并进行曲线拟合，如图 4所示，4条曲线分别表示4个试样在径切面内不同角度方向上的应力波传播速度变化趋势。由图 4可知，应力波传播速度随着方向角的增大而增大，径向速度最小，整体趋势为一条开口向上的抛物线。

图 4 香樟活立木径切面内的应力波传播速度拟合曲线 Fig.4 The fitted curves of the stress wave velocity in RL plane of healthy C. camphora

为了使拟合的公式更加简便，使传播速度模型更具代表性，应用SPSS软件分别对4个试样的方向角θ与比值v_θ/v₀之间的关系进行回归分析(其中v_θ为沿方向角θ的应力波速度，v₀为径向应力波速度，即方向角θ为0°时的应力波速度)，θ采用弧度制，即1°=π/180，结果如表 2所示。在所建立的4个回归模型中，决定系数R²值均大于0.92，表明模型具有较高的拟合优度。表 2 中，y 表示v_θ/v₀，x表示方向角θ(以下相同)，可以看出，各拟合曲线的一次项系数约为0，k取决于被测试样的物理力学参数，而常数项C约等于1，即v_θ/v₀≈kθ²+1(0≤k≤1)。

表 2 健康香樟活立木径切面内v_θ/v₀与θ之间的一元二次回归模型 Tab.2 Quadratic regression model of v_θ/v₀ and θ in RL plane of healthy C. camphora

3.1.2 其他树种活立木径切面内的应力波传播速度模型

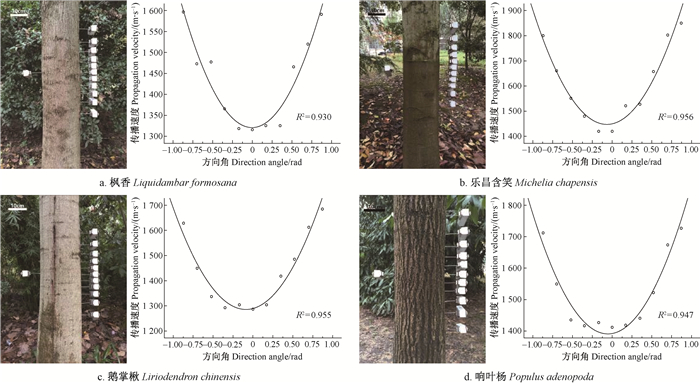
采用与香樟活立木相同的检测方法，分别对枫香、乐昌含笑、鹅掌楸、响叶杨4种树种试样相同起始高度的径切面进行检测，获取的数据经过分析处理后绘制的应力波在树木径切面内传播速度变化趋势见图 5。由图 5可知，在所检测的健康活立木中，4种树种在相同方向角上的应力波传播速度不同，但其变化规律与香樟活立木的试验结果基本相同，传播速度都是随着方向角θ的增大而增大，径向速度最小，整体趋势为一条开口向上的抛物线。分析原因为：应力波在树木内部沿径向传播时，传播方向与树木纤维方向垂直，受到细胞壁边界的阻碍较多，因此传播速度较慢；而随着方向角的增大，应力波传播方向与树木纤维方向逐渐平行，受到细胞壁边界的阻碍变少，因此传播速度逐渐增加(Dackermann et al., 2014)。

图 5 不同树种试样径切面内的应力波传播速度变化趋势 Fig.5 The stress wave propagation velocity trend lines in RL plane of different trees

为了使结论更具普遍性，将枫香、乐昌含笑样本增加至5株，但由于校内植物园树种数量有限，鹅掌楸和响叶杨分别取3株和1株。检测完成后，采用与香樟活立木试验相同的数据处理方法，将不同树种的v_θ/v₀值和方向角θ进行拟合，结果如表 3所示。由表 3可知，拟合曲线仍然满足一元二次函数关系，即y=kx²+Bx+C。通过多组试验数据分析可知，B≈0，C≈1，即v_θ/v₀≈kθ²+1(0≤k≤1)，表明该模型具有很好的拟合优度，且对不同树种都适用，能够很好地反映应力波在树木径切面内的传播规律。上述分析表明，对于选择的香樟、枫香、乐昌含笑、鹅掌楸和响叶杨等树种，应力波在健康活立木径切面内的传播模型都与本文建立的理论模型(5)非常吻合。

表 3 不同树种径切面内v_θ/v₀与方向角θ之间的一元二次回归模型 Tab.3 Quadratic regression model between v_θ/v₀ and θ in RL plane of different tree species

表 3 不同树种径切面内v_θ/v₀与方向角θ之间的一元二次回归模型

Tab.3 Quadratic regression model between v_θ/v₀ and θ in RL plane of different tree species

树种Species	拟合曲线Fitting curve	k	健康状况State of health	R²
香樟 C. camphora	y=0.379 2x²-0.021 8x+0.984 2	0.38	健康 Healthy	0.957 8
香樟 C. camphora	y=0.317 3x²+0.025 2x+1.001 7	0.32	健康 Healthy	0.988 7
香樟 C. camphora	y=0.424 1x²+0.021 0x+0.997 4	0.42	健康 Healthy	0.921 8
香樟 C. camphora	y=0.375 1x²+0.021 3x+1.033 6	0.38	健康 Healthy	0.922 9
枫香L. formosana	y=0.283 4x²+0.002 1x+1.003 9	0.28	健康 Healthy	0.929 6
枫香 L. formosana	y=0.290 4x²-0.014 1x+1.014 3	0.29	健康 Healthy	0.926 4
枫香L. formosana	y=0.356 7x²+0.020 7x+0.996 3	0.36	健康 Healthy	0.965 6
枫香L. formosana	y=0.348 6x²-0.016 1x+0.990 4	0.35	健康 Healthy	0.974 5
枫香L. formosana	y=0.341 9x²-0.001 3x+1.013 7	0.34	健康 Healthy	0.958 1
乐昌含笑 M. chapensis	y=0.367 8x²+0.048 9x+1.021 0	0.37	健康 Healthy	0.955 6
乐昌含笑 M. chapensis	y=0.381 7x²+0.046 4x+1.033 7	0.38	健康 Healthy	0.967 2
乐昌含笑 M. chapensis	y=0.439 6x²+0.039 8x+1.033 0	0.44	健康 Healthy	0.974 4
乐昌含笑 M. chapensis	y=0.387 7x²+0.047 0x+1.028 1	0.39	健康 Healthy	0.961 5
乐昌含笑 M. chapensis	y=0.436 2x²+0.033 1x+1.025 7	0.44	健康 Healthy	0.977 1
鹅掌楸 L. chinensis	y=0.377 1x²+0.066 1x+1.002 1	0.38	健康 Healthy	0.955 2
鹅掌楸 L. chinensis	y=0.415 1x²+0.016 7x+1.035 1	0.42	健康 Healthy	0.964 9
鹅掌楸 L. chinensis	y=0.365 4x²+0.064 1x+0.996 3	0.37	健康 Healthy	0.977 0
响叶杨P. adenopoda	y=0.301 6x²+0.032 3x+0.986 0	0.30	健康 Healthy	0.946 7

3.2 有缺陷活立木径切面内的应力波传播速度模型

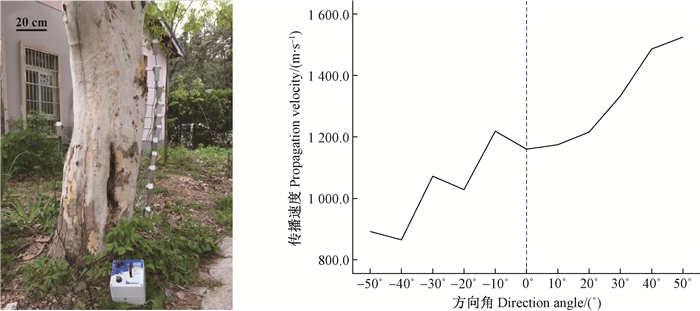
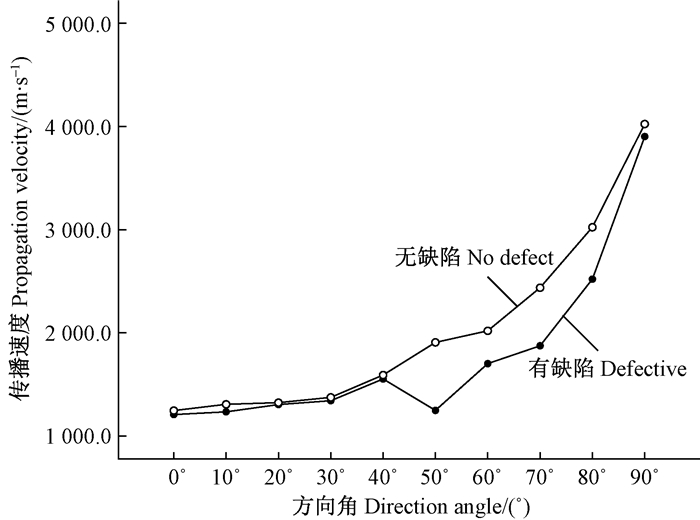
选取1株有缺陷悬铃木活立木作为试样，采用Arbotom应力波木材无损检测仪在起始高度1 m处按上述试验方法进行检测，测试角度范围为-50°～50°。该样本中下方位置有一长条形空洞，空洞处在初始高度负向区域，角度为-20°～-50°时，应力波传播路径均经过缺陷区域。

数据经过分析处理后，应用SPSS软件绘制得到应力波在树木径切面内传播速度变化趋势见图 6，图中虚线为对称参考线。由图 6可知，对称参考线两侧的应力波传播速度有很大差别，在方向角为±50°，±40°，±30°和±20°处时传播速度差别尤为明显。实际上，当θ=-20°，-30°，-40°和-50°时，应力波经过了内部空洞区域，所测传播速度分别为1 028.5，1 072.0，864.9和892.1 m·s^-1；当θ=20°，30°，40°和50°时，应力波经过了健康区域，所测传播速度分别为1 215.7，1 333.3，1 486.0和1 525 m·s^-1。通过对比可知，在树木健康部分，应力波传播速度随方向角的变化趋势仍然满足健康树木内部的传播速度模型，根据应力波的传播机制和费马原理，应力波总是沿着最短的路径传播；但当应力波传播到有缺陷区域时，其传播时间延长，传播速度明显降低，不再符合正常情况下的传播速度模型。

图 6 有缺陷悬铃木径切面内的应力波传播速度变化趋势 Fig.6 The stress wave velocity trend lines in RL plane of defective Platanus sample

4 讨论 4.1 健康原木与有缺陷原木径切面内应力波传播速度对比

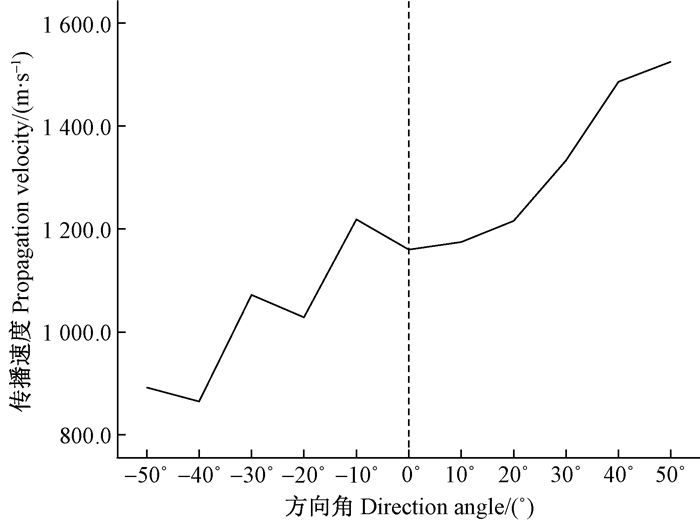
将一根健康的1.25 m长的松树原木采用上述方法进行试验，选取样本径切面右下角的一处位置放置1号传感器，取消了负方向上传感器的布置并新增了对60°，70°，80°和90°方向上应力波传播速度的检测(图 7a)，使得测试角度范围达到了0°～90°(方向角90°即代表原木纵向)，检测完成后记录数据。随后保持传感器位置不变，在原木上人工凿一个长30 cm、宽15 cm的矩形空洞(图 7b中虚线区域，方向角为50°，60°，70°和80°的应力波传播路径经过空洞，方向角为90°的应力波传播路径不经过空洞)，采用同样方法进行测试，记录数据。

图 7 原木缺陷检测的对比试验示意 Fig.7 Comparison experiment between healthy and defective logs a.健康原木 Healthy log；b.含空洞的原木 Log with cavity.

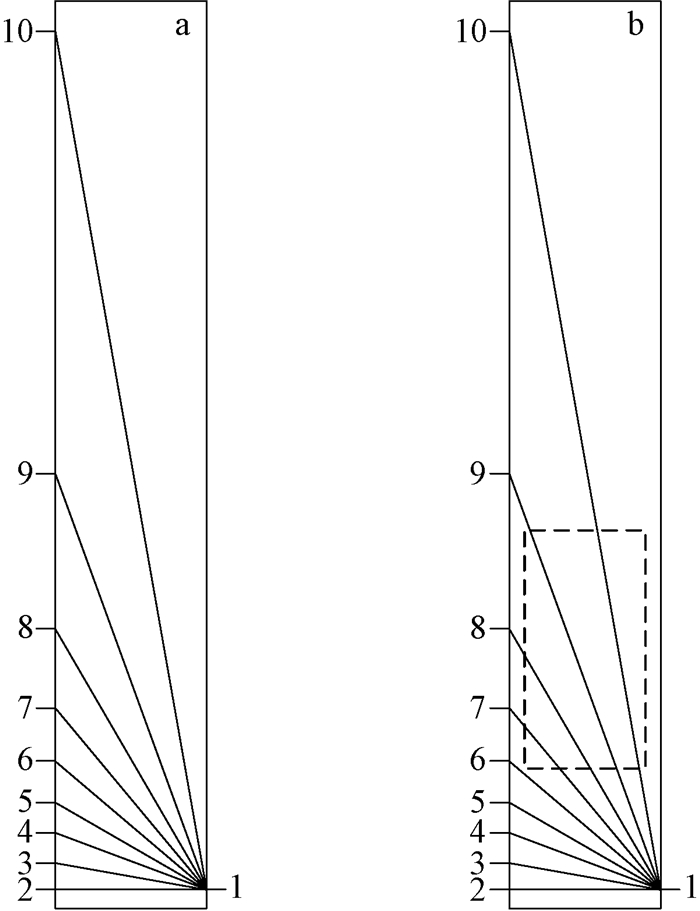
完成健康原木和含空洞原木的检测试验后，分别计算出二者在不同角度方向上的应力波传播速度，并应用SPSS软件绘制凿洞前后的应力波传播速度变化趋势，如图 8所示。

图 8 健康与有缺陷原木径切面内应力波传播速度变化趋势对比 Fig.8 Comparison of stress wave propagation velocities between healthy and defective logs

由图 7和图 8可以看出，在θ=50°，60°，70°和80°方向上，凿洞前后的应力波传播速度差异明显，分别为1 908.0，2 020.2，2 437.5，3 023.6和1 249.0，1 702.1，1 875，2 520.8 m·s^-1。由于凿洞后应力波传播经过了空洞区域，传播速度明显低于凿洞前。

为了进一步探究径切面内应力波经过健康区域和有缺陷区域的波速变化情况，另选用一根白杨原木做同样试验，传感器布置和原木凿洞位置与图 7相同，方向角为50°，60°，70°和80°的应力波传播路径经过缺陷，分析凿洞前后各角度方向上应力波传播速度化情况(表 4)。由表 4可知，在同一角度方向上，健康区域内的应力波传播速度变化不大，而经过缺陷区域后传播速度会比在健康区域降低15%以上。在树木横截面上，Wang等(2004) 研究认为，当测得某条传播路径上应力波传播时间大于其参考值为10%时，则该路径可视为经过缺陷区域。对于径切面内的应力波传播，本文针对多个树种的检测表明，在某个传播路径上，如果测得应力波传播速度与正常值相差15%以上，即可初步判断树木在该传播路径上存在缺陷。

表 4 松树和白杨原木样本径切面上不同角度方向上的应力波传播速度^① Tab.4 Stress wave propagation velocity along different direction in RL plane of Pinus sp. and P. alba log

4.2 利用应力波在径切面内的传播规律检测原木内部缺陷

基于上述统计分析获得的应力波在健康树木径切面内的传播速度模型以及内部缺陷对传播速度模型的影响情况，本文设计了一种树木内部缺陷四向交叉检测方法。以图 7b所示的松树原木缺陷为例，由于仅使用1次图 7b所示方法所检测的传播路径不足以覆盖被测径切面，因此对被测样本从多个起始点沿不同方向进行检测以获取更多数据，这样就可以通过相应的传播速度以及路径交叉分析，判断出样本内部的缺陷分布情况。从同一径切面(长方形)的4个顶点出发，分别进行4轮应力波检测，统计每轮沿不同角度方向的传播速度，并与健康参考值(本试验取表 4中的v₁为健康参考值；当健康参考值难以获得时，采用理论模型计算出来的结果作为参考值)对比，相差15%以上即视为异常，出现异常值的传播路径用红色标记，表示该路径通过缺陷区域，正常部分用绿色标记，表示该路径未通过缺陷区域。图 9描述了四向交叉检测的过程。

图 9 四向交叉检测过程(径切面) Fig.9 Scheme of four direction cross-testing in RL plane

与图 7b相对应的真实原木及其内部空洞如图 10d所示。图 9中标记为红色的路径表示经过缺陷区域，可以看出在图 9a和图 9b的检测中，路径1-7，1-8，1-9，1-10都经过了空洞区域，而在图 9c和图 9d的检测中，路径1-10经过了空洞区域。综合利用4次检测结果，可以得到图 10a所示路线图。从图 10a可以看出，传播路径c-a，c-d₇，c-d₆，c-d₅，d-b，d-c₇，d-c₆，d-c₅经过了缺陷区域。为了使定位更精确，以d-b路径为例，进行二次着色，其中b-p段和q-d段经过的路径全为绿色，即可认为该段处在健康区域，将其标记为绿色；p-o段和r-q段经过1条绿色路径和1条红色路径，认为该段处在过渡区域，将其标记为黄色；o-r段经过的路径全为红色，认为该段处在缺陷区域，将其标记为红色。依次对所有红色传播路径进行二次着色，得到的红色区域各路径边缘的交点被当成缺陷区域的边界点，依次连接起来即获得了缺陷区域的大致位置(图 10b)，最后经过填充和边缘圆滑处理后区域ABCDEF为定位结果(图 10c)。

图 10 缺陷定位结果与实际缺陷位置比较 Fig.10 Comparison between the localization results and real location of defect

在图 10c中，红色区域为缺陷定位区域，与图 10d中凿洞后的实际缺陷位置对比可以发现，二者大致吻合，说明上述方法能较准确地检测出原木内部缺陷的位置；当然如果能够增加更多角度方向的检测数据，缺陷检测结果将更精确。当第1轮应力波检测激励点1的位置确定后，该方法的检测范围随之确定，因此，当对活立木进行检测时，应结合人工经验及被检测区域的特征来确定激励点1的位置。

5 结论

本文分析了应力波在树木内部径切面内传播速度的变化规律，建立了理论模型；针对不同树种完成了应力波无损检测试验，建立了应力波在树木径切面内的传播速度模型，得到如下结论：

1) 理论分析表明，在健康树木的径切面内，沿方向角θ的应力波传播速度和径向传播速度比值v(θ)/v_r逼近一元二次函数$1+\frac{{{v_{\rm{l}}}- {v_{\rm{r}}}}}{{{v_{\rm{l}}}}}{\theta ^2}$。针对不同树种的检测试验结果表明，应力波在径切面内的传播速度随着方向角的增大而增大，当方向角为零(即沿径向传播)时，速度最小；不同树种的回归分析模型均为开口向上的抛物线，且比值v(θ)/v_r逼近一元二次函数： v_θ/v₀≈kθ²+1(0≤k≤1)。回归分析结果证明了本文理论分析模型的正确性。

2) 在健康树木中，树种仅影响应力波传播速度的大小，而不影响应力波的传播规律。本文针对同一树种的多个样本试验结果表明，香樟、枫香、乐昌含笑、鹅掌楸k值范围分别为0.32～0.42，0.28～0.36，0.37～0.44，0.37～0.42。

3) 在含有内部缺陷的树木中，应力波在径切面内的传播速度与健康树木有明显不同，经过缺陷区域的应力波传播速度会比在健康区域时小很多。

4) 基于建立的应力波在树木径切面内的传播速度模型及影响因素，本文设计了一种四向交叉检测方法，该方法可以较准确地检测树木内部缺陷的位置；如果将其与传统的三维断层成像方法相结合，有望更好地改善成像效果。

参考文献(References)

[]	安源. 2013. 基于应力波的木材缺陷二维成像技术研究. 北京:中国林业科学研究院博士学位论文. ( An Y. 2013. Two-dimensional imaging technique of wood defects based on stress wave. Beijing:PhD thesis of Chinese Academy of Forestry.[in Chinese][in Chinese]) http://cdmd.cnki.com.cn/article/cdmd-82201-1013378429.htm
[]	冯海林, 李光辉, 方益明, 等. 2010. 应力波传播模型及其在木材检测中的应用. 系统仿真学报 , 22 (6) : 1490–1493. ( Feng H L, Li G H, Fang Y M, et al.2010. Stress wave propagation modeling and application in wood testing. Journal of Simulation , 22 (6) : 1490–1493. [in Chinese] ) (0)
[]	梁善庆, 王喜平, 蔡智勇, 等. 2008. 弹性波层析成像技术检测活立木腐朽. 林业科学 , 44 (5) : 109–114. ( Liang S Q, Wang X P, Cai Z Y, et al.2008. Elastic wave tomography in standing tree decay detection. Scientia Silvae Sinicae , 44 (5) : 109–114. [in Chinese] ) (0)
[]	梁善庆, 赵广杰, 傅峰. 2010. 应力波断层成像诊断木材内部缺陷. 木材工业 , 24 (5) : 11–13. ( Liang S Q, Zhao G J, Fu F.2010. Diagnosis of internal defects of wood with stress wave tomography. China Wood Industry , 24 (5) : 11–13. [in Chinese] ) (0)
[]	王立海, 王洋, 徐华东. 2011. 弦向角对应力波在原木横截面传播速度的影响. 林业科学 , 47 (8) : 139–142. ( Wang L H, Wang Y, Xu H D.2011. Effects of tangencial angles on stress wave propagation velocities in log's cross sections. Scientia Silvae Sinicae , 47 (8) : 139–142. [in Chinese] ) (0)
[]	徐华东, 徐国祺, 王立海, 等. 2014. 原木横截面应力波传播时间等值线绘制及影响因素分析. 林业科学 , 50 (4) : 95–100. ( Xu H D, Xu G Q, Wang L H, et al.2014. Construction of stress wave time isolines on log cross section and analysis of its effect factors. Scientia Silvae Sinicae , 50 (4) : 95–100. [in Chinese] ) (0)
[]	闫在兴. 2008. 基于应力波原木内部缺陷二维图像重建的初步研究. 哈尔滨:东北林业大学硕士学位论文. ( Yan Z X. 2008. A pilot study on 2d image construction of inner-defects in log cross-section based on stress wave. Harbin:MS thesis of Northeast Forestry University.[in Chinese][in Chinese])
[]	杨学春.2004. 基于应力波原木内部腐朽检测理论及试验的研究. 哈尔滨:东北林业大学博士学位论文. ( Yang X C. 2004. Testing theories and experiments of log inner decay based on stress-wave technology. Harbin:PhD thesis of Northeast Forestry University.[in Chinese][in Chinese]) http://cdmd.cnki.com.cn/article/cdmd-10225-2004106792.htm
[]	杨学春, 王立海. 2002. 应力波技术在木材性质检测中的研究进展. 森林工程 , 18 (6) : 11–12. ( Yang X C, Wang L H.2002. Research progresses of testing wood properties using stress wave. Forest Engineering , 18 (6) : 11–12. [in Chinese] ) (0)
[]	杨学春, 王立海. 2005. 应力波在原木中传播理论的研究. 林业科学 , 41 (5) : 132–138. ( Yang X C, Wang L H.2005. Study on the propagation theories of stress wave in log. Scientia Silvae Sinicae , 41 (5) : 132–138. [in Chinese] ) (0)
[]	张厚江, 王喜平, 苏娟, 等. 2010. 应力波在美国红松立木中传播机理的试验研究. 北京林业大学学报 , 32 (2) : 145–148. ( Zhang H J, Wang X P, Su J, et al.2010. Investigation of stress wave propagation mechanism in American red pine trees. Journal of Beijing Forestry University , 32 (2) : 145–148. [in Chinese] ) (0)
[]	Brashaw B K, Wang X, Ross R J, et al.2004. Relationship between stress wave velocities of green and dry veneer. Forest Products Journal , 54 (6) : 85–89. (0)
[]	Dackermann U, Crews K, Kasal B, et al.2014. In situ assessment of structural timber using stress-wave measurements. Materials and Structures , 47 (5) : 787–803. DOI:10.1617/s11527-013-0095-4 (0)
[]	Ishiguri F, Matsui R, Iizuka K, et al.2008. Prediction of the mechanical properties of lumber by stress-wave velocity and Pilodyn penetration of 36-year-old Japanese larch trees. Holz Roh Werkst , 66 (4) : 275–280. DOI:10.1007/s00107-008-0251-7 (0)
[]	Kang H, Booker R E.2002. Variation of stress wave velocity with MC and temperature. Wood Science & Technology , 36 (1) : 41–54. (0)
[]	Lee J J, Kim K C, Bae M S.2003. Patterns of resistographs for evaluating deteriorated structural wood members. Journal of the Korean Wood Science and Technology , 31 (6) : 45–54. (0)
[]	Li G, Wang X, Feng H, et al.2014. Analysis of wave velocity patterns in black cherry trees and its effect on internal decay detection. Computers and Electronics in Agriculture , 104 : 32–39. DOI:10.1016/j.compag.2014.03.008 (0)
[]	Wang X, Divos F, Pilon C, et al. 2004. Assessment of decay in standing timber using stress wave timing nondestructive evaluation tools, a guide for use and interpretation. General Technical Report FPL-GTR-147, USDA.