文章信息
- 谢哲根, 韩国康, 童红卫, 徐军, 葛文宁, 何必庭
- Xie Zhegen, Han Guokang, Tong Hongwei, Xu Jun, Ge Wenning, He Biting
- 序列林价及其在林木资源资产评估中的应用
- Sequential Forest Price and Its Application in Forest Resources Assets Appraisal
- 林业科学, 2016, 52(6): 43-53
- Scientia Silvae Sinicae, 2016, 52(6): 43-53.
- DOI: 10.11707/j.1001-7488.20160606
-
文章历史
- 收稿日期:2015-10-30
- 修回日期:2016-03-07
-
作者相关文章
2. 浙江省林业厅计划财务处 杭州 310020;
3. 浙江省龙泉市林业局 龙泉 323700
2. Planning and Finance Division of Zhejiang Forestry Department Hangzhou 310020 ;
3. Forestry Bureau of Longquan City Longquan 323700
在推进森林资源资产化管理、深化集体林权制度改革,以及开展自然资源核算、编制自然资源资产负债表等背景下,出现了各种非交易性森林资源资产业务,并成为当前热点问题,包括林权抵押贷款、森林保险、林木生物资产核算等。例如集体林区农户的森林经营面积小,农户林权抵押贷款小规模森林资源资产评估业务多,森林资源资产评估需求量增加(谢哲根等,2012; 赖晓燕等,2014)。非交易性森林资源资产业务一般涉及的小班数量众多,虽然不直接转移产权,但同样需要以相对准确的小班林木资产评估价值为依据。所以迫切需要研究如何在较短时间内一次性完成大批量小班的林木资源资产评估问题。
林价理论中所称的立木价(狭义林价),在森林资源资产评估中一般称林木资源资产价值,林价(狭义)、立木价、林木价经常相互通用(谢哲根等,2014)。国外林木评价研究较早,20世纪以来德国出现了各种简易实用的林木评价法,年龄价值曲线法是其中之一(上由扶,1984)。国内孔繁文等(1984)最早开展“序列林价”研究,随后的序列林价研究中普遍应用成本法(张和根,1988;马双柱等,1989; 张树青等,1990;臧斌等,1991;吴承祯等,1995; 曾林,1995)。廖克服等(1996)采用“三段式”编制序列林价表,分别幼龄林、中龄林(包括近熟林)、成熟林3个阶段,相应采用重置成本法、收益现值法、市场价倒算法进行林价计算。这些研究或者侧重于编制“标准序列林价”,或者对编制结果没有进行检验,对地利条件等关键因素也没有很好处理。序列林价很少在林木资源资产评估实践中应用。
王兆君等(2009)将一次性评估大批量财产的业务称为“批量评估”(mass appraisal),利用批量评估方法对大规模的目标资产进行评估,具有降低成本和快速高效的优势,并提出将批量评估方法引入森林资源资产评估,探讨了森林资源资产批量评估操作的基本程序。目前有关森林资源资产批量评估的报道,一是应用多元线性回归分析技术建立批量评估模型(赖晓燕等,2009; 郑德祥等,2012; 胡敏荣等,2012; Liu,2012);二是运用BP神经网络方法开展森林资源资产批量评估(郑德祥等,2013; 吕丹等,2014)。赖晓燕等(2014)以中龄林为例,对多元线性回归和BP神经网络批量评估模型作了比较,后者适用范围更广,预测精度更高。目前批量评估研究存在以下不足:1)基本上是数学方法的简单应用,缺少林木资产价值变化规律研究,实用性不大。一般按幼龄林、中龄林、成熟林,分别龄组建模。胡敏荣等(2012)建立不分龄组林木资产批量评估模型,但模型中序列林价与年龄呈线性相关,这不符合林分的价值生长规律。2)模型构建过程中需要搜集大量评估案例或者交易实例的大容量样本,由于森林资产交易不公开,建模样本调查困难、搜集工作量大。3)由于立木资产交易市场不成熟、竞争不充分,并且中、幼林交易稀少,所收集交易案例的参照性不强。4)由于单纯依赖样本建模,模型更新时需要重新收集大容量样本,建模工作的低效抵消了批量评估应有的优势。
本文希望通过深化研究,建立以序列林价为理论基础的、能够实际应用于非交易性森林资源资产业务的小班林木资源资产评估模型。为了顺利开展大批量小班林木资产同时一次性评估,必须对全部拟评估小班提供系统性的、统一的评估方法,并对各种特殊林况实物量数据的小班(如大径材成熟林小班)也能作出准确的价值计算。为此需要系统解决以下问题:1)建立适用的、反映林木价值生长过程和变化规律的评估模型。由于森林经营过程中自然生长与人工措施相交织,森林资源资产是生物资产,价值变化规律比较复杂。序列林价能够描述林木价值生长过程,是开展大批量小班林木资源资产评估的理论基础。2)全生长过程建模,而不是“三段式”分龄组建模,或者仅对全生长过程中的某一个阶段(龄组)建模,将完整的林分生长过程人为分段割裂。3)综合应用成本法、收益法、市场法3种评估方法,开展模型检验,提高评估结果可靠性。4)利用多源数据建模,避免单纯依赖大容量交易实例样本,提高建模工作的可操作性和建模效率。
1 研究地概况龙泉市是我国南方重点林区县之一,是浙江省最大的林区县(市),素有“浙江林海”之称。森林资源是龙泉市重要的生产要素,农民生活的重要保障和农民增收的重要源泉。全市土地面积30.4 万hm2,其中林业用地26.6 万hm2,占86.5%。森林蓄积量1 456万m3,森林覆盖率84.2%。全市约23万农民,人均拥有林地1.15 hm2,收入的60%来自林业及相关产业。
龙泉市积极深化林改,取得了一些成效。全市集体山林经营权落实到户的比例达到82.1%,农户森林经营积极性提高。2009年以来开展了农户经营权勘界及林权信息采集建档工作,建成全市农户森林资源地理信息系统和农户林权数据库,形成了“一户一证一图一表一卡”的“林权身份证”(即林权IC卡),图、表、册一致,方便开展林权信息查询、林权变更登记管理。以林权抵押为手段,加强银林合作,拓展林业投融资新渠道,农户林权抵押贷款基础较好。但目前“评估难”等问题逐渐显露,阻碍林权抵押贷款等深度林改工作进一步推进。
2 研究方法Wagniere(2011)总结了经营者拥有产权的森林价值(非公益效益)评估计算方法,指出自从1804年德国林学家Cotta提出现金流折现方法以来的200多年历史中,森林评价理论没有实质性改变,认为森林价值评估问题主要是实践问题,森林价值评估的能力取决于对森林价值评估所有必要知识的掌握程度;森林价值评估的知识划分为客户需求、评估标准、可靠的评估技术、森林资源和林产品数据资料4个知识领域,对应森林价值评估的4方面能力,即提供客户所需的森林价值,符合相关会计准则,确保应用适当的评估技术,考虑所有相关的森林产品和市场数据。
本文着重探讨评估技术,研究方法是分步解决林价主要影响因素对林木资源资产价值的贡献,构建结构化林木资产评估模型。首先是林分年龄因子对林木资源资产价值影响,通过研究参照林分序列林价模型,探索林木资源资产价值生长规律;其次是各个小班的具体林分状况不同对林木资产价值影响,包括林分质量因子和林分地利条件不同对林木价值的影响,探索给定年龄时不同林分状况的林木资源资产价值变化规律。建模过程中综合运用递推算法、回归方法、仿真模拟方法。
2.1 建模数据来源利用多源数据建模。一是森林资源规划设计调查数据。龙泉市共有23 858个杉木林小(细)班,林分生长模型的建模数据为小班的年龄、平均胸径、平均树高、单位面积蓄积量。二是通过实地调查获得的数据,包括1)参照林分序列林价计算用的当地林业生产技术经济指标数据:第1,2,3年营造林投入成本分别为8 505,1 740,1 350元·hm-2,每年管护工资75元·hm-2; 2)木材价格数据,龙泉市岩樟乡等高山区杉木质量好,胸径10,14,20,35 cm的杉原条伐区堆场路边价分别为830,1 150,1 540,1 970 元·m-3; 3)小班林木资产评估模型检验数据,调查搜集了研究地98个近期的杉木林“判青山”正常交易案例。三是模拟数据。正常步行速度3.5 km·h-1,负重步行速度2.5 km·h-1,模拟具体林分小班由于地利条件(集材路程)不同造成的森林经营成本、采伐集材成本差异,以及对林木资产价值影响。
2.2 参照林分序列林价模型设计 2.2.1 参照林分确定序列林价研究需要设定某种立地条件和地利条件、森林经营水平条件。相关研究文献均设定中等森林经营水平,但选择何种立地条件林地则有不同观点,一是以劣等地为基准(张汝淼等,1988;张和根,1988;马双柱等,1989),二是以中等立地为标准(曾林,1995)。计划经济时代森林资源无价,为了测算合理的木材价格水平、确定木材定价标准,林价水平研究须以劣等地为基准。但目前市场经济条件下,为其他林分提供价值参照物的序列林价研究,宜以中等立地和中等地利条件为基础,不仅方便建模、方便使用,还可避免“标准林分”等定义上的苛求。
本文序列林价研究以中等立地、中等地利(设定为集材路程1 km)、中等经营水平的林分生长过程、营林生产成本和经济收益为基础。该平均状态的林分称为“参照林分”,相应的序列林价称为“参照林分序列林价”。
2.2.2 序列林价递推公式序列林价意指林价在林木生长过程中随时间的变化在各时点(年度)上的反映(孔繁文等,1984);序列林价是指立木价格,它是运用林木生产费用和林木生长规律而确定的各个时点(年)上的价格(臧斌等,1991)。
成本法是林价测算的基本方法。在漫长的营林生产周期里,凝结在单位面积森林上的价值量,习惯上是以年为单位来计算,可以用数学方法来描述立木价值形成过程(廖士义等,1983)。孔繁文等(1984)提出成本法的序列林价计算公式,其后序列林价研究大多以此公式为基础,并增加抚育间伐因素(马双柱等,1989;张树青等,1990)。
廖克服等(1996)对幼龄林、中龄林和近熟林、成熟林3个阶段,分别应用成本法、收益法、市场价倒算法计算序列林价,然后取幼龄林的后半阶段与中龄林的前半阶段对结点进行线性修匀。但是“三段法”分段建模存在的缺陷是,幼龄林后半阶段与中龄林前半阶段的时期太长,序列林价修匀操作主观性强。
本文采用递推算法,分别应用重置成本法、收益现值法进行全生长过程建模,能观察比较2种方法计算结果的差异和合理性,并能通过观察序列林价曲线变化情况确定最佳修匀点。假定造林、幼林抚育、林地租金等投入成本发生在年初,间伐、主伐成本和收入发生在年底。采用1 年生苗木造林,造林第1 年林分年龄为2 年生。那么可推导设计出相邻2年之间的序列林价递推公式。
重置成本法序列林价递推公式:
| ${{T}_{2}}=({{C}_{1}}+{{B}_{c}}+{{B}_{r}})\times \left( 1+p \right)\times \left( 1+r \right);$ | (1) |
| $\begin{align} & {{T}_{a}}=[{{T}_{a-1}}+({{C}_{a-1}}+{{B}_{c}}+{{B}_{r}})\times \\ & \left( 1+p \right)]\times \left( 1+r \right)-{{M}_{a}}\times {{Q}_{a}}\times [{{A}_{a}}-{{L}_{a}}\times \\ & \left( 1+p \right)]\text{ }\left( a=3,4,\ldots ,u \right)\circ \\ \end{align}$ | (2) |
式中:Ta为a年生林分年末(间伐后)序列林价(元·hm-2);a 为林分平均年龄(a);u为林木主伐年龄(a);Ca为a年生林分营造林成本(元·hm-2),包括劳动工资、种苗费等,不含地租;Bc为森林管护等年间接费用(元·hm-2);Br为年地租(元·hm-2);Ma为a年生林分的间伐林木蓄积(m3·hm-2);Qa为a年生林分的间伐材综合出材率(%);Aa为a年生林分的间伐材木材综合价(元·m-3);La为a年生林分的间伐材木材采集生产成本(元·m-3);p为林业生产成本利润率(%);r为折现率(%)。
收益法序列林价递推公式:
| ${{T}_{u}}={{V}_{u}}\times {{Q}_{u}}\times [{{A}_{u}}-{{L}_{u}}\times \left( 1+p \right)];$ | (3) |
| $\begin{align} & {{T}_{a}}=\{{{T}_{a+1}}+{{M}_{a+1}}\times {{Q}_{a+1}}\times [{{A}_{a+1}}-{{L}_{a+1}}\times \\ & \left( 1+p \right)]\}/\left( 1+r \right)-({{C}_{a}}+{{B}_{c}}+{{B}_{r}})\times \\ & \left( 1+p \right)\text{ }\left( a=u-1,u-2,\ldots ,2 \right)\circ \\ \end{align}$ | (4) |
式中:Tu为参照林分主伐年龄时单位面积林木资产价值(元·hm-2);Vu为参照林分主伐年龄时单位面积蓄积量(m3·hm-2);Qu为主伐材综合出材率(%);Au为主伐材综合价(元·m-3);Lu为主伐材采集生产成本(元·m-3)。其他符号同前。
收益法序列林价递推公式以参照林分成熟林林木资产价值为基础,成熟林林木资产采用木材市场价倒算法评估(式(3))。
2.2.3 参照林分生长与收获模型式(2)、(3)、(4)中涉及间伐、主伐木材产量与收入。需要建立林分生长与收获模型,确定各年龄时的平均胸径、平均树高、立木蓄积量、采伐蓄积量,再根据出材率、木材价格便可计算木材产量、木材销售收入。
2.2.4 生产函数与投入成本用材林森林经营通过林地、生产资料、人工劳动等投入,以及经过长时期的林木自然生长过程,才能形成蓄积量,通过间伐、主伐获得木材产品。整地、造林、抚育等营林投入应该是有效投入,以取得最大的经济效果。投入不足达不到应有的产量水平;投入过度则是无效投入,产生无效费用。如果将无效费用计算在内,就可能高估供方价格水平(刘伟平,1995)。
森林经营过程中各年度的投入、相应的生长量和收益构成林分经营的投入产出关系,类似于生产函数。但是,各年度的投入与产量之间难以建立函数关系式或者回归经验公式。虽然不能建立定量的关系式,但林分序列林价模型研究需要引入生产函数理论,理性分析,科学、合理地评判营林技术措施,审慎确定有效投入、相应合理的产量水平,准确调查测算与参照林分产出相对应的投入成本,为序列林价计算奠定基础。
2.2.5 林龄价值系数林龄价值系数就是参照林分各年龄的林价与主伐年龄的林价对比的系数。各地位级林分的林龄价值系数曲线差别并不大(井上由扶,1984)。所以,相比序列林价曲线,林龄价值系数曲线具有一般性、通用性,可以认为参照林分林龄价值系数曲线普遍适用于同一类型的林分。林龄价值系数法对于众多的不同林龄的林分进行大批量林木资产评估时应用性更强,如果已知主伐年龄林价(比较容易计算),用林龄价值系数乘以主伐年龄林价即可求算某林龄林分的林价。
2.3 小班林木资产评估模型设计根据按质论价、优质优价的市场定价原则,具体小班林木资源资产评估需要考虑该小班现实林分的特殊因素。具体林分(小班)立木价的特殊构成因素包括树种、年龄、胸径、树高、单位面积株数或蓄积量、立地质量、地利条件(主要是交通)等(谢哲根等,2014)。
小班林木资产评估采用参照林分林价调整法。小班林木资产评估模型中引入的调整因子之间应相互独立,尽量避免相关而造成重复调整,所以调整因子并非越多越好。
2.3.1 成熟林小班林木资产评估待估成(过)熟林小班林木资源资产采用参照林分成熟林林木价调整法评估。参照林分成熟林林木价即序列林价最后年份的林木价。主伐年龄以后林木具备采伐利用条件,林分年龄不必作为调整因子。以直接影响成熟林小班林木资产价值的主要林分质量因子作为调整因子,包括集材路程、林分平均胸径、单位面积蓄积量。集材路程决定木材采集成本。林分平均胸径影响木材价格、出材率。单位面积蓄积量直接影响木材数量。
待估杉木成熟林小班林木资源资产评估公式:
| ${{T}_{\text{ng}}}={{k}_{\text{W}}}{{k}_{\text{D}}}{{k}_{\text{V}}}{{T}_{u}}\circ $ | (5) |
式中:Tng为待估成(过)熟林小班林木资产评估值(元·hm-2);kW为集材路程调整系数;kD,kV分别为成熟林小班的林分平均胸径调整系数、单位面积蓄积调整系数。其他符号同前。
集材路程调整系数应建立回归方程,准确反映经营与采集搬运成本对林木资产价值的影响。
由于待估成(过)熟林小班林分年龄不一定刚好是主伐年龄,各小班之间林分年龄差别大,林分平均胸径调整系数、单位面积蓄积量调整系数应分别建立回归方程,避免简单地采用比例法。
2.3.2 主伐年龄前未成熟林小班林木资产评估主伐年龄前的林分包括幼龄林、中龄林和近熟林,小班林木资产采用参照林分序列林价调整法进行评估。林分平均胸径小于5 cm时,调整因子有年龄、单位面积保存株数、平均树高、集材路程;林分平均胸径达到5 cm以上时,调整因子有年龄、平均胸径、单位面积蓄积量、集材路程。其中平均树高、单位面积蓄积量既反映小班的林分质量状况,又反映小班立地质量高低。
以参照林分序列林价和林分因子生长过程为基础,年龄调整因子采用年龄价值系数法,其他调整因子采用相应调整指数,待估未成熟林小班林木资产评估公式:
| ${{T}_{na}}={{k}_{\text{W}}}{{k}_{\text{D}}}_{a}{{k}_{\text{H}a}}{{k}_{\text{N}a}}{{k}_{\text{V}a}}{{T}_{a}}={{k}_{\text{W}}}{{k}_{\text{D}}}_{a}{{k}_{\text{H}a}}{{k}_{\text{N}a}}{{k}_{\text{V}a}}{{k}_{a}}{{T}_{u}};$ | (6) |
| ${{k}_{\text{D}}}_{a}=\left\{ \begin{matrix} 1 & ({{D}_{\text{n}a}}<5) \\ {{D}_{\text{n}a}}/{{D}_{\text{n}a}} & ({{D}_{\text{n}a}}\ge 5) \\ \end{matrix} \right.;$ | (7) |
| ${{k}_{\text{H}}}_{a}=\left\{ \begin{matrix} {{H}_{\text{n}a}}/{{H}_{\text{g}a}} & ({{D}_{\text{n}a}}<5) \\ 1 & ({{D}_{\text{n}a}}\ge 5) \\ \end{matrix} \right.;$ | (8) |
| ${{k}_{\text{N}}}_{a}=\left\{ \begin{matrix} {{N}_{\text{n}a}}/{{N}_{\text{g}a}} & ({{D}_{\text{n}a}}<5) \\ 1 & ({{D}_{\text{n}a}}\ge 5) \\ \end{matrix} \right.;$ | (9) |
| ${{k}_{\text{V}}}_{a}=\left\{ \begin{matrix} 1 & ({{D}_{\text{n}a}}<5) \\ {{V}_{\text{n}a}}/{{V}_{\text{g}a}} & ({{D}_{\text{n}a}}\ge 5) \\ \end{matrix} \right.\circ $ | (10) |
式中:Tna为幼龄林、中龄林和近熟林小班立木资产评估值(元·hm-2);Ta为参照林分a年生林木价;ka为a年生的年龄价值系数;kDa,kHa,kNa,kVa分别为未成熟林小班的林分平均胸径调整指数、平均树高调整指数、单位面积株数调整指数、单位面积蓄积量调整指数;Dna,Hna,Nna,Vna分别为a年生待估未成熟林小班的林分平均胸径(cm)、平均树高(m)、单位面积株数(株·hm-2)、单位面积蓄积量(m3·hm-2);Dga,Hga,Nga,Vga分别为参照林分a年生的林分平均胸径(cm)、平均树高(m)、单位面积株数(株·hm-2)、单位面积蓄积量(m3·hm-2)。其他符号同前。
由于待估未成熟林小班的林木价值评估是以参照林分在相同年龄上的序列林价为参考,式(7)—(10)的林分平均胸径调整指数、平均树高调整指数、单位面积株数调整指数、单位面积蓄积量调整指数采用简单比例法具有合理性。
2.4 小班林木资产评估模型检验调查正常交易的市场交易实例样本,对小班林木资产评估模型进行适用性检验,包括模型估算值与样本实际值的差异显著性置信椭圆F检验、模型使用精度检验。检验指标包括F检验统计量、总相对误差、平均相对误差、平均相对误差绝对值、估计精度,具体计算公式详见相关文献(曾伟生等,2011;尹惠妍等,2014;施恭明等,2015)。
模型适用性F 检验以小班林木资产评估模型计算的估算值为自变量x,样本实际值为因变量 y,如果二者之间的线性回归方程y=A+Bx参数(A,B)与(0,1)没有显著差异(F≤F0.05),则可以判定评估模型是适用的;如果差异显著(F>F0.05),则评估模型不适用。
模型使用精度检验的总相对误差、平均相对误差指标反映评估模型系统偏差情况,二者一般控制于一定的数值范围内(如±5 %或±10 %),趋于0 时模型效果最好;平均相对误差绝对值指标反映单个估计值的精度,即每个样本点距评估模型曲线的相对平均误差;估计精度指标反映平均估计值的精度。
2.5 小班林木资产评估模型更新如果劳动工资水平、木材价格水平、利率水平等市场条件变化不大,只要重新计算主伐年龄时参照林分林木资产评估值[式(3)],就能通过林龄价值系数更新序列林价,再利用待估小班林木资产评估公式[式(5)、式(6)],实现小班林木资源资产动态评估。
如果林分生长过程和市场条件变化大,那么需要重新建模,全面更新林木资产评估模型参数,包括林分生长与收获模型、参照林分序列林价表,以及集材路程、林分平均胸径、单位面积蓄积量等调整系数回归方程中的参数。
3 结果与分析 3.1 参照林分序列林价计算结果 3.1.1 杉木用材林参照林分生长与收获模型以杉木用材林为例,把龙泉市范围内杉木林平均生长过程视作中等立地、中等经营水平的林分生长过程,利用森林资源规划设计调查小班数据建模。龙泉市森林资源规划设计调查采用总体抽样控制、小班调查目测为主结合辅助实测和一定比例的标准地实测方法,并且经过县级、省级检查组实地抽查小班进行验收,小班数据比较可靠。与建立平均生长过程模型相对应,将小班单位面积蓄积量、平均树高、平均胸径3个林分因子分别按年龄统计平均值(胸径为均方平均直径),然后利用年龄、林分因子平均值成对数据绘制散点图,剔除趋势异常点后形成生长模型拟合样本数据。经非线性回归拟合,得到龙泉市杉木林分平均状态的生长模型,包括单位面积蓄积量-年龄模型[式(11)]、林分平均树高-年龄模型[式(12)]、林分平均胸径-年龄模型[式(13)]。
| $\begin{align} & {{V}_{a}}=142.91exp(-5.837\text{ }2{{e}^{-0.117\text{ }84a}})\text{ }\left( a\ge 10 \right) \\ & \left( 样本数26{{R}^{2}}=0.976\text{ }08 \right); \\ \end{align}$ | (11) |
| $\begin{align} & {{H}_{a}}=10.624exp(-4.156\text{ }1{{e}^{-0.161\text{ }68a}})\text{ } \\ & \left( 样本数32{{R}^{2}}=0.978\text{ }62 \right); \\ \end{align}$ | (12) |
| $\begin{align} & {{D}_{a}}=17.063(1-1.378\text{ }1{{e}^{-0.069\text{ }892a}}) \\ & \left( 样本数27{{R}^{2}}=0.971\text{ }66 \right)\circ \\ \end{align}$ | (13) |
式中:Va为a年生林分单位面积蓄积量(m3·hm-2);Ha为a年生林分平均高(m);Da为a年生林分平均胸径(cm)。
然后再根据平均单株立木材积(实验形数法,杉木实验形数取0.42)导算出单位面积林木株数-年龄模型[式(14)]。由于集体林经营方式相对粗放,间伐年龄比较灵活,林分总体平均情形下,前后2年株数差即为间伐株数[式(15)]。
| ${{N}_{a}}=\left\{ \begin{array}{*{35}{l}} {{V}_{a}}/\left[ 0.000\text{ }032\text{ }987{{D}^{2}}_{a}\left( {{H}_{a}}+3 \right) \right] & \left( a>10 \right) \\ 3\text{ }165 & \left( a\le 10 \right) \\ \end{array} \right.;$ | (14) |
| ${{N}_{Ca}}={{N}_{a-1}}-{{N}_{a}}~\circ $ | (15) |
式中:Na为a年生林分单位面积株数(株·hm-2);NCa为a年生林分单位面积间伐株数(株·hm-2)。
3.1.2 相关参数与林地地租木材出材率参考《浙江省单株立木出材率表》,确定不同平均胸径林木的综合材出材率。森林经营与采伐成本利润率取15%。由于采用的重置成本和价格均为现时物价水平,收入与支出的物价为同一时点,不存在通货膨胀因素,所以采用的折现率含经济利率(2%~3%)和风险率(1%~2%)2部分,经分析并按谨慎性原则,折现率取5.25%。
利用营林和采伐各项技术经济指标、林分生长与收获模型,采用林地期望价公式计算得出林地价,再根据林地价和折现率便可计算得到当地杉木用材林参照林分的林地年地租609 元·hm-2。
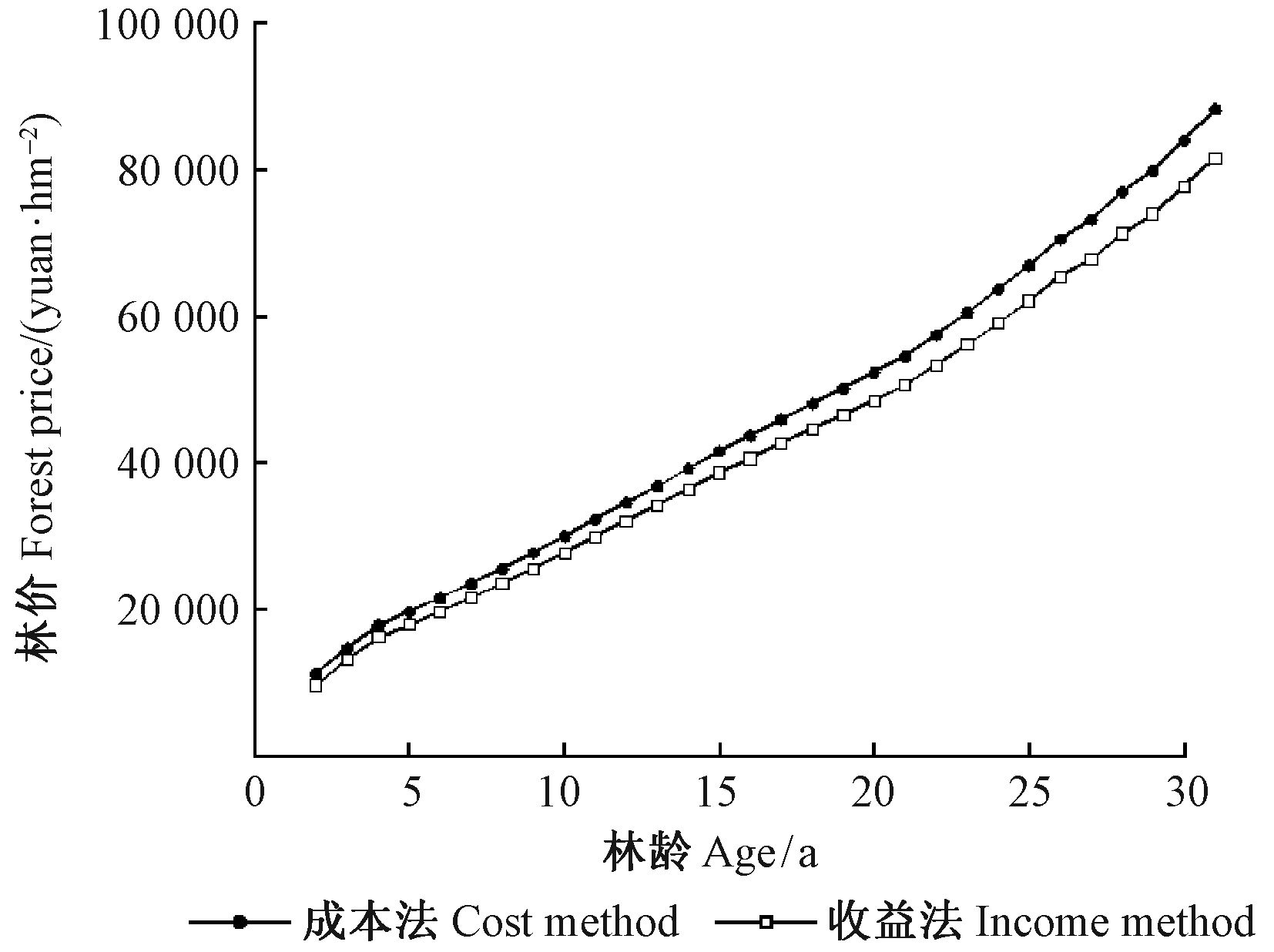
3.1.3 杉木用材林参照林分序列林价根据参照林分各项技术经济指标、生长与收获模型、相关参数,按照递推公式(1)、式(2)得到成本法计算的杉木林参照林分序列林价,按照递推公式(3)、式(4)得到收益法计算的序列林价(图 1)。由于通过引入生产函数理论,考虑了森林生长经营投入与产出的匹配性,2种方法计算的单位面积序列林价变化趋势比较一致,能够相互验证,具有较好的合理性和可靠性。
|
图 1 成本法、收益法计算的杉木林参照林分全生长过程序列林价曲线 Fig.1 Curves of sequential forest price of Chinese fir reference stand calculated by cost method and income method during the whole growth process |
综合比较计算结果,最终确定杉木林参照林分序列林价。成本法、收益法计算的杉木林参照林分序列林价曲线在6 年生、7 年生时靠近,并且趋势平缓,此处最容易修匀,考虑序列林价曲线的平滑性要求,最佳修匀点应该是林龄6 年生、7 年生处,即5 年生以前林分序列林价采用成本法计算结果,8 年生以后采用收益法计算结果,6 年生、7 年生采用修匀值。从造林至主伐年龄期间全生长过程的序列林价详见表 1。单位蓄积表示的序列林价通过单位面积序列林价和林分蓄积量计算,详见图 2。
|
|
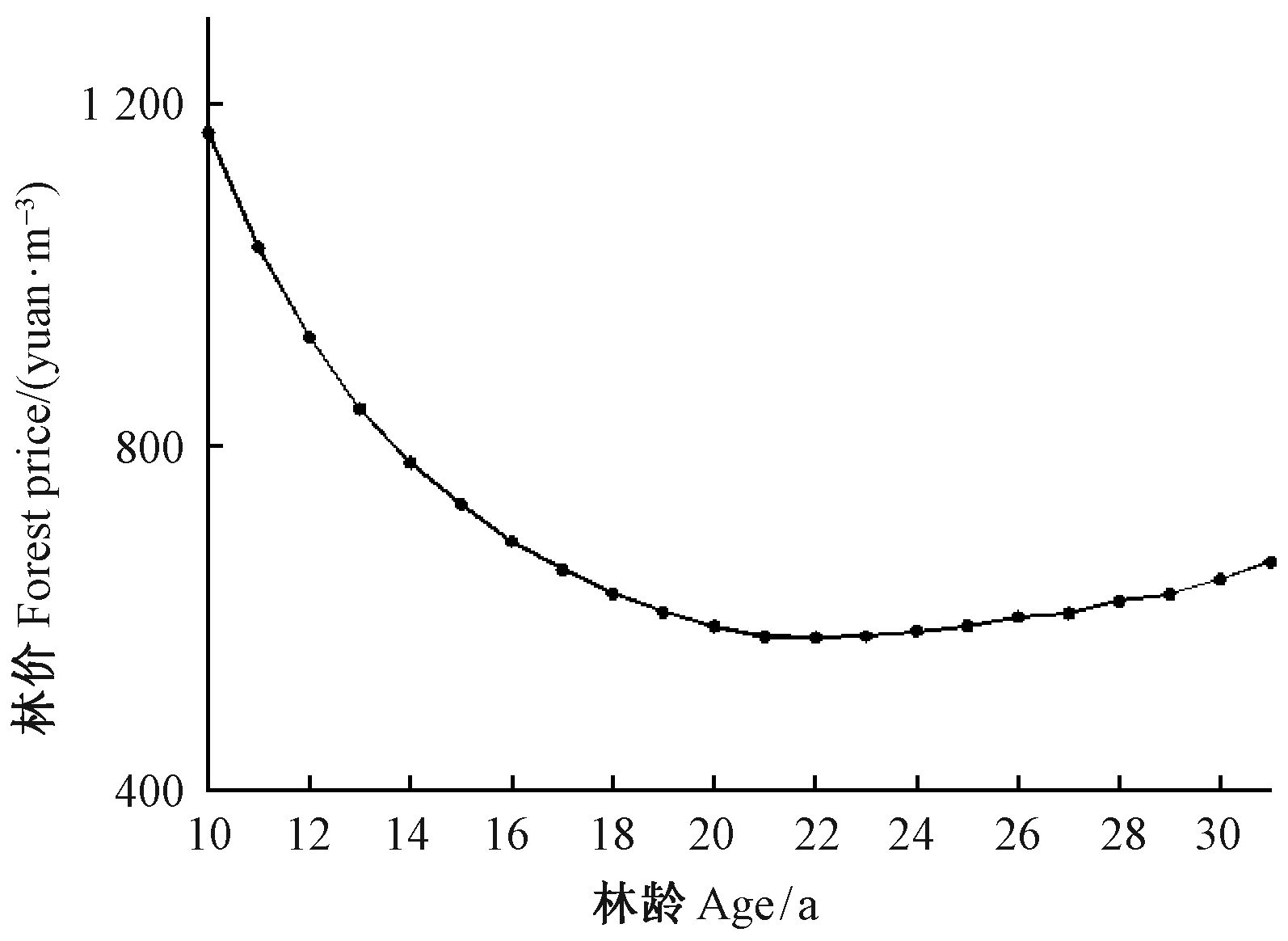
|
图 2 杉木林参照林分单位蓄积序列林价曲线 Fig.2 Curve of sequential forest price per unit stock volume of Chinese fir reference stands |
从图 1、图 2可见,杉木林分单位面积序列林价曲线大体呈指数形、单位蓄积序列林价曲线呈反“J”形。杉木林单位蓄积序列林价的变化趋势,先是逐年递降,前期的下降速度比较快,中期下降速度减缓,出现单位蓄积林价最低点,然后呈平缓上升趋势。林木胸径随年龄增大而增大,木材价格随径级增大而增加,所以木材价格随林木年龄增大而增加。可见立木林价与木材价格是不同的,杉木林单位蓄积表示的序列林价随林龄的变化趋势与木材价格随年龄的变化趋势相反。单位蓄积序列林价动态规律与孔繁文等(1984)的研究结论相同。
3.2 小班林木资产评估模型及应用结果 3.2.1 集材路程调整系数经验模型成熟林、未成熟林林木资产评估均需要考虑集材路程调整系数,因幼龄林未来将转化为成熟林。评估实务中幼龄林林木资产一般采用重置成本法评估,由于地利条件越差造林成本和森林经营成本越高,如果不考虑集材路程调整则会造成地利条件越差而林木资产价值越高的错误结果。
集材路程决定林业生产中采伐木材的搬运成本,伐区采集成本对用材林经济价值影响很大。考虑到高质量的交易实例样本数据采集困难,从样本数据中分离出集材路程对林木资产价值的影响也困难,目前难以直接通过交易实例样本建立适用的集材路程调整系数回归模型。所以先开展伐区生产成本模拟,再回归分析,建立集材路程调整系数经验模型。限于篇幅,仅作简要说明。
伐区生产工序包括砍伐、打枝、伐倒木搬运归集。通过正常步行速度、负重步行速度、日劳动工资等调查数据,设计伐区采集成本模拟函数,模拟计算具体林分小班由于地利条件(集材路程)不同造成的采伐、集材成本差异,以及对林木资产价值影响,得到各种集材路程相应的林木资产价值调整系数的模拟数据。然后回归分析,建立杉木林小班林木资产价值集材路程调整系数回归方程[式(16)]。由于伐区采集成本模拟是通过模拟函数实现的,林木资产价值的集材路程调整系数回归方程拟合确定系数(R2)高。
| $\begin{align} & {{k}_{\text{W}}}=1.217\text{ }9-0.217\text{ }35W \\ & (\text{样本数}30{{R}^{2}}=0.999\text{ }98)\circ \\ \end{align}$ | (16) |
式中:W为小班集材路程(km)。其他符号同前。
小班林木资产评估中地利条件比较难以处理,本文引入集材路程调整系数回归方程,可以定量处理地利条件对林木资产价值的影响,开展大批量小班林木资产评估时能够实现简便、快捷计算。
3.2.2 成熟林小班林分平均胸径、单位面积蓄积量调整系数经验模型同样,通过模拟计算得到林分不同平均胸径相对应的林木资产价值调整系数的模拟数据、不同单位面积蓄积量相对应的林木资产价值调整系数的模拟数据,再经回归分析,建立杉木成熟林小班林木资产价值的林分平均胸径调整系数回归方程[式(17)]、单位面积蓄积量调整系数回归方程[式(18)]。确定系数(R2)高的原因是利用模拟数据进行回归方程拟合。
| $\begin{align} & {{k}_{\text{D}}}\text{=}2.301\text{ }3\left\{ 1-\exp \left[ {{\left( -\frac{D}{18.362} \right)}^{2.352\text{ }6}} \right] \right\} \\ & \left( \text{样本数}26\text{ }{{R}^{2}}0.996\text{ }94 \right); \\ \end{align}$ | (17) |
| $\begin{align} & {{k}_{\text{V}}}=-0.000\text{ }014\text{ }489+0.008\text{ }134\text{ }1{{V}_{\text{n}}} \\ & (\text{样本数}30\text{ }{{R}^{2}}0.999\text{ }98)\circ \\ \end{align}$ | (18) |
式中:D为待估成熟林小班的林分平均胸径(cm);Vn为待估成熟林小班的林分单位面积蓄积量(m3·hm-2)。其他符号同前。
从式(17)可见,林分平均胸径调整系数与平均胸径之间的关系并非简单的线性关系。成、过熟林小班之间林分平均胸径的变幅大,林分平均胸径通过出材率和木材价格对林木价值产生较大影响。通过建立相对准确的林分平均胸径调整系数经验方程,达到比较客观地反映因胸径大小而引起的立木价值变化,从而提高成、过熟林小班林木资产评估精度。
3.2.3 小班林木资产评估模型的实践应用利用式(5)、式(16)—(18),能够对杉木成、过熟林小班林木资产作出快速评估。利用式(6)—(10)和式(16),能够对主伐年龄前的未成熟林小班林木资产作出快速评估。
本文研究的小班林木资产评估模型应用到龙泉市岩樟乡芭蕉村,对该村全部杉木用材林小班的林木资源资产作出评估。将林权信息化小班的林分调查因子代入相应的评估模型,计算得到各农户杉木用材林小班林木资产明细表;按户汇总得到各农户杉木用材林林木资产,如某个农户杉木用材林小班4 个,合计面积2.86 hm2、蓄积量207 m3、林木资产9.04 万元;按村汇总得到全村杉木用材林面积89.96 hm2、蓄积量4 687 m3、林木资产188.03 万元。在评估有效期内,评估结果可以作为确定农户林权抵押贷款金额的参考依据。
3.2.4 评估模型检验与模型评价结果本研究以反映林分价值生长规律的序列林价理论为基础,通过调查森林经营过程、林业生产过程的技术经济指标,结合递推算法、模拟方法、回归估计技术,构建了系统性、结构化的小班林木资源资产评估模型。建模方法体现林分动态生长特点和森林经营生产实际,摆脱了单纯依赖大容量样本进行建模的困境,但模型的使用效果必须依靠市场交易实例样本作出统计检验和评价。
调查采集了98 个正常交易实例样本,应用小班林木资产评估模型对样本单元林木资产作出评估,得到各个样本单元成对的林木资产估算值、林木资产交易实际值,然后计算检验指标,对评估模型作出综合评价。F检验统计量F=1.782<F0.05(2,96)=3.094,说明在危险率5%条件下,小班林木资产的评估估算值与交易实际值之间差异不显著,评估模型是适用的。总相对误差-0.16%、平均相对误差1.25%、平均相对误差绝对值8.97%,估计精度97.6%(可靠性95%),说明小班林木资产评估模型不存在系统偏差,模型使用精度较高。
4 结论1 )集成运用了生产函数理论和建模技术,利用多源数据,研建了基于序列林价理论的林木资源资产评估模型,包括林分生长收获模型、序列林价递推模型、林价主要影响因素调整系数模型等,小班林木资产评估模型系统性、结构化,直观、可理解。经市场交易实例样本检验,所建的评估模型适用并且评估精度较高、评估效果较好。
2 )参照林分序列林价是小班林木资产评估中的参照物。序列林价表达了林价随林分年龄增大的变化规律,本文引入生产函数理论,有利于保证参照林分营林过程中投入与产出的匹配性。
3 )本文设计了序列林价递推算法,从造林开始至成熟林主伐年龄整个生长时期、投入(含林地地租)与产出一体化的序列林价推算,可以更好地研究序列林价。第一,避免“三段法”分时段造成完整生长过程的割裂,使序列林价全生长过程连续。第二,成本法递推算法、收益法递推算法实现了重置成本法、收益现值法、市场价倒算法3 种方法的融合与相互比较,使林木资产评估结果更具可靠性。价格的确定只能以交易双方可接受为标准(刘伟平,1995)。目前木材价格已经市场化,序列林价测算应当考虑供需双方意愿。成本途径反映供方价格水平,收益途径反映需方价格水平,同时采用2种途径计算序列林价,可以观察计算结果的合理性。第三,根据成本法递推算法、收益法递推算法2种方法计算结果综合确定参照林分序列林价时,成本法到收益法过渡段曲线容易识别,能够确定最佳修匀点,比“三段法”的曲线修匀做法更科学、更直观、更灵活。
4 )由于林龄价值系数具有相对的稳定性、通用性,所以通过参照林分成熟林主伐年龄时的林木资产评估值更新达到参照林分序列林价更新、小班林木资产评估模型更新。
5 )林价主要影响因素调整系数模型比较全面把握林分质量和林地质量、地利条件三方面状况对小班林木资产价值影响,并且建立了回归模型经验公式。把具体小班的集材路程和林分实物量因子代入公式即能直接快速计算小班林木资产价值。与目前仍惯用的、对林价主要影响因素作分级处理的分级价差评估方法比较,如分径级价差(苏宗海等,1992)、分区域价差、分交通距离等级价差、分龄组价差等,克服了自变量分级造成的林木价变化不连续和分级整化误差现象。
6 )基于序列林价的林木资产评估方法对森林资源资产抵押贷款、森林保险、林木资产核算等非交易性森林资源资产业务中的大批量小班林木资产评估工作具有适宜性,具有简便、快速、高效、低成本的评估操作特点。但序列林价评估方法有其局限性,转让、租赁等交易性森林资源资产业务往往有特殊情形,如交易双方特别约定的权益关系、特定的评估基准日等,不宜盲目应用序列林价评估方法。
| [1] |
胡敏荣, 孟全省. 2012. 多元回归分析法下森林资源资产批量评估模型研究——陕西省宁陕县实证案例. 林业经济 (8) : 61–65.
( Hu M R, Meng Q S.2012. Study on mass appraisal of forest resource assets based on multiple regression analysis-A case study on Ningshan County of Shaanxi Province. Forestry Economics (8) : 61–65. [in Chinese] ) (  0) 0)
|
| [2] | 井上は支えるから. 1984. 井上は支えるから. Beijing: China Forestry Publishing House : 78 -82. |
| [3] |
孔繁文, 王焕良, 刘东生. 1984. 论序列林价及其作用. 林业经济问题 (1) : 11–17.
( Kong F W, Wang H L, Liu D S.1984. Discussion on the sequential forest price and its function. Problems of Forestry Economic (1) : 11–17. [in Chinese] ) (  0) 0)
|
| [4] |
赖晓燕, 王霞. 2009. 基于多元回归分析的森林资源资产批量评估模型研究. 福建电脑 (11) : 94–95.
( Lai X Y, Wang X.2009. Study on the mass appraisal model of forest resources assets based on multiple regression analysis. Fujian Computer (11) : 94–95. [in Chinese] ) (  0) 0)
|
| [5] |
赖晓燕, 颜桂梅, 宁正元, 等. 2014. 2种森林资产批量评估模型的构建与比较. 福建农林大学学报:自然科学版 , 43 (1) : 39–43.
( Lai X Y, Yan G M, Ning Z Y, et al.2014. Modeling and comparison of two mass appraisal models of resources assets. Journal of Fujian Agriculture and Forestry University:Natural Science Edition , 43 (1) : 39–43. [in Chinese] ) (  0) 0)
|
| [6] |
廖克服, 廖世水, 李发沙. 1996. 三段式法序列林价表的编制. 福建林业科技 , 23 (3) : 54–56.
( Liao K F, Liao S S, Li F S.1996. Compilation of forest value list by using three stage method. Journal of Fujian Forestry Science and Technology , 23 (3) : 54–56. [in Chinese] ) (  0) 0)
|
| [7] |
廖士义, 李周, 徐智. 1983. 论林价的经济实质和人工林林价计量模型. 林业科学 , 19 (2) : 181–190.
( Liao S Y, Li Z, Xu Z.1983. Discussion on economic essence of forest price and the calculating model of man-made forest price. Scientia Silvae Sinicae , 19 (2) : 181–190. [in Chinese] ) (  0) 0)
|
| [8] |
刘伟平. 1995. 森林价格评估方法初探. 林业经济 (3) : 17–22.
( Liu W P.1995. Preliminary exploration on the evaluate of the price method in forest trade. Forestry Economic (3) : 17–22. [in Chinese] ) (  0) 0)
|
| [97] |
吕丹, 郑世跃, 欧阳勋志, 等. 2014. 基于BP神经网络的林木资源资产批量评估模型优化. 江西农业大学学报 , 36 (5) : 984–989.
( Lü D, Zheng S Y, OuYang X Z, et al.2014. Optimization of mass appraisal model for forest resource assets based on the BP neural network. Acta Agriculturae Universitatis Jiangxiensis , 36 (5) : 984–989. [in Chinese] ) (  0) 0)
|
| [10] |
马双柱, 王香明, 张拉锁, 等. 1989. 对用材林标准序列林价制定方法的研究. 林业经济 (3) : 48–61.
( Ma S Z, Wang X M, Zhang L S, et al.1989. Study on the compilation method of standard sequential forest price of timber forest. Forestry Economics (3) : 48–61. [in Chinese] ) (  0) 0)
|
| [11] |
施恭明, 李宝银, 洪端芳, 等. 2015. 福建省马尾松人工林二元立木材积方程检验与修订. 森林与环境学报 , 35 (1) : 81–86.
( Shi G M, Li B Y, Hong D F, et al.2015. Verification and revision of two-entry tree volume equation of Pinus massoniana plantation in Fujian Province. Journal of Forest and Environment , 35 (1) : 81–86. [in Chinese] ) (  0) 0)
|
| [12] |
苏宗海, 綦秀兰. 1992. 立木林价表的理论依据及其应用. 北京林业大学学报:社会科学版 (Suppl) : 65–73.
( Su Z H, Qi X L.1992. Theoretical basis and application of forest stumpage price list. Journal of Beijing Forestry University:Social Scienc (Suppl) : 65–73. [in Chinese] ) (  0) 0)
|
| [13] |
王兆君, 刘降斌. 2009. 基于回归分析的森林资源资产批量评估问题探究. 学术交流 (5) : 97–101.
( Wang Z J, Liu J B.2009. Study on the problem of mass appraisal of forest resources assets based on regression analysis. Academic Exchange (5) : 97–101. [in Chinese] ) (  0) 0)
|
| [14] |
吴承祯, 洪伟. 1995. 福建省杉木人工林序列林价及其应用研究. 福建林学院学报 , 15 (3) : 218–222.
( Wu C Z, Hong W.1995. Study on the forest value list of Chinese fir plantation in Fujian Province and its application. Journal of Fujian College of Forestry , 15 (3) : 218–222. [in Chinese] ) (  0) 0)
|
| [15] |
谢哲根, 韩国康, 汪永红, 等. 2012. 森林资源资产评估需求与行业发展建设. 世界林业研究 , 25 (5) : 5–10.
( Xie Z G, Han G K, Wang Y H, et al.2012. Demand and the industrial development establishment of forest resource assets assessment. World Forestry Research , 25 (5) : 5–10. [in Chinese] ) (  0) 0)
|
| [16] |
谢哲根, 何必庭, 童红卫, 等. 2014. 基于林分水平的森林资源资产价值组成研究. 北京林业大学学报:社会科学版 , 13 (4) : 61–66.
( Xie Z G, He B T, Tong H W.2014. A research on the composition of forest resources assets value based on stand level.. Journal of Beijing Forestry University:Social Sciences , 13 (4) : 61–66. [in Chinese] ) (  0) 0)
|
| [17] |
尹惠妍, 李海奎. 2014. 基于蓄积的森林生物量估算方法的对比分析. 林业科学研究 , 27 (6) : 848–853.
( Yin H Y, Li H K.2014. Comparison of the methods estimating forest biomass based on stock volume. Forest Research , 27 (6) : 848–853. [in Chinese] ) (  0) 0)
|
| [18] |
臧斌, 王友玉, 杨造林, 等. 1991. 马尾松人工林序列林价调查浅析. 江苏林业科技 (4) : 23–28.
( Zang B, Wang Y Y, Yang Z L, et al.1991. Shallow analysis on the sequential forest price of the artificial forest of Masson pine. Journal of Jiangsu Forestry Science & Technology (4) : 23–28. [in Chinese] ) (  0) 0)
|
| [19] |
张和根. 1988. 福建省杉木、马尾松人工林序列林价表调制的研究. 福建林学院学报 , 8 (3) : 258–265.
( Zhang H G.1988. Study on the modulation in forest value list of Chinese fir and Masson pine plantations in Fujian. Journal of Fujian College of Forestry , 8 (3) : 258–265. [in Chinese] ) (  0) 0)
|
| [20] |
张汝淼, 郭志琦. 1988. 对《标准序列林价表的制定及其应用》一文的几点商榷. 山西林业科技 (3) : 28–30.
( Zhang R M, Guo Z Q.1988. Some discussions on the article of 《compilation and application of standard sequential forest price》. Shanxi Forestry Science and Technology (3) : 28–30. [in Chinese] ) (  0) 0)
|
| [21] |
张树青, 陆加胜. 1990. 实用序列林价计算方法的研究. 吉林林业科技 (5) : 50–54.
( Zhang S Q, Lu J S.1990. Study on the calculation method of practical sequential forest price. Journal of Jilin Forestry Science and Technology (5) : 50–54. [in Chinese] ) (  0) 0)
|
| [22] |
郑德祥, 赖晓燕, 陈平留. 2012. 基于多元线性回归的森林资源资产批量评估研究. 中国资产评估 (2) : 30–35.
( Zheng D X, Lai X Y, Chen P L.2012. Study on mass appraisal of forest resources assets based on multiple linear regression. Appraisal Journal of China (2) : 30–35. [in Chinese] ) (  0) 0)
|
| [23] |
郑德祥, 赖晓燕, 廖晓丽. 2013. 基于贝叶斯正则化BP神经网络的森林资源资产批量评估研究. 福建林学院学报 , 33 (2) : 132–136.
( Zheng D X, Lai X Y, Liao X L.2013. Study on the mass appraisal of forest resources assets based on Bayesian regularization BP neural network. Journal of Fujian College of Forestry , 33 (2) : 132–136. [in Chinese] ) (  0) 0)
|
| [24] |
曾林. 1995. 人工用材林林价的测算. 林业资源管理 (3) : 39–73.
( Zeng L.1995. Calculation of artificial timber forest price. Forestry Resources Management (3) : 39–73. [in Chinese] ) (  0) 0)
|
| [25] |
曾伟生, 唐守正. 2011. 立木生物量方程的优度评价和精度分析. 林业科学 , 47 (11) : 106–113.
( Zeng W S, Tang S Z.2011. Goodness evaluation and precision analysis of tree biomass equations. Scientia Silvae Sinicae , 47 (11) : 106–113. [in Chinese] ) (  0) 0)
|
| [26] | Liu X B. 2012. Research on model structuring mass appraisal of regression analysis-based forest reserves assets//IEEE Computer Society. ICEE'12 Proceedings of the 20123rd International Conference on E-Business and E-Government:Volume 2. Washington:IEEE Computer Society 913-916. |
| [27] | Wagniere S. 2011. Forest valuation:a knowledge-based view. Doctoral dissertation, University of St. Gallen, Switzerland. |
 2016, Vol. 52
2016, Vol. 52

