文章信息
- 马岩, 许洪刚, 杨春梅, 许世祥
- Ma Yan, Xu Honggang, Yang Chunmei, Xu Shixiang
- 小径木星形纵向锯解后重组刨切单板的数学理论描述
- Description of Small-Diameter Wood Sliced Veneer after Star-Sawing in Longitudinal Direction and Recombining by Mathematical Method
- 林业科学, 2016, 52(12): 106-111
- Scientia Silvae Sinicae, 2016, 52(12): 106-111.
- DOI: 10.11707/j.1001-7488.20161213
-
文章历史
- 收稿日期:2015-12-01
- 修回日期:2016-01-08
-
作者相关文章
刨切单板重组木是在不打乱木材纤维排列方向、保留木材基本特性的前提下,将小径级原木疏解成平整单板,再经干燥、铺装、施胶和热压(或模压)等重新组合工序制成的高强度、大规模、具有天然木材纹理结构的新型木材(李伟光等,2008; 于文吉,2012; 2013)。我国小径级原木产地较多,但小径木应用较单一,且出材率较低,限制了小径木的大规模生产; 而新型星形下锯法能够以高效率的方式更好地利用小径级原木(任洪娥,2001)。本文对原木及星形下锯刨切后得到的弦切单板进行数学建模,并以此为基础实现刨切下锯的优化设计,以期提高原木出材率。
1 星形纵向锯解后重组刨切单板工艺星形纵向锯解后重组刨切纹理板是将小径木纵向锯解为多块扇形木材后重组为近似板材再刨切为弦切单板的工艺。星形下锯法制造的锯材在硬度、表面精度、观赏性等方面具有突出的优点(贾满蓉等,1992; 朱国玺等,1994),其下锯图见图 1。

|
图 1 星形下锯工艺下锯 Fig.1 The star-sawing technology sawing pattern δ1: 弦切单板板面与该板和年轮切线的夹角 The angle between the face cut board and its tangent with annual ring; β: 扇形板材的角度 The angle of sector board. |
扇形板材重新组合为近似板材后再进行刨切得到弦切单板,将弦切单板拼凑使用(图 2),其纹理美观大方、自然典雅,且硬度及表面精度高,具有很高的经济价值(马岩等,1995; 张少纯等,1997)。板面与该板和年轮切线的夹角δ1在航空、乐器制造等不同领域要求不同,所以星形下锯每块扇形板材的角度β取决于δ1。对不同角度其研究方法基本相同,本文只讨论β=90°的情况(陈桂华,2003; 马岩,2005)。
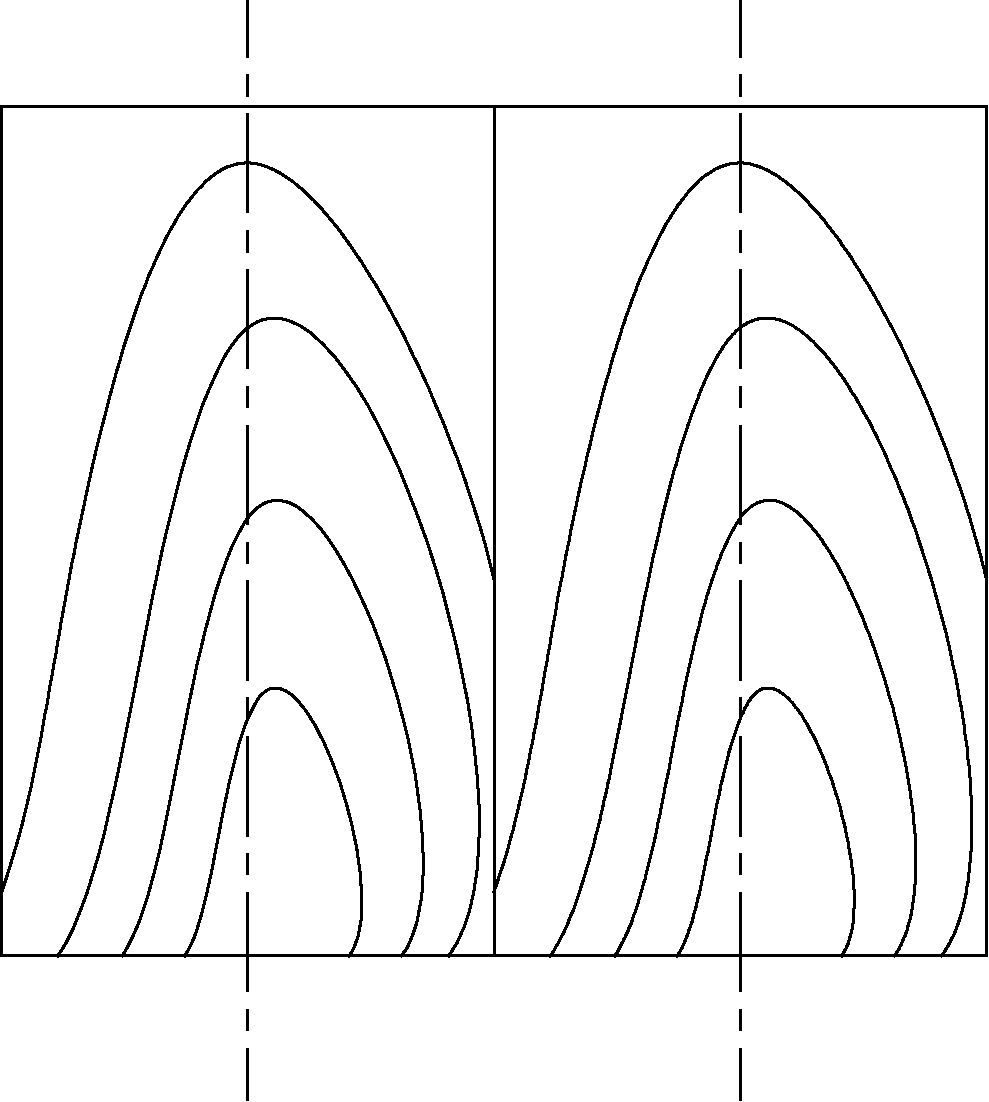
|
图 2 弦切单板 Fig.2 The face cut board |
随着科技不断创新,在木材加工领域,制材工艺也在迅速革新发展,计算机辅助设计、制材下锯优化已经在木材加工中开始使用。传统原木出材率的优化主要是将原木加工成矩形大板(马岩等,1995),锯切后废材较多,而星形纵向锯解后重组刨切单板的优化则没有这个缺陷,具有很高的发掘潜力(童雀菊,1996; Sandberg et al.,1997)。但要找到最优解,必须建立原木及星形下锯刨切得到弦切单板的数学模型,才能通过计算机求出最优下锯尺寸,作为星形下锯及刨切下刀的理论基础。
2.1 刨切弦切单板的原木数学模型刨切弦切单板的描述体系以理想原木(图 3)为基础,原木截顶面数学模型为椭圆幂曲线。取原木的小头长径Da1、小头短径Db1、中央断面短径Dbm、大头长径Da2和材长L为实测值,则理想原木的数学模型(马岩,1990; 冯莉,2002)为:
| $F\left( {x,y,z} \right) = \left\{ {\begin{array}{*{20}{l}} {\frac{{4D_{a1}^2{L^t}}}{{D_{b1}^2D_{a2}^2 - D_{a1}^2}}{x^2} + \frac{{4{L^t}}}{{D_{a2}^2 - D_{a1}^2}}{y^2} \le \frac{{D_{a2}^2}}{4} - {z^t};}\\ {0 \le z \le L;}\\ {\frac{{4D_{a1}^2{L^t}}}{{D_{b1}^2D_{a2}^2 - D_{a1}^2}}\frac{{4{L^t}}}{{D_{a2}^2 - D_{a1}^2}} \ge 0} \end{array}} \right.F\left( {x,y,z} \right) = \left\{ {\begin{array}{*{20}{l}} {\frac{{4D_{a1}^2{L^t}}}{{D_{b1}^2D_{a2}^2 - D_{a1}^2}}{x^2} + \frac{{4{L^t}}}{{D_{a2}^2 - D_{a1}^2}}{y^2} \le \frac{{D_{a2}^2}}{4} - {z^t};}\\ {0 \le z \le L;}\\ {\frac{{4D_{a1}^2{L^t}}}{{D_{b1}^2D_{a2}^2 - D_{a1}^2}}\frac{{4{L^t}}}{{D_{a2}^2 - D_{a1}^2}} \ge 0.} \end{array}} \right.$ | (1) |
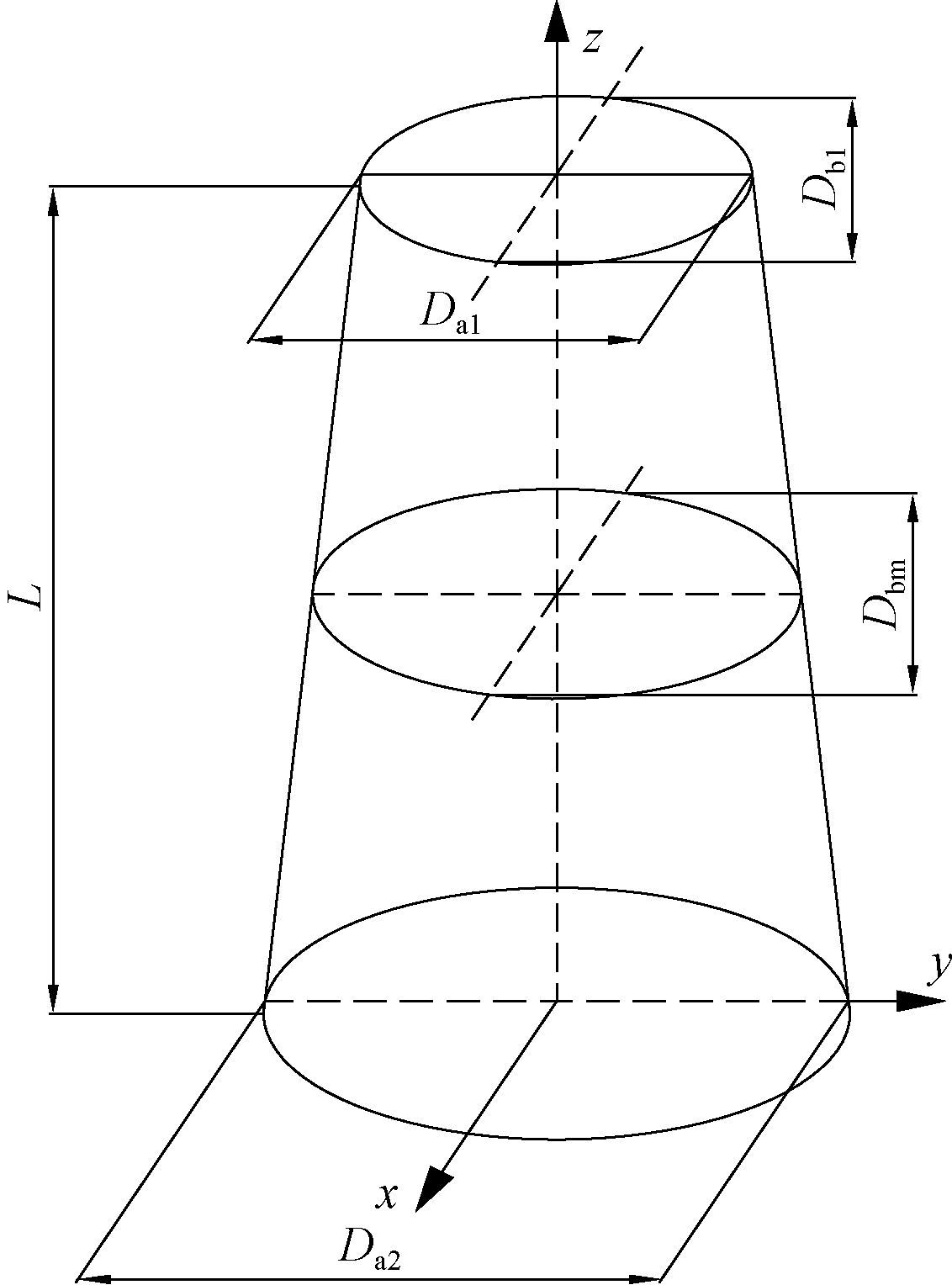
|
图 3 理想原木的数学模型 Fig.3 The ideal mathematical model of log |
式(1)椭圆幂函数柱体的顶点沿着z向平移,随着幂次的变化,幂曲面的凸凹程度可以模拟原木干曲线的不同形状。而式中t的确定是将实测的具体点(Dbm/2,0,L/2)代入式(1)中求出来的,t可以控制树干纵断面曲线的凸凹程度,将实测点带入计算后,得到其公式如下:
| $\begin{array}{l} t = 1.442{\rm{ }}7[\frac{{D_{b1}^2\left( {D_{a2}^2 - 1} \right) + D_{a1}^2\left( {D_{bm}^2 - D_{b1}^2} \right)}}{{D_{b1}^2 - D_{bm}^2D_{a1}^2}} - \\ {\left( {\frac{{D_{b1}^2\left( {D_{a2}^2 - 1} \right) + D_{a1}^2\left( {D_{bm}^2 - D_{b1}^2} \right)}}{{D_{b1}^2 - D_{bm}^2D_{a1}^2}}} \right)^2}/2]. \end{array}$ | (2) |
从大量统计分析可知,原木截面大约60%为椭圆(包括近似多边形、蛋圆); 而对原木干曲线的分析可知,其干曲线有可能为抛物线、直线等,在一定区间内都可以看作是连续幂曲线。因此,大多数原木可以视为截面为椭圆、椭圆度数为常数、树干中心线为直线、纵断面边界曲线为连续的幂曲线,但是在实际问题处理中需要针对不同问题进行具体处理。
2.2 短径方向弦切单板的数学模型图 4为星形下锯所得扇形木材刨切为弦切单板在原木中的示意图。星形纵向锯解后重组刨切纹理板是将小径木纵向锯解为多块扇形木材后按图 5所示方式重组为近似板材,再按图 5中v所示方向进行纵向刨切为弦切单板的工艺。为了寻找对近似板材刨切时最优下刀,提高出材率,需对近似板材中弦切单板进行数学建模(只需对其中1块扇形板材中的弦切单板建模即可)。

|
图 4 长短径方向弦切单板 Fig.4 The face cut board of long and short trail direction Ⅰ.垂直于短径方向纵向刨切所得弦切单板The face cut board of longitudinal slicing perpendicular to the short direction; Ⅱ.垂直于长径方向纵向刨切所得弦切单板The face cut board of longitudinal slicing perpendicular to the long trail direction. |

|
图 5 短径方向弦切单板的数学模型 Fig.5 The mathematical model of face cut board’s short trail direction |
讨论以图 4中Ⅰ所示即短径方向弦切单板为模型进行最优下刀时的情况。根据图 5可以得到短径方向弦切单板的数学模型(齐英杰等,2008)为:
| $\left\{ \begin{array}{l} F\left( {x,y,z} \right) \ge 0;\left( 3 \right)\\ {H_0} \ge x + {D_{a1}}/2 - {S_0} \ge 0;\left( 4 \right)\\ S \ge S + y - \left( {{D_{b1}}/2 - {S_0}} \right) \ge 0;\left( 5 \right)\\ \frac{{D_{a2}^2}}{4} - {z^t}_1 - \frac{{4D_{a1}^2{L^t}}}{{D_{b1}^2\left( {D_{a2}^2 - D_{a1}^2} \right)}}{x^2} - \frac{{4{L^t}}}{{D_{a2}^2 - D_{a1}^2}}{y^2} \ge 0;{\rm{ }}\left( 6 \right)\\ 2{D_{a1}}\left( {{D_{b1}}/2 - {S_0} - S} \right) - {D_{b1}}H = 0;\left( 7 \right)\\ 0 \le {z_1} \le L.\left( 8 \right) \end{array} \right.$ |
式中: S0为单板厚度方向定位尺寸; S为单板厚度; H0为短径方向弦切单板宽度。
F(x,y,z)是理想原木数学模型,式(4)限制了其x向的定义域,并且保证了弦切单板对称于y轴,式(6)保证了弦切单板所有点都位于原木模型内,式(7)则是对弦切单板板面与该板年轮切线夹角δ1的限定,因为本文讨论β=90°的情况,所以得出该式,若讨论其他情况时可参照式(9)具体分析:
| $\beta /2 \le arctan\left[ {\frac{{{D_{a1}}tan{\delta _1}}}{{{D_{b1}}}}} \right].$ | (9) |
在讨论以图 4中Ⅱ所示即长径方向弦切单板为模型进行最优下刀的情况时,根据类比方法求解,只是将建模的图 4中Ⅰ所示短径方向扇形板材变为图 4中Ⅱ所示长径方向扇形板材,故长径方向模型不再赘述。同理,在限定δ1时参照式(10):
| $\beta /2 \le arctan\left[ {\frac{{{D_{b1}}tan{\delta _1}}}{{{D_{a1}}}}} \right].$ | (10) |
长径方向弦切单板的数学模型为:
| $\left\{ \begin{array}{l} F\left( {x,y,z} \right) \ge 0;\left( {11} \right)\\ {H_1} \ge x + {D_{b1}}/2 - {S_0} \ge 0;\left( {12} \right)\\ S \ge S + y - \left( {{D_{a1}}/2 - {S_0}} \right) \ge 0;\left( {13} \right)\\ \frac{{D_{a2}^2}}{4} - z_1^t - \frac{{4D_{a1}^2{L^t}}}{{D_{b1}^2\left( {D_{a2}^2 - D_{a1}^2} \right)}}{x^2} - \frac{{4{L^t}}}{{D_{a2}^2 - {D^2}_{a1}}}{y^2} \ge 0;\left( {14} \right)\\ 2{D_{b1}}\left( {{D_{a1}}/2 - {S_0} - S} \right) - {D_{a1}}H = 0;\left( {15} \right)\\ 0 \le {z_1} \le L.\left( {16} \right) \end{array} \right.$ |
式中: H1为长径方向弦切单板宽度。
每个方程的含义与短径方向相类似。通过对比式(4)与式(12)可以明显看出H0>H1,即短径方向弦切单板宽度大于长径方向弦切单板宽度。故要求弦切单板宽度时,应以短径方向弦切单板为模型基础进行最优下刀;要求弦切单板数量时,应以长径方向弦切单板为模型基础进行最优下刀。
3 星形下锯和直接刨切出材率计算 3.1 星形纵向锯解后重组刨切单板出材率计算在计算出材率时,合格单板的体积计算过程复杂,难度较大,所以需要先计算废料体积,然后计算得出合格单板体积。由星形纵向锯解后重组刨切单板工艺可知,需要丢弃的第1部分为第1次从原木上刨切下的板皮; 第2部分为扇形板材刨切剩余的中间芯材,具体为一个底边为20 mm、高为10 mm的等边三角形。如图 6所示阴影部分即为需要丢弃的废料,出材率具体计算公式(周亚光等,1992)如下:
| $扇形板材刨切弦切单板出材率 = \frac{{扇形板材材积 - 废料体积}}{扇形板材材积}.$ | (17) |
因计算体积时高度是相同的,故只需计算各截面积即可。设S0为扇形板材截面积,S1为板皮的面积,S2为剩余芯材的面积,如图 6中对拼板截面进行y向积分,得到式(18):
| $\begin{array}{l} \frac{{{D_{a1}}{D_{b1}}}}{{\sqrt {4D_{a1}^2 + 4D_{b1}^2} }}\\ {S_0} = \smallint \sqrt {\frac{{D_{b1}^2}}{4}\left( {1 - \frac{{4{y^2}}}{{D_{a1}^2}}} \right)} dy - {\rm{ }}\frac{{D_{a1}^2D_{b1}^2}}{{4D_{a1}^2 + 4D_{b1}^2}}.\\ \frac{{ - {D_{a1}}{D_{b1}}}}{{\sqrt {4D_{a1}^2 + 4D_{b1}^2} }} \end{array}$ | (18) |

|
图 6 扇形板材刨切横截面 Fig.6 The sliced cross section of fan shapes board |
对式(18)求解得到:
| $\begin{array}{l} {S_0} = \frac{{{D_{a1}}{D_{b1}}}}{2}(\left( {\frac{1}{2}{\alpha _x} + {C_0}} \right)\left| {\begin{array}{*{20}{c}} {arcsin\frac{{2{D_{b1}}}}{{\sqrt {4D_{a1}^2 + 4D_{b1}^2} }}}\\ 0 \end{array}} \right. + \\ \frac{1}{4}sin2{\alpha _x}\left| {\begin{array}{*{20}{c}} {arcsin\frac{{2{D_{b1}}}}{{\sqrt {4D_{a1}^2 + 4D_{b1}^2} }}}\\ 0 \end{array}} \right. - \frac{{D_{a1}^2D_{b1}^2}}{{4D_{a1}^2 + 4D_{b1}^2}}. \end{array}$ | (19) |
式中:
| $sin{\alpha _x} = 2y/{D_{a1}}.$ | (20) |
同理,对板皮截面部分x向进行积分,得式(21):
| ${S_1} = 2\int_{\frac{{{D_{b1}}}}{2} - 2}^{\frac{{{D_{b1}}}}{2}} {} \sqrt {\frac{{D_{a1}^2}}{4}\left( {1 - \frac{{4{x^2}}}{{D_{b1}^2}}} \right)} dx.$ | (21) |
对式(21)求解得到:
| $\begin{array}{l} {S_1} = \frac{{{D_{a1}}{D_{b1}}}}{2}(\left( {\frac{1}{2}{\alpha _x} + {C_0}} \right)\left| {\begin{array}{*{20}{c}} {\frac{\pi }{2}}\\ {arcsin1 - \frac{4}{{{D_{b1}}}}} \end{array}} \right. + \\ \left( {\frac{1}{4}sin2{\alpha _x}} \right)\left| {\begin{array}{*{20}{c}} {\frac{\pi }{2}}\\ {arcsin1 - \frac{4}{{{D_{b1}}}}} \end{array}} \right.). \end{array}$ | (22) |
由图 6很容易得到剩余芯材截面积为:
| ${S_2} = 20 \times 10 \times 0.5 = 100(m{m^2})$ | (23) |
出材率具体计算公式如式(24),将式(18)、式(21)、式(23)分别带入式(24)即可计算出出材率:
| $\eta = {S_0} - {S_1} - {S_2}{S_0} \times 100\% .$ | (24) |
利用式(24)可以实现对原木星形纵向锯解后重组刨切单板进行近似出材率的计算。通过实际测量4组典型原木长径及短径参数,分别代入出材率计算公式,得到原木刨切单板出材率如表 1所示。但需要注意的是,计算结果是在理想原木情况下得到的,只是为了验证星形下锯可以提高小径木出材率; 在实际计算中,还应对木材的弯曲度和节子、虫眼等缺陷进行不同的讨论(Castellani et al.,2009)。
|
|
直接刨切小径木出材率参照星形纵向锯解后重组刨切单板出材率计算,计算公式如下:
| $直接刨切小径木出材率 = \frac{{小径木材积 - 料体积}}{小径木材积}.$ | (25) |
同样转换为截面积计算如图 7所示,需要丢弃第1部分为第1次从小径木刨切下的板皮; 第2部分为小径木直接刨切剩余的中间芯材,其具体尺寸为Da1(Db1)×20 mm的近似矩形板材。由图 7可以看出,两侧弧顶面积所占中间剩余板材比例非常小,可以忽略不计,计算时剩余中间芯材可按照矩形计算。设S0为小径木总截面积,S1为板皮的面积,S2-1为垂直于短径方向刨切剩余芯材的面积,S2-2为垂直于长径方向刨切剩余芯材的面积,η1为垂直于短径方向刨切出材率,η2为垂直于长径方向刨切出材率,由图 7可得:
| ${S_0} = \pi /4 \times {D_{a1}} \times {D_{b1}};$ | (26) |
| ${S_2} = {D_{a1}}({D_{b1}}) \times 20.$ | (27) |

|
图 7 小径木直接刨切横截面 Fig.7 The sliced cross section of small-diameter |
S1板皮部分的面积同星形下锯板皮计算,出材率计算同式(24),将实测数值带入得表 2。
|
|
对比表 1与表 2可以明显得到,星形纵向锯解后重组刨切单板的工艺较直接刨切小径木可以提高小径木出材率; 而且随着小径木尺寸的增大,其出材率也相应提高(马玉英,2003; Sillett et al.,2009)。
4 结论以建立的原木及弦切单板数学模型为基础,完全能够建立原木最优星形下锯图及最优刨切图,从而能够提高原木出材率。 通过对模型的比较,短径方向弦切单板宽度大于长径方向弦切单板宽度,要求弦切单板宽度时,应以短径方向弦切单板为模型基础进行最优下刀;要求弦切单板数量时,应以长径方向弦切单板为模型基础进行最优下刀。 通过实际测量几组典型原木参数,并分别对小径木采用星形纵向锯解后重组刨切单板与直接刨切2种工艺进行出材率计算,结果显示,采用星形纵向锯解后重组刨切单板的工艺提高了小径木出材率,且随着小径木尺寸的增大,其出材率也相应提高,这也为实际选材提供了依据。
| [] | 陈桂华. 2003. 单板旋切过程中后角变化的理论分析. 林业机械与木工设备 , 31 (10) : 10–12. |
| [] | Chen G H.2003. Theory analysis of change of peeling clearance angle. Forestry Machinery & Woodworking Equipment , 31 (10) : 10–12. |
| [] | 冯莉. 2002. 原木材积计算机视觉检测系统的研究. 哈尔滨:东北林业大学硕士学位论文. http://cdmd.cnki.com.cn/Article/CDMD-10225-2002121891.htm |
| [] | Feng L. 2002. Research on log volume measuring system by computer vision. Harbin:MS thesis of Northeast Forestry University. [in Chinese] |
| [] | 贾满蓉, 张美筠, 庞东芬. 1992. 辐射下锯法拓宽了小径原木的利用途径. 国外林业 (3) : 42–43. |
| [] | Jia M R, Zhang M J, Pang D F.1992. The use of small-diameter has been widened by radiation sawing method. Foreign Forestry (3) : 42–43. |
| [] | 李伟光, 郭晓磊, 曹平祥. 2008. 单板刨切技术的现状与发展. 木材加工机械 (6) : 37–39. |
| [] | Li W G, Guo X L, Cao P X.2008. The discussion on the technology of veneer slicing. Wood Processing Machinery (6) : 37–39. |
| [] | 马岩. 1990. 理想原木材积通式和缺陷原木模型与材积推导. 东北林业大学学报 , 18 (4) : 81–94. |
| [] | Ma Y.1990. Common scale formulation of ideal log and model and scale detecting fault log research. Journal of Northeast Forestry University , 18 (4) : 81–94. |
| [] | 马岩, 齐玉成, 关小平, 等. 1995. 原木削片制大方材下锯图优化研究. 木材加工机械 (1) : 8–9. |
| [] | Ma Y, Qi Y C, Guan X P, et al.1995. Study on the optimization of sawing pattern in in log slices to lumber. Wood Processing Machinery (1) : 8–9. |
| [] | 马岩. 2005. 利用板材端面纹理判断和识别板材几何参数的数学描述理论. 生物数学学报 , 20 (2) : 245–250. |
| [] | Ma Y.2005. Mathematical description research on judging and distinguishing parameter of plank by vein of section. Journal of Biomathematics , 20 (2) : 245–250. |
| [] | 马玉英. 2003. 提高原木出材率的工艺措施. 林业科技 , 28 (3) : 44–45. |
| [] | Ma Y Y.2003. The technical measures to improve the rate of volume ratio. Forestry Science and Technology , 28 (3) : 44–45. |
| [] | 齐英杰, 马岩. 2008. 原木裁板皮过程的建模理论与仿真方法. 林业科学 , 44 (12) : 112–115. |
| [] | Qi Y J, Ma Y.2008. Modeling theory and simulation method of logs being cut out board paper process. Scientia Silvae Sinicae , 44 (12) : 112–115. |
| [] | 任洪娥. 2001. 新型星形下锯法第一道工序加工过程的数学描述. 东北林业大学学报 , 29 (1) : 76–78. |
| [] | Ren H E.2001. The description of the first sawing process for the new star-sawing pattern by mathematical method. Journal of Northeast Forestry University , 29 (1) : 76–78. |
| [] | 童雀菊. 1996. 几种径向下锯模型的比较. 南京林业大学学报 , 20 (2) : 54–59. |
| [] | Tong Q J.1996. Comparative analysison various radial sawing patterns. Journa of Nanjing Forestry University , 20 (2) : 54–59. |
| [] | 于文吉. 2012. 我国重组竹产业发展现状及趋势分析. 木材工业 , 26 (1) : 11–14. |
| [] | Yu W J.2012. Current status and future development of bamboo scrimber industry in China. China Wood Industry , 26 (1) : 11–14. |
| [] | 于文吉. 2013. 我国木、竹重组材产业发展的现状与前景. 木材工业 , 27 (1) : 5–8. |
| [] | Yu W J.2013. Development and prospect of wood and bamboo scrimber industry in China. China Wood Industry , 27 (1) : 5–8. |
| [] | 张少纯, 朱孝生, 巴兴强, 等. 1997. 单板旋切厚度均匀性分析及改进措施. 东北林业大学学报 , 25 (2) : 75–77. |
| [] | Zhang S C, Zhu X S, Ba X Q, et al.1997. Analysis of the evenness of venner peeling thickness and improving measures. Journal of Northeast Forestry University , 25 (2) : 75–77. |
| [] | 周亚光, 诸燕子. 1992. 梯形下锯法与其它下锯法的出材率. 国外林业 (1) : 29–32. |
| [] | Zhou Y G, Zhu Y Z.1992. The volume ratio of trapezoidal sawing and other sawing methods. Foreign Forestry : 29–32. |
| [] | 朱国玺, 马岩, 卢军, 等. 1994. 短周期工业用材多锯片剖分过程的数学模拟研究. 林业科学 , 30 (6) : 556–561. |
| [] | Zhu G X, Ma Y, Lu J, et al.1994. The mathematical simulate research of the short felling cyclepole-timbers on sawing were ripped by slasher saw. Scientia Silvae Sinicae , 30 (6) : 556–561. |
| [] | Castellani M, Rowlands H.2009. Evolutionary artificial neural network design and training for wood veneer classification. Engineering Applications of Artificial Intelligence , 22 (4/5) : 732–741. |
| [] | Sandberg D, Wålinder M, Wiklund M. 1997. The concept of value activation:a better utilization of wood. Stockholm:KTH Royal Institute of Technology, 13. |
| [] | Sillett S C, Van Pelt R, Koch G W, et al.2009. Increasing wood production through old age in tall trees. Forest Ecology and Management , 259 (5) : 976–994. |
 2016, Vol. 52
2016, Vol. 52

