文章信息
- 马岩, 许洪刚, 杨春梅, 许世祥
- Ma Yan, Xu Honggang, Yang Chunmei, Xu Shixiang
- 小径木双面刨切单板的材积计算与效益分析
- Volume Calculation Method and Benefit Analysis of Small-Diameter Wood Sided Sliced Veneer
- 林业科学, 2016, 52(11): 142-147
- Scientia Silvae Sinicae, 2016, 52(11): 142-147.
- DOI: 10.11707/j.1001-7488.20161117
-
文章历史
- 收稿日期:2015-12-01
- 修回日期:2016-01-18
-
作者相关文章
我国经济持续、快速和稳定的发展,拉动了对木材的需求,而我国森林资源匮乏,可供木材严重不足,尤其是1998年实施天然林保护工程后,更加剧了木材供应的紧张程度(王宏棣,2007;刘玉善,2012)。在这种情况下,小径木逐渐引起了人们的注意,但由于小径木自身物理性质影响,其所加工的产品易发生开裂、弯曲变形等缺陷。为了解决此问题,有学者提出将小径木分解为单板,然后再将分解后的单板重新组合为重组木的方案(于文吉,2013;余养伦等,2013),重组木的性能非常优异,其强度、纹理等与实木相比不相上下,甚至优于实木(李伟光,2008;王晓欢等,2009)。但传统制备重组木木束很多关键环节加工不够精确,导致产品出现翘曲、表面不光整等现象,而且其加工效率以及出材率都很低,很难形成产业化(王晓欢等,2009;马岩,2011),大大降低了其经济效益。要制备符合要求的合格重组木,就需要制备合格的单板(Jin, 2001),因此精确计算出单板的材积及出材率,并以此为依据进行小径木合理选材和精确下刀刨切,对制备合格重组木非常重要。
1 双面刨切工艺双面刨切是指从小径木两侧同时对小径木进行纵向刨切。开始加工之前,调整两侧刨刀的初始位置,精确找正对刀,调整结束后刨刀进行纵向进给刨切,刨切时前刀面带来的剪切应力不断挤压小径木两侧的木材,造成切削木材的弯曲及剪切,在刀刃口前会形成超前的细小缝隙,当两侧切削木材受到的剪切应力达到临界值时,切削木材就会发生变形(Sheikh-Ahmod et al., 1999; 孙义刚等,2010)。随着刨刀的不断纵向进给,切削刃前未变形的木材不断受到切削刃带来应力的挤压,切削木材连续发生变形(周兰美等,2004;Aguilera et al., 2007),这样每次刨切结束可以同时制备2块光滑的单板(Olufemi, 2012)。一次刨切结束后,刨刀返回工作初始位置,两侧刨刀同时横向进给2 mm,进行下一次刨切,如此循环,直至小径木剩余厚度为20 mm的固定芯板时结束刨切。
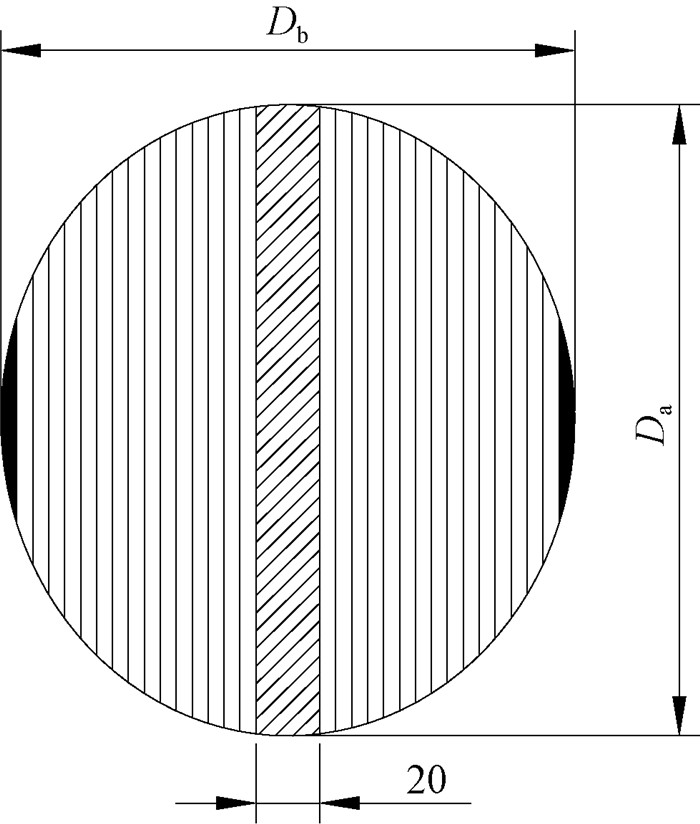
1.1 刨切下刀图双面刨切小径木下刀如图 1所示。
|
图 1 双面刨切下刀 Fig.1 The sides slicing's cutting feed |
本文所讨论小径木假定为没有缺陷、纵截面是幂曲线、横截面是椭圆的理想小径木。如图 1所示,Da为横截面椭圆长径,Db为横截面椭圆短径。第1次进给刨切制备的单板称作板皮,不能加工成为完整的单板,所以刨切完的两侧板皮是需要丢弃的废弃料。图中阴影部分为单板板皮截面。按照图示实线进行下刀进给,每次刨切都可以同时制备2块等厚且光整的单板,经过多次循环刨切后,剩余中间部分厚度为20 mm的固定芯板,刨切结束后取下剩余的固定芯板等待下一工序的加工。
1.2 双面纵向刨切的优点双面刨切同时对小径木相对的2个平面进行纵向刨切,可以同时获得等厚且光整的单板,而且每次刨切结束后剩余的固定芯板需要重新叠加起来,并且沿着垂直于固定芯材两侧刨切面方向再次进行刨切。所以双面刨切较其他刨切方式具有以下明显优点(刘孝岷,2008):
1) 双面刨切可连续生产,同时对小径木相对的2个平面进行刨切,提高了机械化和自动化程度,小径木只需1次装夹即可完成整体的刨切,节省了反复装卡木材的时间,节省了人力物力,大大提高了生产效率(马岩,2006)。
2) 因为每次刨切结束后剩余的固定芯板需要进行再次刨切,每次完整加工剩余的废料仅为两侧板皮以及中间20 mm×20 mm的固定芯材,所以大大提高了小径木的出材率,从而提高了经济效益。
3) 因为每次刨切的方向都是顺着小径木的纤维方向进行的,相对于垂直木纤维方向的刨切,所需剪切应力小,而且不会造成横向刨切时产生的单板裂纹。双面纵向刨切时噪声小,工作平稳,安装调试容易。
1.3 中间固定芯板的处理工艺对于刨切加工结束后剩余的固定芯板,除了中间木髓部分不能制备重组木外,其他部分都可以作为制备重组木的合格材料,如果将其直接作为废弃料丢弃,则降低了小径木的出材率。针对这个问题,将加工后剩余的中间固定芯板按图 2所示叠加起来,并在剩余芯材后侧用限位块1进行限位,从上侧方向用夹紧钉进行施力夹紧,使叠加夹紧后的芯材端面与刨刀刀刃方向和刨切运动方向都垂直,然后沿着垂直于固定芯材两侧刨切面方向进行纵向循环刨切。具体如图 2所示,箭头v方向为刀具进给方向,中间阴影为剩余废弃芯材,细实线为下刀位置。

|
图 2 固定芯板双面刨切 Fig.2 The fixed cores' sides slicing 1.限位块Limit block;2.夹紧钉Clamping nail;3.刨刀Planer. |
经过双面刨切加工后的小径木剩余部分仅为中间20 mm×20 mm的芯材和两侧板皮,所以小径木经过第1次双面刨切及第2次中间固定芯板刨切后,丢弃的废料减少,而得到制备合格重组木的单板数量增加(刘玉娟等,2011)。
2 双面刨切单板的材积计算为保证刨切单板的精确下刀,提高小径木出材率,需要对小径木材积进行计算。以短径方向单板为例(图 3),Da1为小径木小头横截面椭圆短径,Db1为其长径,Da2为小径木大头横截面椭圆短径,Db2为其长径,其数学模型(马岩,1990;陆贵添,2012)为:
| $ F\left({x, y, z} \right) = \left\{ {\begin{array}{*{20}{c}} {{c_1}{x^2} + {c_2}{y^2} \le {c_4} - {z^{c3}}, }\\ {{c_5} \le z \le {c_6}, }\\ {{c_1}{c_2} \ge 0。} \end{array}} \right. $ | (1) |
在理想的原木数学模型中,式(1)是椭圆幂函数柱体的顶点沿着z向平移,F(x, y, z)中ci可以通过实际测量获得。其中c5与c6定义了数学模型z向的定义域,c3=t,t为模型系数,当木材为理想原木模型时,t=1(任洪娥等,2008;邵忠波,2013)。
通过图 3可得到计算短径方向单板材积时x的取值范围,由此对式(1)积分,得短径方向单板的材积为:
| $ {v_x} = 2\int_{{x_1} - s}^{{x_1}} {{\rm{d}}x} \int_0^L {{\rm{d}}z} \int_0^{\sqrt {\frac{1}{{{c_2}}}\left({{c_4} - z - {c_1}{x^2}} \right)} } {{\rm{d}}y} 。 $ | (2) |

|
图 3 短径方向单板数学模型 Fig.3 The mathematical model of veneer's short trail direction |
通过式(2)可以得出精确的解析解,且远远高于传统算法的精度。为了方便计算,对该结果非线性函数进行泰勒级数展开,当展开式为3项时,误差为:
| $ {r_n} = \frac{1}{{\left({2n + 1} \right)!\left[ {2\left({n + 1} \right) + 1} \right]}} \approx 0.00119。 $ | (3) |
所以该式所得积分的结果为:
| $ \begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {{v_{1x}} = \frac{{D_{{\rm{a2}}}^2D_{{\rm{b}}1}^3L}}{{8{D_{{\rm{a1}}}}\left({D_{{\rm{b}}1}^2 - D_{{\rm{a}}1}^2} \right)}}\left\{ {\frac{{2{x_1}}}{{3{D_{{\rm{b2}}}}}}\left({5 - \frac{{8x_1^2}}{{D_{{\rm{b2}}}^2}}} \right)} \right.}\\ {\sqrt {1 - \frac{{4x_1^2}}{{D_{{\rm{b2}}}^2}}} + \frac{{2{x_1}}}{{{D_{{\rm{b2}}}}}} + \frac{{4x_1^3}}{{3D_{{\rm{b2}}}^3}} + \frac{{4x_1^5}}{{15D_{{\rm{b2}}}^5}} - } \end{array}}\\ {\frac{{2\left({{x_1} - s} \right)}}{{3{D_{{\rm{b2}}}}}}\left({5 - \frac{{8{{\left({{x_1} - s} \right)}^2}}}{{D_{{\rm{b2}}}^2}}} \right)\sqrt {1 - \frac{{4{{\left({{x_1} - s} \right)}^2}}}{{D_{{\rm{b2}}}^2}}} }\\ {\begin{array}{*{20}{c}} { - \frac{{2\left({{x_1} - s} \right)}}{{{D_{{\rm{b2}}}}}} - \frac{{4{{\left({{x_1} - s} \right)}^3}}}{{3D_{{\rm{b2}}}^3}} - \frac{{4{{\left({{x_1} - s} \right)}^5}}}{{15D_{{\rm{b2}}}^5}} - }\\ {\left[ {\frac{{2{x_1}}}{{3{D_{{\rm{b2}}}}}}\left({\frac{{5D_{{\rm{a1}}}^2}}{{D_{{\rm{a2}}}^2}} - \frac{{8x_1^2}}{{D_{{\rm{b2}}}^2}}} \right) + \frac{{2D_{{\rm{a1}}}^3{x_1}}}{{D_{{\rm{a2}}}^3{D_{{\rm{b}}2}}}} + \frac{{4{D_{{\rm{a1}}}}x_1^3}}{{3{D_{{\rm{a}}2}}D_{{\rm{b}}2}^3}}} \right.}\\ { + \frac{{4{D_{{\rm{a2}}}}x_1^5}}{{15{D_{{\rm{a1}}}}D_{{\rm{b}}2}^5}} - \frac{{2\left({{x_1} - s} \right)}}{{3{D_{{\rm{b2}}}}}}\left({\frac{{5D_{{\rm{a1}}}^2}}{{D_{{\rm{a2}}}^2}} - \frac{{8{{\left({{x_1} - s} \right)}^2}}}{{D_{{\rm{b2}}}^2}}} \right)}\\ {\sqrt {\frac{{D_{{\rm{a1}}}^2}}{{D_{{\rm{a2}}}^2}} + \frac{{4{{\left({{x_1} - s} \right)}^2}}}{{D_{{\rm{b2}}}^2}}} - \frac{{2D_{{\rm{a1}}}^3\left({{x_1} - s} \right)}}{{D_{{\rm{a2}}}^3{D_{{\rm{b2}}}}}} - } \end{array}}\\ {\left. {\left. {\frac{{4{D_{{\rm{a1}}}}{{\left({{x_1} - s} \right)}^3}}}{{3{D_{{\rm{a2}}}}D_{{\rm{b}}2}^3}} - \frac{{4{D_{{\rm{a2}}}}{{\left({{x_1} - s} \right)}^5}}}{{15{D_{{\rm{a1}}}}D_{{\rm{b}}2}^5}}} \right]} \right\}。} \end{array} $ | (4) |
可以看出式(4)的结果非常复杂,事实上,其结果与近似积分结果相差非常小,而且可以认为模型系数在任意数值下。在式(4)中,对y向积分后再积分z向时,将其根号进行线性化,只取其牛顿二项式的线性项,则式(4)的积分结果(马岩等,1994)为:
| $ \begin{array}{*{20}{c}} {{v_x} = \frac{1}{4}{D_{{\rm{a1}}}}{D_{{\rm{b1}}}}L\left({\frac{{D_{{\rm{a1}}}^2 + tD_{{\rm{a2}}}^2}}{{D_{{\rm{a1}}}^2\left({1 + t} \right)}}} \right)\left[ {\frac{{2{x_1}}}{{{D_{{\rm{b2}}}}}} + \frac{{4x_1^3}}{{3D_{{\rm{b}}2}^3}}} \right. + }\\ {\frac{{4x_1^5}}{{15D_{{\rm{b}}2}^5}} - \frac{{2\left({{x_1} - s} \right)}}{{{D_{{\rm{b2}}}}}} - \frac{{4{{\left({{x_1} - s} \right)}^3}}}{{3D_{{\rm{b}}2}^3}} - }\\ {\frac{{4{{\left({{x_1} - s} \right)}^5}}}{{15D_{{\rm{b}}2}^5}} + \frac{{D_{{\rm{a2}}}^2\left({1 + t} \right)}}{{tD_{{\rm{a2}}}^2 + D_{{\rm{a1}}}^2}}\left({\frac{{2{x_1}}}{{{D_{{\rm{b2}}}}}}\sqrt {1 - \frac{{4x_1^2}}{{D_{{\rm{b}}2}^2}}} } \right.}\\ {\left. {\left. { - \frac{{2\left({{x_1} - s} \right)}}{{{D_{{\rm{b2}}}}}} \times \sqrt {1 - \frac{{4{{\left({{x_1} - s} \right)}^2}}}{{D_{{\rm{b}}2}^2}}} } \right)} \right]。} \end{array} $ | (5) |
同理,可以求出长径方向单板的材积为:
| $ \begin{array}{*{20}{c}} {{v_y} = \frac{1}{4}{D_{{\rm{a1}}}}{D_{{\rm{b1}}}}L\left({\frac{{D_{{\rm{a1}}}^2 + tD_{{\rm{a2}}}^2}}{{D_{{\rm{a1}}}^2\left({1 + t} \right)}}} \right)\left[ {\frac{{2{y_1}}}{{{D_{{\rm{a2}}}}}} + \frac{{4y_1^3}}{{3D_{{\rm{a}}2}^3}}} \right. + }\\ {\frac{{4y_1^5}}{{15D_{{\rm{a}}2}^5}} - \frac{{2\left({{y_1} - s} \right)}}{{{D_{{\rm{a2}}}}}} - \frac{{4{{\left({{y_1} - s} \right)}^3}}}{{3D_{{\rm{a}}2}^3}} - }\\ {\frac{{4{{\left({{y_1} - s} \right)}^5}}}{{15D_{{\rm{a}}2}^5}} + \frac{{D_{{\rm{a2}}}^2\left({1 + t} \right)}}{{tD_{{\rm{a2}}}^2 + D_{{\rm{a1}}}^2}}\left({\frac{{2{y_1}}}{{{D_{{\rm{a2}}}}}}\sqrt {1 - \frac{{4y_1^2}}{{D_{{\rm{a}}2}^2}}} } \right.}\\ {\left. {\left. { - \frac{{2\left({{y_1} - s} \right)}}{{{D_{{\rm{a2}}}}}} \times \sqrt {1 - \frac{{4{{\left({{y_1} - s} \right)}^2}}}{{D_{{\rm{a}}2}^2}}} } \right)} \right]。} \end{array} $ | (6) |
双面刨切单板出材率是衡量木材加工效益的主要标准,出材率越高,效益也越高。双面刨切单板出材率是指经双面刨切后,小径木加工所得合格单板所占小径木整体材积的比例,即:
| $ 双面刨切出材率 = \frac{合格单板材积}{小径木整体材积}。 $ | (7) |
式(7)中,双面刨切所得合格单板体积计算公式已经在上一节计算得到,本节不再赘述。小径木整体体积VT计算如下:
| $ {v_{\rm{T}}} = 4\int_0^{{D_{{\rm{b1}}}}} {{\rm{d}}x} \int_0^L {{\rm{d}}z} \int_0^{\sqrt {\frac{1}{{{c_2}}}\left({{c_4} - z - {c_1}{x^2}} \right)} } {{\rm{d}}y} 。 $ | (8) |
由此计算可以得到出材率结果,但是计算过程复杂,且计算难度较大。在式(8)中,合格单板面积与小径木整体面积都涉及相同的小径木高度,其高度可以约分,因此出材率计算可直接计算合格单板与小径木底面积之比,即:
| $ 双面刨切单板出材率 = \frac{合格单板底面积}{小径木底面积}。 $ | (9) |
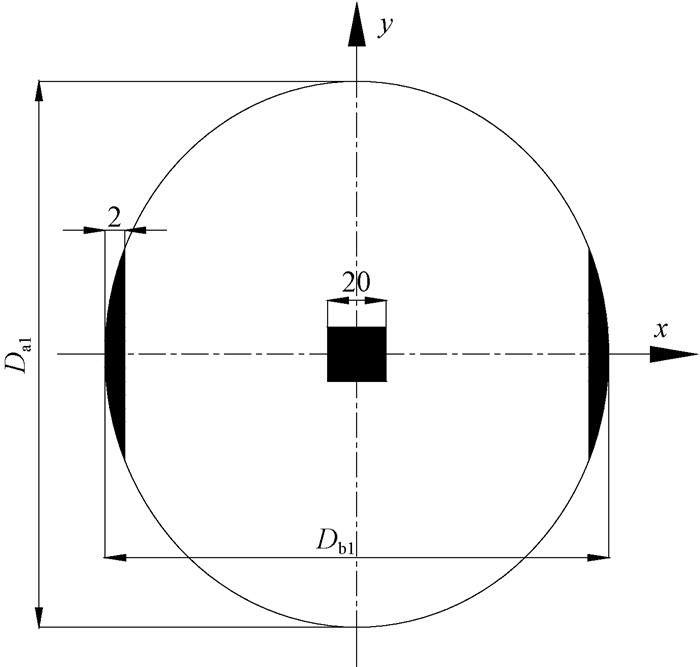
由中间固定板处理工艺可知,中间固定芯板叠加起来重新刨切后,每块固定芯板仅剩余20 mm×20 mm的芯材需要丢弃,即每棵加工小径木废弃料只有两侧板皮及中间剩余芯材。如图 4所示,小径木截面为一椭圆,其中中间20 mm×20 mm的阴影部分为需要丢弃的芯材,两侧阴影部分为需要丢弃的板皮,截面空白部分为合格单板的截面。因为直接计算空白面积难度较大,所以通过计算阴影部分即废弃料面积,然后总截面与废弃料相减即可得到结果,而废弃材料截面积可以通过芯材与板皮截面积相加得到,计算如下:
|
图 4 小径木横截面 Fig.4 The cross section of small-diameter wood |
图 4中,Da1为小径木小头横截面椭圆短径,Db1为其长径,S为小径木截面面积,S1为单侧板皮截面积,S2为中间芯材面积,S3为合格单板截面面积。所以建立椭圆方程:
| $ \;\frac{{{y^2}}}{{{{\left({{D_{{\rm{a1}}}}/2} \right)}^2}}} + \frac{{{x^2}}}{{{{\left({{D_{{\rm{b1}}}}/2} \right)}^2}}}1。 $ | (10) |
因为x取值范围已知,取值区间即为板皮厚度,所以对椭圆方程进行因变量y的积分可得单侧板皮截面积S1:
| $ {S_1} = 2\int_{\frac{{{D_{{\rm{b1}}}}}}{2} - 2}^{\frac{{{D_{{\rm{b1}}}}}}{2}} {} \sqrt {\frac{{D_{{\rm{a1}}}^2}}{4}\left({1 - \frac{{4{x^2}}}{{D_{{\rm{b1}}}^2}}} \right)} {\rm{d}}x。 $ | (11) |
对式(11)进行求解得到结果:
| $ \begin{array}{*{20}{c}} {{S_1} = \frac{{{D_{{\rm{a1}}}}{D_{{\rm{b1}}}}}}{2}\left({\frac{1}{2}{\theta _x}\left| {\begin{array}{*{20}{c}} {\frac{{\rm{\pi }}}{2}}\\ {\arcsin \left({1 - \frac{4}{{{D_{{\rm{b1}}}}}}} \right)} \end{array} + } \right.} \right.}\\ {\left. {\left. {\left({\frac{1}{4}\sin 2{\theta _x} + {c_0}} \right)} \right|\begin{array}{*{20}{c}} {\frac{{\rm{\pi }}}{2}}\\ {\arcsin \left({1 - \frac{4}{{{D_{{\rm{b1}}}}}}} \right)} \end{array}} \right)。} \end{array} $ | (12) |
式(12)中θx与椭圆方程关系为:
| $ \sin {\theta _x} = \frac{{2x}}{{{D_{{\rm{b1}}}}}}。 $ | (13) |
由图 4很容易得到中间芯材截面积S2:
| $ {S_2} = 20 \times 20 = 400\left({{\rm{m}}{{\rm{m}}^2}} \right)。 $ | (14) |
小径木椭圆截面面积S:
| $ S = {\rm{\pi }}{D_{{\rm{a1}}}}{D_{{\rm{b1}}}}/4。 $ | (15) |
同时也很容易得到合格单板面积S3:
| $ {S_3} = S - 2{S_1} - {S_2}。 $ | (16) |
所以将式(11),(14),(15),(16)带入式(17)中可得小径木出材率η:
| $ \begin{array}{*{20}{c}} {\eta = \frac{{S - 2{S_1} - {S_2}}}{S} \times 100\% = }\\ \begin{array}{l} \frac{{{\rm{\pi }}{D_{{\rm{a1}}}}{D_{{\rm{b1}}}}/4 - 400 - {D_{{\rm{a1}}}}{D_{{\rm{b1}}}}\left[ {\left({\frac{1}{2}{\theta _x} + \frac{1}{4}\sin 2{\theta _x} + {c_0}} \right)\left| {\begin{array}{*{20}{c}} {\frac{{\rm{\pi }}}{2}}\\ {\arcsin \left({1 - \frac{4}{{{D_{{\rm{b1}}}}}}} \right)} \end{array}} \right.} \right]}}{{{\rm{\pi }}{D_{{\rm{a1}}}}{D_{{\rm{b1}}}}/4}}\\ \times 100\% 。 \end{array} \end{array} $ | (17) |
利用式(17)可对小径木双面刨切单板进行出材率的近似计算。
为了得到实际小径木双面刨切单板的出材率,对将要进行刨切的小径木进行实际参数的测量,将得到实际参数带入式(17)中即可对出材进行估算。一般情况下,小径木短径区间是50~200 mm,最大的不会多于300 mm。通过实际测量得到4组典型小径木参数,计算后得到出材率如表 1。
|
|
在本试验中,所讨论对象是无节子、径向无弯曲度的理想小径木,为了简化其计算过程,取小径木截底面椭圆度保持不变,一直为10/11(汤晓华,2002)。但在实际情况中,如果小径木弯曲度每增加1%,出材率将降低8%~10%,且其椭圆度也是不断发生变化的,也将影响小径木的出材率。本计算数据主要提供不同小径木双面刨切单板出材率比较,从而合理选择小径木进行双面刨切,在实际计算中需根据特殊情况进行重新处理。
4 结论本文分别从短径方向和长径方向对刨切单板精确地进行了材积计算,而精确的材积计算不是为了计算其材积,而是为刨切时提供精确下刀的基础;双面刨切单板工艺不仅节省了时间,而且减少了人力,大大提高了加工效率;并且在双面刨切中加入了中间固定芯板的处理工艺,很大程度上提高了小径木双面刨切的出材率,对于实际加工来说有很大的经济效益。通过出材率实际分析计算得出,当小径木直径较大时,出材率相应较高,反之则较低。所以在实际小径木刨切时,应尽量选用尺寸较大的小径木,从而提高小径木的出材率,避免木材资源的浪费,提高经济效益。
| [] |
李伟光. 2008. 单板刨切技术的现状与发展. 木材加工机械 (12) : 37–39.
( Li W G.2008. The discussion on the technology of veneer slicing. Wood Processing Machinery (12) : 37–39. [in Chinese] ) |
| [] |
刘孝岷. 2008. 影响单板出板率的因素及优化措施. 科技信息(科学教研) (24) : 21.
( Liu X M.2008. The factors affecting the rate of veneer and optimization measures. Science & Technology Information (24) : 21. [in Chinese] ) |
| [] |
刘玉娟, 徐凯宏, 马岩, 等. 2011. 数控裁板锯的下锯优化研究. 制造业自动化 , 33 (10) : 10–13.
( Liu Y J, Xu K H, Ma Y, et al.2011. The study of cutting optimization of CNC panel saw. Manufacturing Automation , 33 (10) : 10–13. [in Chinese] ) |
| [] |
刘玉善. 2012. 人工速生材和小径木加工利用的途径与方法. 林业科技 , 37 (3) : 62.
( Liu Y S.2012. The ways and methods of processing and utilizing the fast-growing wood and small-diameter wood. Forestry Science , 37 (3) : 62. [in Chinese] ) |
| [] |
陆贵添. 2012. 材积的计算分类与整合计算. 吉林农业 , 263 (1) : 139–140.
( Lu G T.2012. The calculation of classification and integration of volume. Jilin Agriculture , 263 (1) : 139–140. [in Chinese] ) |
| [] |
马岩. 1990. 理想原木材积通式和缺陷原木模型和材积推导. 东北林业大学学报 , 18 (19) : 81–94.
( Ma Y.1990. Common scale formulation of ideal log and model and scale detecting fault log research. Journal of Northeast Forestry University , 18 (19) : 81–94. [in Chinese] ) |
| [] |
马岩, 白雪晶, 孟庆波, 等. 1994. 理想原木钝棱扁方材BOF的实用精确解析解推导. 东北林业大学学报 , 22 (1) : 81–85.
( Ma Y, Bai X J, Meng Q B, et al.1994. The practical exact analytic results of BOF on the flat square-edge of ideal log. Journal of Northeast Forestry University , 22 (1) : 81–85. [in Chinese] ) |
| [] |
马岩. 2006. 国际木工刨床设计新技术综述. 木工机床 (4) : 5–8.
( Ma Y.2006. The overview of international new technology to design wood planer. Woodworking Machinery (4) : 5–8. [in Chinese] ) |
| [] |
马岩. 2011. 重组木技术发展过程中存在的问题分析. 中国人造板 (2) : 1–5.
( Ma Y.2011. Hurdles in industrialization process of the scrimber technology. China Wood-Based Panels (2) : 1–5. [in Chinese] ) |
| [] |
任洪娥, 袁旭, 马岩. 2008. 弓形弯曲原木优化下锯建模与仿真. 林业机械与木工设备 , 36 (2) : 35–38.
( Ren H E, Yuan H, Ma Y.2008. BOF modeling and simulation of bow-bending log. Forestry Machinery & Woodworking Equipment , 36 (2) : 35–38. [in Chinese] ) |
| [] |
邵忠波. 2013. 木材材积计算方法的探讨. 科技创新与应用 (23) : 293–294.
( Shao Z B.2013. The discussion on the calculation method of wood volume. Technology Innovation and Application (23) : 293–294. [in Chinese] ) |
| [] |
孙义刚, 车仁君, 宋俊杰. 2010. 刨切机与旋切机、刨切单板与旋切单板的比较. 林业机械与木工设备 , 38 (5) : 4–5, 15.
( Sun Y G, Che R J, Song J J.2010. Comparisons between slicers and rotary lathes sliced veneer and rotary cut veneer. Forestry Machinery & Woodworking Equipment , 38 (5) : 4–5, 15. [in Chinese] ) |
| [] |
汤晓华. 2002.旋切六点定心理论及数学模拟研究.哈尔滨:东北林业大学硕士学位论文. ( Tang X H. 2002. Research on the peeling six points centering theory and mathematics simulation. Harbin:MS thesis of Northeast Forestry University. [in Chinese][in Chinese]) http://cdmd.cnki.com.cn/Article/CDMD-10225-2002121816.htm |
| [] |
王宏棣. 2007. 人工林小径结构用材的现状与发展趋势. 林业机械与木工设备 , 35 (3) : 13–14.
( Wang H D.2007. Current situation and development trend of small diameter lumber from plantation forests in application as structural lumber. Forestry Machinery & Woodworking Equipment , 35 (3) : 13–14. [in Chinese] ) |
| [] |
王晓欢, 费本华, 赵荣军, 等. 2009. 木质重组材料研究现状与发展. 世界林业研究 , 22 (3) : 58–63.
( Wang X H, Fei B H, Zhao R J, et al.2009. Status and progress of wood recom-binant materials. World Forestry Research , 22 (3) : 58–63. [in Chinese] ) |
| [] |
于文吉. 2013. 我国木、竹重组材产业发展的现状与前景. 木材工业 , 27 (1) : 5–8.
( Yu W J.2013. Development and prospect of wood and bamboo scrimber industry in China. China Wood Industry , 27 (1) : 5–8. [in Chinese] ) |
| [] |
余养伦, 于文吉. 2013. 新型纤维化单板重组木的主要制备工艺与关键设备. 木材工业 , 27 (5) : 5–8.
( Yu Y L, Yu W J.2013. Manufacturing technology of novel scrimber made of fibrosis of veneer. China Wood Industry , 27 (5) : 5–8. [in Chinese] ) |
| [] |
周兰美, 马大国, 贾娜, 等. 2004. 单板刨切与旋切的比较. 林业机械与木工设备 , 32 (3) : 45–46.
( Zhou L M, Ma D G, Jia N, et al.2004. Comparison between veneer slicing and peeling. Forestry Machinery & Woodworking Equipment , 32 (3) : 45–46. [in Chinese] ) |
| [] | Aguilera A, Vega M, Méausoone P J.2007. Effects of grain angle on the amplitudes of acoustic emission and surface roughness in wood machining. Wood Science and Technology , 41 (4) : 373–381. DOI:10.1007/s00226-006-0117-2 |
| [] | Olufemi B.2012. Yield and mechanical properties of veneer from Brachystegia nigerica. Journal of Forestry Research , 23 (2) : 295–298. DOI:10.1007/s11676-012-0255-3 |
| [] | Jin W Z.2001. Comparison and analysis of the main technological factors of influencing mechanical properties of scrimber and PSL. Journal of Forestry Research , 12 (4) : 266–268. DOI:10.1007/BF02856721 |
| [] | Sheikh-Ahmad J Y, Bailey J A.1999. High-temperature wear of cemented tungsten carbide tools while machining particleboard and fiberboard. Journal of Wood Science , 45 (6) : 445–455. DOI:10.1007/BF00538952 |
 2016, Vol. 52
2016, Vol. 52

