文章信息
- 尤磊, 唐守正, 宋新宇
- You Lei, Tang Shouzheng, Song Xinyu
- 基于切平面投影的树干三维表面重建算法
- An Algorithm of Stem Surface Reconstruction Based on Tangent Plane Projection
- 林业科学, 2016, 52(11): 115-123
- Scientia Silvae Sinicae, 2016, 52(11): 115-123.
- DOI: 10.11707/j.1001-7488.20161114
-
文章历史
- 收稿日期:2016-02-02
- 修回日期:2016-07-06
-
作者相关文章
2. 中国林业科学研究院资源信息研究所 北京 100091;
3. 信阳师范学院数学与信息科学学院 信阳 464000
2. Research Institute of Forest Resource and Information Techniques, CAF Beijing 100091 ;
3. College of Mathematics and Information Science, Xinyang Normal University Xinyang 464000
随着计算机图形学、虚拟现实以及三维激光扫描技术的发展,将三维激光扫描仪应用于林业相关领域是当前的研究热点。其研究内容大致分为2类:1)树木的形态模拟与重建;2)树木的参数提取。
Pfeifer等(2004a)使用分段拟合圆柱体的方式构建了树干模型;Pfeifer等(2004b)使用B-样条曲线拟合了树干横断面;Gorte等(2004a;2004b)使用树木形态学方法填充树干,再分段拟合圆柱体构建了树木的三维圆柱体表面;Xu等(2007)在有向加权图中使用最短路径合成树干与树枝的骨架,基于树木的结构化特征使用异速生长律构建了树木的多边形模型;高士增等(2013)提取树木不同高度处的凸包构建了等值线,在等值线间构建不规则三角网以重建树木的表面模型;黄洪宇等(2013)概述了树木三维建模方法与使用激光点云对单木建模的基本原理与基本过程;王晓辉等(2014)根据树木的几何拓扑原理设计开发了一套交互式的基于点云的树木三维建模系统;Hackenberg等(2015)设计开发了一套名为SimpleTree的开源单木模拟系统,使用圆柱体拟合树木点云构建了单木模型。
上述研究尽管取得了较好的视觉效果,但都是对树木或树干的模拟重建,特别是对树干的模拟重建。这些研究多关注树干的整体形态结构,并没有关注树干局部表面的特征;然而树干直径、断面积、材积等参数与树干表面局部特征关系密切,因此此类模拟重建方法难以用于树干参数的精确提取。树干作为树木的一个重要组成部分,在林业生产与研究中具有极其重要的地位。考虑到构建树干模型是森林景观与树木可视化的基础环节,树干参数是林业相关研究的基础数据,故本文仅以树干的表面重建为研究内容,暂不考虑树木其他部位的表面重建。
树干具有如下特征:形状复杂,不同位置有不同程度的弯曲与扭曲,树干表面粗糙、凸凹不平;在外业扫描时,因地面三维激光扫描仪与树干不同高度处的距离不同,且受风扰、遮挡等因素的影响,导致树干点云密度差异较大、树干点云中存在着离散噪声点。这些都为构建树干的精确表面模型带来了不少困难。
二维平面点集上的Delaunay不规则三角网具有最小角最大化与空外接圆特性,这保证了平面点集三角剖分的唯一性与合理性(De Berg et al., 2009)。然而二维平面点集上的Delaunay三角剖分无法直接扩展到三维空间点集的Delaunay表面重建上(袁方等,2011)。Gopi等(2000)提出基于切平面投影将点集投影至二维平面上,将构建的二维Delaunay三角网的连接关系映射到三维空间中以实现表面重建。张剑清等(2011)在Gopi等(2000)的基础上优化了法向量的计算方法。
本研究在Gopi等(2000)与张剑清等(2011)的基础上,根据树干点云特征对基于切平面投影的表面重建算法进行改进,并将其应用于树干点云的表面重建。本文中,如果不做特别说明,重建的表面模型是指不规则三角网表面模型。
1 材料与方法 1.1 试验数据获取以2次外业扫描的树干点云作为试验数据。第1次扫描的是杨树(Populussp.),先使用绿色油漆标注树号再扫描。第2次扫描洋白蜡(Fraxinus pennsylvanica)2株、大叶白蜡(Fraxinus chinensisvar.rhynchophylla)1株(树高80 cm处有明显的凹陷)、一球悬铃木(Platanus occidentalis)1株、臭椿(Ailanthus altissima)1株及一端去皮后的一段落叶松(Larix gmelinii)原木(室内扫描)。先使用围尺在树干不同高度测量直径,共获取直径数据31条,再使用彩色粉笔沿着围尺轨迹标注测径轨迹,并使用颜色各异、大小不同的彩色纸条标注树干方位,最后使用地面三维激光扫描仪扫描。2次外业均使用FARO X330地面三维激光扫描仪,扫描精度为1/4,扫描速度为122 kpts ·s-1。使用FARO Scene 5.0软件对扫描点云进行配准,然后移除地表及枝桠点云后得到树干点云。
1.2 树干点云表面重建算法 1.2.1 相关定义为了便于描述,先介绍解析几何中切平面、法向量(尤承业,2004)与点云集中切平面的相关定义。
平面的法向量:设平面τ的方程为Ax+By+Cz+D=0,向量
切平面:曲面上过点Pi的曲线在点Pi处的切线都与向量
| $ \left({q - {P_i}} \right){{\hat n}_i}=0. $ | (1) |
式中:q是切平面Ti上任意一点。
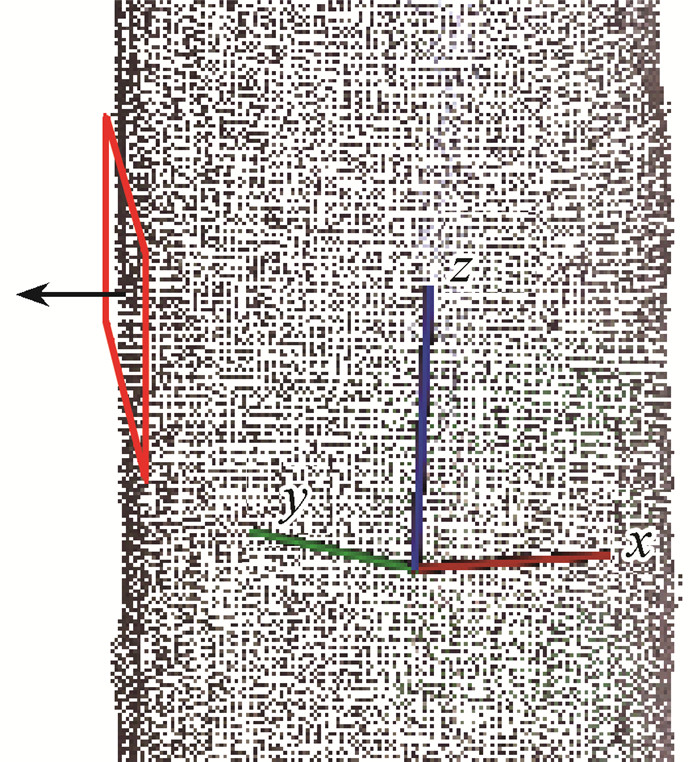
点集P在点Pi处的切平面:对于树干点云集P中的一点Pi,树干在点Pi处的表面在点Pi处的切平面Ti称为点集P在点Pi处的切平面,切平面Ti的法向量称为点集P在点Pi处切平面的法向量。因树干表面的粗糙性,很难用一个具体、精确的曲面方程来描述树干在点Pi处的表面,因此,本研究采用点Pi与其附近的邻域点计算点集P在点Pi处切平面的参数,如图 1所示。
|
图 1 树干点云的切平面 Fig.1 Tangent plane of stem point cloud 图中矩形代表切平面,箭头所示方向为切平面法向量的方向。 The rectangle represents the tangent plane of a point. The arrow direction is the normal vector direction of the tangent plane. |
Delaunay近邻点:平面点集上,与点Pi构成一个Delaunay三角形的另外2个顶点称为Pi的Delaunay近邻点。
1.2.2 算法概述图 2是基于切平面投影的表面重建算法流程,其中N为树干点云的点云总个数。受设备扫描时风扰产生噪声及点云配准等因素影响,树干点云可能会在一些区域相互重叠,会导致此区域出现重影而无法准确定义表面的位置。为此,首先对树干点云进行下采样与删除离散噪声点预处理,这也是点云表面重建的基本步骤之一(朱德海,2012)。

|
图 2 算法流程 Fig.2 The flowchart of the algorithm |
下面分步介绍算法的实现过程。
1)数据预处理离散噪声点通过给定半径范围内邻域点的数量来判定。当点Pi在邻域半径Rn范围内邻域个数小于Nn时,点Pi就是离散噪声点。
根据树干点云构建三维体素栅格,其中每个三维体素栅格规格为lxcm×lycm×lzcm。下采样时,每个体素由该体素内所有点的重心点表示。
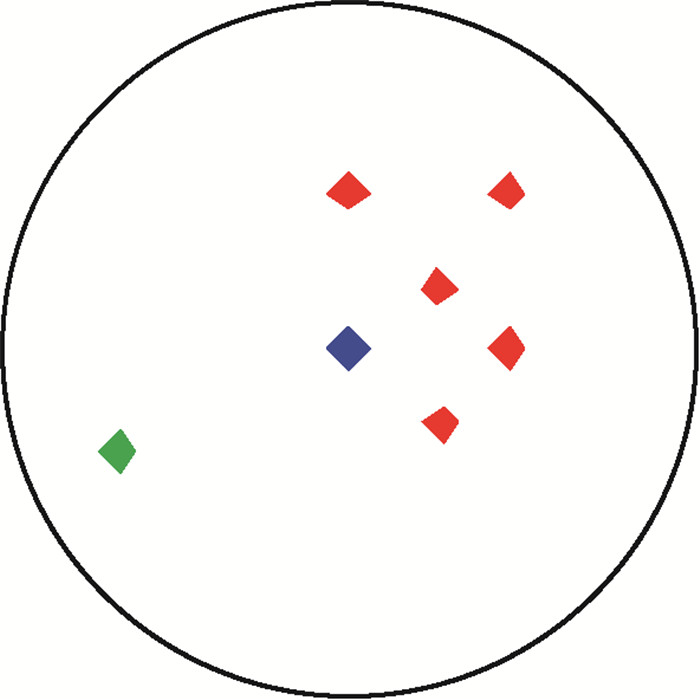
2)邻域集的选择准则对于树干点云集P中的1个点Pi,其邻域点集Ωi决定了与点Pi构成三角形面片的其他顶点。Gopi等(2000)与张剑清等(2011)均使用k个近邻点(k-nearest)获取邻域点。受树干表面粗糙性及扫描时受遮挡的影响,点Pi的邻域点分布可能不均匀,有可能出现一侧邻域点密集而另一侧邻域点稀少的情况。在重建表面时,点Pi与其四周的邻域点构成三角形,考虑到与点Pi构成三角形的邻域点的不确定性,很难选定一个合适的k值以适合所有点的表面重建。如图 3所示,当k=5时,蓝色点的邻域点不包括绿色点。
|
图 3 点云密度分布不均匀 Fig.3 The density of point cloud is uneven |
邻域点集的选择不仅关系到切平面的构建,也关系到邻域点集在切平面投影的拓扑结构。图 3中, 绿色点的加入会改变切平面的法向量,导致点集在切平面的投影位置发生变化,从而影响点之间的构网关系。因此,邻域点集的选择对重建表面的影响较大。
在三维空间中,点Pi的邻域半径Rs形成一个以点Pi为圆心、以半径为Rs的球体。相对于邻域个数而言,采用邻域半径则更容易获取点四周的邻域点,因此,本研究采用邻域半径值Rs选择邻域点,Pi的邻域点集Ωi表示为:
| $ {\mathit{\Omega }_\mathit{i}}=\left\{ {{P_j}\left| {\left\| {{P_i} - {P_j}} \right\| <{R_s}, {P_i}, {P_j} \in P} \right.} \right\}. $ | (2) |
3)切平面的简化构建及投影计算切平面法向量的计算以邻域点集Ωi为数据基础。显然,到点Pi距离越近的点,其对树干在点Pi处的切平面的影响越大。张剑清等(2011)以点Pi为中心点构建协方差矩阵计算切平面法向量,并未考虑距离对切平面的影响。本研究采用Cheng等(2006)使用的加权协方差矩阵计算切平面的法向量。定义加权系数为:
| $ {w_j}=w\left({\left\| {{P_j} - {P_i}} \right\|/n} \right). $ | (3) |
式中,n为Pi邻域点的个数,加权函数使用wendland径向基函数:
| $ w\left(x \right)={\left({1 - x} \right)^4}\left({1+4x} \right). $ | (4) |
则加权协方差矩阵可表示为:
| $ M=\sum\limits_{{P_i}, {P_j} \in \mathit{\Omega }, j \ne i} {{{\left[ {{w_j}\left({{P_j} - {P_i}} \right)} \right]}^{\rm{T}}}} \left[ {{w_j}\left({{P_j} - {P_i}} \right)} \right]. $ | (5) |
矩阵M的最小特征值对应的特征向量即为切平面的法向量
Gopi等(2000)与张剑清等(2011)均对法向量的方向进行了归一化处理。对于基于切平面的重建算法,此过程可以省略。
切平面的作用是获取点Pi与其邻域点在切平面上投影的几何拓扑关系。一旦确定切平面的法向量,即可构建无数个与切平面Ti相平行的平面。根据点到平面投影的定义可知,点集Ωi投影到与切平面平行的任何一个平面,其投影点集Ωi′中点之间的几何拓扑关系是不变的,在一个平面上的投影等价于另一个平行平面投影的平移,因此,确定了切平面的法向量即确定了投影集中点之间的拓扑关系,也就确定了二维Delaunay三角网的网络结构,从而无须对切平面法向量进行归一化处理,也无须计算过点Pi的切平面Ti的方程,只需使用过坐标原点o且法向量为
| $ \left({q - o} \right){{\hat n}_i}=0. $ | (6) |
值得注意的是,树干表面的粗糙性可能会使Ωi中不同的点在切平面Ti上的投影点重合,这会导致此投影点集下无法构建正确的Delaunay三角网。根据点距离越远、点之间相互影响越小的思想,若出现重合的投影点,则在投影点集中删除距离点Pi较远的邻域点的投影点。
4)投影点集的旋转因投影平面是一个三维空间上的平面,故投影点集Ωi′是一个三维空间中的平面点集。因平面Delaunay三角网的构建算法一般都是在二维XY平面上实现的,因此构建三维平面的Delaunay三角网可以有2种方案:(1)实现三维平面上的Delaunay三角网构网算法;(2)将三维平面点集转换到二维XY平面上,在二维XY平面上构建Delaunay三角网。张剑清等(2011)采用第2种方案,通过构建三维平面上的一组正交单位向量将点逐一分解以转换到二维XY平面上,这种方法依赖于正交单位向量的选择且计算较为复杂。
本研究使用一种简单有效的方法:将三维平面点集旋转至与XY平面平行,这等价于将三维平面点集的法向量
| $ R\left(\beta \right){R_x}\left(\alpha \right)=\left[ {\begin{array}{*{20}{c}} {\cos \beta }&{ - \sin \alpha \sin \beta }&{\cos \alpha \sin \beta }\\ 0&{\cos \alpha }&{ - \sin \alpha }\\ {\sin \beta }&{in\alpha \cos \beta }&{\cos \alpha \cos \beta } \end{array}} \right]; $ | (7) |
| $ \alpha=\left\{ \begin{array}{l} \arcsin \left[ {{y_i}/{\rm{sqrt}}\left({y_i^2+z_i^2} \right)} \right], y_i^2+z_i^2 \ne 0, \\ 0, y_i^2+z_i^2=0; \end{array} \right. $ | (8) |
| $ \beta=\arcsin \left[ {{x_i}/{\rm{sqrt}}\left({x_i^2+y_i^2+z_i^2} \right)} \right]. $ | (9) |
5)二维Delaunay三角网的构建 Gopi等(2000)与张剑清等(2011)均根据Delaunay三角网与Voronoi图的等价性,通过搜索点Pi′(点Pi在二维平面上的投影点)的邻近区域的边界来确定Pi′的Delaunay近邻点,这种方法计算复杂。本研究使用尤磊等(2016)提出的以优先点为中心的Delaunay构网算法在XY平面上构建点集Ωxy, i′的Delaunay三角网。根据Delaunay三角网中点Pi′与其他点的连接关系得到Delaunay近邻点。
6)三维Delaunay三角网的构建 将点Pi′与其Delaunay近邻点的连接关系映射到树干点云上,构成以Pi为顶点的多个三角形面片,完成点Pi的表面重建。
对树干点云中的每个点逐一执行上述重建过程,即可完成每个点的表面重建。若3个点Pi-1、Pi与Pi+1互为近邻点,则这3个点重建的表面中都包括ΔPi-1PiPi+1。因此,在完成所有点的表面重建后删除重建表面上重复的三角形即得到树干三维不规则三角网的重建表面。
7)算法参数列表 算法需要使用的参数如表 1所示。
|
|
点云下采样后,1个体素栅格中只有1个点,当下采样规格在3个维度上的值都相等,即满足lx=ly=lz时,相邻体素中点间距离的最小值为0,最大值为2lx。因此,在对下采样后的树干点云进行表面重建时,应使用2lx作为重建的邻域半径值,这样可以尽可能少地漏掉邻域点。
8)表面模型的定量评价 树皮的粗糙性会通过树干点云间接反映在重建的树干表面上。在相同位置,从重建的树干表面上提取的直径与使用围尺测量的直径越接近,重建表面的效果越好。由此,本研究提出一种定量化评价树干重建表面模型的方法:根据围尺测量的直径与从重建树干表面上对应位置处提取直径的差异来评价树干的重建表面模型。对应的评价指标如下:
| $ MAPE=100{\rm{ \times }}\frac{1}{n}\sum\limits_{i=1}^n {\left| {{D_i} - {{\hat D}_i}} \right|/{D_i};} $ | (10) |
| $ {\rm{RMSE=}}\sqrt {\frac{1}{n}\sum\limits_{i=1}^n {{{\left({{D_i} - {{\hat D}_i}} \right)}^2}} }. $ | (11) |
式中:Di为围尺实测直径;
从树干重建表面上提取直径的过程如下:根据外业时使用彩色粉笔标注的围尺轨迹提取树干点云,由此构建2个相互平行的横切面,使得围尺轨迹刚好位于2个横切面之间,这2个横切面称为上下限平面;然后再构建多个平行的平面且位于上下限平面之间,根据这些平面与重建的树干三维表面上多边形的相交关系得到重建表面上的横断面点云;将横断面点云投影至上限平面上得到平面投影点云,再通过模拟围尺测径的方式提取树干直径。
2 结果与分析本研究在型号ThinkCenterM8500t、内存8GB、处理器I7-4770的台式机上,采用VC++2010开发环境,使用PCL点云库(Rusu et al., 2011)中点云操作相关的类开发试验程序,从外业扫描的树木点云中提取树干点云作为试验数据集。
2.1 与经典算法对比试验Gopi等(2000)与张剑清等(2011)描述的切平面重建算法为经典算法,本文的算法为改进算法。因切平面邻域点集的选择对重建表面的效果影响较大,因此本文仅以邻域点集的不同来体现经典算法与改进算法的差异。经典算法以邻域点个数k选择邻域点集,改进算法以邻域半径Rs选择邻域点集。对于采用默认规格下采样后的树干点云,因下采样后1个栅格中只有1个点,且因1个三维栅格最多与8个三维栅格相邻,因此经典算法以k=8选择邻域点集;根据上述,改进算法以Rs=1 cm选择邻域点集。
以树号标识清晰的一段杨树的树干点云为例展示2种算法重建树干表面的可视化效果,如图 4所示。

|
图 4 不同算法重建的表面 Fig.4 Surface reconstructed by different algorithms a.经典算法Classic; b.改进算法Improved. |
经典算法重建的树干表面上有很多空洞,如图 4a中红色方框所示(此处标注了几个代表性的空洞),出现空洞的主要原因是未能准确获取点的邻域点集。
2.2 改进算法的表面重建试验结果使用改进算法对外业扫描获取的树干点云进行表面重建均取得了较好的视觉效果,本文展示3个有代表意义的树干重建表面模型。
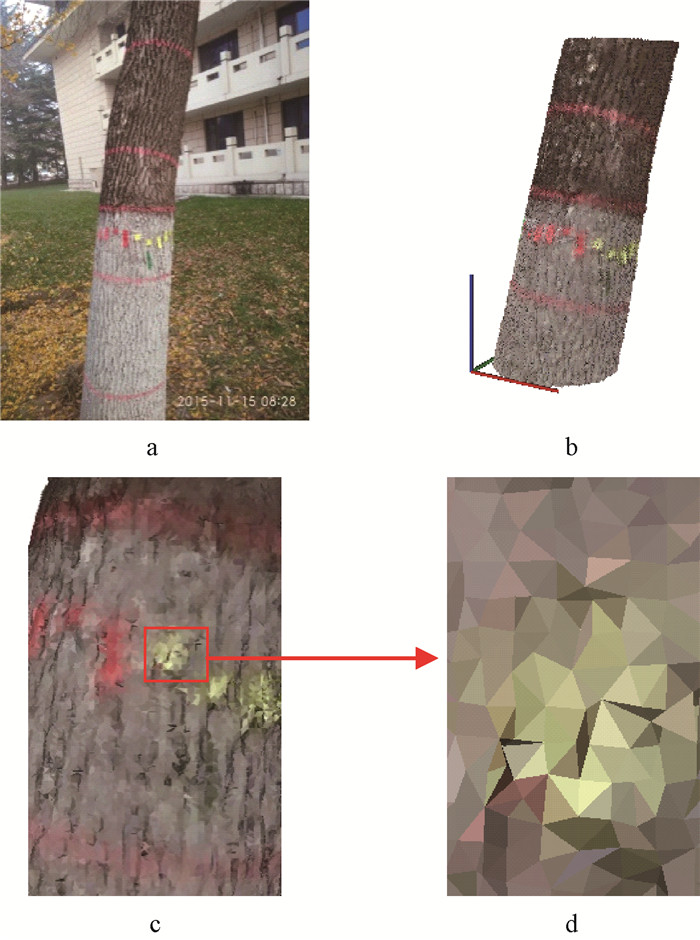
图 5是一段长度为100 cm的杨树树干表面重建的效果,图 6是一段长度为100 cm的洋白蜡树干表面重建的效果,图 7是一段长度为50 cm的大叶白蜡树干表面重建的效果。从重建的树干表面上可以清楚地看出外业扫描时标注的树号(图 5b)、彩色粉笔标注的围尺测量直径的轨迹(图 6b),特别是大叶白蜡的凹陷部位(图 7b)。整体重建效果与数码照片接近度较高,可以依据色彩标识明确判定树干表面的方位(图 5d、图 6d)。图 5c所示局部表面上有一些小黑点,对应放大图如5d所示,这是内嵌的几个三角形构成的局部表面。图 6c能清晰地分辨不同颜色纸条所在的区域,图 6d是6c中一个黄色纸条位置处的表面三角面片,中间区域黄色三角形较多。图 7c中能清晰地看出重建表面的凹陷区域,图 7d是7c中凹陷区域边缘的三角面片,可以看出树干表面从正常区域向凹陷区域过渡到三角面片。

|
图 5 一段杨树树干点云及其重建的表面 Fig.5 A part of Populussp. stem point cloud and reconstructed surface a.外业扫描时照片Picture of the field working; b.重建的表面Reconstructed surface; c.局部表面Partial reconstructed surface; d.表面三角面片Triangular patch of reconstructed surface.下同The same below. |
|
图 6 一段洋白蜡树干点云及其重建的表面 Fig.6 A part of Fraxinus pennsylvanica stem point cloud and reconstructed surface |
从表面重建效果来看,无论是整体、局部还是表面的三角面片,重建的三角形表面模型都能清晰地看出树干表面褶皱的纹理、凸凹不平的特征及三角面片的朝向。
图 5、图 6与图 7所示的3个树种中,洋白蜡树皮最粗糙,杨树次之,大叶白蜡树皮最光滑。可以看出,无论是粗糙还是平滑树皮,重建的树干表面均能呈现出与外业时照片相类似的树干表面特征,是树干表面真实特征的体现,充分表明了改进的树干表面重建算法对树皮粗糙程度的适应性。

|
图 7 一段大叶白蜡树干点云及其重建的表面 Fig.7 A part of Fraxinus chinensisvar.rhynchophylla stem point cloud and reconstructed surface |
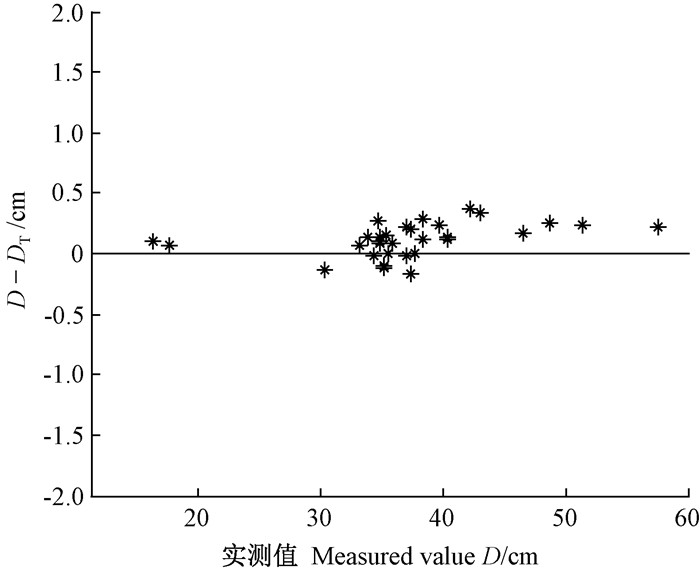
根据第2次外业围尺实测的31条围尺轨迹,得到重建表面上与之对应的31条直径数据,如表 2所示。其中编号是树木的临时编号,高度是围尺测径时树木所在的高度(006是一段原木段,测量直径时未测量高度),D是围尺实测直径,DT是从基于切平面投影重建表面上提取的直径。实测直径D与DT差值如图 8所示。
|
|
从图 8可以看出,围尺实测直径与从重建表面上提取直径的差值沿零值线水平分布,且差值不超过0.5 cm。根据评价指标,与围尺实测直径相比,从重建表面上提取直径的MAPE为0.40%,RMSE为0.18 cm。这说明了重建表面模型的精确性,同时也表明了从树干的重建表面提取树干参数的可行性与准确性。
|
图 8 从重建表面上提取直径与实测直径的差值 Fig.8 The diameter differences between extracting from reconstructed surface and field measurement |
值得注意的是,这些直径数据分别来自不同树种与不同高度处的直径数据,也进一步表明了重建算法对树皮粗糙程度的适应性。
3 讨论预处理中包括移除的噪声点处理,但这一步骤并不能准确、有效地移除所有噪声点。事实上,树干表面的粗糙性导致很难准确判定树干点云中的离散噪声点。在图 5c数字5的左上部位,可看到零星的几个白色三角形在绿色的树干表面之上,是未移除的离散噪声点形成的三角形。这类噪声点主要来源于点云配准中产生的误差,它们紧贴着树干表面,位于多站扫描时的多站相结合部位,且沿着一侧垂直分布,随着树高增高而增多。因这些离散噪声点紧贴着树干表面分布,基于距离统计或密度的离散噪声点算法很难对其准确识别。为减少此类噪声点,或提高扫描精度、在无风的天气下扫描,或进一步研究配准算法及去噪算法以提高配准精度及噪声点的判定精度。
本研究给出了改进算法的参数默认值,在不同的扫描设备及扫描精度下,可根据具体的点云密度调整算法的参数值以适应重建表面精度的需要。根据点云密度自动获取合适的参数值也是值得进一步深入研究的内容。
4 结论本研究将基于切平面投影的表面重建算法应用于树干的三维表面重建,根据树干点云特征改进了算法的具体实现内容。对比试验表明,改进算法能更好地展示树干表面的特征;在不同树种的树干表面重建试验表明,改进算法能较好地反映树干表面的凸凹褶皱特征;与围尺实测直径相比,从重建表面上提取树干直径的RMSE为0.18 cm,验证了树干重建表面的精确性。本研究改进的基于切平面投影点三维表面重建算法可适用于树干的精细可视化建模及树干的参数提取。
| [] |
高士增, 张怀清, 刘闽, 等. 2013. 树木枝干Delaunay三角网格构建技术. 西南林业大学学报 , 33 (3) : 62–68.
( Gao S Z, Zhang H Q, Liu M, et al.2013. Constructing technology of tree branches Delaunay triangulation. Journal of Southwest Forestry University , 33 (3) : 62–68. [in Chinese] ) |
| [] |
黄洪宇, 陈崇成, 邹杰, 等. 2013. 基于地面激光雷达点云数据的单木三维建模综述. 林业科学 , 49 (4) : 123–130.
( Huang H Y, Chen C C, Zou J, et al.2013. Tree geometrical 3D modeling from terrestrial laser scanned point clouds: a review. Scientia Silvae Sicicae , 49 (4) : 123–130. [in Chinese] ) |
| [] |
王晓辉, 黄洪宇, 陈崇成, 等. 2014. 基于激光点云的树木三维几何建模系统的设计与实现. 福州大学学报:自然科学版 , 42 (5) : 705–712.
( Wang X H, Huang H Y, Chen C C, et al.2014. Design and implementation of 3D geometrucal tree modeling system based on terrestrial laser scanned point cloud data. Journal of Fuzhou University:Natural Science Edition , 42 (5) : 705–712. [in Chinese] ) |
| [] |
尤承业. 2004. 解析几何. 北京: 北京大学出版社 .
( You C Y. 2004. Analytic geometry. Beijing: Beijing University Press . [in Chinese] ) |
| [] |
尤磊, 唐守正, 宋新宇. 2016. 以优先点为中心的Delaunay三角网生长算法. 中国图象图形学报 , 21 (1) : 60–68.
( You L, Tang S Z, Song X Y.2016. Growth algorithm centered on priority for constructing the Delaunay triangulation. Journal of Image and Graohics , 21 (1) : 60–68. [in Chinese] ) |
| [] |
袁方, 唐杰, 武港山. 2011. 一种基于三维Delaunay三角化的曲面重建算法. 计算机技术与发展 , 21 (10) : 14–18.
( Yuan F, Tang J, Wu G S.2011. A geometric spread approach of 3-D reconstruction. Computer Technology and Development , 21 (10) : 14–18. [in Chinese] ) |
| [] |
张剑清, 李彩林, 郭宝云. 2011. 基于切平面投影的散乱数据点快速曲面重建算法. 武汉大学学报:信息科学版 , 36 (7) : 757–762.
( Zhang J Q, Li C L, Guo B Y.2011. A fast surface reconstruction algorithm for unorganized points based on tagent plane projection. Geomatics and Information Science of Wuhan University , 36 (7) : 757–762. [in Chinese] ) |
| [] |
朱德海. 2012. 点云库PCL学习教程. 北京: 北京航空航天大学出版社 .
( Zhu D H. 2012. Point cloud library PCL. Beijing: Beihang University Press . [in Chinese] ) |
| [] | Cheng Z, Zhang X, Fourcaud T.2006. Tree skeleton extraction from a single range image//Plant Growth Modeling and Applications. Second International Symposium on IEEE : 274–281. |
| [] | De Berg M, Van Krevedl M, Overmars M, et al. 2009. Computational geometry: algorithms and applications. 3rd ed. New York:Springer-Cerlag. |
| [] | Gopi M, Krishnan S, Silva C T.2000. Surface reconstruction based on lower dimensional localized Delaunay triangulation. Computer Graphics Forum , 19 (3) : 467–478. DOI:10.1111/1467-8659.00439 |
| [] | Gorte B, Pfeifer N.2004a. Structuring laser-scanned trees using 3D mathematical morphology. International Archives of Photogrammetry and Remote Sensing , 35 (B5) : 929–933. |
| [] | Gorte B, Winterhalder D.2004b. Reconstruction of laser-scanned trees using filter operations in the 3D raster domain. International Archives of Photogrammetry, Remote Sensing and Spatial Information Sciences , 36 (Part 8) : W2. |
| [] | Hackenberg J, Spiecker H, Calders K, et al.2015. SimpleTree-an efficient open source tool to build tree models from TLS clouds. Forests , 6 (11) : 4245–4294. |
| [] | Pfeifer N, Gorte B, Winterhalder D.2004a. Automatic reconstruction of single trees from terrestrial laser scanner data. Proceedings of 20th ISPRS Congress : 114–119. |
| [] | Pfeifer N, Winterhalder D.2004b. Modelling of tree cross sections from terrestrial laser scanning data with free-form curves. International Archives of Photogrammetry, Remote Sensing and Spatial Information Sciences , 36 (Part 8) : W2. |
| [] | Rusu R B, Cousins S.2011. 3D is here: point cloud library (PCL)//Robotics and automation (ICRA). 2011 IEEE International Conference on IEEE, 1-4. |
| [] | Xu H, Gossett N, Chen B.2007. Knowledge and heuristic-based modeling of laser-scanned trees. ACM Transactions on Graphics (TOG) , 26 (4) : 19. DOI:10.1145/1289603 |
 2016, Vol. 52
2016, Vol. 52

