非线性混合效应模型(non-linear mixed effects, NLME)中，包括固定效应参数和随机效应参数，适于分析重复观测数据和纵向数据。由于NLME模型参数可以随研究对象变化而随机变化，在林业中得到了越来越广泛的应用(Lappi et al., 1988；Fang et al., 2001；Calegario et al., 2005；李永慈等，2004；李春明等，2010；姜立春等，2011；符利勇等，2012；2013)。

拟合非线性混合效应模型时，一般需要采用一阶泰勒级数将模型线性化，然后再用迭代算法确定极大似然函数并求解(Davidian et al., 1993；1995)。在线性化时，既可以用随机效应参数的数学期望为线性化的基点，亦即0值点，也可以用随机效应参数在迭代过程中的迭代值为基点。在常用的统计软件中，R和S+以0值为基点，而SAS软件以迭代终值为基点。研究表明，以迭代终值为基点的参数估计值优于以0值为基点，但需要更多的计算时间，而且往往不稳定(Lindstrom et al., 1990；Wolfinger et al., 1997)。

混合效应参数模型可用于分析不同来源的随机效应参数对应变量的影响程度；且在获得一个研究对象的若干观测值后，混合效应参数模型更可以用于预测。采用非线性混合效应参数模型进行预测时，需要2步：根据已经取得的观测值向量预测随机效应参数值；在确定了一个研究对象的随机效应值后，可以进一步预测应变量的其他观测值。随机效应参数的预测方法一般称之为经验线性无偏最优估计，简称为EBLUP(empirical best linear unbiased predictor)。与拟合类似，EBLUP同样涉及利用一阶泰勒近似将非线性模型线性化的过程，线性化基点同样可为0值或迭代终值。线性化基点不同，也导致了不同的应变量预测方法。

基于线性化基点角度，从模型拟合、随机效应参数预测到应变量预测，形成了多种组合。本文重点研究各种组合对应变量预测精度的影响。

1 材料与方法 1.1 数据

本文数据来源于加拿大哥伦比亚省(British Columbia)美国黄松(Pinus ponderosa)林分的临时样地数据。哥伦比亚省林业局于2000和2001年建立了100块临时样地，样地设置时充分考虑了现有林分的立地质量、年龄、密度以及物种丰富度等因素，本文从中选取具有代表性的林分作为样地。样地形状为圆形，面积为0.01 hm^-2(半径5.64 m)。每块样地挑选1株未受损或未受压的健康优势木或亚优势木作为样木，最终得到79株优势木的解析木。样木伐倒后，对于树桩和树干部分采取纵切的方法，由髓心直接查出树高-年龄值；对于不适合做纵切的树梢部分采取轮生枝法确定每年的树高生长量，可以精确得到每年的树高值。这种获得树高年龄数据的方法，其精确性远远高于截取圆盘进行树干解析的方法。本文随机选取49株优势木进行拟合，30株优势木进行预测，数据的详细介绍见文献(Nigh，2004)。

1.2 树高生长模型的选择与建立

林分优势树高生长模型的种类很多，主要有Logistic，Mitscherlich，Gompertz，Weibull，Richards和Korf方程等，但广泛应用的有Richards-Chapman，Logistic，Weibull和Korf方程，其模型结构见表 1。

1.3 随机效应参数预测和观测值预测

非线性混合参数模型可一般性地表示如式(1)：

$ {{y}_{i}}=f\left( {{A}_{i}}\beta +{{B}_{i}}{{b}_{i}},{{x}_{i}} \right)+{{e}_{i}}。 $

(1)

式中：y_i为第i个研究对象的应变量向量；β为p维固定效应参数向量；b_i为q维随机效应参数向量，且有b_i~N(0, D)，D为随机效应间的协方差矩阵；A_i和B_i为具有适当维数的关联矩阵(即由0或1构成的矩阵)；x_i为自变量矩阵；e_i为与y_i相关联的随机误差项向量，e_i~N(0, R_i)，R_i为随机误差项间的协方差矩阵。一般假设b_i和e_i相互独立。模型中需要估计的参数分别为β，D和R_i。需要注意，R_i一般可用方差函数和相关系数函数表示。

以b_i=b₀为基点，可将式(1)通过一阶泰勒近似表示为式(2)：

$ {{y}_{i}}\approx f\left( {{A}_{i}}\beta +{{B}_{i}}{{b}_{0}},{{x}_{i}} \right)+{{Z}_{i}}\left( {{b}_{i}}-{{b}_{0}} \right)+{{e}_{i}}。 $

(2)

式中：Z_i为式(1)关于b_i的偏导数向量，为自变量x_i的函数，形式如式(3)：

$ {{Z}_{i}}=\frac{\partial f\left( {{A}_{i}}\beta +{{B}_{i}}{{b}_{i}},{{x}_{i}} \right)}{\partial {{b}_{i}}}\left| _{\left( {{b}_{i}}={{b}_{0}} \right)} \right.。 $

(3)

式(3)中随机变量包括b_i和e_i 2个向量以及二者的线性函数y_i。由于b_i和e_i相互独立，从式(3)可有：

$ \begin{align} & \text{Cov}\left( {{y}_{i}} \right)={{Z}_{i}}DZ_{i}^{\text{t}}+{{R}_{i}}; \\ & \ \ \ \ \text{Cov}\left( {{b}_{i}},{{y}_{i}} \right)=DZ_{i}^{\text{t}}。 \\ \end{align} $

上式中上标t为矩阵转置运算符。随机向量b_i和y_i的联合分布为：

$ \begin{array}{l} \left( \begin{array}{l} {b_i}\\ {y_i} \end{array} \right) \sim N\left[ {\left( {\mathop {f\left( {{A_i}\beta + {B_i}{b_0},{x_i}} \right) - {Z_i}{b_0}}\limits^0 } \right)} \right.,\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\left. {\left( {\begin{array}{*{20}{c}} D&{DZ_i^{\rm{t}}}\\ {{Z_i}{D^{\rm{t}}}}&{{Z_i}DZ_i^{\rm{t}}{R_i}} \end{array}} \right)} \right]. \end{array} $

(4)

对于总体中的第i个研究对象，有2个应变量向量y_i(1)和y_i(2)，分别对应于x_i(1)和x_i(2)。如下将以y_i(1)为基础求出随机效应b_i的预测值${{\hat{b}}_{i}}$，然后再以${{\hat{b}}_{i}}$和x_i(2)为基础，给出y_i(2)的预测值${{\hat{y}}_{i\left(2 \right)}}$。

根据多元正态分布理论，当y_i=y_i(1)时，从式(4)可以得出b_i的条件分布数学期望为式(5)，其中E(b_i)=0。统计上，一般以数学期望预测随机变量的取值，因而随机变量b_i在y_i=y_i(1)时的预测值可表示为式(6)：

$ \begin{align} & \text{E}\left( {{b}_{i}}\left| _{{{y}_{i}}={{y}_{i}}\left( 1 \right)} \right. \right)=\text{E}\left( {{b}_{i}} \right)+DZ_{i\left( 1 \right)}^{\text{t}}{{\left( {{Z}_{i\left( 1 \right)}}DZ_{i\left( 1 \right)}^{\text{t}}+{{R}_{i}} \right)}^{-1}} \\ & \ \ \ \ \ \ \ \ \ \left[ {{y}_{i\left( 1 \right)}}-f\left( {{A}_{i}}\beta +{{B}_{i}}{{b}_{0}},{{x}_{i\left( 1 \right)}} \right)+{{Z}_{i\left( 1 \right)}}{{b}_{0}} \right]; \\ \end{align} $

(5)

$ \begin{align} & {{{\hat{b}}}_{i}}=DZ_{i\left( 1 \right)}^{\text{t}}{{\left( {{Z}_{i\left( 1 \right)}}DZ_{i\left( 1 \right)}^{\text{t}}+{{R}_{i}} \right)}^{-1}}\left[ {{y}_{i\left( 1 \right)}}- \right. \\ & \ \ \ \ \ \ \left. f\left( {{A}_{i}}\beta +{{B}_{i}}{{b}_{0}},{{x}_{i\left( 1 \right)}} \right)+{{Z}_{i\left( 1 \right)}}{{b}_{0}} \right]。 \\ \end{align} $

(6)

由式(6)可知，在已获得β，D和R_i估计值的前提下，给定一个基点b₀值，就可以求出相应的${{\hat{b}}_{i}}$。不同的b₀值会在一定程度上导致${{\hat{b}}_{i}}$值的变化。一阶泰勒近似精度与基点选择有关，如果以式(6)求出的${{\hat{b}}_{i}}$值作为基点，则利用式(6)可进一步改进b_i估计值。反复利用式(6)，可形成逐步改进${{\hat{b}}_{i}}$值的迭代过程。以第k次迭代的b_i预测值${{\hat{b}}_{i\left(k \right)}}$为基点(k=0, 1, 2，…)，第k+1次迭代的b_i预测值${{\hat{b}}_{i\left(k+1 \right)}}$则可表示为式(7)。${{\hat{Z}}_{i\left(1 \right)}}$可通过令式(3)中的x_i=x_i(1)，β=$\hat{\beta }$求出。

$ \begin{align} & {{{\hat{b}}}_{i\left( k+1 \right)}}=\hat{D}\hat{Z}_{i\left( 1 \right)}^{\text{t}}{{\left( {{{\hat{Z}}}_{i\left( 1 \right)}}\hat{D}\hat{Z}_{i\left( 1 \right)}^{\text{t}}+{{{\hat{R}}}_{i}} \right)}^{-1}} \\ & \left[ {{y}_{i\left( 1 \right)}}-f\left( {{A}_{i}}\hat{\beta }+{{B}_{i}}{{b}_{i\left( k \right)}},{{x}_{i\left( 1 \right)}} \right)+{{{\hat{Z}}}_{i\left( 1 \right)}}{{b}_{i\left( k \right)}} \right]。 \\ \end{align} $

(7)

当$\left| {{{\hat b}_{i\left( {k + 1} \right)}} - {{\hat b}_{i\left( {k + 1} \right)}}} \right| < \varepsilon $时，即当${{{\hat{b}}}_{i\left(k \right)}}$和${{{\hat{b}}}_{i\left(k+1 \right)}}$的差值小于预先指定的很小正数ε时，二者近似相等，表示已无改进余地，此时式(6)中的b₀=${{{\hat{b}}}_{i\left(k \right)}}$，b_i=${{{\hat{b}}}_{i\left(k+1 \right)}}$。令b₀=${{{\hat{b}}}_{i\left(k \right)}}$，b_i=${{{\hat{b}}}_{i\left(k+1 \right)}}$，x_i=x_i(2)，可由式(2)得出${{{\hat{y}}}_{i\left(2 \right)}}$，表示如式(8)。忽略${{{\hat{b}}}_{i\left(k \right)}}$和${{{\hat{b}}}_{i\left(k+1 \right)}}$间的差异，式(8)中的${{Z}_{i}}\left({{{\hat{b}}}_{i\left(k+1 \right)}}-{{{\hat{b}}}_{i\left(k \right)}} \right)\approx 0$，并将${{{\hat{b}}}_{i\left(k+1 \right)}}$一般性地表示为${{{\hat{b}}}_{i}}$，式(8)可表示为式(9)：

$ \begin{align} & {{{\hat{y}}}_{i\left( 2 \right)}}\approx f\left( {{A}_{i}}\hat{\beta }+{{B}_{i}}{{b}_{i\left( k \right)}},{{x}_{i\left( 2 \right)}} \right)+ \\ & \ \ \ \ \ \ {{{\hat{Z}}}_{i\left( 2 \right)}}\left( {{{\hat{b}}}_{i\left( k+1 \right)}}-{{{\hat{b}}}_{i\left( k \right)}} \right); \\ \end{align} $

(8)

$ {{{\hat{y}}}_{i\left( 2 \right)}}\approx f\left( {{A}_{i}}\hat{\beta }+{{B}_{i}}{{b}_{i\left( k \right)}},{{x}_{i\left( 2 \right)}} \right)。 $

(9)

在迭代过程中，一般基点的迭代初值取0。如果不继续迭代，那么b₀=0，式(2)和(6)则分别变为式(10)和(11)。与式(10)相对应地将${{{\hat{y}}}_{i\left(2 \right)}}$表达为式(12)：

$ {{y}_{i}}\approx f\left( {{A}_{i}}\beta ,{{x}_{i\left( 1 \right)}} \right)+{{Z}_{i}}{{b}_{i}}+{{e}_{i}}; $

(10)

$ \begin{align} & {{{\hat{b}}}_{i}}=\hat{D}\hat{Z}_{i\left( 1 \right)}^{\text{t}}{{\left( {{{\hat{Z}}}_{i\left( 1 \right)}}\hat{D}\hat{Z}_{i\left( 1 \right)}^{\text{t}}+{{{\hat{R}}}_{i}} \right)}^{-1}} \\ & \ \ \ \ \ \left[ {{y}_{i\left( 1 \right)}}-f\left( {{A}_{i}}\hat{\beta },{{x}_{i\left( 1 \right)}} \right) \right]; \\ \end{align} $

(11)

$ {{{\hat{y}}}_{i\left( 2 \right)}}\approx f\left( {{A}_{i}}\hat{\beta },{{x}_{i\left( 2 \right)}} \right)+{{{\hat{Z}}}_{i\left( 2 \right)}}{{{\hat{b}}}_{i}}。 $

(12)

给定一个研究对象，如果已经获得了观测值向量y_i(1)，则可以用式(7)通过迭代求出b_i的预测值，也可以用式(11)直接求出b_i的预测值${{{\hat{b}}}_{i}}$，区别在于一阶泰勒近似的基点不同。获取${{{\hat{b}}}_{i}}$值后，对y_i(2)的预测可用式(9)或(12)。从以上分析可知，式(7)和(9)自然地联系起来，而式(11)和(12)也同样如此。

式(9)对于${{{\hat{b}}}_{i}}$而言是非线性的，而式(12)则为线性的。为后续讨论描述简洁，将式(9)和(12)分别称为非线性预测和线性预测。在林业中，用式(11)预测随机效应的应用更多一些(Fang et al., 2001；Hall et al., 2001；Calama et al., 2004；Sharma et al., 2007；2009；Temesgen et al., 2008；Huang et al., 2009b；Jiang et al., 2010；祖笑锋等，2015)，利用式(7)的也有(Hall et al., 2004；Meng et al., 2009；Huang et al., 2009a；Ni et al., 2012；Yang et al., 2013)。

从模型拟合、随机效应参数预测和应变量y_i(2)的预测，每个环节都包含了2种方法，共计形成8种组合，本文重点研究各种组合对应变量预测精度的影响。当基点b₀=b^_i且b^_i接近于b_i的真值时，由于泰勒近似在基点附近的近似效果较好，式(2)对模型(1)的近似效果要优于式(10)。同样由于近似基点不同的原因，相对应地，式(7)对b_i的预测效果也应该优于式(11)。直观上，均以迭代终值为基点的模型拟合(SAS的nlmixed过程)、随机效应预测[式(7)]、相关联的应变量预测[式(9)]，此组合应优于其他任何组合。事实是否如此，为本文的研究目的之一。

虽然式(7)与(9)之间以及式(11)和(12)之间存在承接关系，但在林业上却多采用式(11)预测随机效应参数，采用式(9)预测y_i(2)(Fang et al., 2001；Sharma et al., 2007；2009；Jiang et al., 2010)。此种组合对预测精度影响如何，也是本文的研究目的之一。

本文采用3种预测精度评价指标，其定义如表 2。3种评价指标值越小，表明预测精度越高，其最优值都为0。

2 结果与分析 2.1 树高生长模型的比较

采用以上4个生长模型作为基本模型，利用R软件的nlme过程对49株解析木进行拟合，其统计量见表 3。

使用AIC，BIC和Loglik 3个模型评价指标对拟合结果进行评价。由表 3可知，Logistic方程的AIC，BIC最小且logLik最大，表明Logistic方程拟合效果最好，因此将其作为混合效应模型的基本模型。

2.2 拟合非线性混合效应模型

在林业中，广泛应用Logistic方程分析优势木树高生长与年龄的关系。采用三参数Logistic非线性混合效应模型具有相当大的灵活性，Logistic模型如式(13)：

$ {{y}_{i,j}}=\frac{{{\beta }_{1}}}{1+{{e}^{{{\beta }_{2}}+{{\beta }_{3}}\ln \left( {{x}_{i,j}} \right)}}}+{{e}_{i,j}}。 $

(13)

若将模型中的3个参数都处理为混合参数，如式(14)(Calegario et al., 2005)：

$ {{y}_{i,j}}=\frac{{{\beta }_{1}}+{{b}_{1,i}}}{1+{{e}^{\left( {{\beta }_{2}}+{{b}_{2,i}} \right)+\left( {{\beta }_{3}}+{{b}_{3,i}} \right)\ln \left( {{x}_{i,j}} \right)}}}+{{e}_{i,j}}。 $

(14)

式中：y_{i, j}表示第i个林分在年龄x_{i, j}时的树高；β₁, β₂, β₃为方程的固定效应参数；与之相对应的随机效应参数分别为b_{i, 1}，b_{i, 2}，b_{i, 3}；e_{i, j}为方程误差项，且与b_{i, 1}，b_{i, 2}，b_{i, 3}任何一个均相互独立。

随机抽取49株解析木用于模型拟合，采用R语言的nlme函数和SAS的nlmixed过程进行拟合，分别对应于以0值为基点和以迭代终值为基点的拟合方法。参数估计值如表 4所示，其中${{{\hat{\beta }}}_{1}}$, ${{{\hat{\beta }}}_{2}}$, ${{{\hat{\beta }}}_{3}}$为固定效应参数估计值；随机效应参数协方差矩阵估计值${\hat{D}}$为三维对称矩阵；${{{\hat{\sigma }}}^{2}}$为随机误差项估计值。以上参数主要用于计算新个体的随机效应参数值。

2.3 预测精度分析

本文对30株验证数据设置了不同的起始年龄和间隔，从多角度评价预测优势木树高生长精度。在表 5中，字母组合代码的第1位代表预测随机效应参数的线性化方法，Z值表示以期望值(0值)为线性化基点，而E值则代表以迭代终值为基点；第2位代表应变量预测方法，N表示非线性预测，L表示线性预测。表中的年龄值为观测值y_i(1)对应的年龄值，预测应变量y_i(2)为其后面连续5年的观测值。如以第(1)行中30, 31, 32, 33, 34作为观测值，预测35, 36, 37, 38, 39年的优势木树高值。8种组合均计算了MSPE，MPE以及MAPE。

从列于表 5的结果可见，无论模型拟合以0值为基点还是以迭代终值为基点，ZL组合在2种模型拟合方法中的表现大致相同，EN组合也是如此，与模型拟合方法无关，ZL和EN组合总是明显地优于ZN和EL组合。根据表 5中的组合代码定义，EN组合对应于式(7)与(9)，而ZL组合对应于式(11)和(12)。表 5预测精度表明，随机效应预测方法决定了应变量的预测方法。拟合模型(10)对应于用模型(11)计算b_i值，在模型预测时自然应该以模型(10)为基础，对应的模型预测公式则为式(12);同理，拟合模型(2)对应于用模型(7)计算b_i值，自然以式(2)为基础，并由式(2)进一步导向了式(9)。因而，式(7)与(9)以及式(11)与(12)之间必须配合使用，而与模型拟合方法的关系不大。

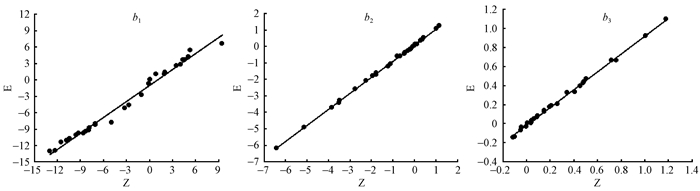
2.4 单株解析木示例 2.4.1 随机效应参数预测分析

为分析基于0值和迭代终值的2种线性化方法对随机效应参数预测的影响，对同一解析木，在x_i(1)相同的前提下，分别用2种方法获取随机效应参数预测值，共计有30株解析木的30对预测值，二者对比结果如图 1所示。基于0值和迭代终值的2种线性化方法预测随机效应参数的结果基本上一致，说明式(2)和(10)对模型(1)的近似效果对大多数解析木而言非常接近，表明多数解析木的b_i位于其期望值附近。

2.4.2 应变量预测结果分析

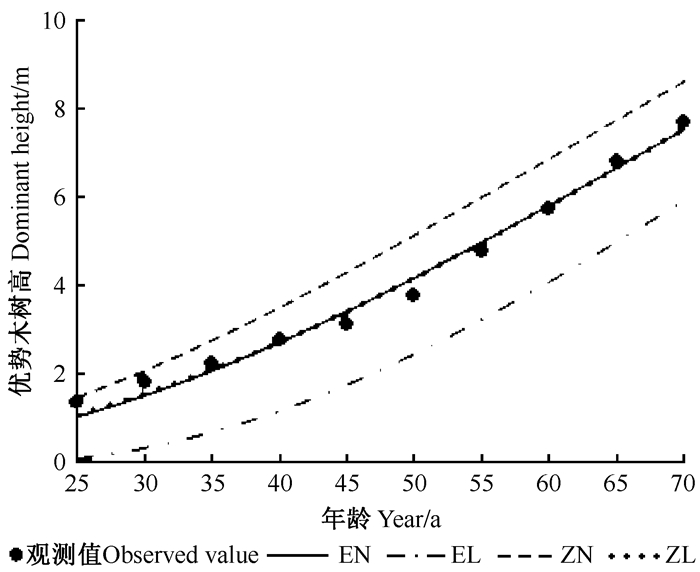
为分析随机效应和应变量预测间各种组合对预测结果的影响，本文选取1株解析木，用4种不同组合进行匹配验证，结果如图 2所示。从图 2可见，ZL和EN组合几乎完全重合，并且均能紧密跟踪数据散点；与此相反，ZN和EL组合则均明显地偏离数据散点。

以ZN和ZL组合为例，由于模拟拟合和随机效应参数的预测方法完全一致，二者的所有参数估计值均相同，唯有预测y_i(2)的模型不同，分别为式(9)和(12)。ZN和ZL组合曲线间的差异，完全由式(9)和(12)间差异所致。

ZN组合，亦即式(13)与(11)搭配使用，在林业中误用较多。由表 5可知，ZN组合与ZL和EN组合相比，其预测精度急剧下降；且ZL组合预测精度略微优于EN组合，但尚不足以得出ZL优于EN的结论，可认为二者预测精度处于同一量级水平。但从应用方便角度看，式(9)有时无法收敛，而不能求出b_i值，因而ZL组合优于EN组合。

在表 5中，第(1)行观测间隔为1年，而(2)~(10)行观测间隔为2年，其目的是预测不同年龄段内MSPE，MPE以及MAPE的变化。对于正确的匹配方法，MSPE，MPE和MAPE 3种评价指标值表现得都很稳定，且明显小于错误匹配。但特别强调的是第(11)~(14)行，观测数目相同，观测间隔不同，随着观测间隔增加，3种评价指标的预测精度均有所提升。

3 结论与讨论

本文从线性化基点角度出发，分析了NLME模型拟合、随机效应参数预测以及应变量预测间多种线性化基点组合对应变量预测精度的影响，并以MSPE，MPE和MAPE 3种指标作为预测精度评价指标进行讨论。从所用数据和模型角度看，经验性分析结果表明，模型拟合与随机效应参数预测方法间线性化基点一致与否对预测精度的影响非常有限；与此相反，如果随机效应参数预测和应变量预测间线性化基点不同，将极为显著地降低应变量的预测精度。

混合效应模型拟合和随机效应参数预测可以视为2个不同的拟合阶段，分别对于总体特征和1个特定个体。混合效应参数模型拟合为第1阶段，其目的在于获取总体特征参数，如总体参数β，D以及与R_i相关联的方差函数和自相关函数的参数估计值。结果表明，以迭代终值为基点优于以0值为基点的参数估计值(Lindstrom et al., 1990；Wolfinger et al., 1997)。第2阶段拟合，即在已经获得总体参数估计值的前提下，对1个特定研究对象进行再次拟合，获取其对应的随机效应参数b_i值，并直接应用于此特定个体的应变量预测。除总体参数β估计值外，D和R_i的估计值仅通过影响b_i值而间接影响应变量的预测。结果表明，这种总体参数对应变量预测的间接作用，在第2阶段拟合时已极大的弱化。

经验性分析结果表明，模型拟合、随机效应参数预测和应变量预测三者间线性化基点完全一致，与仅仅后二者相一致的预测精度相比，并无任何明显优势(参考表 5)；与此相反，如果模型拟合和随机效应预测的线性化基点一致，同一个体的所有参数估计值均一致，但在预测应变量时，不同基点的预测精度却完全不同(参考图 2)。这一结果表明，线性化基点不同有时导致了近似程度差异较大，二者间的差异程度取决于b_i值与期望值的差异程度。这种差异存在于模拟拟合、随机效应预测和应变量预测中任何二者之间，但对应变量预测精度的影响却截然不同。随机效应参数预测和应变量预测间线性化基点不一致，更为直接和显著地影响应变量预测精度，而模型拟合和随机效应间的不一致，则基本上微乎其微。

从应变量预测角度看，随机效应参数预测和应变量预测间线性化基点一致更为重要。在预测随机效应时，虽然以迭代终值为基点可能获取更为精确的预测值，但在迭代运算时有时无法收敛，而以0点为基点总能给出随机效应的预测值，因而建议使用0值为基点[(式11)]预测随机效应，并以与之相对应的应变量线性预测[(式12)]进行应变量预测。在林业中，以0值为基点预测随机效应却配以不相应的非线性预测[(式12)]的组合应用较多，对此组合对应变量预测精度的影响，尚未引起足够的重视。