文章信息
- 林卓, 吴承祯, 洪伟, 洪滔
- Lin Zhuo, Wu Chengzhen, Hong Wei, Hong Tao
- 杉木人工林碳汇木材复合经济收益分析及最优轮伐期确定--基于时间序列预测模型
- Economic Benefits Analysis of Carbon Sequestration and Timber and Determination of Optimal Rotation Period for a Cunninghamia lanceolata Plantation--Based on Time Series Model
- 林业科学, 2016, 52(10): 134-145
- Scientia Silvae Sinicae, 2016, 52(10): 134-145.
- DOI: 10.11707/j.1001-7488.20161017
-
文章历史
- 收稿日期:2015-08-13
- 修回日期:2016-01-07
-
作者相关文章
2. 福建省科学技术信息研究所 福州 350003;
3. 武夷学院生态与资源工程学院 武夷山 354300
2. Fujian Institute of Scientific and Technological Information Fuzhou 350003 ;
3. Department of Ecology and Resource Engineering, Wuyi University Wuyishan 354300
随着全球经济的快速发展,大气中二氧化碳(CO2)等温室气体浓度上升导致全球气候变化问题已引起世界各国的重点关注。森林在生长过程中能吸收大量的CO2,以生物量的形式固定在植物体和土壤中,森林生态系统是陆地生态系统中最重要的碳库(Dixon et al., 1994)。发展森林碳汇不仅潜力巨大,而且具有明显的成本优势,是缓解全球变暖的重要途径(Pan et al., 2011)。积极开展森林碳汇活动,在改善生态环境的同时,还能促进林业收入的增长,因此森林碳汇价值越来越受到重视(李怒云等,2006)。森林碳汇价值的实现,为森林碳汇交易的发展提供了机会,同时也会对森林经营产生影响,在考虑碳汇价值情况下,可能会使原来的经营成本、经济收益和经营决策发生变化,但在现有森林经营环境下,只有获得额外的经济收益才会激励森林经营者转变经营方式,丰富森林经营目标(Fahey et al., 2009;王枫等,2012)。欧美等发达国家对森林碳汇价值融入森林最优轮伐期确定的研究已有一定的积累,利用各种方法和模型探索森林资源最优利用经营方案(Diaz-Balteiro et al., 2006;Guthrie et al., 2009;Asante et al., 2011)。国内对森林碳汇价值影响经营主体的研究起步较晚,虽然在探讨森林碳汇价值对营林经济收益影响等领域已有相关报道(陈冲影,2010;简盖元等,2011;于金娜等,2012),但研究成果多侧重于理论分析碳汇价值带来的变化,缺乏碳交易情景下对林分经济收益的变化研究,而基于实地案例的碳汇木材复合经营目标下经济收益及影响因素的相关研究更是相对较少(任腾腾等,2013)。
南方集体林区是我国三大林区中森林面积最大的林区,优越的自然条件适合林木快速生长,具有较大的森林碳汇潜在优势(沈月琴等,2013a)。随着南方集体林权改革,林农成为南方集体林区森林经营主体,对农户而言,追求森林经济收益最大化是其最主要的经营目标。当增加森林碳汇经营目标后,生产要素的投入及产出都会发生变化,因而会影响资金的时间价值,进一步对最佳经营决策产生影响(朱臻等,2013a)。杉木(Cunninghamia lanceolata)作为南方集体林区中重要的用材林树种,在我国林业发展中占有极其重要的地位,研究其碳汇价值与经济收益的关系具有一定的实践意义。任腾腾等(2013)基于浙江省实地调查数据,模拟分析碳交易情景下杉木人工林最佳轮伐期以及林地收益的变化,结果发现随着碳价格上升森林的最优轮伐期发生变化且林地效益显著增加。朱臻等(2013b)以浙江和江西2省调查的杉木人工林为对象,分析碳汇经营目标下的林地期望价值及森林经营最优决策的变化,结果发现在目前的碳汇林经营模式下,森林木材收益和碳收益经营是可协调的。沈月琴等(2013b)运用修正的Faustmann-Hartman模型分析增加碳汇收益对我国南方杉木人工林经营的影响,结果表明在考虑碳汇收益后会明显增加林地作为资产的价值,因此可能会致使其他用途的土地转化为林业用地,而最优轮伐期也随着碳汇价格的变化而变化,但对不同立地等级的林地影响程度存在差异。这些研究都以杉木实地案例为研究对象,评估了考虑碳汇价值情况下森林经营经济收益及经营决策的变化;但这些研究中对林分产出(木材产量和碳储量)估算模型的选择存在局限性,几乎全是利用前人研究的相对应区域林分理论生长模型进行蓄积量或碳储量的预测,模型形式单一且未对模型的适用性进行分析。然而在实地案例研究中,林分产出的估算是森林经济收益分析的基础,探索更加适合实际林分的预测方法,提高对林分蓄积量和碳储量的预测精度,能增加实地案例研究结果的可靠性。因此,本研究提出利用时间序列预测模型对林分蓄积量和碳储量进行预测。
时间序列预测模型常用来分析具有时间序列特性的现实数据,并进行预报和控制,其中差分自回归移动平均模型(ARIMA)是较为常用的模型之一(Box et al., 2011)。ARIMA模型已广泛应用于农业、医学、经济等领域中(王志忠等,2007;彭志行等,2008;熊志斌,2011),林分生长过程无论是蓄积量还是碳储量都构成标准的时间序列,但利用该模型对碳储量进行预测的研究鲜有报道,仅续珊珊(2011)利用ARIMA模型分析了黑龙江省森工国有林区近30年来森林乔木层碳储量的变化趋势,及权伟等(2014)以1991-2011年洞头大型藻类固碳量为基础,利用ARIMA模型对其碳汇强度进行了拟合和预测。在外界扰动相对较小的情况下,林木的生长具有一定的规律性,森林蓄积量和碳储量的增长呈现出较明显的时间序列特征,在一定时间内保持相对稳定(续珊珊,2011)。鉴于此,在林分尺度上建立相应的ARIMA模型对蓄积量和碳储量进行预测分析具有一定可行性。
本研究以杉木人工林实际调查数据为基础,首次在林分尺度上利用时间序列预测模型对现实林分的蓄积量和碳储量进行预测;同时为了更全面地分析碳汇木材复合经济收益及最优轮伐期的变化,采用年均净现值法和林地期望价法计算经济收益,并探讨了立地质量、碳价格以及利率等因素对复合经济收益及最优轮伐期的影响。试图通过案例研究,探索更具有实践操作性的预测方法及更准确的经济收益分析,为杉木经营者在碳汇交易背景下选择最优森林经营决策提供依据;同时将碳汇价值纳入经济收益进行研究,对转变森林经营方式、推动南方集体林区碳汇林业发展、实现减排目标也具有重大现实意义。
1 研究区概况研究区设在福建金森林业股份有限公司经营的杉木人工林栽培区,该区域位于福建省西北部的将乐县(117°05′-117°40′E,26°26′-27°04′N),境内地形复杂多样,地貌以低山和丘陵为主,海拔一般在800 m以下。该区域属于中亚热带季风气候,主导风向为东南风。土壤具有典型的中亚热带地带性土壤特征,林地土壤深厚,有机质含量较高,养分丰富。地带性植被属中国东部温润森林区亚热带常绿阔叶林,植被种类复杂多样,垂直分布明显。主要的杉木人工林群落有杉木-芒萁(Dicranoptens dichotoma)群落、杉木-五节芒(Miscanthus floridulus)+蕨类(Pteridum spp.)群落。
2 材料与方法 2.1 数据收集2012年在研究区内设置不同立地质量,年龄为5~26年、初植密度为3 000~3 500株·hm-2且未经大规模间伐(抚育间伐总强度不超过15%)的杉木人工林样地440块,每块样地面积600 m2。对样地进行每木检尺,调查每株林木胸径、树高及每100 m2优势木的胸径和树高,采用福建省杉木二元材积表计算每木材积并计算林分蓄积量。
为计算经济收益,参考金森林业股份有限公司2012年森林经营的实际情况,调查收集了各类相关费用,经筛选后本研究所采用的经济指标主要有:木材价格,其中规格材1 300元·m-3,非规格材1 000元·m-3;税费按木材起征价征收,其中规格材为500元·m-3,非规格材为390元·m-3;相关税费:育林费,按木材统一计征价的10%计取;森林植物检疫费,按木材销售价的2‰计取;防洪费,按木材销售价的0.7‰征收;木材采集运费用150元·hm-2;伐区设计费,按每立方米木材(出材)8元计取;木材检尺费,按每立方米木材(出材)15元计取;销售费用,按销售收入的2%提取;管理费用(含管理人员工资),按销售收入的10%提取;营林生产成本:杉木营林费用为9 000元·hm-2 (包括林地清理、整地、施肥、栽植、补植、苗木款、挖管茅、肥料苗木运输费、管理费等);年均病虫害防治费为30元·hm-2;年平均森林管护费为90元·hm-2;年均林地使用费为150元·hm-2。
2.2 研究假设研究采用时间序列模型(ARIMA)对现实林分的蓄积量和碳储量进行模拟预测。由于缺乏对固定样地的连年调查数据,故以空间代时间的方法有针对性地选取调查对象进行研究,且基于以下假设:1) 地位指数按吴承祯等(1995)提出的杉木人工林Sloboda树高生长模型进行估计,结果范围为11.81~19.72 m,故按照12~14 m,14~16 m,16~18 m,18~20 m将调查样地分为4类(分别以Ⅰ,Ⅱ,Ⅲ,Ⅳ表示),并认为每类立地中的林分具有相近的生长环境;2) 按照杉木龄组划分,通常将26年之后的林分归为成熟林,且杉木造林后郁闭时间基本上在前4年,故本研究调查对象选取林分年龄为5~26年、初植密度为3 000~3 500株·hm-2的林分。由于这些林分在后续经营中间伐总强度不超过15%,所以可以认为所调查的林分在造林结束后具有大致相同的密度,且密度变化遵循自然稀疏规律。在这些假设下,本研究调查数据可以近似看作是对固定样地的连年调查数据,符合采用时间序列模型预测的前提。
2.3 数据处理 2.3.1 碳储量计算研究对象林分涵盖幼龄林、中龄林和近熟林,所以本研究分别采用IPCC 2006推荐的生物量扩展因子法和Fang等(2001)提出的生物量转换因子连续函数法先计算杉木林分平均生物量,然后乘以杉木的平均含碳率(取0.471))得到林分碳储量,最后取二者的平均值作为样地的碳储量观测值进行模拟预测。
1) 根据国家林业局《造林项目碳汇计量与监测指南(2011年)》。
生物量扩展因子法的计算公式为:
| $ B\text{=}V\cdot \text{WD}\cdot \text{BE}{{\text{F}}_{1}}\cdot \left(1+R \right)。 $ | (1) |
式中:B为单位面积生物量(t·hm-2);V为单位面积蓄积量(m3·hm-2);WD为杉木的木材密度,取0.312)(t·m-3);BEF1为IPCC推荐的生物量扩展因子,即单位面积蓄积材积比,取1.53;R为根茎比,即地下生物量与地上生物量之比,取0.24。
2) 根据国家林业局《造林项目碳汇计量与监测指南(2011年)》。
生物量转换因子连续函数法的计算公式为:
| $ \text{BE}{{\text{F}}_{2}}=a+b/V; $ | (2) |
| $ B\text{=BE}{{\text{F}}_{2}}\cdot V=aV+b。 $ | (3) |
式中:BEF2为连续函数法计算的生物量转换因子;a,b为常数,杉木的a取0.399 9(t·m-3),b取22.541 0(t·hm-2)。
经计算后,主要测树因子分布范围为:平均胸径4.9~21 cm,平均树高4.0~17.9 m,优势高5.5~20 m,立地指数11.81~19.72 m,蓄积量16.1~406 m3·hm-2,碳储量9.73~99.42 t·hm-2。
2.3.2 林分出材率计算林分出材率的计算采用陈则生(2010)建立的杉木人工林林分材种出材率模型:
| $ {{P}_{1}}=100.8124{{\text{e}}^{-306.703/\left(D/H \right)}}, R=0.8964; $ | (4) |
| $ {{P}_{2}}=77.98864{{\text{e}}^{-0.00259\left(D/H \right)}}, R=0.8737。 $ | (5) |
式中:P1为林分规格材出材率;P2为林分非规格材出材率;D为林分平均胸径(cm);H为林分平均树高(m)。
2.3.3 碳价格计算碳价格的确定是计算碳汇经济价值的前提。Uzawa(1991)综合考虑了全球CO2变化情况和国家经济水平,提出以碳税率作为不受市场供需因素影响的理论碳价格,其计算公式为:
| $ CP=\frac{1}{p+\gamma }\cdot \frac{\beta \cdot {{A}_{t}}}{\left({{V}_{\text{g}}}-{{D}_{t}} \right)/{{N}_{t}}}。 $ | (6) |
式中:CP为理论碳价格(元·t-1);t为基期,取2012年;Nt为第t年全球人口总数,取70.9亿3);At为第t年国内居民人均纯收入,经计算取16 673.88元4);p为贴现率;γ为CO2吸收率,取0.14;β为大气CO2的敏感性系数,取0.1;Vg为大气CO2含量的临界值,取1.2 t;Dt为t时期大气CO2总储量,取8 400亿t 5)。
3) 根据美国人口调查局(United States Census Bureau)2012年统计数据。
4) 根据中华人民共和国国家统计局发布的《中华人民共和国2012年国民经济和社会发展统计公报》计算。
5) 根据世界气象组织《2012年温室气体公报》数据计算。
在我国碳交易中,往往以碳交易所的成交价作为现实市场中碳价格,历史记录显示最低值为15元·t-1、最高值为123元·t-1。
2.4 时间序列预测模型ARIMA模型的思路为先分析时间序列的随机特性,再用实际的统计序列数据构造自回归移动平均模型,并用此模型求出预测值。
2.4.1 预报模型类型在时间序列分析中,自回归模型(AR)是描述数据序列yt自身某一t时刻与前k个时间之间的相互关系,其形式为:
| $ {{y}_{t}}={{a}_{0}}+{{a}_{1}}{{y}_{t-1}}+{{a}_{2}}{{y}_{t-2}}+\cdots +{{a}_{k}}{{y}_{t-k}}+{{\varepsilon }_{t}}。 $ | (7) |
式中:a0,a1,,a2,…,ak为模型参数;εt为白噪声序列,反映了所有其他随机因素的干扰。
如果将yt看成各期随机干扰即白噪声序列的线性组合,那么就可以建立移动平均模型(MA),即每个t时间序列都是过去j个时间随机扰动项的加权平均,其一般形式为:
| $ {{y}_{t}}={{b}_{0}}+{{\varepsilon }_{t}}+{{b}_{1}}{{\varepsilon }_{t-1}}+{{b}_{2}}{{\varepsilon }_{t-2}}+\cdots +{{b}_{j}}{{\varepsilon }_{t-j}}。 $ | (8) |
式中:b0,b1,b2,…,bj为模型参数。
将AR和MA相结合构造自回归移动平均模型(ARMA),其一般形式为:
| $ \begin{matrix} {{y}_{t}}=c{{+}_{1}}{{y}_{t-1}}+{{a}_{2}}{{y}_{t-2}}+\cdots +{{a}_{k}}{{y}_{t-k}}+{{\varepsilon }_{t}}+ \\ {{b}_{1}}{{\varepsilon }_{t-1}}+{{b}_{2}}{{\varepsilon }_{t-2}}+\cdots +{{b}_{j}}{{\varepsilon }_{t-j}}.. \\ \end{matrix} $ | (9) |
式中:c为常数项。
ARMA模型在实际的时间序列分析时具有更强的代表性,AR和MA模型可以看成是ARMA(j,k)模型分别对应于j=0和k=0时的特例。
运用ARMA模型的前提是时间序列数据是平稳的,但实际中的时间序列数据往往是非平稳的,需要进行差分处理,转换为平稳序列。所以在实践中,较常用的是差分自回归移动平均模型(ARIMA),常略记为ARIMA(k,d,j),其中d为差分次数,大部分的时间序列数据都可用k,d,j不超过3的ARIMA模型来描述。
2.4.2 模型检验及评价对于建立的ARIMA预测模型,需要经过检验和评价其有效性之后才能进行模拟预报。残差序列为白噪声序列是判断模型合适的必要条件。最小信息量(AIC)准则是考察模型对原数据拟合程度的方法之一,所组建模型的AIC值越小越好。在ARIMA时间序列分析模型中,使用剩余平方和来表示模型回归效果的好坏,决定系数(R2)越大,越接近1,说明建立的预测模型拟合效果越好。
2.5 经济成熟计算本研究采用年均净现值法和林地期望价法对各林龄的林分经济收益进行计算分析1),且分别考虑了单一木材经济收益和碳汇木材复合经济收益2种情况,最优轮伐期以经济成熟龄来确定。
1) 由于选取研究林分总间伐强度不超过15%,为了简化计算,本研究木材收益仅考虑主伐时木材收入,而不考虑间伐收益。
2.5.1 年均净现值法在森林资产评估中,常用年均净现值法(average net present value, ANPV)来选择最佳采伐方案,一般认为年均净现值达到最大,即单位面积林地上平均每年收获效益最多时,林分达到了经济成熟,以该年龄来确定最优轮伐期,才能保证持续经营情况下总经济收益最大。本文年均净现值法计算公式为:
| $ \begin{matrix} \text{ANPV=}\frac{1}{t}\left\{ \frac{{{A}_{t}}-E\cdot \left[ {{\left(1+p \right)}^{t}}-1/p \right]}{{{\left(1+p \right)}^{t}}}- \right. \\ \left. K+\frac{\left(1-q \right)\cdot \text{CP}\cdot \text{CS}}{{{\left(1+p \right)}^{t}}} \right\}。 \\ \end{matrix} $ | (10) |
式中:At为第t年采伐时木材纯收入;K为造林成本;E为年森林经营管护费;p为投资收益率(即贴现率);q为林分采伐后由于各种因素导致的碳排放率,取20%(Stainback et al., 2002);CP为碳价格(元·t-1),取0时,即变为仅考虑木材收益的年均净现值;CS为第t年采伐时林分碳储量(t·hm-2)。
2.5.2 林地期望价法传统的Faustmann模型在计算林地期望值时,仅考虑木材产品的净收益现值,改进后的Hartmann-Faustmann模型(Hartman,1976)不仅能涵盖木材净收益,还将森林游憩、水源涵养等森林生态服务价值纳入其中。Richards等(2004)以此为基础将森林碳汇纳入林地期望值计算。沈月琴等(2013b)又基于前人的研究,将碳收益作为内生变量,构建出木材碳汇联合经营决策模型。结合本研究对象的实际情况,本文林地期望价法(land expectation value, LEV)计算公式为:
| $ \begin{matrix} \text{LEV=}\frac{{{A}_{t}}-K\cdot {{\left(1+p \right)}^{t}}}{{{\left(1+p \right)}^{t}}-1}- \\ \left. \frac{E}{p}+\frac{\left(1-q \right)\cdot \text{CP}\cdot \text{CS}\cdot {{\left(1+p \right)}^{t}}}{{{\left(1+p \right)}^{t}}-1} \right\}。 \\ \end{matrix} $ | (11) |
式中:各变量含义同式(10)。当林地期望价最大时,认为林分达到经济成熟,以此作为经济成熟目标下的最优轮伐期,CP为0时,即变为仅考虑木材收益的林地期望价。
3 结果与分析 3.1 ARIMA预测模型的建立对4类立地的蓄积量和碳储量共8组时间序列数据进行检验,发现原始数据不满足建立ARIMA模型的前提,即数据要求正态性、零均性、平稳性。经过零均化和一阶差分后,所有数据都通过Daniel检验和卡方值检验(P > 0.05),表明数据已平稳且呈正态分布。对生成的新序列进行样本自相关函数和偏相关函数的截尾性、拖尾性分析,确定模型的类型和阶次,再依据模型的估计参数对结果进行检验,筛选得到最佳的时间序列模型。运用DPS 7.05建立时间序列预测模型(表 1),表明杉木人工林蓄积量和碳储量均可以使用ARIMA(2,1,3)或ARIMA(3,1,2)模型组合形式表征。结果中Ⅱ类立地碳储量ARIMA(3,1,2)预测模型的R2最低(88.460%),其余预测模型的R2都大于90%,且所有模型的残差序列都为白噪声。模型验证指标表明所建立的蓄积量和碳储量ARIMA预测模型是有效的。限于篇幅,本文仅列举了Ⅰ类立地(12~14 m)的预测结果精度分析,见表 2。由于建模前进行了一阶差分的数据转换,故模型的预测结果从9年开始。从表 2来看,无论是蓄积量还是碳储量,预测结果的绝对误差都较小。从相对误差来看,蓄积量预测中相对误差的最大值为0.95%(16年),平均值为0.27%;碳储量预测中相对误差的最大值为0.84%(15年),平均值为0.28%。说明运用时间序列预测模型对林分现实数据的拟合具有很高的精度,可以为林分经济收益分析提供较为准确的林分生长基础数据。
|
|
|
|
根据收集的经济指标,以ARIMA模型预测的蓄积量和碳储量结果为基础数据,按式(10)和(11)分别计算单一木材经济收益和碳汇木材复合经济收益2种情况下不同立地类型的杉木人工林经济收益。其中利率取5%,碳价格取按式(6)计算得到的2012年理论碳价格173元·t-1。限于篇幅,本文仍仅列出Ⅰ类立地的各年份经济收益计算结果,见表 3。由表 3可知,对立地指数为12~14 m的林分,仅考虑木材经济收益时,ANPV得到最优轮伐期18年,最大值年均净现值1 137.58元·hm-2;LEV的结果为最优轮伐期19年,最大林地期望值32 296.44元·hm-2。在碳汇木材复合经营目标下,2种方法计算得到的最优轮伐期仍然是18年和19年,但由于考虑了碳汇收益,与单一木材经济收益相比,林分最大经济收益分别增加了10.12%(ANPV)和10.72%(LEV)。从各年计算结果来看,林分经济收益都是先随林龄增加而不断上升,达到极大值后开始逐年降低。这主要是由于林分蓄积量和碳储量随林龄增加而不断增大,达到某一林龄阶段后增加速度逐渐趋于平缓。此外,规格材出材率的比例也随林龄增加而增大,而非规格材比例逐渐降低,达到某一林龄阶段后二者比例趋于稳定。因此,随着时间的推移,森林经营效益不断上升,在某一林龄达到极大值,这时所对应的林龄即认为是以经济成熟为目标的最优轮伐期。类似地,计算Ⅱ,Ⅲ,Ⅳ类立地基于2类经营目标的最优轮伐期及经济收益,结果见表 4。对于本案例的杉木人工林,在考虑碳汇收益后,各类立地林分的最佳轮伐期均未产生变化,表明在当前经营成本、木材和碳价格以及利率水平下,经营者不用改变原定的采伐策略也能获得最大复合经济收益。
|
|
|
|
在现实营林过程中,影响最优轮伐期的因素较多。碳汇木材复合经济收益主要由木材收益和碳汇收益2部分组成,根据式(10)和(11),影响碳汇收益的主要因素有碳储量(立地质量)、碳价格和利率。本文就这3个因素对最优轮伐期的影响进行敏感性分析。
3.3.1 立地质量立地质量是影响林分生长发育的决定性因素,与蓄积量和碳储量之间有着十分密切的关系。通常采用地位指数来衡量立地质量的高低(郭艳荣等,2012)。由表 4可知,在复合经营目标下,随着地位指数的升高,最优轮伐期呈现出提前的趋势,相对应的最大年均净现值和林地期望值也呈单调递增,其变化范围为1 252.69~4 368.52元·hm-2 (ANPV)和35 760.09~121 842.58元·hm-2(LEV);与之相反,复合经营的最大收益相比单一经营时的增加幅度却随着立地质量的提高而降低,2种方法的计算结果分别为10.12%~6.55%(ANPV)和10.72%~6.60%(LEV)。这说明在复合经营目标下,碳汇收益对低立地质量杉木林分的总收益提升作用更明显,有利于低质量林业用地的维持,促进对杉木的投资经营。
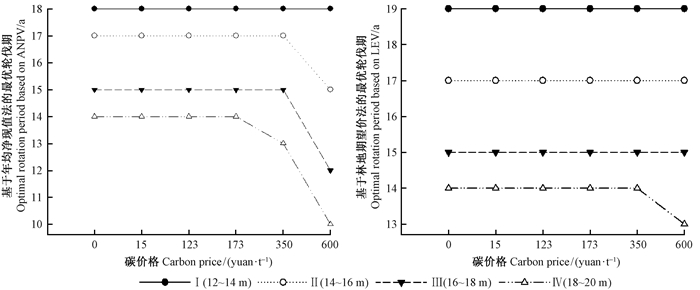
3.3.2 碳价格为了探讨碳价格变化对最优轮伐期及复合经济收益的影响,将碳价格设定在0~600元·t-1的变动区间,利率仍取5%,选取了一系列有代表性的价格进行计算:碳价格为0元·t-1时意味着仅考虑木材收益;15元·t-1和123元·t-1代表我国碳交易所至今为止已成交碳交易中最小和最大成交价;173元·t-1是根据Uzawa碳税率公式推导的理论碳价格;350元·t-1约是理论碳价格的2倍;600元·t-1在本例中可以认为是木材价格的一半。结果发现,不同立地条件下,随着碳价格的增加,最优轮伐期呈现出提前的规律(图 1)。从图 1中还可以看到,碳价格在较长的变动范围内并未对杉木人工林最优轮伐期产生明显影响,以ANPV计算,当碳价格提升到350元·t-1时,Ⅳ类立地的最优轮伐期开始提前,当碳价格达到600元·t-1时,除Ⅰ类立地外,其余3类立地的最优轮伐期都不同程度地提前;而以LEV计算,仅Ⅳ类立地在碳价格为600元·t-1时其最优轮伐期提前到13年,其余立地类型的林分最优轮伐期皆不变。究其原因,是因为碳汇收益相较木材收益占总林地期望值的比重小,最大林地期望值对碳价格变化的响应敏感性较低,只有当碳价格提高到一定程度,如木材价格一半时,LEV法下的最优轮伐期才会有所变化。从复合收益的最大年均净现值和林地期望值(图 2)来看,随着碳价格提高,杉木人工林经济收益不断增加。当碳价格由0提升至600元·t-1后,不同立地质量的林分收益增加25.01%~35.09%(ANPV)和22.90%~37.19%(LEV)。由此可见,由于木材收益占总收益的比重大,在目前木材市场价格远高于碳价格的情况下,杉木最佳轮伐期对碳价格变动的响应并不敏感,只有当碳汇收益提高到足以弥补提前采伐带来的木材收益损失时,最优轮伐期才会开始提前。此外,虽然碳价格变化引起最佳轮伐期发生变化后会导致森林木材收益也随之变化,但在复合经营目标下杉木经营者能多获得额外的碳汇收益。总体上来看,随着碳价格的提高,总经济收益都能大幅度增加,投资效益明显提升。
|
图 1 不同碳价格水平对碳汇木材复合经营下杉木人工林最优轮伐期的影响 Fig.1 Optimal rotation periods in consideration of carbon sequestration and timber economic benefits based on different carbon prices for a Chinese fir plantation |

|
图 2 不同碳价格水平对杉木人工林碳汇木材复合经济收益最大值的影响 Fig.2 The maximum economic benefits of carbon sequestration and timber based on different carbon prices for a Chinese fir plantation |
森林经营作为一种特殊的长期投资行为,利率水平对经济收益具有直接影响,将碳汇收益纳入营林目标后,探讨利率对不同立地条件的最优轮伐期及经济收益的影响显得尤为重要。鉴于Uzawa推导的碳税率价格公式中涉及利率这一变量,故本文采用123元·t-1,即我国碳交易中实际最大成交价作为碳价格,计算不同利率水平下杉木最优轮伐期和复合经济收益(表 5)。从表 5可以发现,利率的变化对最优轮伐期具有显著影响,随着利率提高,最优轮伐期不断提前,利率越大,复合经营目标下杉木人工林最优轮伐期越短。在利率较低时,每提高1%,其最优轮伐期变动幅度较大,如利率从3%增加到4%,Ⅳ类立地最优轮伐期提前了4年(APNV)和3年(LEV)。但从表 5中也可以发现,虽然ANPV和LEV 2种计算方法下最优轮伐期随着利率提升而提前的趋势大致相同,但变化幅度却存在很大差异,比如对Ⅱ类立地来说,当利率为4%时,ANPV和LEV得到的最优轮伐期都是17年,当利率提高到7%时,ANPV得到的最优轮伐期变成10年,而LEV得到的结果仍然是17年。探索其原因,是因为在现有的经营水平下,利率上升后森林经营的机会成本将上升,从而导致投资营林的积极性随之降低,由于ANPV是计算年均收益,对利率的变化更为敏感,而LEV是计算总林地价值,即使利率提高会导致总林地价值降低,但如果无法弥补提前采伐所造成的损失,杉木经营者仍然会选择继续原先的经营方案,因而表 5中用ANPV计算的最优轮伐期变化较大。类似地,虽然不同立地条件下最大年均净现值和林地期望值均随着利率的提高呈现出降低趋势,但变化幅度也存在差异。以Ⅱ类立地为例,在4%和7% 2种利率下,以LEV计算结果来看,虽然最优轮伐期都同样为17年,但在4%利率时最大林地期望值几乎是7%利率时的3倍。因此利率变动会对林分经济收益产生巨大影响,利率的提高对复合目标下杉木人工林的经营是不利的。
|
|
发展森林碳汇经济已经成为应对全球气候变化的重要趋势。森林碳汇具有潜在的生态经济价值,使森林经营者在获得木材收益的同时,还能得到相应的碳汇收益,所以在碳汇木材复合经营目标下,对森林经济收益进行评估是十分有必要的。经济收益评估以林分蓄积量的估算为基础,而林分蓄积量受诸多因素的影响,如单株材积、林分密度、立地质量等,所以林分蓄积量的准确预测是经济收益分析结果可靠性的保证。然而许多学者在分析碳交易背景下的林分经济收益时,所采用的产量预估模型都存在局限性,多使用前人研究的相关区域的理论生长模型,在进行蓄积量估算时缺乏对模型适用性的分析及必要的模型修正,因此即使研究区域相似、研究对象相同,其研究结果也存在较大差异。如沈月琴(2013b)和朱臻(2013b)同样是基于浙江和江西省杉木调查数据,都使用陈则生(2010)提出的杉木生长模型预测林分生长数据,但前者发现当碳价格达到200元·t-1时,在复合经营目标下优等地杉木林分的最优轮伐期开始变化,而后者的结论却是只有当碳价格上升到800元·t-1时,优等地杉木林分的最优轮伐期才开始变化。鉴于此,为了获得更加准确的林分产量预测,本研究利用现实杉木林分调查数据,在林分尺度上建立时间序列预测模型(ARIMA)对蓄积量和碳储量进行拟合预测,再以此为基础分析实地案例中杉木林分经济收益和最优轮伐期的变化。时间序列预测是按一定时序的规律进行的,其前提是调查对象在一定时期内不受较大的外生因素的影响,即应该具有内生稳定性,故本研究在获取数据时有针对性地选择初植密度相近且间伐总强度较低的林分,按照立地质量进行分类,以空间代时间的方法完成对林分蓄积量和碳储量时间序列数据的预处理。从结果上来看,ARIMA模型的预测准确度较高,因此认为利用时间序列模型对现实林分生长进行预测是值得尝试和推广的。
基于时间序列预测的结果,将碳汇收益纳入到杉木人工林经济收益的计算模型中,利用年均净现值法和林地期望价法探讨了碳汇木材复合经济经营对杉木人工林经济成熟的影响,同时比较分析了林分最优轮伐期和最大经济收益对立地质量、碳价格、利率这3个不确定因素变化的响应。在本研究的实地案例中主要结果有:
1) 在目前木材价格远远高于碳价格的情况下,增加碳汇目标不会改变原来的采伐策略,但复合经济收益的增加是十分明显的。这说明在现有的杉木经营状况下,木材收益和碳汇收益2个不同的经营目标可以兼容,经营者不用改变轮伐期就能获取最大复合收益,有利于经营者增加收入,增强其从事杉木经营的积极性。
2) 立地质量越好,杉木生长速度越快,更有利于单株材积和林分蓄积量的积累,故复合经营目标下最优轮伐期随着地位指数上升而提前,最大复合经济收益也随之明显提高。因此,尽量选择立地条件较好林地进行杉木造林,能提高经营者的经济收入。
3) 碳价格在较长变化范围内对最优轮伐期的影响并不显著,只有当碳价格提高一定程度时,最优轮伐期才有提前的趋势,且随着碳价格的提高,复合经济收益明显增加。由于在现有经营水平下,不用提前或推迟采伐时间就能获得额外的碳汇收益,因为碳价格提高能有效提升杉木经营者的投资效益。
4) 随着利率的增加,碳汇木材复合经营目标下杉木人工林最优轮伐期不断提前,但最大复合经济收益明显降低,因此高利率不利于杉木人工林的经营。
本研究也存在一些不足之处。ARIMA时间序列预测模型虽然在本案例中预测结果较好,但是该模型存在随着预测时期延长预测误差逐渐增大的缺陷,所以在实践中必须对模型不断加以调整,以确保得到最佳的预测效果。此外,本文仅探讨了碳价格和利率2个经济因素对碳汇价值的影响,而实际影响最优轮伐期和碳汇收益的经济因素还包括政府政策补贴、碳汇监测和交易成本等,这些值得后续深入分析与研究。
| [] |
陈则生. 2010. 杉木人工林经济成熟龄的研究. 林业经济问题 , 30 (1) : 22–26.
( Chen Z S.2010. The research on age at economic maturity of Chinese fir plantations. Issues of Forestry Economics , 30 (1) : 22–26. [in Chinese] ) |
| [] |
陈冲影. 2010. 森林碳汇与农户生计--以全球第一个森林碳汇项目为例. 世界林业研究 , 23 (5) : 15–19.
( Chen C Y.2010. Forestry carbon sequestration and local households' livelihoods:taking the first CDM forestry carbon project in the world as example. World Forestry Research , 23 (5) : 15–19. [in Chinese] ) |
| [] |
郭艳荣, 吴保国, 刘洋, 等. 2012. 立地质量评价研究进展. 世界林业研究 , 25 (5) : 47–52.
( Guo Y R, Wu B G, Liu Y, et al.2012. Research progress of site quality evaluation. World Forestry Research , 25 (5) : 47–52. [in Chinese] ) |
| [] |
简盖元, 冯亮明, 刘伟平. 2011. 基于碳汇价值的森林最优轮伐期分析. 林业经济问题 , 31 (1) : 70–75.
( Jian G Y, Feng L M, Liu W P.2011. Analysis of forest optimal rotation which base on the value of carbon sequestration. Issues of Forestry Economics , 31 (1) : 70–75. [in Chinese] ) |
| [] |
李怒云, 宋维明. 2006. 气候变化与中国林业碳汇政策研究综述. 林业经济 (5) : 60–64, 80.
( Li N Y, Song W M.2006. Summary for climate change and forestry carbon sequestration policy under CDM in China. Forestry Economics (5) : 60–64, 80. [in Chinese] ) |
| [] |
彭志行, 鲍昌俊, 赵杨, 等. 2008. ARIMA乘积季节模型及其在传染病发病预测中的应用. 数理统计与管理 , 27 (2) : 362–368.
( Peng Z H, Bao C J, Zhao Y, et al.2008. ARIMA product season model and its application on forecasting in incidence of infectious disease research. Application of Statistics and Management , 27 (2) : 362–368. [in Chinese] ) |
| [] |
权伟, 应苗苗, 康华靖, 等. 2014. 基于时间序列模型的洞头大型藻类碳汇强度预测分析. 中国农学通报 , 30 (8) : 63–67.
( Quan W, Ying M M, Kang H J, et al.2014. Carbon sink capacity forecast of macroscopic algae in the coastal areas of Dongtou County based on time series model. Chinese Agricultural Science Bulletin , 30 (8) : 63–67. [in Chinese] ) |
| [] |
任腾腾, 徐秀英. 2013. 碳交易情景下林地效益可能的变化分析--基于农户杉木地块调查分析. 生态经济:学术版 (2) : 158–161, 182.
( Ren T T, Xu X Y.2013. The analysis of forestland benefit possible changes of different types in carbon trading situation:based on Chinese fir plot investigation of farmer. Ecological Economy, (2):158-161 (2) : 158–161, 182. [in Chinese] ) |
| [] |
沈月琴, 王枫, 张耀启, 等. 2013a. 中国南方杉木森林碳汇供给的经济分析. 林业科学 , 49 (9) : 140–147.
( Shen Y Q, Wang F, Zhang Y Q, et al.2013a. Economic analysis of Chinese fir forest carbon sequestration supply in south China. Scientia Silvae Sinicae , 49 (9) : 140–147. [in Chinese] ) |
| [] |
沈月琴, 王小玲, 王枫, 等. 2013b. 农户经营杉木林的碳汇供给及其影响因素. 中国人口·资源与环境 , 23 (8) : 42–47.
( Shen Y Q, Wang X L, Wang F, et al.2013b. Carbon sequestration supply and its influencing factors for farmers operating Fir in Chinese southern collective forest zone. China Population Resources and Environment , 23 (8) : 42–47. [in Chinese] ) |
| [] |
王枫, 沈月琴, 朱臻, 等. 2012. 杉木碳汇的经济学分析:基于浙江省的调查. 浙江农林大学学报 , 29 (5) : 762–767.
( Wang F, Shen Y Q, Zhu Z, et al.2012. Economic analysis of Chinese fir forest carbon sequestration:based on Zhejiang's survey. Journal of Zhejiang A & F University , 29 (5) : 762–767. [in Chinese] ) |
| [] |
王志忠, 刘秀菊, 王树林, 等. 2007. 黄河流域棉花品种产量性状时间序列的ARIMA模型预测研究. 棉花学报 , 19 (3) : 220–226.
( Wang Z Z, Liu X J, Wang S L, et al.2007. Prediction of time series of main yield characters for cotton varieties in the Yellow River valley region using ARIMA models. Cotton Science , 19 (3) : 220–226. [in Chinese] ) |
| [] |
吴承祯, 洪伟. 1995. 福建省杉木人工林序列林价及其应用研究. 福建林学院学报 , 15 (3) : 218–222.
( Wu C Z, Hong W.1995. Study on the forest value list of Chinese fir plantation in Fujian province and its application. Journal of Fujian College of Forestry , 15 (3) : 218–222. [in Chinese] ) |
| [] |
熊志斌. 2011. 基于ARIMA与神经网络集成的GDP时间序列预测研究. 数理统计与管理 , 30 (2) : 306–314.
( Xiong Z B.2011. Researeh on GDP time series forecasting based on integrating ARIMA with neural networks. Journal of Applied Statistics and Management , 30 (2) : 306–314. [in Chinese] ) |
| [] |
续珊珊. 2011. 中国森林碳汇问题研究--以黑龙江省森工国有林区为例. 北京: 经济科学出版社 .
( Xu S S. 2011. Research on forest carbon sequestration in China:a case study of forest industrial state-owned region in Heilongjiang Province. Beijing: Economic Science Press . [in Chinese] ) |
| [] |
于金娜, 姚顺波. 2012. 基于碳汇效益视角的最优退耕还林补贴标准研究. 中国人口·资源与环境 , 22 (7) : 34–39.
( Yu J N, Yao S B.2012. Optimal subsidy of SLCP in China from the perspective of carbon sequestration benefit. China Population Resources and Environment , 22 (7) : 34–39. [in Chinese] ) |
| [] |
朱臻, 沈月琴, 张耀启, 等. 2013a. 碳汇经营目标下的林地期望价值变化及碳供给--基于杉木裸地造林假设研究. 林业科学 , 48 (11) : 112–116.
( Zhu Z, Shen Y Q, Zhang Y Q, et al.2013a. Change of forestland expected value and carbon supply in sequestration:based on the Chinese fir plantation the in objective of carbon bared land. Scientia Silvae Sinicae , 48 (11) : 112–116. [in Chinese] ) |
| [] |
朱臻, 沈月琴, 吴伟光, 等. 2013b. 碳汇目标下农户森林经营最优决策及碳汇供给能力--基于浙江和江西两省调查. 生态学报 , 33 (8) : 2577–2585.
( Zhu Z, Shen Y Q, Wu W G, et al.2013b. Household optimal forest management decision and carbon supply:case from Zhejiang and Jiangxi Provinces. Acta Ecologica Sinica , 33 (8) : 2577–2585. DOI:10.5846/stxb [in Chinese] ) |
| [] | Asante P, Armstrong G W, Adamowicz W L.2011. Carbon sequestration and the optimal forest harvest decision:a dynamic programming approach considering biomass and dead organic matter. Journal of Forest Economics , 17 (1) : 3–17. |
| [] | Box G E P, Jenkins G M, Reinsel G C. 2011. Time series analysis:forecasting and control. John Wiley & Sons . |
| [] | Diaz-Balteiro L, Rodriguez L C E.2006. Optimal rotations on Eucalyptus plantations including carbon sequestration-a comparison of results in Brazil and Spain. Forest Ecology and Management , 229 (1) : 247–258. |
| [] | Dixon R K, Solomon A M, Brown S., et al.1994. Carbon pools and flux of global forest ecosystems. Science , 263 (5144) : 185–190. DOI:10.1126/science.263.5144.185 |
| [] | Fahey T J, Woodbury P B, Battles J J, et al.2009. Forest carbon storage:ecology, management, and policy. Frontiers in Ecology and the Environment , 8 (5) : 245–252. |
| [] | Fang J, Chen A, Peng C, et al.2001. Changes in forest biomass carbon storage in China between 1949 and 1998. Science , 292 (5525) : 2320–2322. DOI:10.1126/science.1058629 |
| [] | Guthrie G, Kumareswaran D.2009. Carbon subsidies, taxes and optimal forest management. Environmental and Resource Economics , 43 (2) : 275–293. DOI:10.1007/s10640-008-9238-4 |
| [] | Hartman R.1976. The harvesting decision when a standing forest has value. Economic Inquiry , 14 (1) : 52–58. DOI:10.1111/ecin.1976.14.issue-1 |
| [] | Pan Y, Birdsey R A, Fang J, et al.2011. A large and persistent carbon sink in the world's forests. Science , 333 (6045) : 988–993. DOI:10.1126/science.1201609 |
| [] | Richards K R, Stokes C.2004. A review of forest carbon sequestration cost studies:a dozen years of research. Climatic Change , 63 (1/2) : 1–48. DOI:10.1023/B:CLIM.0000018503.10080.89 |
| [] | Stainback G A, Alavalapati J R R.2002. Economic analysis of slash pine forest carbon sequestration in the southern US. Journal of Forest Economics , 8 (2) : 105–117. DOI:10.1078/1104-6899-00006 |
| [] | Uzawa H. 1991. Global warming initiatives:the Pacific Rim//Dornbusch R, Poterba J M. Global Warming:Economic Policy Responses, 275-324. |
 2016, Vol. 52
2016, Vol. 52

