文章信息
- 王正, 顾玲玲, 高子震, 刘斌
- Wang Zheng, Gu Lingling, Gao Zizhen, Liu Bin
- SPF规格材弹性模量的动态测试及其概率分布
- Dynamic Testing and Probability Distribution of Elastic Modulus of SPF Dimension Lumbers
- 林业科学, 2015, 51(2): 105-111
- Scientia Silvae Sinicae, 2015, 51(2): 105-111.
- DOI: 10.11707/j.1001-7488.20150213
-
文章历史
- 收稿日期:2014-04-11
- 修回日期:2014-09-13
-
作者相关文章
2. 南京林业大学机械电子工程学院 南京 210037
2. College of Mechanical and Electronic Engineering, Nanjing Forestry University Nanjing 210037
SPF规格材是轻型木结构建筑中的主材,其弹性模量是衡量材料产生弹性变形难易程度的指标(郑栋梁等,2002),因此SPF规格材弹性模量测定及分析尤为重要(Linda et al., 1997;Zhu et al., 2010)。为提高对弹性模量的检测水平以及对弹性模量数据的统计分析范围,笔者从南京北美木屋有限公司一批SPF规格材中随机抽取容量为300的样本作为试件,采用弹性绳垂直自由悬挂方式的支承结构对试件实现自由梁,模态试验验证了自由梁的精度。在瞬态激励下,通过测试试件一阶弯曲频率,得到其弹性模量(王正,2007); 应用应力波法验证了频率法测试结果的正确性(Raini et al., 2000)。 测试数据的精确性是数据处理正确性的前提。一般地,数据统计分析应用最多的是正态分布,本文除应用频率法精确地测量弹性模量外,还探讨应用威布尔分布来分析SPF规格材弹性模量数据的可行性。根据实测的子样弹性模量数据,对其进行直线拟合和K-S法检验,结果表明SPF规格材弹性模量除服从三参数威布尔分布外,还服从正态分布。最后,根据加拿大SPF规格材二级材弹性模量在8 000~9 000 MPa标准,借助威布尔分布和正态分布分别推算了总体二级规格材达标的概率。
1 瞬态激励频率法测量SPF规格材弹性模量 1.1 测试原理根据梁横向弯曲理论,自由梁的一阶弯曲频率与弹性模量E的关系(提摩盛科,1965)为:
| $E = 0.946\frac{{\rho f_1^2{L^4}}}{{{h^2}}}$ | (1) |
通过测试自由梁的一阶弯曲频率f1,由式(1)推算出弹性模量。
1.2 试件和测试方法本试验所用的加拿大SPF规格材成品试件共300块,其材面标识级别为Ⅱ级,规格尺寸为3 670 mm(l)×138 mm(b)×37 mm(h)。依据GB/T 1933—2009《木材密度测定方法》,逐一测试计算试件的气干密度ρ=390~492 kg·m-3、含水率为11%~13%。
采用瞬态激励振动法(Wang et al., 2012;Ilic,2003),用橡皮锤敲击SPF规格材试件使其产生横向自由振动,测试试件频谱,从频谱图中识别出试件一阶弯曲频率f1。SPF规格材试件和测试系统框图见图 1。
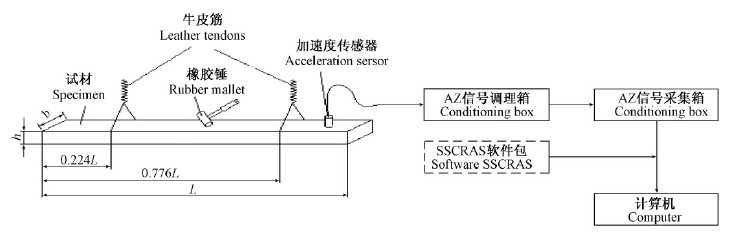 |
图 1 SPF试件的基频测试系统 Fig. 1 Testing system flow chart of natural frequency of SPF testing lumbers |
对26号试件进行模态试验结果得知,前四阶频率中第二阶、第三阶和第四阶频率与第一阶频率比以及前四阶振型节点位置与其理论解析解完全一致,这说明文中试验的悬挂实现了自由支承,由此提出用瞬态激振法测试试件一阶弯曲频率的试验方案(Wang et al., 2012;张令弥,1992;傅志方,2002)。
1)采集参数设置: 分析频率设为50 Hz,FFT长度为2 048(频率测试精度可达0.062 5 Hz),采集方式为自由运行,数据块1块,电压范围 ±1 250 mV(程控放大4倍),调理仪放大倍率设为100。滤波频率设为50 Hz,防止频率混迭,以保证在频谱上不会出现三阶固有频率的混迭频率(假频率)。
2)加速度计安装于试件左端或右端,橡胶锤敲击试件跨中。跨中是二阶弯曲振型节点位置,使得在50 Hz分析频率的频谱图上不出现二阶频率的峰值。
图 2为SPF规格材26号试件的频谱,从频谱图上可读出一阶弯曲频率,即基频为13.88 Hz。从图 2还看到在2 Hz附近出现了2个小高峰,分别对应的是试件刚体平动和转动模态。
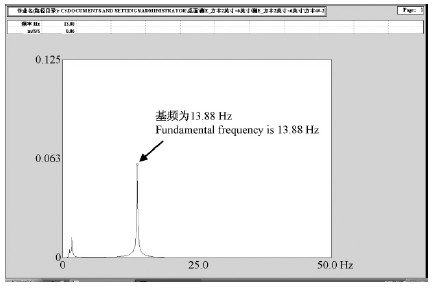 |
图 2 SPF规格材的26号试件测量频谱 Fig. 2 Measured spectrum of No.26 piece of SPF dimension lumbers |
本文根据梁横向弯曲振动理论测得300块SPF规格材成品件试件的弹性模量。为说明测试的正确性,可用其他方法加以验证,例如静态法或依据于杆件纵向振动理论的应力波法(Wang et al., 2007)。考虑到试件长度为3 670 mm,不宜在拉伸机上静态测量材料的弹性模量,故本文釆用应力波法和频率法对1~50号试件进行一一检测。检测仪器为新西兰产HM200原木品质测量仪。每根试件重复测量3次,取其平均值作为波速v,弹性模量E的计算公式为E=ρv2,应力波法和频率法测弹性模量的散点图和相关关系曲线如图 3所示。
 |
图 3 频率法-应力波法测量弹性模量的相关关系 Fig. 3 Correlativity of measuring MOE value by the frequency method and stress wave method |
从图 3看到频率法和波速法测试的弹性模量具有较好的相关性。
3 SPF规格材弹性模量概率分布 3.1 Weibull分布及其数字特征(Weibull et al., 1951)设SPF规格材弹性模量为随机变量ζ,且符合如下的三参数威布尔分布函数F(E):
| $\begin{gathered} \Pr {\text{o}}\left({\zeta \leqslant E} \right)= F\left(E \right)= 1 - \exp \left[ { - {{\left({\frac{{E - {E_{\text{u}}}}}{{{E_0}}}} \right)}^m}} \right],\hfill \\ E{\text{ > }}{E_{\text{u}}}; \hfill \\ \Pr {\text{o}}\left({\zeta \leqslant E} \right)= F\left(E \right)= 0,E{\text{ < }}{E_{\text{u}}} \hfill \\ \end{gathered}$ | (2) |
根据总体平均值μ和标准离差σ定义,借助伽马函数Γ(x),不难导出:
| $\mu = {E_0}\Gamma \left({1 + \frac{1}{m}} \right)+ {E_{\text{u}}}$ | (3) |
| $\sigma = {E_0}\sqrt {\Gamma \left({1 + \frac{2}{m}} \right)- {\Gamma ^2}\left({1 + \frac{1}{m}} \right)} $ | (4) |
将子样的弹性模量测量值按由小到大排列,形成次序统计量Ei(i=1,2,3…,299,300),相应的概率值为i/(n+1)(Gumbel,1958)[若次序统计量Ei有相同值,其重复次数为k,则相应概率值为(i+k)/(n+1)],n为样本容量,现n=300。对于给定的Ei值,则由式(2)有:
| $P\left({\zeta \leqslant {E_i}} \right)= 1 - \exp \left[ { - {{\left({\frac{{{E_{\text{i}}} - {E_{\text{u}}}}}{{{E_0}}}} \right)}^m}} \right]$ |
将次序统计量Ei和相应概率值i/(n+1)代入上式,经对数运算得:
| $\lg \left({\lg \frac{{n + 1}}{{n + 1 - i}}} \right)= m\lg \left({{E_i} - {E_u}} \right)+ \lg \left({\frac{{\lg e}}{{E_0^m}}} \right)$ | (5) |
首先根据实测弹性模量最小值5 526 MPa,设Eu分别取0,2 000,2 500,3 500,4 000,4 500和5 000 MPa。在威布尔坐标系lg(Ei-Eu)-$\left({\lg \frac{{n + 1}}{{n + 1 - i}}} \right)$中,计算$\left[ {\lg \left({{E_i} - {E_u}} \right),\lg \left({\lg \frac{{n + 1}}{{n + 1 - i}}} \right)} \right]$点对的值,若试验数据点对落在一条直线上,则认为弹性模量数据可能符合Weibull分布,且由直线斜率确定m,直线与纵轴的截距确定E0。
当Eu=4 500 MPa时,试验点对在威布尔坐标系中的散点图如图 4所示。
 |
图 4 SPF规格材弹性模量威布尔分布的拟合检验 Fig. 4 Fitting inspection schedule of Weibull distribution with MOE values of SPF dimension lumbers |
当Eu=4 500 MPa时,测量点用直线拟合的相关系数r=0.996 83,n=300,拟合效果好,故SPF规格材弹性模量在威布尔坐标系中可以用一条直线拟合。
由直线斜率及与纵轴截距得m=3.409 6,E0=6 118 MPa。
因此,SPF规格材弹性模量的分布函数可写为:
| $F\left(E \right)= P\left({\zeta \leqslant E} \right)= 1 - \exp \left[ { - {{\left({\frac{{E - 4500}}{{6118}}} \right)}^{3.4096}}} \right]$ | (6) |
概率密度函数为:
| $\begin{gathered} f\left(E \right)= 5.5731 \times {10^{ - 4}}{\left({\frac{{E - 4500}}{{6118}}} \right)^{2.4096}} \hfill \\ \exp \left[ { - {{\left({\frac{{E - 4500}}{{6118}}} \right)}^{3.4096}}} \right] \hfill \\ \end{gathered} $ | (7) |
将m=3.409 6,E0=6 118 MPa,Eu=4 500 MPa代入式(3)和式(4),得总体平均值μ和标准离差σ的估计值为 μ=9 997 MPa,σ=1 781 MPa;变异系数为17.8%。容量为300样本,样本平均值为10 001 MPa,标准离差为1 822 MPa。
对于设定的一系列Eu值,通过直线拟合得到的可能威布尔参数及其推算的SPF规格材总体弹性模量均值和标准离差如表 1所示。
|
|
从表 1可知,对于SPF规格材有一系列可能的威布尔参数(相关系数值不足于说明它们就是威布尔分布参数,详见3.3),推算出基本上相同的总体均值和标准离差。
3.3 威布尔分布和正态分布的K-S检验随机变量分布类型检验一般有2种情况:其一,已知参数估计分布类型;其二,未知参数,先估算参数,后检验分布类型。检验方法有多种,其中K-S 法是最常用的方法,其特点是利用了数据的全部信息。
检验假设H0:SPF规格材总体弹性模量服从威布尔分布,H1:SPF规格材总体弹性模量不服从威布尔分布。
目前,检验假设H0的K-S检验属于参数未知情况,首先要估算参数。表 2已给出一系列可能的威布尔参数估算值,其中的一种可能参数给出一个假设的已知分布函数。然后,计算假设的已知分布函数与经验分布函数在顺序统计量上的差值,对其取绝对值后的最大值就是K-S法中的检验统计量Dn值,计算Dn值全过程可借助Excel完成。最后,根据显著性水平α和样本容量查参数未知时的威布尔分布K-S检验临界值表获得检验统计量的临界值Dn,α,若Dn < Dn,α,接受H0,否则拒绝H0。
|
|
对于一系列可能的威布尔参数所构成的假设的已知分布函数,K-S检验的结果如表 2所示。
以样本均值和标准离差作为正态分布总体均值和标准离差估计值,对这样假设的已知分布函数进行K-S检验,计算Dn步骤同上,不同的是查正态分布参数未知时的Dn,α值,正态分布的检验结果也一并列于表 2。
Dn的临界值Dn,α由样本容量和显著性水平α查表获得(吴世伟等,1990)。
对于威布尔分布:
α=0.05,n=300,在参数未知时,Dn,α=D300,0.05=0.888/$\sqrt {300} $=0.051 27。
对于正态分布:
α=0.05,n=300,在参数未知时,Dn,α=D300,0.05=0.886/$\sqrt {300} $=0.051 15。
从表 2可知:1)SPF规格材弹性模量不服从两参数威布尔分布(Eu=0);2)SPF规格材弹性模量服从于位置参数Eu大于最小测试值一半的三参数威布尔分布;3)SPF规格材弹性模量服从正态分布。
3.4 SPF规格材总体弹性模量在给定值下的概率计算应用被K-S检验接受的三参数威布尔分布和正态分布进行弹性模量在给定值下的概率计算(李云雁等,2004),结果如表 3所示。
|
|
从表 3数据分析可得:
1)以3 500,4 000,4 500 MPa为Eu的设定值时,计算的概率值稳定且基本相同,这时Eu设定值分别是弹性模量测试的最小值5 526 MPa的63%,72%和81%。因此,运用威布尔分布进行SPF规格材弹量模量概率计算时,推荐采用根据实测数据最小值的60%~80%作为位置参数Eu设定值的三参数威布尔分布。
2)三参数威布尔分布和正态分布计算的SPF规格材弹性模量在给定值下的概率相等(精确到小数点后的第3位)。
SPF规格材弹性模量的概率分布曲线和概率密度曲线,可清晰地说明三参数威布尔分布和正态分布计算的概率特点(图 5)。从图 5可以看到:1)威布尔概率密度相对于它的均值(9 997 MPa)略显不对称性,不同于正态概率密度曲线相对于均值是对称的;2)弹性模量不超过7 000 MPa时,正态概率分布曲线略高于威布尔概率分布曲线,超过7 000 MPa后,则正好相反。
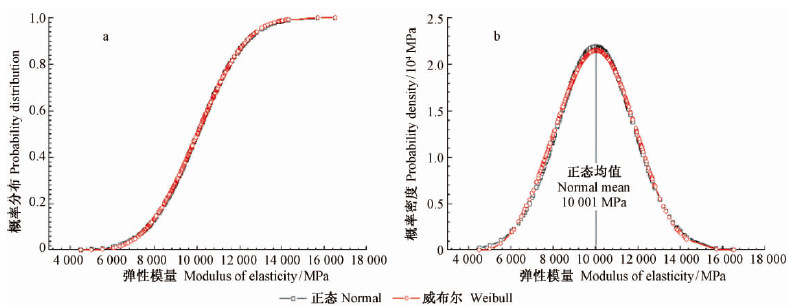 |
图 5 SPF规格材弹性模量的概率分布曲线(a)和概率密度曲线(b) Fig. 5 Probability distribution curve(a) and probability density curve(b) of MOE value of SPF dimension lumbers |
仅从弹性模量这一参数对SPF规格材质量进行评价。成品试件上标识的是加拿大二级规格材,其弹性模量在8 000~9 000 MPa(GB 50005—2003)。由于弹性模量是刚性指标,反映构件抵抗变形能力,变形大小与弹性模量呈反比,故在评价二级材时,只考虑8 000~9 000 MPa范围的下限值8 000 MPa,将8 000 MPa作为给定值计算概率即可。Eu=4 500 MPa三参数威布尔分布推算的SPF规格材弹性模量不超过8 000 MPa的概率为13.8%,而借助于正态分布计算的概率为13.6%。
4 结论1)模态试验验证了文中的试验装置实现了试件自由悬挂的支承条件,提出了频率法的测试方案,保证了一阶弯曲振动固有频率测试精度,可靠地推算出SPF规格材的弹性模量。
2)瞬态激励频率法测试SPF规格材的弹性模量具有简便、快速、重复性好和精度高等优点。
3)频率法和波速法测出的弹性模量具有较好的相关性,验证了频率法测试弹性模量的正确性。
4)SPF规格材总体弹性模量不服从两参数威布尔分布。
5)SPF规格材总体弹性模量服从三参数威布尔分布,在确定威布尔分布参数时,推荐按最小试验数据的60%~80%设定位置参数Eu值。
6)SPF规格材总体弹性模量的三参数威布尔概率密度曲线相对于均值略显非对称性。
7)SPF规格材总体弹性模量除服从三参数威布尔分布外,还服从正态分布。正态分布计算的弹性模量不超过
7 000 MPa的概率高于威布尔分布的计算值,在其他范围,2种分布计算的概率值是相同的。
8)应用三参数威布尔分布和正态分布推断SPF规格材总体的弹性模量达不到加拿大二级规格材所规定的下限标准值,即8 000 MPa的概率分别为13.8%和13.6%。
| [1] |
傅志方. 2002.振动模态分析与参数辨识. 北京: 机械工业出版社, 2-56. (Fu Z F. 2002. Modal analysis of vibration and parameter identification. Beijing:China Machine Press, 2-56.[in Chinese])(  1) 1)
|
| [2] |
李云雁, 胡传荣. 2004.设计与数据处理. 北京: 化学工业出版社. (Li Y Y, Hu C R. 2004. Design and data processing. Beijing: Chemical Industry Press.[in Chinese])(  1) 1)
|
| [3] |
提摩盛科. 1965.机械振动学.北京: 机械工业出版社, 316-333. (Timoshenko S. 1965. Mechanical vibrational science. Beijing:China Machine Press, 316-333.[in Chinese])(  1) 1)
|
| [4] |
王正. 2007.两种木质复合材料弹性模量与阻尼比的动态测量.南京林业大学学报, 31(3): 147-149. (Wang Z. 2007. Dynamic measure of elasticity model and damp ratio to HDF and OSB. Journal of Nanjing Forestry University, 31(3):147-149.[in Chinese])(  1) 1)
|
| [5] |
吴世伟, 叶 军. 1990.参数未知的K-S法检验临界值分析.港工技术, (1): 16-20(Wu S W, Ye J. 1990. The unknown parameters of the K-S method to test the critical value analysis. Port Engineering Technology, (1): 16-20.[in Chinese])(  1) 1)
|
| [6] |
张令弥. 1992.振动测试与动力分析. 北京: 航空工业出版社, 123-230. (Zhang L M. 1992. Vibration measurement and dynamic analysis. Beijing:Aircraft Industry Press, 123-230.[in Chinese])(  1) 1)
|
| [7] |
郑栋梁, 李中付, 华宏星. 2002. 结构早期损伤识别技术的现状和发展趋势. 振动与冲击, (2): 1-6. (Zheng D L, Li Z F, Hua H X. 2002. Current situation and development trend of early structural damage identification technology.Vibration and Shock, (2):1-6[in Chinese]).(  1) 1)
|
| [8] |
Gumbel E J. 1958.Statistics of Extremes. New York: Calumbia University Press.( 1) 1)
|
| [9] |
Ilic J. 2003.Dynamic MOE of 55 species using small wood beams. Holz Roh Werkst, 61(3): 167-172.( 1) 1)
|
| [10] |
Linda S B, Donald A D, et al. 1997. Mechanically graded lumber: the grading agency perspective. Wood Design Focus, Summer, 3- 6( 1) 1)
|
| [11] |
Raini C R, Francis G W, Tnomas M G, et al. 2000.Sress-wave analysis of douglas-fir logs for veneer properties. Forest Products Journal, 50(4): 49-52( 1) 1)
|
| [12] |
Wang X P, Carter P, Ross R J, et al. 2007.Acoustic assessment of wood quality of raw forest materials—a path to increase profitability. Forest Products Journal, 57(5): 6-14. ( 1) 1)
|
| [13] |
Weibull W, Swenden S. 1951.A statistical distribution of function wide applicability. J of Applied Mechanics, 18: 293-297.( 1) 1)
|
| [14] |
Wang Z, Li L, Gong M. 2012.Dynamic modulus of elasticity and damping ratio of wood-based composites using a cantileverbeam vibration technique. Construction & Building Materials, 28(1): 831-834.( 2) 2)
|
| [15] |
Zhu X D, Wang F H, Cao J, et al. 2010.Nondestructive test system for wood vibration based on virtual instrument. Journal of Northwest Forestry University, 25(5): 182-186.( 1) 1)
|
 2015, Vol. 51
2015, Vol. 51
