文章信息
- 齐英杰, 孙奇, 马岩
- Qi Yingjie, Sun Qi, Ma Yan
- 车用木橡胶减震器动态力学性能及Johnson-Cook型本构方程
- Dynamic Mechanical Properties and Johnson-Cook Type Constitutive Equation of Wood Rubber Shock Absorber for Vehicle
- 林业科学, 2015, 51(12): 149-155
- Scientia Silvae Sinicae, 2015, 51(12): 149-155.
- DOI: 10.11707/j.1001-7488.20151218
-
文章历史
- 收稿日期:2015-02-02
- 修回日期:2015-07-17
-
作者相关文章
近年来,随着人们生活水平的提高,促进了汽车消费需求的不断增加,加快了汽车技术的发展速度,使得汽车的各项性能不断提高。汽车是一个由很多元器件组成的整体,其中应用到橡胶减震器的部件可根据其使用部位分为发动机系列用、驱动装置用、操纵装置用、前后悬挂用、车身用、排气系统用和其他系统用七大类,可见橡胶减震器在汽车上的应用之多。然而因此产生大量的废弃橡胶减震器不仅造成了大量资源的浪费,而且对环境也造成了一定的污染。目前,废弃橡胶的回收再利用对世界各国来说仍然是个难题。
木橡胶是近年来提出来的,是基于金属橡胶的理念和形成机制,结合近代木材微米加工理论,以微米木丝为基材,利用冷硫化和复合材组构理论,采用热压模具定型加工出来的一种新型木基高弹性复合材料。其中,微米木丝的制作原料主要来源于林间及木材加工剩余物,其来源广泛、成本低,而且还能提高木材的利用率,属于环保材料(袁旭等,2014; 马岩等,2008; 2014)。木材本身是阻尼材料,经过硫化复合成型后的木橡胶,既具有木质材料的结构和性能,又具有与橡胶材料结构高度相似的优异特征,使其成为一种具有较高潜力的新型减震材料。本文在室温下对木橡胶及氯丁胶模压出的橡胶减震器试样进行动态压缩试验,在分析不同应变率下的应力-应变曲线后,利用试验数据初步建立了木橡胶减震器的Johnson-Cook型本构方程,并检验求得的本构方程对车用木橡胶减震器应力与应变关系的描述是否准确。
1 材料与方法 1.1 木橡胶减震器试样的制备选取密度0.439 g·cm-3、含水率约12%的小兴安岭红松(Pinus koraiensis)木块加工而成的微米木丝及弹性好、黏接强度高、胶层柔韧、耐冲击、耐震动的氯丁胶为试验材料,采用微米长木纤维成型机床加工干燥后的红松木块。为了消除木材细胞原有的微观缺陷,保留木材细胞原有弹性,得到光滑的微米级长丝纤维,加工时需沿纵向(顺纹)进行加工,然后将加工好的木纤维放入揉丝机揉搓至宽度为1~2 mm、长度为15~30 mm的微米木丝(图 1)备用(马岩,2003; 杨春梅等,2014)。
 |
图 1 加工后的微米长细丝形态 Fig. 1 Forming micron long filaments shape |
称量制备木橡胶减震器所需的微米木丝及氯丁胶(氯丁胶的用量为微米木丝质量的40%),按少量、多次的原则进行拌胶,以防止一次性拌胶过多导致微米木丝与胶黏剂接触不充分从而影响木橡胶减震器的力学性能。
拌胶完成后需要利用模压设备完成进料、模压、卸模等过程。本文选用由东北林业大学林业与木工机械工程技术中心研制的木橡胶模压设备模压木橡胶减震器试样,该设备的最大压力可达4~7 MPa,能够满足试验的使用要求。
选定好试验设备后,将机油涂抹在模具上并开始进料。进料过程中要多次进料,每次进料不宜过多;而且为了保证冲压均匀,需进料1次冲压1次,冲压力的大小也要随着进料次数的增加而增加。待进料结束后,将模压的木橡胶减震器试样加热至150~180 ℃,加热8~10 min之后再保压30~60 min,待模具温度降至室温即可开模(马岩等,2014)。模压出的木橡胶减震器试样见图 2。
 |
图 2 木橡胶减震器试样 Fig. 2 Wood rubber shock absorber specimen |
分离式霍普金森压杆是利用试验杆的一维应力波理论以及弹性波透射、反射原理来获得材料应变率为102~104s-1时的应力-应变关系,其装置示意见图 3。
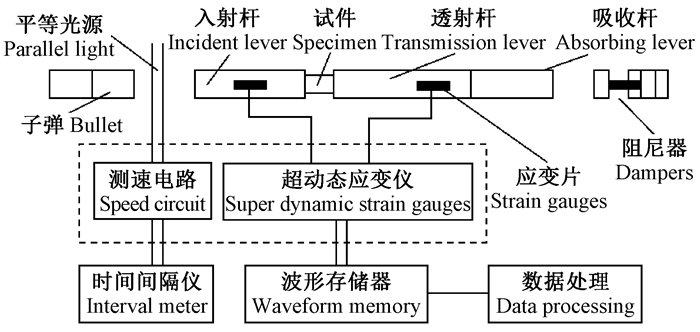 |
图 3 分离式霍普金森压杆装置示意 Fig. 3 Schematic of SHPB |
本文利用分离式霍普金森压杆在室温下对木橡胶减震器试样(φ10 mm×10 mm)进行动态压缩试验,试验应变速率为1 250,1 500和1 750 s-1。试验前测量好试样及压杆尺寸,并且为防止试样与压杆间产生摩擦而影响试验结果,需要在试样上涂抹黄油。在检查并确认试验准备无误的情况下进行试验,为保证试验数据的可靠,每组试验重复3次以上(Chen et al.,2013; Woo et al.,2013; 张道海等,2014; Qin et al.,2013; Meyers,2006)。通过对应变率为1 250,1 500和1 750 s-1时的试验获取的波形曲线进行处理,得到在室温条件下不同应变率木橡胶减震器的动态压缩应力-应变曲线。
2 结果与分析 2.1 木橡胶减震器的动态压缩结果分析通过观察木橡胶减震器动态压缩试验所得的试验曲线(图 4),发现木橡胶减震器试样可产生较大变形,并且对应变率比较敏感。
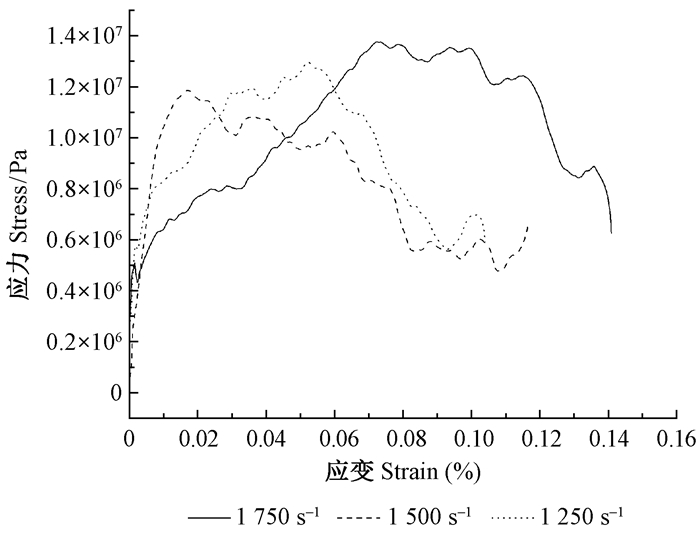 |
图 4 木橡胶减震器的动态压缩应力-应变曲线 Fig. 4 Wood rubber shock absorber dynamic |
对应变率为1 250,1 500和1 750 s-1时的木橡胶减震器应力-应变关系进行分析,可以发现在应变率为1 250 s-1时木橡胶试样的弹性比较理想,屈服强度约为9 MPa,并且明显地表现出木橡胶材料强而韧的特点。应变率为1 250,1 500和1 750 s-1时的流动应力最大值分别为13,12和13.8 MPa,远大于目前常被用来减震的氯丁橡胶的最大许用应力,氯丁橡胶在室温下应变率为1 000~2 000 s-1时的流动应力最大值小于7 MPa(王宝珍等,2007)。虽然在被破坏前氯丁橡胶能够产生的形变比木橡胶大,但木橡胶的韧性要比氯丁橡胶好得多,并且在应变相同的情况下,木橡胶比氯丁橡胶吸收的能量多。 海绵橡胶是海绵状多孔结构的硫化橡胶,广泛用作隔音、防震材料,在准静态压缩条件下,泡沫橡胶对应变率反应不敏感,且500~2 000 s-1时的流动应力最大值为0.3 MPa,而且表现出软而韧的特点(庞宝君等,2011)。通过与木橡胶比较,可知木橡胶比泡沫橡胶的韧性及能量吸收的能力要好得多,但是泡沫橡胶能够产生更大的变形。
2.2 木橡胶减震器的动态压缩后损伤行为1)宏观观察 图 5为木橡胶减震器经动态压缩后的形态,可以看出木橡胶减震器的变形随着应变率的升高而增大,并且在应变率1 500 s-1时木橡胶减震器出现了45°的表面裂纹,裂纹形态如图 6所示。
 |
图 5 木橡胶减震器动态压缩后形态 Fig. 5 Wood rubber shock absorber dynamic compressed morphology |
 |
图 6 木橡胶减震器裂纹形态 Fig. 6 Wood rubber shock absorber crack morphology |
2)微观观察 通过观察木橡胶减震器动态压缩后的微观破坏形貌(图 7),可以发现制备的木橡胶减震器在3种应变率下破坏形式主要是胶的破坏,这是因为受到高应变率冲击的木橡胶减震器部分区域温度会升高很多,致使受到外力作用下的木橡胶减震器软化的胶被拉长。
 |
图 7 木橡胶减震器动态压缩后的微观破坏形貌 Fig. 7 Micro damage morphology of wood rubber shock absorber dynamic compressed a.1 250 s-1; b.1 500 s-1; c.1 750 s-1. |
木橡胶减震器试样中胶产生破坏的同时,木纤维也发生了不同程度的破坏,但是所产生的破坏并不严重。以应变率为1 250 s-1时的试样为例,图 7a清楚地展现了木橡胶减震器试件裂纹处部分木纤维产生了裂痕。
木橡胶减震器试样裂痕处胶破坏时产生的软化效应随着温度的降低部分被破坏的胶又凝结成球状。
3 木橡胶减震器Johnson-Cook型本构方程 3.1 Johnson-Cook型本构方程简介Johnson-Cook型本构方程是一种率相关的经验型本构模型,主要考虑流动应力的应变率效应,具有表达形式简单、参数较少、通用性强、使用方便等特点,常被用来描述材料受冲击载荷作用后的动态力学性能。本文旨在用Johnson-Cook模型描述木橡胶材料的本构关系,并通过对比Johnson-Cook型本构曲线与试验曲线的吻合程度来检验所求得的Johnson-Cook型本构方程对木橡胶减震器应力与应变关系的描述是否准确(张燕等,2012; 王文涛等,2012; Johnson et al.,1983; Zhu et al.,2010)。
Johnson-Cook型本构方程为:
| ${\sigma _{\rm{e}}} = [A + B{({\varepsilon _{\rm{e}}}^{\rm{p}})^n}] \times [1 + Cln(\dot \varepsilon )] \times [1 - {T^{*{\rm{m}}}}]\;。 $ | (1) |
式中:σe为VonMises流动应力(Von Mises 流动应力是基于剪切应变能的一种等效应力,作为衡量应力水平的主要指标,常用来描绘联合作用的复杂应力状态,其值为 {[(a1-a2)2+(a2-a3)2+(a3-a1)2]/2}0.5,其中a1,a2,a3分别指第一、二、三主应力);εpe为等效塑性应变;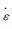 * 为塑性应变率(
* 为塑性应变率(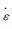 *=
*=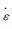 /
/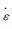 0,其中,
0,其中,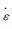 为等效塑性应变率,
为等效塑性应变率,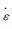 0 为Johnson-Cook型本构关系的参考应变率,一般取10-3s-1); T* 为无量纲化的温度(T*=T-Tσr/Tσm-Tσr,其中,T为试验温度,Tσr 为参考温度,Tσm 为材料的熔点); A,B,C,n,m为待定参数(A为屈服强度,B,n为应变的强化系数,C为应变率的敏感系数,m为温度软化系数)。
0 为Johnson-Cook型本构关系的参考应变率,一般取10-3s-1); T* 为无量纲化的温度(T*=T-Tσr/Tσm-Tσr,其中,T为试验温度,Tσr 为参考温度,Tσm 为材料的熔点); A,B,C,n,m为待定参数(A为屈服强度,B,n为应变的强化系数,C为应变率的敏感系数,m为温度软化系数)。
本文是在室温下进行木橡胶减震器动态压缩试验,因此不用考虑温度软化的影响,Johnson-Cook型本构方程变为:
| $ {\sigma _{\rm{e}}} = [A + B{({\varepsilon _{\rm{e}}}^{\rm{p}})^n}] \times [1 + Cln({\dot \varepsilon ^ * })]。$ | (2) |
1)参数A,B,n的确定 取 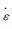 0=1×10-3,根据应变率为1×10-3s-1时的应力-应变曲线确定参数A,B,n,此时
0=1×10-3,根据应变率为1×10-3s-1时的应力-应变曲线确定参数A,B,n,此时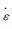 *=1,ln(
*=1,ln(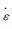 *)=0,Johnson-Cook型本构方程变为:
*)=0,Johnson-Cook型本构方程变为:
| $ {\sigma _{\rm{e}}} = [A + B{(\varepsilon )^n}]\;。$ | (3) |
式中: A为木橡胶材料在应变率为1×10-3s-1时的屈服强度,通过观察木橡胶减震器在应变率为1×10-3s-1时的应力-应变曲线(图 8),可以发现该材料没有明显的屈服点,因此取木橡胶减震器试样产生0.2塑性应变时的应力21 MPa作为屈服强度(李建光等,2012; 常列珍等,2010),即A=21 MPa。
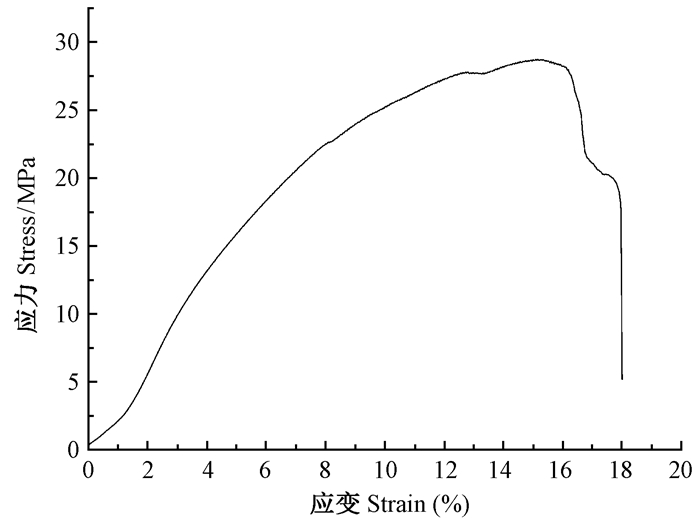 |
图 8 应变率为1×10-3s-1时的应力-应变曲线 Fig. 8 The strain rate is 1×10-3s-1 of the stress-strain curve |
将A值带入式(3),并将等式两边取对数,可得方程为:
| $\ln (\sigma - 21) = \ln (B) + n\ln (\varepsilon )\;。 $ | (4) |
由美国Origin Lab公司开发的Origin软件在数据制图和数据分析方面功能强大,并且具有简单、直观、精确等特点。本文利用Origin软件将试验所得应力-应变曲线转换为 ln(σ-21)-ln(ε)曲线,并通过公式 Y=A+BX 进行拟合。通过观察表 1及图 9可以发现曲线的拟合效果较好,可得B=e-1.11=0.329,n=1.16。
|
|
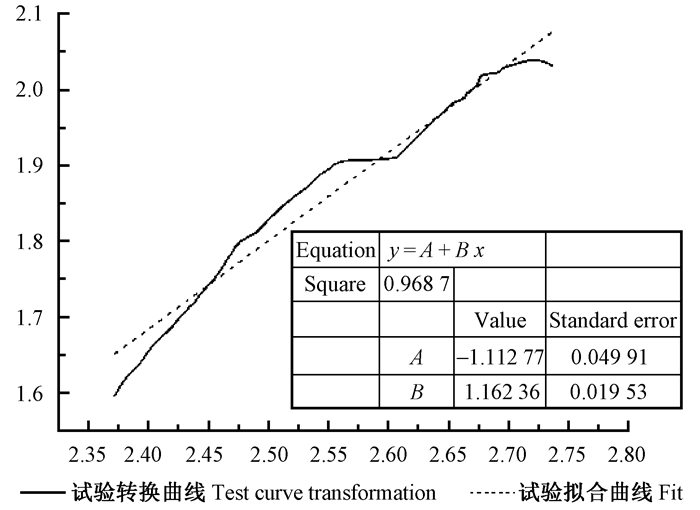 |
图 9 ln(σ-21)-ln(ε)曲线拟合结果 Fig. 9 The results of ln(σ-21)-ln(ε)curve fitting |
2)参数C的确定 将A,B,n带入式(2),可得方程为:
| $\sigma = [21 + 0.329{(\varepsilon )^{1.16}}] \times [1 + C\ln ({\dot \varepsilon ^*})]\;。 $ | (5) |
取塑性应变ε=0,则式(5)变为:
| $\sigma = 21[1 + Cln({\dot \varepsilon ^ * })]\;。 $ | (6) |
可以看出 σ与ln( *)为线性关系,通过最小二乘法对参数C进行拟合,得到拟合公式为:
*)为线性关系,通过最小二乘法对参数C进行拟合,得到拟合公式为:
| $C = \frac{{\sum\limits_{i = 1}^3 {({\sigma _i}/A - 1) \times ln({{\dot \varepsilon }_i}^ * )} }}{{\sum\limits_{i = 1}^3 {{{[ln({{\dot \varepsilon }_i}^ * )]}^2}} }}\;。 $ | (7) |
i =1,2,3分别对应应变率为1 250,1 500和1 750 s-1时的状态,参考应变率选取10-3s-1,即ε·0=0.1 s-1,通过计算可得C≈0.148。
因此得木橡胶减震器在室温条件下的Johnson-Cook型本构方程为:
| $\sigma = [21 + 0.329{(\varepsilon )^{1.16}}] \times [1 + 0.148\ln ({\dot \varepsilon ^*})]\;。 $ | (8) |
利用Origin软件求得Johnson-Cook型本构方程的拟合曲线,与试验曲线进行对比,得到木橡胶减震器试验曲线与Johnson-Cook型本构方程拟合曲线对比图如图 10所示。
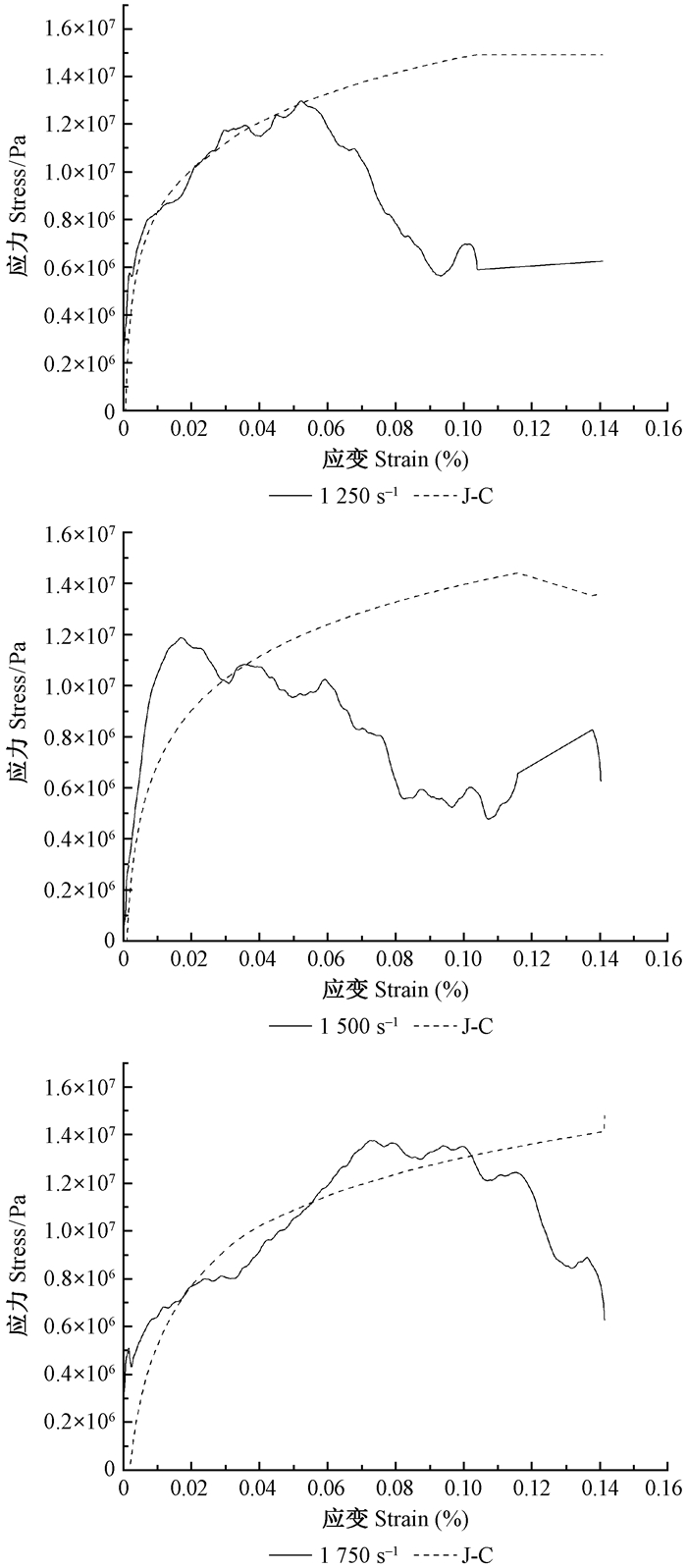 |
图 10 木橡胶减震器试验曲线与Johnson-Cook型本构方程拟合曲线对比 Fig. 10 The comparison of wood rubber shock absorber experiment curves and Johnson-Cook constitutive equation fitting curve |
通过观察图 10可以发现,应变较小时Johnson-Cook型本构方程拟合效果较好。其中,应变率为1 250 s-1时Johnson-Cook型本构方程拟合效果最好,当应变小于0.056时,拟合值与试验值几乎完全吻合; 应变率为1 500 s-1时,Johnson-Cook型本构方程低估了木橡胶减震器的流动应力,而且随着应变的增加,拟合值与试验值相差变大,拟合效果不够理想; 应变率为1 750 s-1时,应变大小在0.025,0.05,0.1附近时Johnson-Cook型本构方程拟合值效果好。总体来说,在应变较小时所求Johnson-Cook型本构方程与试验曲线拟合比较理想。为了得到更准确的木橡胶减震器Johnson-Cook型本构关系,今后还需要对Johnson-Cook型本构方程的参数进行优化,并进行大量试验验证。
4 结 论本文选用由小兴安岭红松木块加工而成的微米木丝及氯丁胶制备木橡胶减震器试样,并利用分离式霍普金森压杆在室温下对其进行动态压缩试验,通过分析试验结果得知,木橡胶减震器对应变率比较敏感,能够实现较大的变形,在3种应变率下的最大流动应力较高,均大于12 MPa,远远超过目前较广泛应用于减震的氯丁橡胶的最大许用应力,并且木橡胶的韧性及吸收能量的性能要比氯丁橡胶好。
通过观察试验后试样微观损伤,发现木橡胶减震器的失效形式大部分为胶的失效,因此,当制备木橡胶减震器时应选用与微米木丝的强度接近的胶,从而使木橡胶减震器力学性能更佳。
利用木橡胶减震器动态压缩的试验数据及Origin软件,确定了Johnson-Cook型本构方程的参数,初步得到室温下该型的本构方程:σ=[21+0.329ε1.16]×[1+0.148ln( *)] 。对比求得的本构方程拟合曲线与试验曲线后发现,应变较小时,求得的本构方程对木橡胶减震器应力与应变关系的描述比较准确,其中应变率为1 250 s-1且应变小于0.056时,求得的本构方程拟合值与试验值几乎完全吻合。
*)] 。对比求得的本构方程拟合曲线与试验曲线后发现,应变较小时,求得的本构方程对木橡胶减震器应力与应变关系的描述比较准确,其中应变率为1 250 s-1且应变小于0.056时,求得的本构方程拟合值与试验值几乎完全吻合。
| [1] |
常列珍,潘玉田,张治民. 2010.一种调制50SiMnVB钢Johnson-Cook本构模型的建立.兵器材料科学与工程,33(4):68-72. (Chang L Z,Pan Y T,Zhang Z M. 2010. Johnson-Cook constitutive model for hardened and tempered 50SiMnVB steel. Ordnance Material Science and Engineering,33(4):68-72[in Chinese]).(  1) 1)
|
| [2] |
李建光,施琪,曹续东. 2012. Johnson-Cook本构方程的参数标定.兰州理工大学学报,38(2):164-167. (Li J G,Shi Q,Cao X D. 2012. Parameter calibration for Johnson-Cook constitutive equation. Journal of Lanzhou University of Technology,38(2):164-167[in Chinese]).(  1) 1)
|
| [3] |
马岩,潘承怡. 2008.微米木纤维模压制品形成的试验装备与工艺.林业科学,44(6):113-117. (Ma Y,Pan C Y. 2008. Experimental equipment and technology of forming micron wood fiber mould product. Scientia Silvae Sinicae,44(6):113-117[in Chinese]).(  1) 1)
|
| [4] |
马岩,袁旭,孙奇,等. 2014.微米木丝车用木橡胶减震器模压工艺及制备.安徽农业科学,42(14):4309-4311. (Ma Y,Yuan X,Sun Q,et al. 2014. The process methods and fabrication of micron wood fiber molding vehicle wooden rubber shock absorbers. Journal of Anhui Agri Sci,42(14):4309-4311[in Chinese]).(  2) 2)
|
| [5] |
马岩. 2003.利用微米木纤维定向重组技术形成超高强度纤维板的细胞裂解理论研究.林业科学,39(3):111-115. (Ma Y. 2003. Study on cell break theory of using wood fibre micro-meter aligned reconstituted technology forming super high-intensity wood-based panel. Scientia Silvae Sinicae,39(3):111-115[in Chinese]).(  1) 1)
|
| [6] |
庞宝君,杨震琦,王立闻,等. 2011.橡胶材料的动态压缩性能机应变率相关的本构模型.高压物理学报,25(5):409-415. (Pang B J,Yang Z Q,Wang L W,et al. 2010. The constitutive model of dynamic compression performance machine strain rate dependency of the rubber material. Chinese Journal of High Pressure Physics,25(5):409-415[in Chinese]).(  1) 1)
|
| [7] |
王宝珍,胡时胜,周相荣. 2007.不同温度下橡胶的动态力学性能及本构模型研究.实验力学,22(1):1-6. (Wang B Z,Hu S S,Zhou X R. 2007. Dynamic mechanical properties of rubber and constitutive model at different temperatures. Journal of Experimental Mechanics,22(1):1-6[in Chinese]).(  1) 1)
|
| [8] |
王文涛,上官文斌,段小成. 2012.超弹性本构模型对橡胶隔振器静态特性预测影响的研究.汽车工程,34(6):544-550. (Wang W T,Shangguan W B,Duan X C. 2012. A study on the effects of hyperelastic constitutive models on the static characteristic prediction of rubber isolator. Automotive Engineering,34(6):544-550.[in Chinese])(  1) 1)
|
| [9] |
杨春梅,吴哲,马岩,等. 2014.木橡胶的动态压缩力学性能及其破坏行为.林业科学,50(12):161-167. (Yang C M,Wu Z,Ma Y,et al. 2014. Dynamic mechanical properties and micro-fracture behavior of wood rubber. Scientia Silvae Sinicae,50(12):161-167[in Chinese]).(  1) 1)
|
| [10] |
袁旭,马岩. 2014.木橡胶的性能及开发利用前景展望.安徽农业科学,42(9):2662-2697. (Yuan X,Ma Y. 2014. The performance and development prospects of wood-based rubber. Journal of Anhui Agri Sci,42(9):2662-2697[in Chinese]).(  1) 1)
|
| [11] |
张燕,宋魁彦,佟达. 2012.复配碱液处理榆木顺纹压缩应力-应变本构关系.林业科学,48(11):83-86. (Zhang Y,Song K Y,Tong D. 2012. Stress-strain constitutive relations of longitudinal compressed elm wood with compound alkali liquor processing. Scientia Silvae Sinicae,48(11):83-86[in Chinese]).(  1) 1)
|
| [12] |
张道海,何敏,郭建兵,等. 2014.高强度聚甲醛复合材料的动态力学性能.胶体与聚物,32(1):14-17. (Zhang D H,He M,Guo J B,et al. 2014. Dynamic mechanical properties of high strength polyoxymethylene composite. Chinese Journal of Colloid & Polymer,32(1):14-17[in Chinese]).(  1) 1)
|
| [13] |
Chen X,Wu S,Zhou J. 2013. Experimental and modeling study of dynamic mechanical properties of cement paste, mortar and concrete. Construction and Building Materials, 47:419-430.( 1) 1)
|
| [14] |
Johnson G R,Cook W H. 1983. A constitutive model and data for metals subjected to large strains,high strain rates and high temperature.Proceedings of the Seventh International Symposium on Ballistics, Netherland.( 1) 1)
|
| [15] |
Meyers M A. 2006. Dynamic behavior of materials. Beijing:National Defence Industry Press,225-260.( 1) 1)
|
| [16] |
Qin J,Chen R,Wen X,et al. 2013. Mechanical behaviour of dual-phase high strength steel under high strain rate tensile loading. Materials Science and Engineering, 586:62-70.( 1) 1)
|
| [17] |
Woo S C,Kim J T,Cho C H,et al. 2013. The dynamic compressive behavior of armor structural materials in split Hopkinson pressure bar test. Journal of Strain Analysis for Engineering Design,48(7):420-436.( 1) 1)
|
| [18] |
Zhu J S,Hu J M,Wang P,et al. 2010. A review on research progress in explosion mechanics and impact dynamics. Advance in Mechanics,40(4):400-423.( 1) 1)
|
 2015, Vol. 51
2015, Vol. 51

