文章信息
- 付甜, 朱建华, 肖文发, 曾立雄
- Fu Tian, Zhu Jianhua, Xiao Wenfa, Zeng Lixiong
- 八种亚热带森林类型乔木层地上生物量分配模型
- Above-Ground Biomass Distribution Models for Arbor Layer of Eight Subtropical Forest Types
- 林业科学, 2014, 50(9): 1-9
- Scientia Silvae Sinicae, 2014, 50(9): 1-9.
- DOI: 10.11707/j.1001-7488.20140901
-
文章历史
- 收稿日期:2013-05-24
- 修回日期:2014-08-01
-
作者相关文章
森林是陆地生态系统中最大的碳库,森林生态系统的碳储量占到整个地球陆地生态系统碳储量的50%以上(Dixon et al., 1994)。在区域和国家尺度,各国通常利用森林资源清查资料如森林面积、蓄积量等,结合生物量方程或生物量碳计量参数,估算各时期的森林生物量及其碳储量动态变化。中国具有系统完整的森林资源清查数据,已有不少将森林资源清查数据的蓄积量转化为生物量的模型方法方面的研究(冯仲科等,2005)。常用生物量估算方法如IPCC(政府间气候变化专门委员会)法、转换因子连续函数法、加权生物量回归模型法,这些方法都属于生物量转换因子法(BEF),也称材积源生物量法,是利用林分生物量与木材材积比值的平均值乘以该森林类型的总蓄积量得到该森林类型总生物量的方法,在精度要求不高的情况下应用广泛(Fang et al., 2001;方精云等,2002;李海奎等,2011)。虽然蓄积量资料提供了森林材积的准确信息,但生物量转换因子如木材密度均取常数,由此去推算生物量不确定性极高。另外,在森林生物量的组成当中,树干(材积)只是其中的一部分,其在林分中所占的比率因树种和立地条件不同而有很大的差异(Brown et al., 1984)。有研究表明,树干的生物量与其他器官的生物量存在很强的相关关系(Whittaker et al., 1975),可见由树干材积推算树干生物量,再推及其他器官的生物量是可行的。但是干、皮、枝和叶4部分干质量之和不等于总生物量的问题一直未得到很好地解决,有研究采用线性联立方程或非线性联合估计模型2种解决方案来解决相容性的问题(胥辉,1999;骆期邦等,1999;唐守正等,2000)。但该方法计算方式复杂,对数据和参数的要求较高,并未能被广泛应用。为避免生物量的估计过于粗放和简单,有必要进一步从地域、树种上精细分类,系统建立生物量与材积的关系模型。
本研究以长江三峡库区的8种主要亚热带森林类型为研究对象,分别采用幂函数模型和多项logit模型建立材积-生物量转换模型以及林分各器官(干、皮、枝和叶)生物量比例模型,为进一步精确计量各林分类型乔木层地上生物量的碳储量及其变化奠定基础。同时研究结果也能丰富我国森林生物量碳计量参数,为其他相关研究提供参考。
1 材料来源长江三峡库区(105°49′-111°39′ E,28°28′-31°44′ N)横跨鄂西、渝东山地,北靠神农架南侧和大巴山东端,南依云贵高原,位于秦岭淮河以南,在长江流域中上青藏高原向中下游平原过渡带上,总面积约5.8万km2。地处亚热带北缘,具明显亚热带湿润性气候特征。对库区内植被做过系统调查和分类(程瑞梅等,1999;肖文发等,2000;曾立雄等,2008),大体可分为8种主要森林类型: 暖温性常绿针叶林,包括马尾松(Pinus massoniana)林柏木(Cupressus funebris)林和杉木(Cunninghamia lanceolata)林;温性常绿针叶林,主要为温性松林;落叶阔叶林,主要为栎(Quercus)类混交林,常绿阔叶林,主要为其他硬阔林;针阔混交林、针叶混交林。其中针叶树种主要有马尾松、杉木、柏木、华山松(Pinus arm and i)和巴山松(Pinus henryi)等;落叶阔叶树以栎属、枫香(Liquidambar formosana)、桦木(Betula)和刺槐(Robinia pseudoacacia)占优;常绿阔叶林则以石栎(Lithocarpus glaber)、青冈(Cyclobalanopsis glauca)和栲(Castanopsis fargesii)为主。
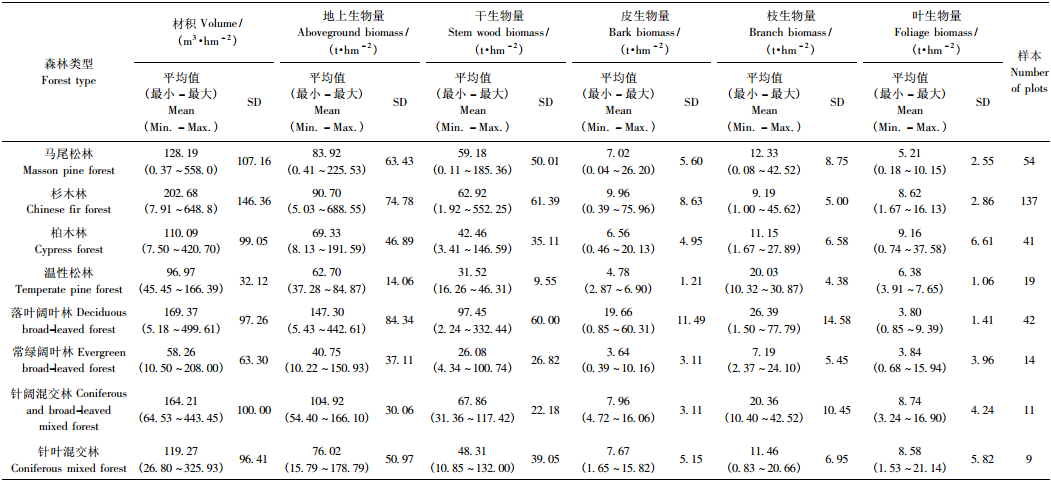
根据已有的分类基础,本研究为保证样本数量达到统计要求,除三峡库区本地的调查数据之外,从文献中收集和整理了样地位置均处于亚热带地区的以上8种森林类型的样地数据,共334块。各森林类型样地概况见表 1。每块样地的调查数据具体包括乔木层公顷材积,公顷生物量,以及干、皮、枝、叶各器官生物量数据,详见表 2。
|
|
|
|
在以往的研究中,根据树高和胸径计算材积和生物量的模型通常都是非线性的,而在利用材积转换生物量的过程中,却采用单一的线性回归模型(王仲锋,2006),如采用材积与木材密度的乘积作为树干生物量,这种简单的线性关系没有考虑林分不同生长阶段木材密度的差异。将同样采用树高和胸径来计算生物量和材积的非线性模型做联合推导,可以观察到生物量和材积之间的联系。
设某一样地内同一树种的乔木总株数为n,平均树高和平均胸径分别为$\bar H$和$\bar D$,则样地内该树种的样地乔木树干生物量W和乔木总材积V(带皮,不包含树桩与树顶,胸径>5 cm,单位为m3·hm-2)用相对生长法估算时,可利用平均断面积法表示为:
| $W = na{\left({{{\bar D}^2}\bar H} \right)^b}$ | (1) |
| $V = na'{\left({{{\bar D}^2}\bar H} \right)^{b'}}$ | (2) |
将上式(1)作变换,可得:
| $\begin{array}{l} W = na{\left[ {\frac{1}{{na'}}na'{{\left({{{\bar D}^2}\bar H} \right)}^{b'}}} \right]^{b/b'}} = \\ \frac{n}{{{{\left(n \right)}^{b/b'}}}} \cdot \frac{a}{{{{\left({a'} \right)}^{b/b'}}}}{\left[ {na'{{\left({{{\bar D}^2}\bar H} \right)}^{b'}}} \right]^{b/b'}} \end{array}$ | (3) |
若令d=b/b′,c=a/(a′)d,则有
| $W = {n^{1 - d}}c{V^d}$ | (4) |
式中:a,a′,b,b′,c和d为参数。
根据以上推论,假设林分树干生物量Ws(不带皮,包含树桩与树顶,单位为t·hm-2)与总材积V的关系方程可以用幂函数表达为:
| ${W_s} = {a_s} \times {V^{{b_s}}}$ | (5) |
式中: as,bs为 非线性模型参数。
对整个林分而言,树干生物量是总地上生物量的主要部分,该幂函数模型将作为计算林分地上总生物量的基础模型。
2.2 林木器官生物量比例模型多项logit模型是二项logit模型的一般形式,二项logit模型作为一种常用的广义线性模型,主要用于二元响应变量的概率建模。在多元响应变量的类别之间不存在序次关系的情况下,可以用多项logit模型来预测各类别的发生概率(饶雄等,2008),其本质是用最大似然估计法将类别特质对类别选择的影响估计出来。多项logit模型一直以来多用于经济学领域的概率估计,应用在生态学上的研究并不多见。该模型的主要优点是容易计算,选择给定类别的概率即比例易于表示,并且保证各项概率之和为1,可以很好地解决总量和各维量的兼容问题。森林碳收支模型CBM-CFS3采用以林分水平的商用材材积为自变量的多项logit模型估算干、皮、枝和叶生物量在林分总地上生物量中所占的比例,本研究拟采用该模型建立林分水平的林木器官比例模型,模型中表达干、皮、枝和叶生物量比例的4个公式如下:
| $\begin{array}{l} {P_s} = 1/\left[ {{e^{{a_1} + {a_2} \times V + {a_3} \times \ln \left({V + 5} \right)}}} \right. + \\ {e^{{b_1} + {b_2} \times V + {b_3} \times \ln \left({V + 5} \right)}} + \\ e\left. {^{{c_1} + {c_2} \times V + {c_3} \times \ln \left({V + 5} \right)}} \right] \end{array}$ | (6) |
| $\begin{array}{l} {P_b} = \left[ {{e^{{a_1} + {a_2} \times V + {a_3} \times \ln \left({V + 5} \right)}}} \right./\\ {e^{{a_1} + {a_2} \times V + {a_3} \times \ln \left({V + 5} \right)}} + \\ {e^{{b_1} + {b_2} \times V + {b_3} \times \ln \left({V + 5} \right)}} + \\ e\left. {^{{c_1} + {c_2} \times V + {c_3} \times \ln \left({V + 5} \right)}} \right]; \end{array}$ | (7) |
| $\begin{array}{l} {P_{br}} = \left[ {{e^{{b_1} + {b_2} \times V + {b_3} \times \ln \left({V + 5} \right)}}} \right./\\ {e^{{a_1} + {a_2} \times V + {a_3} \times \ln \left({V + 5} \right)}} + \\ {e^{{b_1} + {b_2} \times V + {b_3} \times \ln \left({V + 5} \right)}} + \\ e\left. {^{{c_1} + {c_2} \times V + {c_3} \times \ln \left({V + 5} \right)}} \right]; \end{array}$ | (8) |
| $\begin{array}{l} {P_f} = \left[ {{e^{{c_1} + {c_2} \times V + {c_3} \times \ln \left({V + 5} \right)}}} \right./\\ {\left[ e \right.^{{a_1} + {a_2} \times V + {a_3} \times \ln \left({V + 5} \right)}} + \\ {e^{{b_1} + {b_2} \times V + {b_3} \times \ln \left({V + 5} \right)}} + \\ e\left. {^{{c_1} + {c_2} \times V + {c_3} \times \ln \left({V + 5} \right)}} \right]. \end{array}$ | (9) |
式中: Ps,Pb,Pbr和Pf分别为树干、树皮、树枝和树叶生物量占总地上生物量的比例; a1,a2,a3,b1,b2,b3,c1,c2和c3 为模型参数。
多项logit模型通常需要先处理不符合名义变量标准的因变量,为其赋值。在本研究收集到的数据为连续变量的情况下,为简化数据处理过程,对式(6)~(9)构成的方程组进行联立估计。在用林分材积求得树干生物量的前提下,用求得的干、皮、枝和叶器官的生物量比例,可进一步求得林分地上总生物量以及各器官的生物量。
2.3 模型评价与精度检验本研究评价模型优劣的主要3个指标为: 1)决定系数R2 检验模型拟合优度,R2值越大,因变量与自变量之间地相关性越强;2)均方根误差(RMSE)RMSE越小,预测效果越好;3)显著性检验(P值)P≤0.05显著,P<0.001极显著。
均方根误差的计算公式为:
| ${\rm{RMSE = }}\sqrt {\frac{{\sum {{{\left({y - {y_c}} \right)}^2}} }}{n}} $ | (10) |
式中: y为观测值;yc为预测值,n为建模样本数目。
模型拟合时,随机留取10%的样本用于精度检验,计算抽检样本的预测精度,分析模型预测效果,精度计算见下式:
| $P = 1 - {\rm{MAPE = }}\left({1 - \frac{1}{m}\sum {\frac{{\left| {y - {y_c}} \right|}}{y}} } \right)\times 100\% $ | (11) |
式中: MAPE为平均相对误差绝对值,m为检验样本数目。
3 结果与分析 3.1 材积—生物量转换采用非线性回归中的幂函数对林分水平的树干生物量与材积进行曲线拟合,拟合效果见图 1(以杉木林为例)。各森林类型数据分析与参数结果详见表 3。结果表明: 林分树干生物量与总材积表现出极强的相关性,预测值与实测值间的残差呈正态分布,残差随总材积增加而增加。各森林类型的拟合结果均较为理想,其中,落叶阔叶林的R2最高,达到0.984;常绿阔叶林的相关性不显著(P>0.05),R2仅为0.232,其他森林类型均达到极显著水平(P<0.001),R2则均大于0.5(0.575~0.934)。均方根误差RMSE对特大和特小误差极为敏感,能很好地反映预测的准确性。温性松林的RMSE最小,仅为6.520 t·hm-2,其他森林类型的RMSE结果表现为针阔混交林7.415 t·hm-2<杉木林10.706 t·hm-2<落叶阔叶林11.811 t·hm-2<柏木林13.473 t·hm-2<马尾松林19.939 t·hm-2<常绿阔叶林23.123 t·hm-2。
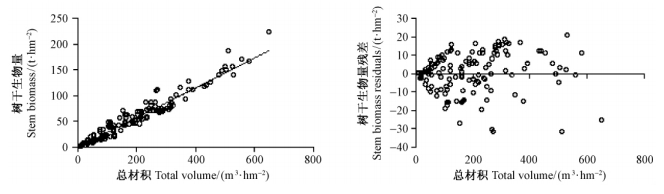 |
图 1 材积-生物量转换模型拟合效果(杉木林) Fig. 1 Results of volume-to-biomass conversion model(Chinese fir forest) |
多项logit模型的拟合效果见图 2(以杉木林为例),参数结果详见表 4。林分中各分量占总地上生物量的比例与林分总材积表现出极强的相关性,干、皮生物量的比例随林分材积的增大而增加,而枝、叶生物量比例的变化趋势则相反,随林分材积的增大而减少。预测值与实测值间的残差呈正态分布,残差随总材积增加而减小。所有森林组分的比例中树干生物量的R2最高,达到0.314~0.809;皮、枝、叶生物量的R2较之略低,分别达到0.019~0.477,0.180~0.709和0.025~0.818。马尾松林、杉木林、柏木林和落叶阔叶林的预测值与实测值极显著相关(P<0.001),温性松林、针阔混交和针叶混交林显著相关(P<0.05),常绿阔叶林的结果为相关性不显著。拟合后的RMSE均控制在合理范围内,其中干生物量比例的RMSE不超过0.09,为0.031~0.085;皮、枝和叶生物量在整个林分中占有的比例较低,故它们的RMSE显得略高,分别达到0.005~0.041,0.029~0.103和0.016~0.083。从整体的拟合效果来看,杉木林结果最优,其干、枝、叶生物量比例模型的R2均超过0.6;常绿阔叶林结果最差,R2与RMSE均不理想。
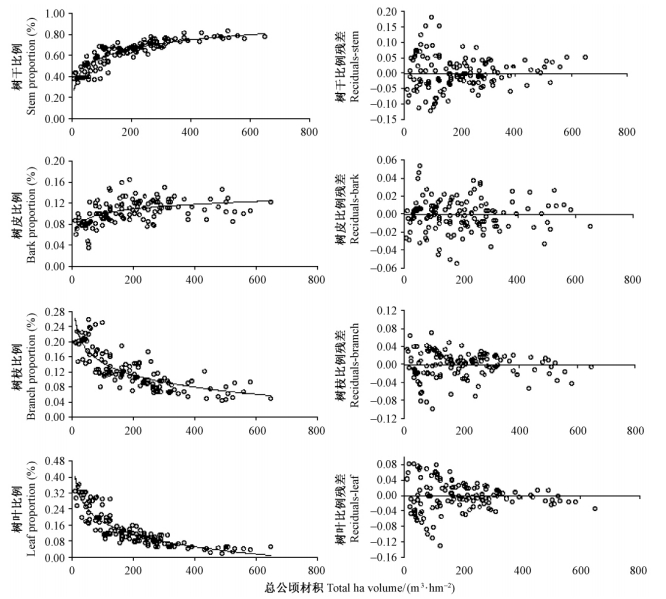 |
图 2 林木器官生物量比例模型拟合效果(杉木林) Fig. 2 Results of proportion models for biomass components(Chinese fir forest) |
|
|
|
|
精度检验的结果见表 5。采用材积转换为树干生物量的预测精度为31.14%~91.79%,除常绿阔叶林外,其他森林类型的预测精度均达到70%以上。林木器官生物量比例的预测结果中,干生物量比例的预测精度最高,均达到91%以上;皮、枝生物量比例的预测精度略低,分别达到62.71%~94.48%和63.70%~94.47%;叶生物量比例的估计结果最不稳定,预测精度为-8.86%~83.92%。常绿阔叶林的预测效果不佳,温性松林的比例预测精度最优。
|
|
从材积-生物量转换模型的拟合效果来看,材积与生物量的关系良好,除常绿阔叶林外,预测精度均高于70%,可采用幂函数进行材积与生物量之间的转换。模型预测效果由高至低为: 针阔混交林>落叶阔叶林>温性松林>杉木林>柏木林>马尾松林>常绿阔叶林。
从林分生物量器官比例模型的拟合结果可以看出,除常绿阔叶林外,各森林类型的模型拟合效果良好,多项logit模型对干生物量比例的预测精度高于91%,对皮、枝和叶生物量比例的预测较不稳定,但不影响模型的兼容性。各树种的模型预测效果表现为杉木林>落叶阔叶林>温性松林>针叶混交林>马尾松林>柏木林> 针阔混交林>常绿阔叶林。本研究所得各森林类型(除常绿阔叶林外)的乔木层地上生物量模型合理,其预测结果能获得较高的精度。
要辨明一个模型是否合理,需要保证F统计值显著(P≤0.05),且预测值和残差表现出合理的趋势。如果有一个或更多的标准未能达到,该模型就应该放弃。本研究中拟合的模型中只有常绿阔叶林没有达到显著水平,这可能跟该森林类型的样本数目过少,林分树种组成太复杂有关。其他森林类型模型的拟合效果较好,且相关性显著,误差结果也处于合理范围,总体比较理想。目前,虽然生物量的方法和技术在不断改进,研究的尺度也更多变,但是对于不同年龄林分的生物量分布及分配规律的相关研究并不多。植物各器官生物量分配是动态变化的,尤其生长初期,生物量分配模式将最大可能地影响植物的未来的碳分配(巨文珍等,2011)。在多项logit模型拟合过程中,存在的主要问题是数据缺失或存在混合样本。模型拟合结果表明皮、枝、叶生物量的比例与材积之间的关系强度远不及树干,相关系低于理想值,特别是对皮的比例的预测效果最差。但是,树干生物量在地上总生物量中所占的比重最大,一般占到地上生物量的60%以上,树皮生物量则在地上总生物量中占有最小的比例,皮、枝和叶比例的预测误差对总生物量的预测影响不大。采用多项logit方法对林木器官的生物量比例进行估算仍然是可行而且相对简单的一种方法。
无论是经验模型亦或是过程模型,模型的适用性问题始终都是不可避免的,因为如要得到精确的生物量计算结果并不是所有地区或每个树种都适用同一套参数,生态环境的复杂性使得研究者更慎重应用模型参数。在精度要求很高的应用条件下,想要得到不同地区的更为精确的计算结果,森林分类条件就需要设得更为详细(例如加入立地条件等),每个分类都应该计算相对应的参数。如要对同一树种进行深入研究,则可能需加入包括同一树种不同地理种源、不同发育阶段、不同自然地带的生物量差异等条件,以及建立生物量树种权重指标体系,实现对生物量较为精确的估测。因此,根据不同的需要,工作量的多少也有差别。本研究中收集到的用于分析的树种样本属于亚热带森林区域,所以得到的各森林类型的模型参数适用于亚热带森林区域,可用于大尺度的碳储量估算研究。
森林中既包含活立木,也包含死木(枯立木或倒木)。尽管死木的生物量限制了生物量经验模型的发展,但在做样地调查时一般会考虑测量相应的死木。用活立木树干生物量比例得到整个林分的生物量,死木的比例也可以用类似的算法获得。但是,由于不健康的树或者倒木在调查中通常不会去记录,结果是低估死木生物量,这部分的比例最好不采用;相对的,样地可能会受到虫灾或其他自然灾害的强烈干扰,造成死木生物量的高估,无论怎样结果都会有很大的误差。因此,是否要估计死木的生物量应当慎重考虑。灌木层,草本层生物量也是同样的道理。
| [1] |
程瑞梅,肖文发,李建文,等. 1999.三峡库区森林植被分类系统初探. 环境与开发, 14 (2): 4-8.( 1) 1)
|
| [2] |
方精云,陈平安,赵淑清,等. 2002.中国森林生物量的估算: 对Fang等Science一文(Science, 2001,291:2320-2322)的若干说明.植物生态学报,26(2): 243-249.( 1) 1)
|
| [3] |
冯仲科,罗旭,石丽萍. 2005. 森林生物量研究的若干问题及完善途径.世界林业研究, 18(3): 25-28.( 1) 1)
|
| [4] |
巨文珍,王新杰,孙玉军. 2011. 长白落叶松林龄序列上的生物量及碳储量分配规律. 生态学报,31(4): 1139-1148.( 1) 1)
|
| [5] |
李海奎,雷渊才,曾伟生. 2011. 基于森林清查资料的中国森林植被碳储量. 林业科学,47(7): 7-12.( 1) 1)
|
| [6] |
骆期邦,曾伟生,贺东北,等. 1999. 立木地上部分生物量模型的建立及其应用研究.自然资源学报, 14(3): 271-277.( 1) 1)
|
| [7] |
饶雄,张景雄,丁翼星. 2008. 基于多项logit模型的土地覆被分层分类方法研究. 武汉大学学报: 信息科学版, 33(11): 1166-1169.( 1) 1)
|
| [8] |
唐守正,张会儒,胥辉. 2000. 相容性生物量模型的建立及其估计方法研究. 林业科学,36(Sp.1): 19-27.( 1) 1)
|
| [9] |
王仲锋. 2006. 森林生物量建模与精度分析.北京: 北京林业大学博士学位论文.( 1) 1)
|
| [10] |
胥辉. 1999. 一种与材积相容的生物量模型. 北京林业大学学报,21(5):32-36.( 1) 1)
|
| [11] |
肖文发,李建文,于长青,等. 2000.长江三峡库区陆生动植物生态. 重庆: 西南师范大学出版社, 5-11.( 1) 1)
|
| [12] |
曾立雄,王鹏程,肖文发,等. 2008.三峡库区主要植被生物量与生产力分配特征. 林业科学, 44(8): 16-22.( 1) 1)
|
| [13] |
Brown S, Lugo A E. 1984. Biomass of tropical forests: a new estimate based on forest volumes. Science, 223(4642): 1290-1293.( 1) 1)
|
| [14] |
Dixon R K, Brown S L, Houghton R A, et al. 1994. Carbon pools and flux of global forest ecosystems. Science, 263(5144): 185-190.( 1) 1)
|
| [15] |
Fang J, Chen A, Peng C, et al. 2001. Changes in forest biomass carbon storage in China between 1949 and 1998. Science, 292(5525): 2320-2322.( 1) 1)
|
| [16] |
Whittaker R H, Likens G E. 1975. Methods of assessing terrestrial productivity. New York: Springer-Verlag, 305-328.( 1) 1)
|
 2014, Vol. 50
2014, Vol. 50