近十几年，无损检测技术被广泛用于评价活立木(或原木)质量和内部缺陷，也被用于判定板材等级(王立海等，2008； 梁善庆等，2008； 罗彬等，2008； 苗媛媛等，2008)。研究表明，木材无损检测对科学营林、森林健康监测、原木分等和板材分级等具有重要意义。

多种无损检测手段已被用于木材检测领域，如应力波、超声波、工业CT等，其中超声波法是近年来应用比较广泛的方法之一(苗媛媛等，2008； 徐华东等，2011a； Ozyhar et al., 2013)。与应力波技术相比，超声波具有准确性更高、能量高、信号携带信息更丰富等优点(杨慧敏等，2010)； 与X射线等放射线技术相比，超声波具有无电离辐射、操作简单、便携等优点。应力波层析成像准确率较低，对原木内部腐朽位置定量辨识精度不够； 而基于X射线的层析成像技术准确性很高，但是其设备较大，无法满足木材检测中便携的要求。近年，基于超声波的原木内部腐朽层析成像技术成为研究热点之一，但至今该技术仍无实质性突破。

尽管超声波技术存在信号易受外界干扰、传感器与被测材料的耦合性难以保证等问题(林兰英等，2007; Krause et al., 2013)，但若被测木材是新鲜的(活立木或新伐倒木等)，此时在被测木材与探头圆锥体间之间含有木浆，这样即使不采用耦合剂，也能保证较好的耦合效果(于文勇等，2006)。传统检测每次只对单个超声波信号进行分析，然后基于单个超声信号所提取的特征值对木材缺陷或性质进行评估，既费时间，判断又不准确。支持向量机(support vector machine，SVM)可同时分析多个数据(任俊等，2005； Wang et al., 2008； 曾联明等，2009)，将其与超声波相结合，能够弥补传统超声检测的不足，检测结果更可信。

本文通过对完好和含孔洞原木圆盘进行超声检测，提取信号特征值，利用支持向量机对孔洞大小和位置进行判别。在此基础上，利用Matlab软件将缺陷辨识结果绘制在二维平面内，结合图像处理，探讨构建原木内部缺陷二维超声层析图像的方法。

材料为紫椴(Tilia amurensis)原木圆盘，直径34 cm，厚5 cm。在实验室，采用烘干法测定试样含水率，数值为95%。超声波易受含水率影响(Sandoz， 1993； 徐华东等，2011b; Hasegawa et al., 2011)，因此将圆盘密封低温(0～5 ℃)保存，防止水分流失。测试时，取出试样，在15 ℃下测试约30 min，然后立即低温保存。原木是指伐倒的树干经打枝和造材后的木段。本文选用圆盘小试样进行试验，主要是为了便于在实验室中研究原木横截面超声二维成像方法，为以后原木现场木材检测做前期基础。

采用RSM-SY5超声波仪测试原木横截面内的超声波信号。将圆盘周长等分30份，在三等分点分别标记点1、点11和点21，如图 1。测试时，分别以这3点为发射点，在完好样本横截面上量取距离大于33 cm的位置(重点研究距离在33～34 cm间的超声信号，因为后续所制圆孔在此测试范围内)若干作为接收点，测试并记录每个接收点接收到的超声信号，保存数据。然后，对圆盘制孔，孔径d分别为4，6，8和10 cm。制孔后，在不同孔径下分别进行超声测试，测试过程与完好时一致，记录并保存缺陷数据。

	图1 超声波测点示意 Fig.1 Illustration of ultrasonic wave testing point

对超声信号首波进行特征值提取，包括振幅、起始时间、周期、半波周期、上升时间、下降时间和平均传播速度。利用完好试样的32个超声数据与含孔洞(d=4，6，8和10 cm)试样91个数据作为数据集，分析缺陷大小对超声波传播特性的影响。利用SVM对数据集进行分类，判别孔洞大小。分类过程为： 1)选定训练集和测试集； 2)对测试集进行初步预测； 3)惩罚参数c和g的优化选择； 4)利用最佳参数进行SVM网络训练； 5)利用Matlab，将测试集的实际分类和预测结果展现出来。

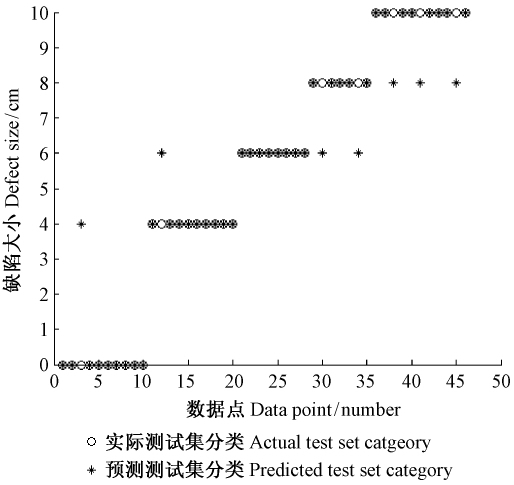
图 2是测试集实际分类和预测结果，其中，圆圈代表实际测试集分类，星号代表预测测试集分类，二者重合表明预测正确，反之则预测错误。由图 2可知，对第1类(d=0 cm)、第2类(d=4 cm)、第3类(d=6 cm)、第4类(d=8 cm)和第5类(d=10 cm)数据的错误预测个数分别为1，1，0，2，3，预测准确率为84.78%，分类结果较理想，表明SVM用于原木孔洞大小分类是可行的。

	图2 测试集实际分类和预测结果分布 Fig.2 Distribution of real and predicting classification result

利用SVM辨识超声信号并进行分类后，再用Matlab软件将辨识结果绘制在二维平面内，以定位缺陷。首先，确定坐标系平面。在样本横截面上，以信号发射点11为原点，以点11到点26的连线为y轴，其垂线为x轴，建立二维平面坐标系。然后，确定坐标系平面内各点的坐标值。在横截面内，分别以点1，11和21为起始点，以圆盘圆周上其他点为终止点进行连线，各连线交点的坐标值即可确定。例如当d=10 cm，以点1和点11为发射点时，实际经过孔洞的直线及其交点的坐标值如表 1。

表1 当点1和点11为发射点时，用于支持向量机判断的经过孔洞(d=10 cm)直线交点的坐标值 Tab. 1 The coordinate values of intersection point of line through the hole with a diameter of 10 cm when point 1 and 11 are driving point respectively

表 1当点1和点11为发射点时，用于支持向量机判断的经过孔洞(d=10 cm)直线交点的坐标值 Tab.1The coordinate values of intersection point of line through the hole with a diameter of 10 cm when point 1 and 11 are driving point respectively 直线1的起始点和终止点 Driving point and receiving point of line 1 直线2的起始点和终止点Driving point and receiving point of line 2 11~24 11~25 11~26 11~27 11~28 1~15 (2.7，12.6) (1.4，13.6) (0，14.5) (-1.6，15.9) (-3.6，17.2) 1~16 (3.2，14.9) (1.6，15.8) (0，16.8) (-1.9，17.9) (-4.0，19.2) 1~17 (3.6，17.0) (1.8，17.9) (0，18.7) (-2.1，19.7) (-4.4，20.7) 1~18 (4.1，19.2) (2.0，19.9) (0，20.5) (-2.3，21.1) (-4.7，22.1) 1~19 (4.5，21.2) (2.2，21.8) (0，22.2) (-2.4，22.8) (-4.9，23.3)

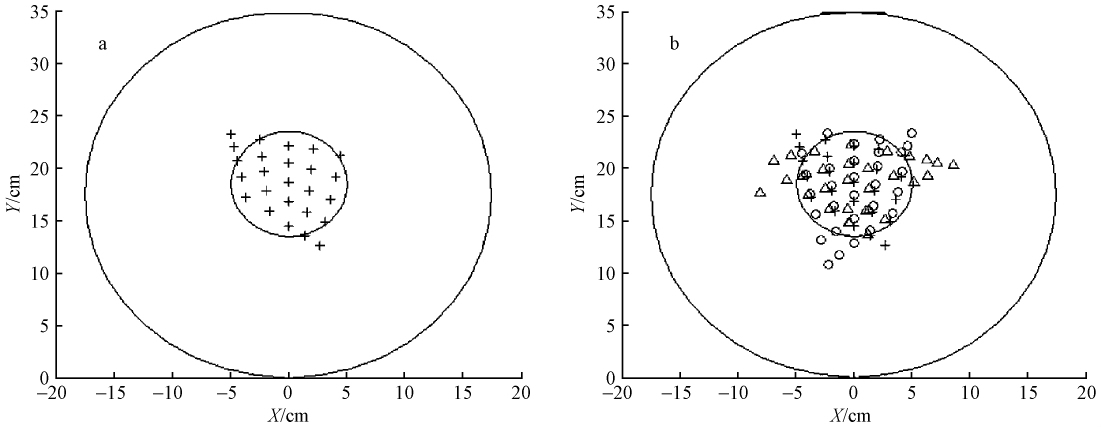
为判定样本横截面内缺陷位置，提出一种判别方法，即在上述二维平面坐标系内，假设2条直线相交于点A(x，y)，并且经SVM分类预测2条直线都经过缺陷，那么判定点A(x，y)处存在缺陷； 反之，不存在缺陷。根据上述方法，利用Matlab软件，模拟原木横截面几何形状，在模拟的二维平面内绘制缺陷点。图 3为绘制的含孔洞(d=10 cm)的横截面二维图。图 3中，大圆代表横截面边缘，小圆代表孔洞边缘，“+”为表 1中坐标点位置。由图 3a可知，此法预测结果未完全覆盖缺陷区域，且在缺陷外围存在错判点，这表明该方法存在不足。 依据该法，若2条直线均被判为通过孔洞缺陷，则判定其交点处有缺陷，而有些情况下这与实际情况不符。例如，当一条直线在交点前经过缺陷，另一条直线在交点后经过缺陷，则该法预测结果将产生偏差。为更准确地辨别孔洞的位置和形状，需改进上述方法。本文根据多点发射的射线交点预测情况进行综合判定。

	图3 利用Matlab构建的原木横截面孔洞缺陷(d=10 cm)位置的描点图 (a.点1和点11为发射点； b.点1，11和点21为发射点) Fig.3 The plotted points simulation of a defective cross section(d=10 cm)diameter when point 1 and 11 are driving points(a) and when point 1，11 and 21 are driving points(b)

仍用含孔洞(d=10 cm)样本横截面为例，分别以样本圆周上的3个等分点作为发射点，将所有经过孔洞的射线交点都绘制在平面图中，如图 3b。其中，采用3种符号分别标记不同发射点所发出的射线交点： 从点1和点11发出的射线交点标记为“+”，从点1和点21发出的标记为“△”，从点11和点21发出的标记为“○”。由图 3b可知，与实际缺陷相比，综合预测的缺陷区域吻合较好，但仍有错判点。

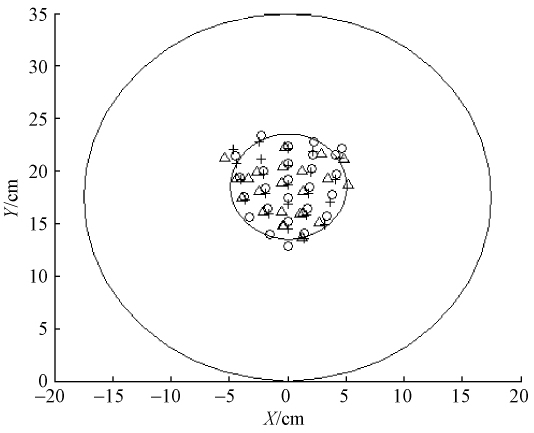
为使模拟图更逼近实际孔洞，需剔除错判点。错判点剔除方法是： 若某一点与其周围距离最近的点均采用相同符号表示，那么将此点剔除。图 4显示的是剔除错判点后的含孔洞样本横截面(d=10 cm)的二维平面描点图。由图 4可知，预测结果与缺陷实际大小、位置及形状符合很好，对缺陷判断较准确。

	图4 除错判点后的原木横截面孔洞缺陷(d=10 cm)的位置描点 Fig.4 The plotted points simulation of a defective cross section (d=10 cm)when erroneous judgment points were removed

为直观显示原木横截面内缺陷位置、大小和形状，构建二维超声断面图像。首先，利用Matlab软件绘制出反映样本横截面的二维平面坐标系；其次，对坐标系内的点赋值，由于健康木材中超声波速度均为810 m·s^-1，因此先将横截面上所有点赋值810；再次，在二维平面内，根据前述方法，找到缺陷点位置，对缺陷点位置处的数值重新赋值，数值为过该点的2个超声波速度中的较大值。

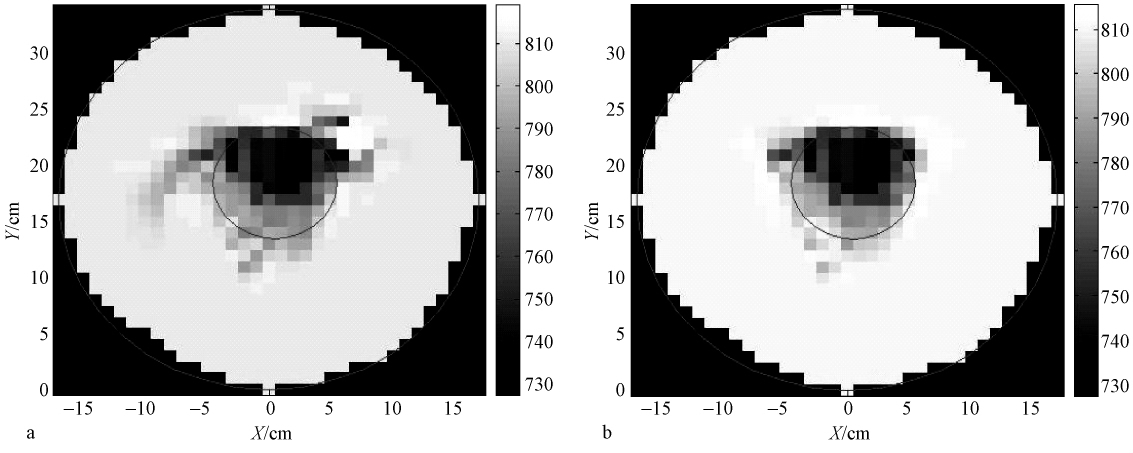
完成横截面内所有点赋值后，需对二维图像填充颜色，实现图像可视化。利用Matlab软件，首先对数据插值处理，然后用bone色图实现颜色填充。图 5a和图 5b分别是含孔洞样本(d=10 cm)横截面存在错判点和剔除错判点后的模拟图。在图 5中，判定有缺陷的位置颜色为深色，健康位置则为白色。与实物图(图 6)比，剔除错判点后的模拟图重合度高，模拟效果理想。

	图5 原木横截面孔洞(d=10 cm)二维超声模拟图像(a.存在错判点;b.剔除错判点) Fig.5 The simulated 2D graph of log sample with a 10 cm hole which includes some erroneous judgment points(a) and doesn’t include the erroneous judgment points(b)

	图6 原木试样实物照片 Fig.6 The actual photo of log sample

1)采用支持向量机可对原木横截面孔洞缺陷大小进行辨识，准确率较高，达到84.78%。

2)提出一种定量判别原木横截面内缺陷点位置的方法，即在建立的二维平面坐标系内，假设2条直线相交于点A(x，y)，如果经过支持向量机分类预测2条直线都过缺陷，那么判定点A(x，y)处存在缺陷； 反之，不存在缺陷。分析了该方法存在的不足，并进行了改进。

3)利用Matlab，实现了基于支持向量机的原木横截面孔洞缺陷二维超声成像。