木材是一种天然的具有层次性、多孔性以及各向异性的生物高分子材料， 对木材断裂表面进行定量分析具有一定难度。通过对木材断裂表面形貌的分析，利用木材断裂表面具有分形几何的特征，引入分形理论为研究木材断裂问题提供了新的方法。

分形的概念是法国数学家Mandelbrot(1982)通过对自然界中不规则几何图形的观察、分析之后提出来的。分形理论是揭示非线性系统中有序和无序、确定和随机的统一问题，于20世纪70年代提出，经过近40年的发展，目前已广泛应用于自然科学和社会科学的各个领域，成为当今国际上很多学科前沿的研究课题之一(董远等，1997； 费本华，1999)。分形体最大的特点和共性就是具有自相似性，这种自相似性是指分形体的任何局部经放大后与整体相似的一种性质，可能是精确的相似、近似的相似、统计意义上的相似。木材断口的形貌特征具有近似的自相似性(费本华等，2003)。

分形理论在金属、陶瓷等线性材料中应用较为广泛。木材是生物材料，许多性能呈现非线性状态，研究其规律较为困难。在木材科学中，如像金属那样用分形维数表述木材的材性等指标，会对木材科学的研究工作产生全新的认识。分形理论在木材科学方面的应用始于20世纪90年代，开始主要是研究木材表面纹理、颜色变异等(Hatzikiriakos et al., 1994； Redinz et al., 1997； Fan et al., 1999； Liu et al., 2002);随着分形理论在木材科学中的应用与推广，科技工作者开始将分形理论应用于木材断裂的研究中。目前，已开展的工作主要是计算木材断口的分形维数，将木材的物理力学性能与木材断口的分形维数做相关性分析。罗蓓等(2010)研究指出分形特征体现在木材力学行为、木材无损检测、木材环境学等诸方面。分形维数是描述分形特征的定量参数，其大小可作为断裂表面的结构状况、材料的性能等的度量，研究(费本华等，2003； 韩天香，2005； Ko Dnas et al., 2009； 季坤等，2009； 张先林等，2009； 许威，2012)表明，木材的断裂韧性、抗弯强度、冲击韧性等与木材断口的分形维数基本呈线性正相关关系。从目前的研究可以看出： 分形维数在木材科学研究领域的应用还有许多不足、盲点； 在分形维数的准确测量上还有待于科研人员去探讨； 有时用分形维数与传统力学性能参数之间尚有不适应。但分形的概念是一个能用来描述断裂、非线性现象的极好工具，方便、快捷、准确地计算木材断口的分形维数，将为分形理论在木材断裂研究中的应用奠定坚实基础。

目前，测量木材断口分形维数的方法有小岛法、数盒子法和垂直截面法等，而最为常用的是小岛法(许威等，2011)。使用小岛法测量断口分形维数时，只有当码尺等于或小于裂纹扩展的最小步长时，得到的结果才是断口的真正分维值； 且小岛法需要破坏原始断面，这给随后的测量、复查等带来一定困难(Lung et al., 1988； Shi et al., 1997； 吉晓华等，2001)。小岛法存在的问题也是大多数测量方法所共有的问题。

本文采用一种新的无损测量方法，用三维光学扫描仪对木材试件断口进行扫描，提取出木材断口的三维片体模型，利用UG NX软件分析木材断口的分形特征，计算木材断口的分形维数。通过对比分析不同树种木材断口分形特征的差别，来揭示不同树种木材断口形态之间的关系。本文为木材断口分形特征的研究提供了一种无损、不受码尺限制、可重复操作的新方法，为分形理论在木材断裂研究方面开辟了新的途径。

试材为产自黑龙江的杉松(Abies holophylla)、银白杨(Populus alba)，参照国标GB/T 1929—2009，GB/T 1937—2009规定的方法，从杉松、 银白杨试材中截取L×T×R=25 mm×10 mm ×25 mm的试件各15个进行横向(即弦向)剪切试验。

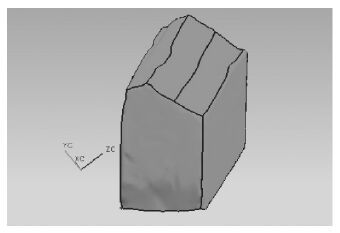
本试验采用德国博尔科曼(Breuckmann)白光三维扫描仪(图 1)对试件的断口进行扫描，提取试件断口的三维片体模型。Breuckmann白光三维扫描仪采用立体相机测量技术和先进的电外差相位测量光栅，可在1 s内获得多达600万的高精度点云数据，测量精度可达4 μm，重复测量精度高，一致性好，可以完整、精确地提取出木材断口的三维片体模型。从经过剪切试验的试件中挑出断裂面凸起的半块试件，用三维扫描仪对其断口进行扫描，提取出试件断口的三维片体模型。图 2为杉松试件断口的三维片体模型。

	图1 Breuckmann白光三维扫描仪 Fig.1 Breuckmann white light 3D scanner

	图2 杉松试件断口三维片体模型 Fig.2 3D block model of Abies holophylla specimen fracture

本试验利用UG NX软件来测量试件断口横截面的面积。

1)将扫描得到的试件断口三维片体模型导入到UG NX软件中。为了方便观察，对导入到UG NX软件中的三维片体模型的断口表面沿断口平面的法线方向进行拉伸，得到试件断口的实体模型。图 3为杉松试件断口的实体模型。

	图3 杉松试件断口实体模型 Fig.3 Entity model of Abies holophylla specimen fracture

2)建立一个与试件断口平面平行的剪切工作截面，步进1 μm，沿着试件断口平面的法线方向移动剪切工作截面，使剪切工作截面与试件断口表面的最高点相切，记录此时剪切工作截面的位置，将该位置记为零点位置，并设指向试件的法向方向为正方向。

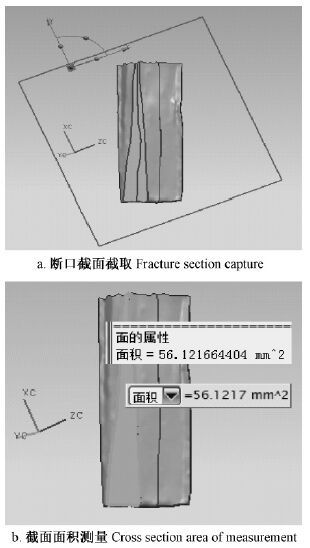
3)沿着正方向移动剪切工作截面，对试件断口实体模型进行切割，每次移动的距离为400 μm，直至剪切工作截面移动到试件断口表面最低点为止，并记录每次剪切工作截面切割断口实体模型的截面面积。由于剪切工作截面切割断口实体模型只是为了便于观察截面的形态变化，隐去了剪切工作截面零点位置一侧的断口实体模型而不是真正地将断口实体模型进行切割，所以无法直接测量截面的面积。但可以提取截面的轮廓线，对轮廓线做一个拉伸使得到的实体平面与截面面积相等，测量这个实体平面的面积即可得到截面面积，面积测量精度为0.001 μm²。图 4为杉松试件断口实体模型截面截取示意图。

	图4 杉松试件断口实体模型截面截取示意 Fig.4 Fracture section capture schematic of Abies holophylla specimen entity model

在双对数坐标系中，建立剪切工作截面距离零点的距离L与其切割断口实体模型得到的横截面面积S的线性关系。以剪切工作截面距离零点的距离L的对数lnL为横坐标，其切割断口实体模型横截面面积S的对数lnS为纵坐标，利用Microsoft Excel软件的散点图对其进行线性拟合，得到lnL和lnS的线性关系式(费本华等，2006)为：

观察试件断口及其实体模型截面形状可以发现，试件断口表面沿垂直于纹理方向凹凸不平高度波动较大，但沿着顺纹理方向断口表面却较为光滑，平整高度波动小； 试件断口截面形状极不规则，并且具有一定的相似性。图 5所示为杉松试件的截面变化图，第一个截面距零点位置350 μm，最后一个截面距零点位置3 950 μm，相邻截面之间的距离为400 μm。从图中可以看出杉松试件的断口截面形状具有相似性，并且前6个截面具有非常明显的相似性，而后4个截面由于接近断口底部而趋于试件的截面形状。

	图5 杉松试件断口截面变化 Fig.5 Cross section variation of Abies holophylla specimen fracture

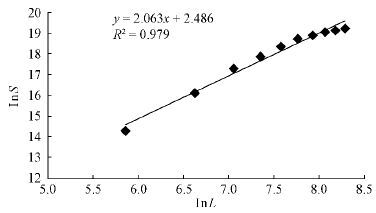
图 6是图 5中各截面的lnL-lnS线性拟合图。从图中可以看出，杉松试件断口在图 5中具有明显相似性的前6个截面在图 6中所对应的点具有非常明显的线性关系，而杉松试件断口各截面的lnL和lnS的线性关系也很显著，具有明显的分形特征，分形维数为2.063。

	图6 lnL-lnS线性拟合 Fig.6 lnL-lnS linear fitting figure

从表 1可以看出，杉松和银白杨剪切断口的lnL-lnS线性回归的拟合优度都大于0.900，在0.955上下浮动，最大值为0.986，最小值为0.918，这说明木材剪切断口的截面面积与截面相应位置对数之间存在着明显的线性关系lnS=D_LlnL+C，木材剪切断口具有明显的分形几何特征。所有杉松和银白杨剪切断口的分形维数D_L均大于面的拓扑维数2而小于体的拓扑维数3。对于试件断口而言，断口分形维数越接近于2，说明试件断口的表面结构简单； 断口分形维数越接近于3，说明断口表面的表面结构较复杂。杉松和银白杨试件断口维数的均值分别为2.050和2.091，表明剪切断口的表面结构较简单，相对平整，这与剪切试件断口的形貌特征一致。二者断口的分形维数存在差异，反映了其显微构造不同：杉松细胞组织结构简单，主要是管胞，排列整齐，材质均匀，因此分形维数相对较小；银白杨细胞组织结构复杂，排列不整齐，分形维数相对较大。

表1 杉松与银白杨试件剪切断口分形维数 Tab.1 Shear fracture fractal dimension of Abies holophylla and Popalus alba specimens

表 1杉松与银白杨试件剪切断口分形维数 Tab.1Shear fracture fractal dimension of Abies holophylla and Popalus alba specimens 编号 No. 杉松Abies holophylla 银白杨Populus alba 维数Dimension 拟合优度Goodness of fit 维数Dimension 拟合优度Goodness of fit 1 2.028 0.953 2.042 0.973 2 2.039 0.965 2.095 0.986 3 2.035 0.918 2.081 0.968 4 2.042 0.948 2.093 0.941 5 2.068 0.964 2.089 0.972 6 2.052 0.973 2.067 0.959 7 2.019 0.933 2.108 0.935 8 2.048 0.946 2.076 0.945 9 2.063 0.979 2.083 0.964 10 2.056 0.965 2.126 0.961 11 2.049 0.935 2.091 0.953 12 2.066 0.958 2.116 0.922 13 2.053 0.942 2.096 0.946 14 2.081 0.961 2.106 0.953 15 2.051 0.936 2.094 0.961

同时，研究还发现杉松和银白杨试件的断口随着剪切工作截面从零点位置(即断口表面的最高点)向断口底部移动，其各剪切工作截面断口部分的分形维数逐渐减小，且与剪切工作截面到零点位置的距离呈线性负相关关系(图 7)。

	图7 杉松试件断口不同剪切工作截面位置处的分形维数关系 Fig.7 Fractal dimension at different position datum of Abies holophylla specimen fracture

不同树种由于微观结构不同，导致其断裂性质也不相同。对杉松和银白杨试件断口的分形维数进行方差分析(表 2)，结果表明： 杉松和银白杨试件断口分形维数之间存在具有统计意义的显著性差异(P=1.38×10^-6<0.01)。因此，断口分形维数可以一种定量化的方式描述木材断口的形态特征及复杂程度。

表2 杉松与银白杨试件断口分形维数方差分析 Tab.2 Fractal dimension analysis of variance of Abies holophylla and Populus alba specimen fracture

表 2杉松与银白杨试件断口分形维数方差分析 Tab.2Fractal dimension analysis of variance of Abies holophylla and Populus alba specimen fracture 差异源Source 离差平方和SS 自由度df 均方差MS F P 组间Columns 0.012 52 1 0.012 52 37.279 73 1.38E-6 组内Within 0.009 40 28 0.000 33 总和Total 0.021 93 29

1)杉松和银白杨试件木材断口截面面积与截面相应位置的对数之间具有明显的线性关系，这种线性关系与截面形状的相似程度呈正相关关系。

2)杉松和银白杨木材断口的分形维数均值分别为2.050和2.091，它越接近于2表明断口表面的表面结构简单，相对平整，越接近3表明断口表面的表面结构复杂。

3)杉松和银白杨木材的断口随着剪切工作截面从零点位置(即断口表面的最高点)向断口底部移动，其各剪切工作截面断口部分的分形维数逐渐减小，且与剪切工作截面到零点位置的距离呈线性负相关关系。

4)杉松和银白杨木材断口分形维数之间存在具有统计意义的显著性差异。