文章信息
- 符利勇, 雷渊才, 曾伟生
- Fu Liyong, Lei Yuancai, Zeng Weisheng
- 几种相容性生物量模型及估计方法的比较
- Comparison of Several Compatible Biomass Models and Estimation Approaches
- 林业科学, 2014, 50(6): 42-54
- Scientia Silvae Sinicae, 2014, 50(6): 42-54.
- DOI: 10.11707/j.1001-7488.20140606
-
文章历史
- 收稿日期:2013-06-19
- 修回日期:2013-08-29
-
作者相关文章
2. 国家林业局调查规划设计院 北京 100714
2. Academy of Forest Inventory and Planning, State Forestry Administration Beijing 100714
森林生态系统作为陆地生态系统的主体,在维护全球气候系统、调节全球碳平衡、减缓大气温室气体浓度上升等方面具有不可替代的作用,世界各国越来越重视对其生物量的估计、监测和评价。生物量建模是其中的一项核心内容,国内外关于它的研究非常多(Parresol,2001; Zhang et al.,2004; Bi et al.,2004; Fehrmann et al.,2008; Zeng et al.,2011; 2012; Fu et al.,2012; 曾伟生等,2010a; 2010b; 符利勇等,2011a; 李海奎等,2012),主要建模方法可归纳为传统回归方法(Jenkins et al.,2003; Vallet et al.,2006; Basuki et al.,2009)、非线性似然无关回归方法(Parresol,2001; Bi et al.,2004)、线性或非线性联合估计方法(骆期邦等,1999; 唐守正等,2000)、哑变量方法(Zeng et al.,2011; Fu et al.,2012)、混合模型方法(Zhang et al.,2004; Fehrmann et al.,2008; Fu et al.,2012; 曾伟生等,2010a; 符利勇等,2011a; 2011b)和度量误差模型方法(曾伟生等,2010b; 李海奎等; 2012; Zeng et al.,2012)等。
尽管作为大尺度森林生物量监测,更多关注的是总生物量及地上和地下生物量,但是在研究生态系统生产力、能量和营养物质分布时,需把总生物量分解成不同的组成部分(Waring et al.,1998),例如把地上生物量分解成树干和树冠,树干进一步分解成干材和干皮,树冠进一步分解成树枝和树叶等。除此之外,在进行生态系统分析时,总物质必须满足分解和合成相一致(分量加起来等于总量)。因此,构建地上各分量单木生物量相容性模型一直为世界生态学家和林学家所重视。到目前为止,已提出了不同方法,最常见的有非线性似然无关回归方法(Parresol,2001; Bi et al.,2004)、比例平差法(唐守正等,2000)和线性或非线性联合估计方法(骆期邦等,1999; 唐守正等,2000)等。非线性似然无关回归法最先由Parresol(2001)提出,是根据非线性似然无关理论保证了干材、干皮和树冠生物量的可加性,同时单木生物量各分量之间相互关系可通过误差项方差协方差矩阵来描述。比例平差法是解决单木生物量相容性问题最简单且最直接的方法,是基于各分量占总量的比例之和等于1提出的(唐守正等,2000),各分量模型中参数通过最小二乘法独立求解得到,基于比例平差是在不考虑单木生物量相容性的情况下给出的最优估计。唐守正等(2000)提出了线性或非线性联合估计方法,该方法将各分量进行联合建模,联立求解。然而,对这些方法的详细比较研究至今尚未报道,主要原因可能是这些方法的数学处理比较复杂和大量单木生物量数据获取比较困难;同时由于缺乏全面的比较研究,人们建立相容性生物量模型时无法合理选择有效方法。为此,本研究在考虑林分起源和不考虑林分起源2种情形下,以南方150株马尾松(Pinus massoniana)地上生物量数据为例,对传统独立模型方法、比例平差法、非线性似然无关回归方法以及非线性联立方程组法进行系统比较,分析各自特点,这对森林生物量建模和监测有着重要意义。
1 数据本文所用数据为我国南方马尾松的立木地上生物量实测数据,共150 株样木,采集时间为2009 年6—9 月,采集地点涉及江苏、浙江、安徽、福建、江西、湖南、广东、广西、贵州9省区。其中随机抽取120 株样本作为建模数据,另外30 株样本作为检验数据。建模数据中样本单元数的选取大体上按各省资源多少分配,并兼顾天然和人工起源,其中,天然62 株,人工58 株; 样木数按2,4,6,8,12,16,20,26,32,38 cm 以上共10 个径阶均匀分配(除26,32 cm 径阶分别为14,16 株外,其他径阶均为15 株),每个径阶的样木数按树高级从低到高也尽量均匀分配,在大尺度范围内具有广泛的代表性。全部样木都实测胸径、地径和冠幅,将样木伐倒后,测量树干长度(树高)和活树冠长度(冠长),分干材、干皮、树枝、树叶称鲜质量,并分别抽取样品带回实验室,在85 ℃恒温下烘干至恒重,根据样品鲜质量和干质量分别推算出样木各部分干质量并汇总得到地上部分干质量。建模数据(120株)和检验数据(30株)统计信息见表 1。具体的数据调查和测定方法见文献符利勇等(2011c)。
|
|
选用常用异速方程形式Y=β0X1β1···Xpβp+ε构建地上单木总生物量和各分量生物量模型(基础模型)。考虑自变量个数把模型分为一元、二元和多元模型,并分别建立模型。然后,基于建立的基础模型,分别使用传统独立模型法、比例平差法、非线性似然无关回归方法和非线性联立方程组法建立地上单木总生物量和各分量生物量系统方程并进行估计,根据估计结果对各方法进行比较。
2.1 单木生物量模型 2.1.1 自变量确定设fi(x)(i=1,…,7)分别表示地上总生物量以及树干、干材、树皮、树冠、树枝和树叶各分量生物量方程。根据方程fi(x)(i=1,…,7)所包含的单木变量(自变量)个数把生物量模型分为一元、二元和多元生物模型。
1)一元回归模型 本文选用常见的CAR(constant allometric ratio)形式fi(x)=αxb(Kittredge,1994)构建各分量一元生物量模型。候选自变量分别为胸径(D)、地径(D0)、树高(H)、年龄(A)、冠幅(CW)和枝下高(CH)。
2)二元回归模型 按照CAR函数形式fi(x)=αx1bx2c,对自变量D,D0,H,A,CW和CH共15种两两组合进行比较,最终确定2个与生物量相关性最强的林分变量构建生物量模型。
3)多元回归模型 按照CAR函数形式fi(x)=αx1bx2cx3d,通过对自变量D,D0,H,A,CW和CH共20种组合进行比较,确定最终各分量的三元生物量模型。
所选评价指标有平均残差( $ \bar e$ )、残差方差(ξ)、均方误差(δ)和决定系数(R2),计算公式如下:
| $ \bar e = \sum {\left( {{y_i} - {{\hat y}_i}} \right)/N,} $ | (1) |
| $ \xi = \sum {{{\left( {{y_i} - {{\hat y}_i}} \right)}^2}/\left( {N - 1} \right),} $ | (2) |
| $ \delta = \sqrt {{{\bar e}^2} + \xi } 。 $ | (3) |
式中: yi和 ${\hat y_i} $ 分别为生物量的真实值和预测值;N为总观测数。
2.1.2 考虑起源对生物量的影响为分析不同林分起源(天然林和人工林)中马尾松各分量生物量差异,引入哑变量S,当S=0时为人工林,S=1时为天然林。各分量生物量模型为:
| $ {W_i} = {f_i}\left( {x,S} \right) + {\varepsilon _i},\left( {i = 1, \cdots ,7} \right)。 $ | (4) |
式中: εi为误差项。
2.1.3 异方差生物量模型中普遍存在异方差,因此不满足普通最小二乘法要求等方差的假设条件。为消除异方差,常用方法有对数回归法和加权回归法(Tang et al.,2000; Zeng et al.,2010)。本文采用加权最小二乘法求解,权函数[模型(5)]通过各分量独立拟合方程的方差确定,所选用的候选模型形式有指数函数、对数函数、幂函数、Logistic函数以及原基础模型本身,利用评价指标AIC(akaike information criterion)确定最终权函数:
| $ {\varphi _i} = 1/g{\left( x \right)^2}。 $ | (5) |
利用各分量独立的生物量模型求解,该方法不能保证各分量生物量(干材、干皮、树枝和树叶或者树干和树冠)之和等于总生物量:
| $ {W_i} = {f_i}\left( x \right) + {\varepsilon _i},\left( {i = 1, \cdots ,7} \right)。 $ | (6) |
式中: fi(x)为各分量独立回归模型; W1~W7分别表示地上总生物量以及树干、干材、树皮、树冠、树枝和树叶各分量生物量。
2.3 非线性比例平差法从相容性的定义出发,要满足各分量之和等于总量,实际上就是满足各分量占总量的比例之和等于1,唐守正等(2000)以此为基础提出了比例平差法。根据各分量分配层次的不同,可得到总量直接控制方案(Procedure Ⅰ)和分级联合控制方案(Procedure Ⅱ)。
2.3.1 总量直接控制平差法由总量直接平差分配给干材、树皮、枝和叶,从而保证各分量之和等于总量。具体各分量的模型表达式如下:
| $ {W_3} = \frac{{{f_3}\left( x \right)}}{{{f_3}\left( x \right) + {f_4}\left( x \right) + {f_6}\left( x \right) + {f_7}\left( x \right)}} + {W_1} + {\varepsilon _3}; $ | (7) |
| $ {W_4} = \frac{{{f_4}\left( x \right)}}{{{f_3}\left( x \right) + {f_4}\left( x \right) + {f_6}\left( x \right) + {f_7}\left( x \right)}} + {W_1} + {\varepsilon _4}; $ | (8) |
| $ {W_6} = \frac{{{f_6}\left( x \right)}}{{{f_3}\left( x \right) + {f_4}\left( x \right) + {f_6}\left( x \right) + {f_7}\left( x \right)}} + {W_1} + {\varepsilon _6}; $ | (9) |
| $ {W_7} = \frac{{{f_7}\left( x \right)}}{{{f_3}\left( x \right) + {f_4}\left( x \right) + {f_6}\left( x \right) + {f_7}\left( x \right)}} + {W_1} + {\varepsilon _7}; $ | (10) |
| $ {W_1} = {f_1}\left( x \right) + {\varepsilon _1}。 $ | (11) |
式中: W1,W3,W4,W6和W7分别表示地上总生物量、干材、干皮、树枝和树叶生物量的估计值(下面类同);f1(x),f3(x),f4(x),f6(x)和f7(x)分别为地上总生物量以及各分量干材、干皮、树枝和树叶生物量的基础模型(下面类同)。参数由传统最小二乘法计算得到。
2.3.2 分级联合控制平差法分级联合控制平差法,即首先把地上总生物量分配给树干和树冠,然后再把树干生物量分配给干材和干皮,树冠生物量分配给树枝和树叶。该方法不但实现了干材、干皮、树枝和树叶之和等于总量,而且还实现了树干和树冠之和等于总量(唐守正,2000)。具体各分量的模型表达式如下:
| $ {W_3} = \frac{{{f_3}\left( x \right)}}{{{f_3}\left( x \right) + {f_4}\left( x \right)}}\frac{{{f_2}\left( x \right)}}{{{f_2}\left( x \right) + {f_5}\left( x \right)}}{W_1} + {\varepsilon _3}; $ | (12) |
| $ {W_4} = \frac{{{f_4}\left( x \right)}}{{{f_3}\left( x \right) + {f_4}\left( x \right)}}\frac{{{f_2}\left( x \right)}}{{{f_2}\left( x \right) + {f_5}\left( x \right)}}{W_1} + {\varepsilon _4}; $ | (13) |
| $ {W_6} = \frac{{{f_6}\left( x \right)}}{{{f_6}\left( x \right) + {f_7}\left( x \right)}}\frac{{{f_5}\left( x \right)}}{{{f_2}\left( x \right) + {f_5}\left( x \right)}}{W_1} + {\varepsilon _6}; $ | (14) |
| $ {W_7} = \frac{{{f_7}\left( x \right)}}{{{f_6}\left( x \right) + {f_7}\left( x \right)}}\frac{{{f_5}\left( x \right)}}{{{f_2}\left( x \right) + {f_5}\left( x \right)}}{W_1} + {\varepsilon _7}; $ | (15) |
| $ {W_1} = {f_1}\left( x \right) + {\varepsilon _1}。 $ | (16) |
式中: f2(x)和f5(x)分别为树干和树冠生物量的基础模型(下面类同),参数由传统最小二乘法计算得到。
2.4 非线性似然无关回归方法非线性似然无关回归方法(nonlinear seemingly unrelated regressions)由Parresol(2001)提出,该方法不仅保证了各分量生物量方程的可加性(即生物量相容),同时还考虑了各分量之间的相关性,因此被广泛应用。模型表达式如下:
| $ \left\{ \begin{array}{l} {W_3} = {f_3}\left( x \right) + {\varepsilon _3};\\ {W_4} = {f_4}\left( x \right) + {\varepsilon _4};\\ {W_6} = {f_6}\left( x \right) + {\varepsilon _6};\\ {W_7} = {f_7}\left( x \right) + {\varepsilon _7};\\ {W_1} = {f_1}\left( x \right) = {f_3}\left( x \right) + {f_4}\left( x \right) + {f_6}\left( x \right) + {f_7}\left( x \right) + {\varepsilon _1}。 \end{array} \right. $ | (17) |
式中: f1(x),f3(x),f4(x),f6(x)和f7(x)分别为地上总生物量以及各分量干材、干皮、树枝和树叶生物量的基础模型,模型参数是由非线性似然无关回归方法估计得到,该方法的详细介绍见Parresol(2001)。
2.5 非线性联立方程组法非线性联立方程组是近代统计分析方法之一,研究当模型的应变量是另外模型的自变量或模型之间有共同参数等参数估计问题。与非线性似然无关回归方法一样,该方法不仅保证各分量生物量相容,同时还可分析各分量之间的相关性。同样,非线性联立方程组也考虑总量直接控制和分级联合控制2种方案。非线性联立方程组的详细介绍见唐守正等(2008)。
2.5.1 总量控制联立方程组与总量控制比例平差法相似,唯一不同的是,该方法对各分量进行联合建模,模型中参数通过联立方程组法求解得到。模型表达式如下:
| $ \left\{ \begin{array}{l} {W_3} = \frac{{{f_3}\left( x \right)}}{{{f_3}\left( x \right) + {f_4}\left( x \right) + {f_6}\left( x \right) + {f_7}\left( x \right)}}{{\hat W}_1} + {\varepsilon _3};\\ {W_4} = \frac{{{f_4}\left( x \right)}}{{{f_3}\left( x \right) + {f_4}\left( x \right) + {f_6}\left( x \right) + {f_7}\left( x \right)}}{{\hat W}_1} + {\varepsilon _4};\\ {W_3} = \frac{{{f_6}\left( x \right)}}{{{f_3}\left( x \right) + {f_4}\left( x \right) + {f_6}\left( x \right) + {f_7}\left( x \right)}}{{\hat W}_1} + {\varepsilon _6};\\ {W_3} = \frac{{{f_7}\left( x \right)}}{{{f_3}\left( x \right) + {f_4}\left( x \right) + {f_6}\left( x \right) + {f_7}\left( x \right)}}{{\hat W}_1} + {\varepsilon _7}。 \end{array} \right. $ | (19) |
式中: ${\hat W_1} $ 由基础模型计算得到, ${\hat W_1} = {f_1}\left(x \right)$ 。
2.5.2 分级联合控制联立方程组该方法与分级联合控制比例平差法相似,唯一不同的是,各分量进行联合建模,模型中参数通过联立方程组法求解得到。模型表达式如下:
| $ \left\{ \begin{array}{l} {W_3} = \frac{{{f_3}\left( x \right)}}{{{f_3}\left( x \right) + {f_4}\left( x \right)}}\frac{{{f_2}\left( x \right)}}{{{f_2}\left( x \right) + {f_5}\left( x \right)}}\hat W + {\varepsilon _3};\\ {W_4} = \frac{{{f_4}\left( x \right)}}{{{f_3}\left( x \right) + {f_4}\left( x \right)}}\frac{{{f_2}\left( x \right)}}{{{f_2}\left( x \right) + {f_5}\left( x \right)}}\hat W + {\varepsilon _4};\\ {W_6} = \frac{{{f_6}\left( x \right)}}{{{f_6}\left( x \right) + {f_7}\left( x \right)}}\frac{{{f_5}\left( x \right)}}{{{f_2}\left( x \right) + {f_5}\left( x \right)}}\hat W + {\varepsilon _6};\\ {W_7} = \frac{{{f_7}\left( x \right)}}{{{f_6}\left( x \right) + {f_7}\left( x \right)}}\frac{{{f_5}\left( x \right)}}{{{f_2}\left( x \right) + {f_5}\left( x \right)}}\hat W + {\varepsilon _7}。 \end{array} \right. $ | (20) |
式中: $\hat W $ 由基础模型计算得到, $ {\hat W_1} = {f_1}\left(x \right)$ 。
2.6 模型评价利用前面所介绍的方法构建一元、二元和多元相容性生物量模型,根据是否包含哑变量S把所有模型分为2种类型,即未考虑林分起源和考虑林分起源的相容性生物量模型。本研究首先通过建模数据利用均方误差(δ)和决定系数(R2)2个指标分别选出考虑和不考虑林分起源时一元、二元和多元对应的最优相容性生物量模型,然后根据检验数据利用平均残差( $ \bar e$ )、残差方差(σ2)、均方误差(δ)和总相对误差(RS)[式(21)]4个指标对各自的一元、二元和多元最优模型进行比较和评价,最终确定考虑起源和不考虑起源时对应的一种相容性生物量模型。非线性似然无关回归方法的计算在SAS 9.2上实现,其他所有计算在ForStat2.2上实现。
| $ RS = \sum {\left( {{y_i} - {{\hat y}_i}} \right)} /\sum {{{\hat y}_i}} \times 100\% 。 $ | (21) |
由变量逐步筛选方法最终确定一元、二元和三元各分量生物量模型中自变量分别为D,D和H,D、H和CW。不考虑林分起源对生物量影响的各分量一元、二元和三元生物量模型的表达式见模型(22),(24)和(26)。考虑林分起源对生物量影响的各分量一元、二元和三元生物量模型的表达式见模型(23),(25)和(27)。通过比较可知,幂函数形式的权函数消除异方差效果最好,各分量一元、二元和三元生物量模型的加权函数见表 2。
|
|
| $ {W_{ij}} = {f_i}\left( {{D_j}} \right) = {a_i}D_j^{{b_i}}; $ | (22) |
| $ {W_{ij}} = {f_i}\left( {{D_j},{S_j}} \right) = \left( {{a_i} + {c_i}{S_j}} \right)D_j^{\left( {{b_i} + {d_i}{S_j}} \right)}; $ | (23) |
| $ {W_{ij}} = {f_i}\left( {{D_j},{H_j}} \right) = {a_i}D_j^{{b_i}}H_j^{{c_j}}; $ | (24) |
| $ {W_{ij}} = {f_i}\left( {{D_j},{H_j},{S_j}} \right) = \left( {{a_j} + {c_j}{S_j}} \right)D_j^{\left( {{b_i} + {S_j}} \right)}H_j^{\left( {{e_i} + {f_i}{S_j}} \right)}; $ | (25) |
| $ {W_{ij}} = {f_i}\left( {{D_j},{H_j},C{W_j}} \right) = {a_i}D_j^{{b_i}}H_j^{{c_i}}CW_j^{{d_i}}; $ | (26) |
| $ \begin{array}{l} {W_{ij}} = {f_i}\left( {{D_j},{H_j},C{W_j},{S_j}} \right) = \\ \;\;\;\;\;\;\;\;\left( {{a_j} + {e_i}{S_j}} \right)D_j^{\left( {{b_i} + {f_i}{S_j}} \right)}H_j^{\left( {{c_i} + {g_i}{S_j}} \right)}CW_j^{\left( {{d_i} + {h_i}{S_j}} \right)} + {\varepsilon _{ij}}。 \end{array} $ | (27) |
式中:i=1,…,7分别代表地上总生物量和树干、干材、干皮、树冠、树枝、树叶生物量;j=1,…,N; ai-hi为第i分项所对应的参数; Dj,Hj,CWj,Sj分别为第j株样木胸高直径、树高、冠幅和林分起源类型; εij为误差项。
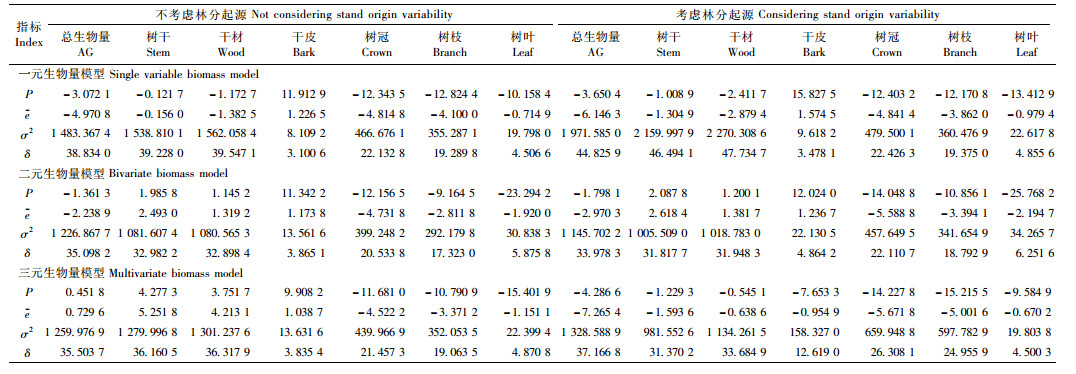
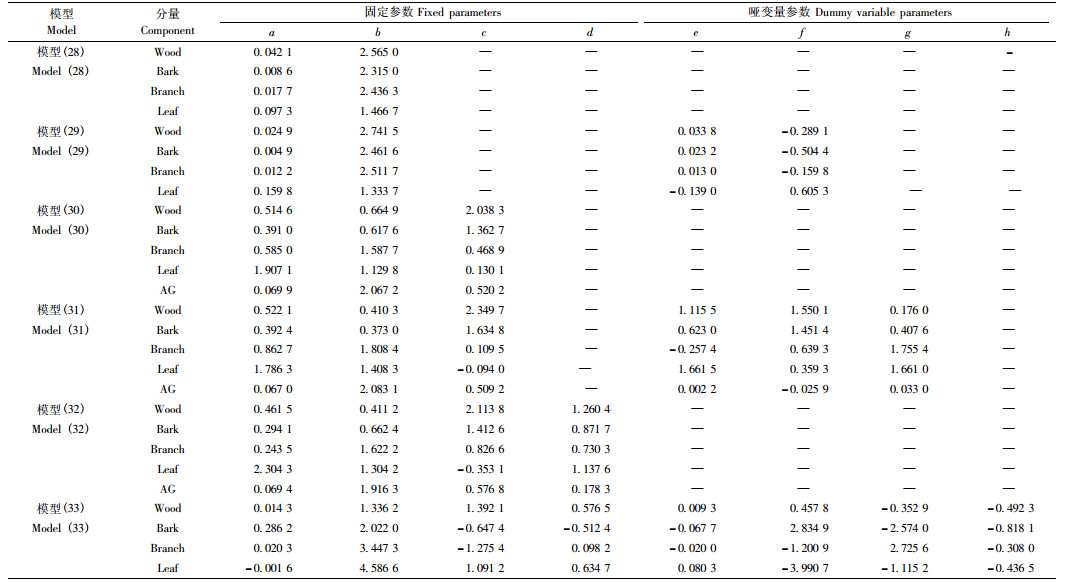
3.2 一元模型附表 1为一元的传统独立模型法、总量直接控制比例平差法、分级联合控制比例平差法、非线性似然无关回归法、总量直接控制联立方程组法以及分级联合控制联立方程组法在考虑或不考虑林分起源情形下对建模数据进行拟合时的评价指标。这些方法中,传统独立模型不能保证各分量之和等于地上总生物量,即不能保证相容性,而其他方法都能保证生物量相容。从表中可看出,各种方法对各分量生物量的拟合效果都较高,拟合精度非常接近。总体而言,在考虑和不考虑林分起源时,非线性似然无关回归法 [分别见模型(28)和(29)]拟合效果都比其他方法稍好,因此选用该方法对生物量模型做进一步分析。模型(28)和(29)各参数估计值见附表 4。
| $ \left\{ \begin{array}{l} {W_{3j}} = {a_3}D_j^{{b_3}} + {\varepsilon _{3j}};\\ {W_{{\rm{4}}j}} = {a_{\rm{4}}}D_j^{{b_{\rm{4}}}} + {\varepsilon _{{\rm{4}}j}};\\ {W_{{\rm{6}}j}} = {a_{\rm{6}}}D_j^{{b_{\rm{6}}}} + {\varepsilon _{{\rm{6}}j}};\\ {W_{{\rm{7}}j}} = {a_{\rm{7}}}D_j^{{b_{\rm{7}}}} + {\varepsilon _{{\rm{7}}j}};\\ {W_{1j}} = {a_3}D_j^{{b_3}} + {a_4}D_j^{{b_4}} + {a_6}D_j^{{b_6}} + {a_7}D_j^{{b_7}} + {\varepsilon _{1j}}。 \end{array} \right. $ | (28) |
| $ \begin{array}{l} \left\{ \begin{array}{l} {W_{3j}} = \left( {{a_3} + {c_3}{S_j}} \right)D_j^{\left( {{b_3} + {d_3}S} \right)} + {\varepsilon _{3j}};\\ {W_{4j}} = \left( {{a_4} + {c_4}{S_j}} \right)D_j^{\left( {{b_4} + {d_4}S} \right)} + {\varepsilon _{4j}};\\ {W_{6j}} = \left( {{a_6} + {c_6}{S_j}} \right)D_j^{\left( {{b_6} + {d_6}S} \right)} + {\varepsilon _{6j}};\\ {W_{7j}} = \left( {{a_7} + {c_7}{S_j}} \right)D_j^{\left( {{b_7} + {d_7}S} \right)} + {\varepsilon _{7j}};\\ {W_{1j}} = \left( {{a_3} + {c_3}{S_j}} \right)D_j^{\left( {{b_3} + {d_3}S} \right)} + \end{array} \right.\\ \;\;\;\;\;\;\;\;\;\;\;\left( {{a_{\rm{4}}} + {c_{\rm{4}}}{S_j}} \right)D_j^{\left( {{b_{\rm{4}}} + {d_{\rm{4}}}S} \right)} + \;\\ \;\;\;\;\;\;\;\;\;\;\left( {{a_{\rm{6}}} + {c_{\rm{6}}}{S_j}} \right)D_j^{\left( {{b_{\rm{6}}} + {d_{\rm{6}}}S} \right)} + \\ \;\;\;\;\;\;\;\;\;\;\left( {{a_{\rm{7}}} + {c_{\rm{7}}}{S_j}} \right)D_j^{\left( {{b_{\rm{7}}} + {d_{\rm{7}}}S} \right)} + {\varepsilon _{1j}}。 \end{array} $ | (29) |
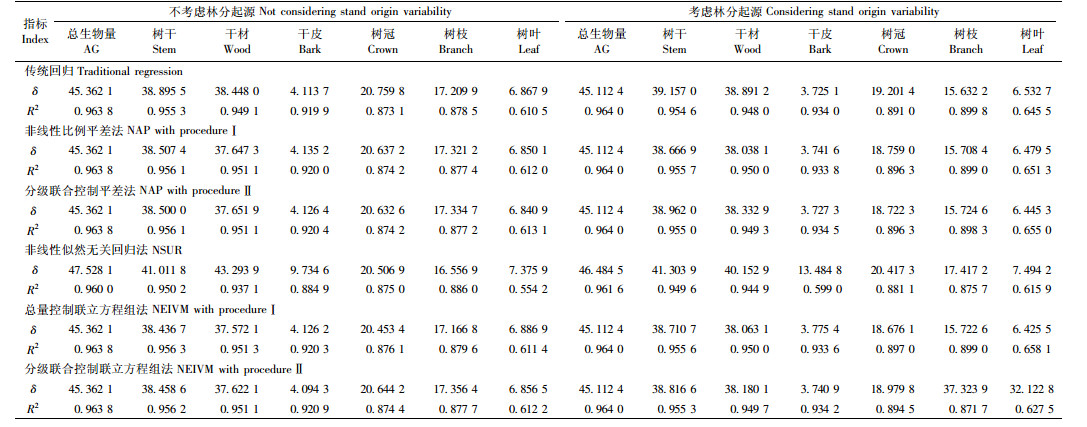
附表 2为各方法对应的二元模型在考虑或不考虑林分起源情形下对建模数据进行拟合时的评价指标。从附表 2中可知,与一元模型计算结果相类似,各方法拟合精度非常接近且拟合效果都较高。总体而言,在考虑或不考虑林分起源时,总量直接控制联立方程组法 [分别见模型(30)和(31)]拟合效果都比其他方法稍好,因此选用该方法对生物量模型做进一步分析。与一元模型相比较,各方法对应的二元模型能进一步提高模型拟合精度。模型(30)和(31)中的参数估计值见附表 4。
| $ \left\{ \begin{array}{l} 干材{W_{3j}} = \frac{{{a_3}D_j^{{b_3}}H_j^{{c_3}}}}{{{W_0}}}{{\hat W}_{1j}} + {\varepsilon _{3j}};\\ 干皮{W_{4j}} = \frac{{{a_4}D_j^{{b_4}}H_j^{{c_4}}}}{{{W_0}}}{{\hat W}_{1j}} + {\varepsilon _{4j}};\\ 树枝{W_{6j}} = \frac{{{a_6}D_j^{{b_6}}H_j^{{c_6}}}}{{{W_0}}}{{\hat W}_{1j}} + {\varepsilon _{6j}};\\ 树叶{W_{7j}} = \frac{{{a_7}D_j^{{b_7}}H_j^{{c_7}}}}{{{W_0}}}{{\hat W}_{7j}} + {\varepsilon _{7j}}。 \end{array} \right. $ | (30) |
式中: $ {\hat W_{1j}}$ 为第j株样木地上总生物量,由传统的独立模型计算得到,计算公式如下:
| $ {{\hat W}_{1j}} = {a_1}D_j^{{b_1}}H_j^{{c_1}} + {\varepsilon _{1j}}。 $ |
W0为干材、干皮、树枝和树叶各分量生物量总和,由以下公式计算得到:
| $ {{\hat W}_0} = {a_3}D_j^{{b_3}}H_j^{{c_3}} + {a_4}D_j^{{b_4}}H_j^{{c_4}} + {a_6}D_j^{{b_6}}H_j^{{c_6}} + {a_7}D_j^{{b_7}}H_j^{{c_7}}。 $ |
| $ \left\{ \begin{array}{l} 干材{W_{3j}} = \frac{{\left( {{a_3} + {c_3}{S_j}} \right)D_j^{\left( {{b_3} + {d_3}{S_j}} \right)}H_j^{\left( {{e_3} + {f_3}{S_j}} \right)}}}{{{W_0}}}{{\hat W}_{1j}} + {\varepsilon _{3j}};\\ 干皮{W_{4j}} = \frac{{\left( {{a_4} + {c_4}{S_j}} \right)D_j^{\left( {{b_4} + {d_4}{S_j}} \right)}H_j^{\left( {{e_4} + {f_4}{S_j}} \right)}}}{{{W_0}}}{{\hat W}_{1j}} + {\varepsilon _{4j}};\\ 树枝{W_{6j}} = \frac{{\left( {{a_6} + {c_6}{S_j}} \right)D_j^{\left( {{b_6} + {d_6}{S_j}} \right)}H_j^{\left( {{e_6} + {f_6}{S_j}} \right)}}}{{{W_0}}}{{\hat W}_{1j}} + {\varepsilon _{6j}};\\ 树叶{W_{7j}} = \frac{{\left( {{a_7} + {c_7}{S_j}} \right)D_j^{\left( {{b_7} + {d_7}{S_j}} \right)}H_j^{\left( {{e_7} + {f_7}{S_j}} \right)}}}{{{W_0}}}{{\hat W}_{1j}} + {\varepsilon _{7j}}. \end{array} \right. $ | (31) |
其中, $ {{\hat W}_{1j}}$ 和W0由以下公式计算得到:
| $ \begin{array}{l} {{\hat W}_{1j}} = {f_1}\left( {{D_j},{H_j},{S_j}} \right) = \\ \;\;\;\;\;\;\;\;\left( {{a_1} + {c_1}{S_j}} \right)D_j^{\left( {{b_1} + {d_1}{S_j}} \right)}H_j^{\left( {{e_1} + {f_1}{S_j}} \right)} + {\varepsilon _{1j}};\\ {W_0} = \left( {{a_3} + {c_3}{S_j}} \right)D_j^{\left( {{b_3} + {d_3}{S_j}} \right)}H_j^{\left( {{e_3} + {f_3}{S_j}} \right)} + \\ \;\;\;\;\;\;\;\left( {{a_4} + {c_4}{S_j}} \right)D_j^{\left( {{b_4} + {d_4}{S_j}} \right)}H_j^{\left( {{e_4} + {f_4}{S_j}} \right)} + \\ \;\;\;\;\;\;\;\left( {{a_6} + {c_6}{S_j}} \right)D_j^{\left( {{b_6} + {d_6}{S_j}} \right)}H_j^{\left( {{e_6} + {f_6}{S_j}} \right)} + \\ \;\;\;\;\;\;\;\left( {{a_7} + {c_7}{S_j}} \right)D_j^{\left( {{b_7} + {d_7}{S_j}} \right)}H_j^{\left( {{e_7} + {f_7}{S_j}} \right)}。 \end{array} $ |
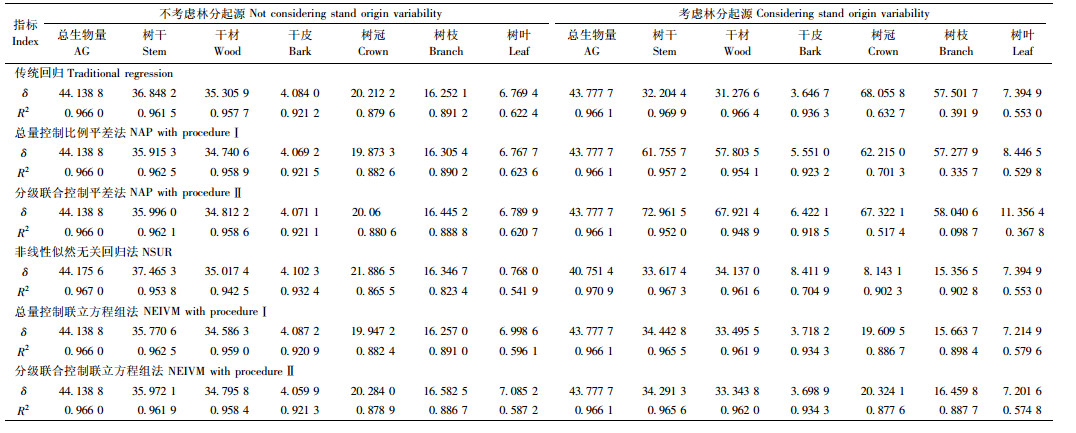
附表 3为各方法对应的三元模型在考虑或不考虑林分起源情形下对建模数据进行拟合时的评价指标。从附表 3中可知,与一元和二元模型类似,所有方法对各分量生物量的拟合效果都较高,拟合精度非常接近。总体而言,当不考虑林分起源时,总量直接控制联立方程组法[模型(32)] 拟合效果比其他方法稍好,当考虑林分起源时,非线性似然无关回归法拟合效果最好[模型(33)]。在二元模型的基础上,当模型考虑冠幅因子时能进一步提高模型拟合精度。模型(32)和(33)中的参数估计值见附表 4。
| $ \left\{ \begin{array}{l} 干材 {W_{3j}} = \frac{{{a_3}D_j^{{b_3}}H_j^{{c_3}}CW_j^{{d_3}}}}{{{W_0}}}{{\hat W}_{1j}} + {\varepsilon _{3j}};\\ 干皮{W_{{\rm{4}}j}} = \frac{{{a_{\rm{4}}}D_j^{{b_{\rm{4}}}}H_j^{{c_{\rm{4}}}}CW_j^{{d_{\rm{4}}}}}}{{{W_0}}}{{\hat W}_{1j}} + {\varepsilon _{{\rm{4}}j}};\\ 树枝{W_{6j}} = \frac{{{a_6}D_j^{{b_6}}H_j^{{c_6}}CW_j^{{d_6}}}}{{{W_0}}}{{\hat W}_{1j}} + {\varepsilon _{6j}};\\ 树叶{W_{7j}} = \frac{{{a_7}D_j^{{b_7}}H_j^{{c_7}}CW_j^{{d_7}}}}{{{W_0}}}{{\hat W}_{1j}} + {\varepsilon _{7j}}。 \end{array} \right. $ | (32) |
其中,
| $ \begin{array}{l} {{\hat W}_{1j}} = {a_1}D_j^{{b_1}}H_j^{{c_1}}CW_j^{{d_1}} + {\varepsilon _{1j}},\\ {W_0} = {a_3}D_j^{{b_3}}H_j^{{c_3}}CW_j^{{d_3}} + {a_{\rm{4}}}D_j^{{b_{\rm{4}}}}H_j^{{c_{\rm{4}}}}CW_j^{{d_{\rm{4}}}} + \\ \;\;\;\;\;\;{a_6}D_j^{{b_6}}H_j^{{c_6}}CW_j^{{d_6}} + {a_7}D_j^{{b_7}}H_j^{{c_7}}CW_j^{{d_7}}.\\ 干材{W_{3j}} = \left( {{a_3} + {e_3}{S_j}} \right)D_j^{\left( {{b_3} + {f_3}{S_j}} \right)}\\ \;\;\;\;\;\;\;\;\;\;\;\;\;H_j^{\left( {{c_3} + {g_3}{S_j}} \right)}CW_j^{\left( {{d_3} + {h_3}{S_j}} \right)} + {\varepsilon _{3j}};\\ 干皮{W_{4j}} = \left( {{a_4} + {e_4}{S_j}} \right)D_j^{\left( {{b_4} + {f_4}{S_j}} \right)}\\ \;\;\;\;\;\;\;\;\;\;\;\;\;H_j^{\left( {{c_4} + {g_4}{S_j}} \right)}CW_j^{\left( {{d_4} + {h_4}{S_j}} \right)} + {\varepsilon _{4j}};\\ 树枝{W_{6j}} = \left( {{a_6} + {e_6}{S_j}} \right)D_j^{\left( {{b_6} + {f_6}{S_j}} \right)}\\ \;\;\;\;\;\;\;\;\;\;\;\;\;H_j^{\left( {{c_6} + {g_6}{S_j}} \right)}CW_j^{\left( {{d_6} + {h_6}{S_j}} \right)} + {\varepsilon _{6j}};\\ 树叶{W_{7j}} = \left( {{a_7} + {e_7}{S_j}} \right)D_j^{\left( {{b_7} + {f_7}{S_j}} \right)}\\ \;\;\;\;\;\;\;\;\;\;\;\;\;H_j^{\left( {{c_7} + {g_7}{S_j}} \right)}CW_j^{\left( {{d_7} + {h_7}{S_j}} \right)} + {\varepsilon _{7j}};\\ 总生物量{W_{1j}} = \left( {{a_3} + {e_3}{S_j}} \right)D_j^{\left( {{b_3} + {f_3}{S_j}} \right)}\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;H_j^{\left( {{c_3} + {g_3}{S_j}} \right)}CW_j^{\left( {{d_3} + {h_3}{S_j}} \right)} + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left( {{a_4} + {e_4}{S_j}} \right)D_j^{\left( {{b_4} + {f_4}{S_j}} \right)}\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;H_j^{\left( {{c_4} + {g_4}{S_j}} \right)}CW_j^{\left( {{d_4} + {h_4}{S_j}} \right)} + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left( {{a_6} + {e_6}{S_j}} \right)D_j^{\left( {{b_6} + {f_6}{S_j}} \right)}\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;H_j^{\left( {{c_6} + {g_6}{S_j}} \right)}CW_j^{\left( {{d_6} + {h_6}{S_j}} \right)} + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left( {{a_7} + {e_7}{S_j}} \right)D_j^{\left( {{b_7} + {f_7}{S_j}} \right)}\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;H_j^{\left( {{c_7} + {g_7}{S_j}} \right)}CW_j^{\left( {{d_7} + {h_7}{S_j}} \right)} + {\varepsilon _{1j}}. \end{array} $ | (33) |
利用一元模型: 模型(28)(不考虑林分起源)和(29)(考虑林分起源),二元模型: 模型(30)(不考虑林分起源)和(31)(考虑林分起源)和三元模型: 模型(32)(不考虑林分起源)和(33)(考虑林分起源)对建模数据进行预测,得到的评价指标见表 3。
|
|
从表 3中可得出,对于不考虑林分起源情形,模型(28),(30)和(32)得到的树冠、树枝和树叶生物量的估计值偏高,对于地上总生物量,模型(28)和(30)得到的估计值高于真实值,而模型(32)得到的估计值低于真实值。对于树干、干材和和干皮生物量,除模型(28)估计出的树干和干材生物量偏高外,其他方法得到的各分量估计值都低于真实值。根据总相对误差可知,无论是一元模型还是二元或多元模型,对树冠和树叶预测精度较低,而对地上总生物量、干材和干皮预测精度较高。总体而言,二元生物量模型,即模型(30)对不考虑林分起源相容性生物量预测时精度最高。
对于考虑林分起源情形,模型(29)和(33)预测出的各分量生物量值高于真实值,模型(31)预测地上总生物量、树冠、树枝和树叶生物量时偏高,预测树干、干材和干皮生物量时偏低。与不考虑林分起源情形类相似,在利用一元、二元和三元模型预测各分量生物量时,树叶、树冠和树枝精度最高,而地上总生物量、树干和干材精度较高。总体而言,二元生物量模型,即模型(31)对考虑林分起源相容性生物量预测时精度最高。
4 结论与讨论解决相容性问题,一直是生物量估计领域的一个难题。本文利用比例平差法、非线性似然无关回归法和非线性联立方程组法构建相容性生物量模型,按照分配层次不同,非线性联立方程组法和比例平差法同时考虑总量直接控制和分级联合控制2种不同方案。从附表 1~3中可知,比例平差法拟合精度和模型稳定性总体上比非线性联立方程组要差,这可能是因为比例平差法涉及的各分量独立模型是通过传统的最小二乘回归求得参数计算各分量生物量。显然,各分量独立模型是在不考虑相容性的情况下给出参数的最优估计,因此在考虑相容性后可能就不再是最优估计。非线性似然无关回归法是通过对各分量生物量相加解决相容性问题(Parresol,2001),因此预测精度相对较高(附表 1~3)。但由于该方法参数是基于非线性似然无关理论估计得到,计算时对参数初始值依赖较大(Parresol,2001),如果参数的初始值给定不合理时,则计算很难达到收敛。而本文提出的非线性联立方程组是将各分量进行联合建模,联立求解,既保证了各分量生物量之间的相容性,又能得到更优化的参数估计。总体而言,非线性联立方程组法在拟合精度和模型稳定性方面比其他几种方法要好,尤其是总量控制联立方程组法,通过检验数据进一步验证该方法预测精度最高(表 3)。
本研究选用了5种林分因子,分别为胸径、地径、树高、枝下高以及冠幅作为构建相容性生物量模型的候选协变量。通过分析得知,胸径、树高和枝下高对各分量生物量影响较大,其中胸径影响最大,其次是树高和枝下高,这与Parresol(2001)和曾伟生等(2010b)研究结果一致。因此最终选择胸径、胸径和树高以及胸径、树高和枝下高分别作为一元、二元和三元模型中的协变量。通过对各方法中的一元、二元和三元模型预测效果进行比较(附表 1~3),总体而言,各分量对应的三元模型预测精度最高,其次是二元,最低是一元。实际应用时还可选择其他的林分变量进行分析,例如地径和冠长率。理论上讲,模型中协变量越多,模型精度越高。但由于一元、二元和三元模型之间预测精度尽管有差异,但是这种差异非常小,因此模型中考虑3个林分变量已能满足实际应用。
实际情况中,在相同直径或树高下,人工林树木的生物量和天然林树木的生物量可能相差较大。为此,本研究分别对不考虑林分起源和考虑林分起源的马尾松相容性生物量进行建模。其中,不考虑林分起源的相容性生物量模型是反映总体的平均变量情况;而考虑林分起源的相容性生物量模型,以模型(31)为例,把林分起源作为哑变量,通过参数c,d和f的大小可以反映人工林和天然林之间差异的大小,而参数a,b和e相当于固定效应,即不管是天然林和人工林,它们的取值都不变。通过实例分析可知,这种构建哑变量方法能有效解决不同起源的生物量相容性通用模型。除利用哑变量方法能有效解决模型通用性问题外,近代统计学模型中的非线性混合效应模型也能解决此类问题,基于目前还没有相应的算法和程序求解非线性混合效应模型联立方程组,因此无法保证生物量相容性问题。总之,到目前为止,通过构造哑变量方法构建不同起源相容性生物量通用性模型能得到可靠结果。
本文主要是对马尾松地上部分生物量进行研究,对于地下生物量以及总生物量同样可以利用本研究中所提出的方法进行建模。除生物量外,其他生态上所涉及总量分解成不同大小单元、或不同大小单元聚集成总体的物质特性,这些方法都实用。
|
|
|
|
|
|
|
|
| [1] |
符利勇,李永慈,李春明,等.2011b.基于两水平非线性混合模型对杉木林优势高生长量研究.林业科学研究,24(6): 720-726.( 2) 2)
|
| [2] |
符利勇,曾伟生,唐守正.2011a.利用混合模型分析地域对国内马尾松生物量的影响.生态学报,31(19): 5797-5808.( 2) 2)
|
| [3] |
李海奎,宁金魁.2012.基于树木起源、立地分级和龄组的单木生物量模型.生态学报,32(3): 740-757.( 1) 1)
|
| [4] |
骆期邦,曾伟生,贺东北,等.1999.立木地上部分生物量模型的建立及其应用研究.自然资源学报,14(3): 271-277.( 2) 2)
|
| [5] |
唐守正,郎奎建,李海奎.2008.统计和生物数学模型计算(ForStat教程).北京:科学出版社.( 1) 1)
|
| [6] |
唐守正,张会儒,胥辉.2000.相容性生物量模型的建立及其估计方法研究.林业科学,36(sp1): 19-27.( 5) 5)
|
| [7] |
曾伟生,唐守正.2010b.利用度量误差模型方法建立相容性立木生物量方程系统.林业科学研究,23(6): 797-802.( 3) 3)
|
| [8] |
曾伟生,唐守正.2010a.利用混合模型方法建立全国和区域相容性立木生物量方程.中南林业调查规划,29(4): 1-6.( 2) 2)
|
| [9] |
Basuki T M,van Laake P E,Skidmore A K,et al.2009.Allometric equations for estimating the above-ground biomass in tropical lowland Dipterocarp forests.For Ecol Manage,257(8): 1684-1694.( 1) 1)
|
| [10] |
Bi H,Turner J,Lambert M J.2004.Additive biomass equations for native eucalypt forest trees of temperate Australia.Trees,18(4): 467-479.( 3) 3)
|
| [11] |
Fehrmann L,Lehtonen A,Kleinn C,et al. 2008.Comparison of linear and mixed-effect regression models and a k-nearest neighbor approach for estimation of single-tree biomass.Can J For Res,38: 1-9.( 2) 2)
|
| [12] |
Fu L Y,Zeng W S,Tang S Z,et al.2012.Using linear mixed model and dummy variable model approaches to construct compatible single-tree biomass equations at different scales- a case study for masson pine in southern China.J For Sci,58(3):101-115.( 2) 2)
|
| [13] |
Jenkins J C,Chojnacky D C,Heath L S,et al.2003.National-scale biomass estimators for United States tree species.For Sci,49(1):12-35.( 1) 1)
|
| [14] |
Kittredge J.1944.Estimation of the amount of foliage of trees and stand.J For,42(12):905-912.( 1) 1)
|
| [15] |
Parresol B R.2001.Additivity of nonlinear biomass equations.Can J For Res,31(5): 865-878.( 9) 9)
|
| [16] |
Tang S Z,Zhang H R,Xu H.2000.Study on establish and estimate method of compatible biomass model.Scientia Silvae Sinicae,36(supple.1): 19-27.( 1) 1)
|
| [17] |
Vallet P,Dhte J F,Moguédec G L,et al.2006.Development of total aboveground volume equations for seven important forest tree species in France.For Ecol Manage,229(1/3): 98-110.( 1) 1)
|
| [18] |
Waring R H,Running S W.1998.Forest ecosystems: analysis at multiple scales.2nd ed.Academic Press,San Diego,Calif.( 1) 1)
|
| [19] |
Zeng W S,Tang S Z.2010.Using measurement error modeling method to establish compatible single-tree biomass equations system.Forest Research,23(6): 797-802.( 1) 1)
|
| [20] |
Zeng W S,Tang S Z.2012.Modeling compatible single-tree biomass equations of masson pine(Pinus massoniana)in southern China.J For Res,23(4): 593-598.( 2) 2)
|
| [21] |
Zeng W S,Zhang H R,Tang S Z.2011.Using the dummy variable model approach to construct compatible single-tree biomass equations at different scales-a case study for masson pine(Pinus massoniana)in southern China.Can J For Res,41(7): 1547-1554.( 2) 2)
|
| [22] |
Zhang Y J,Borders B E.2004.Using a system mixed-effects modeling method to estimate tree compartment biomass for intensively managed loblolly pines-an allometric approach.For Ecol Manage,194(1/3): 145-157.( 2) 2)
|
 2014, Vol. 50
2014, Vol. 50