文章信息
- 徐华东, 徐国祺, 王立海, 杨学春
- Xu Huadong, Xu Guoqi, Wang Lihai, Yang Xuechun
- 原木横截面应力波传播时间等值线绘制及影响因素分析
- Construction of Stress Wave Time Isolines on Log Cross Section and Analysis of Its Effect Factors
- 林业科学, 2014, 50(4): 95-100
- Scientia Silvae Sinicae, 2014, 50(4): 95-100.
- DOI: 10.11707/j.1001-7488.20140414
-
文章历史
- 收稿日期:2013-05-20
- 修回日期:2013-11-17
-
作者相关文章
横截面是立木的一个典型断面。在横截面上,木材的各表征指标均有不同程度的变化,包括年轮宽度、含水率、密度、木射线组织比率和早晚材比率等(刘一星等,2004),这些因素会对应力波传播产生影响。利用应力波设备,检测活立木及原木内部腐朽缺陷时,通常根据测试对象内的应力波传播速度构造速度矩阵,构建横截面应力波二维图像并分析其变化,这是当前定性、定量判断活立木及原木内部腐朽、空洞等缺陷的主要方法之一(安源等,2008; 梁善庆等,2008; 王立海等,2001; 王志同等,1995)。应力波在横截面的传播规律研究是活立木及原木内部缺陷辨识的基础,因此研究横截面内应力波传播规律非常有意义。
近几年,国内外学者采用应力波方法对活立木、原木、木结构立柱等对象的内部腐朽进行了较广泛的应用研究(安源等,2008; 陈勇平等,2012; 吴福社等,2011; Bucur,2005; Nicolotti et al.,2003),研究主要集中于应力波成像与腐朽之间的关系。然而,涉及应力波在活立木横截面内传播路径的研究相对较少,仅有张厚江等(2010)对美国红松(Pinus resinosa)原木中的应力波传播时间(SWT)等值线进行了试验研究,但该研究主要针对健康原木进行测试,未对木材缺陷进行分析。
本文将对健康和含空洞原木横截面的SWT等值线变化规律及影响因素开展试验研究,期望能够探明应力波在活立木及原木横截面的传播规律,为准确判定立木及原木的内部腐朽等缺陷提供基础。
1 材料与方法 1.1 试验材料试验树种为大青杨(Populus ussuriensis),取自哈尔滨方正林业局。结合林业局作业状况,在原木大头处取长10 cm的小段原木用作试验样本。选取样本时,要选没有节子和腐朽等缺陷的完好原木。原木样本周长为113 cm,长、短直径分别为37和35 cm。在测试期间,用塑料袋将原木样本包好,放在低温冰箱内保存,以防止含水率改变。
1.2 试验条件在实验室内测试,环境温度为20 ℃,空气相对湿度为72%。
主要采用匈牙利Fakopp公司生产的两通道应力波设备(Microsecond Timer)和德国RINNTECH公司生产的多通道仪器(Arbotom)对原木横截面内SWT进行测试(图 1)。
 |
图 1 样本横截面内各接收点应力波传播时间测试
Fig. 1 Stress wave time measurement through the cross section of log specimen
|
测试时,以髓心为中心,在样本横截面划分网格,间距3 cm。以O点为激励点,其他点依次为接收点,共101个,如图 1。测试每一点时,以相同力度用小锤敲击激励传感器5~10次,观察数据,待误差小于3 μs记录平均值。测试分3部分:
1)常温完好样本试验常温下,用小锤敲击完好样本激励点,激发信号,依次在各接收点接收信号,获取SWT数据。采用Matlab处理横截面内SWT矩阵,绘制SWT等值线。
2)低温完好样本试验常温样本试验后,将样本放入低温冷柜,改变其温度(分别为-5 ℃和-20 ℃),测试低温样本横截面内SWT数据,构建SWT矩阵,绘制SWT等值线。
3)含空洞样本试验常温下,以髓心为中心,在样本横截面内依次凿取不同直径(d分别为4,6,10,14,18和22cm)的圆孔。依据上述方法,测试样本含空洞时SWT数据,构建SWT矩阵并绘制等值线。
1.3.2 SWT等值线绘制方法采用网格布点法,对完好及含空洞样本测试后,得到每种情况下的SWT矩阵。然后,采用Matlab编程,绘制样本横截面内的SWT等值线。绘制SWT等值线主要分3步:
1)设定坐标系,确定坐标和SWT矩阵。坐标系确定方法: 原点设在原木样本的髓心; Y轴设定为激励点和髓心的连线方向; X轴设定为与Y轴垂直的方向(经过髓心)。依据建立的坐标系,计算横截面内各测点的坐标值; 然后,分析每种情况时,以SWT为 Z值,以矩阵的形式列出各测点的X,Y值和Z值,共145行3列。
2)确定绘图区域(正方形,含横截面),绘制并标注SWT等值线。建立坐标系后,按照SWT矩阵和坐标值,对X,Y轴上的点进行画格操作(meshgrid函数),对SWT矩阵二维插值(griddata命令),绘制等值线(contour函数),即可得到平滑曲线。最后,采用定义标注向量的方法,标注等值线(clable命令)。
3)确定横截面和圆孔边界。对于完好样本,需要定义横截面的边界。步骤包括: ①设定横截面的半径,定位横截面外面的数值(find函数),令它们为空值(NaN); ②在等值线上,添加圆孔边界(plot命令)。对含圆孔样本,完成上述工作后,还需定位空洞的边界,进而绘制圆孔。
2 结果与分析 2.1 原木横截面SWT等值线规律从激励点到完好样本横截面上各接收点的SWT数据,见图 2。利用Matlab对图 2中数据进行处理,得到完好原木样本横截面的SWT等值线(图 3)。图 3显示,在横截面内,以圆弧形曲线,应力波从激励点向各接收点逐渐传播,径向传播较快,弦向传播较慢。这与王立海等(2011)研究弦向角对应力波传播影响所得结论一致,Wang(1999)、Wang等(2004)的相关研究也得到类似结论。同时,图 3还表明,在各方向上,应力波传播曲线平滑,传播稳定。
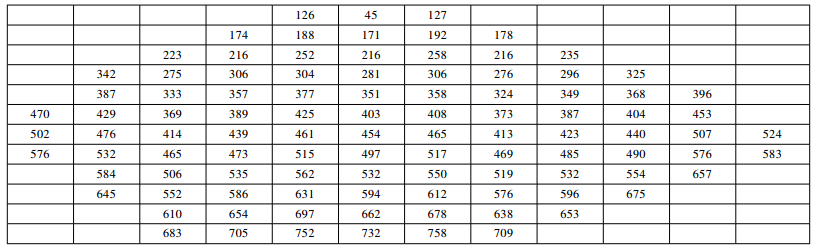 |
图 2 常温完好样本横截面内各接收点所得应力波传播时间(Arbotom 测试)
Fig. 2 SWT data captured by each measuring point on the log section(Arbotom test)
|
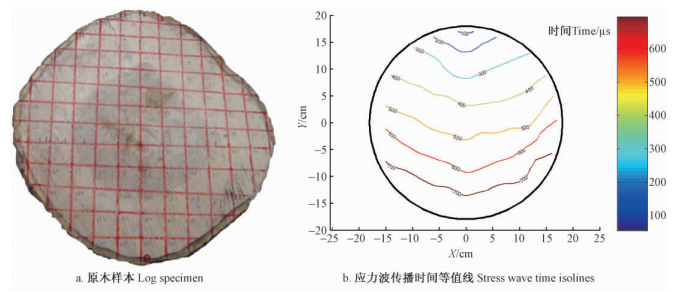 |
图 3 温度20 ℃时完好样本横截面应力波传播时间等值线
Fig. 3 SWT isolines of log specimen at 20 ℃ temperature
|
在原木横截面内,为分析温度变化对应力波传播规律的影响,采用应力波设备逐点测试了低温样本(-5 ℃和-20 ℃)中从激励点到横截面内各接收点的SWT数据,绘制了SWT等值线(图 4)。图 4表明,低温与常温相比,相同之处在于: 在完好原木横截面,SWT等值线均为平滑圆弧曲线,从激励点向各接收点逐渐传播。径向上,应力波传播快; 而在弦向,传播较慢。二者相比,不同之处在于: 在低温样本中,不论哪个方向,应力波传播速度均更快。
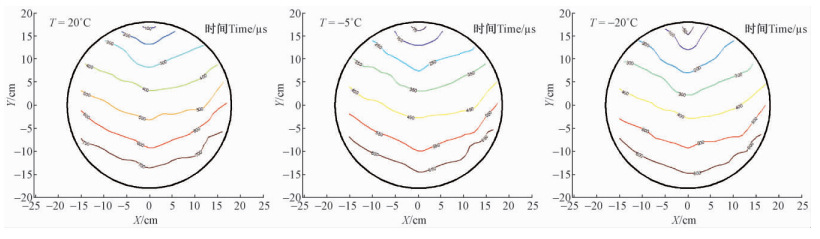 |
图 4 不同温度时完好样本横截面应力波传播时间等值线
Fig. 4 SWT isolines of log specimen at various temperatures
|
图 5显示了不同温度完好样本应力波传播速度与弦向角之间的关系[关于弦向角的定义,见王立海等(2011)]。图 5表明,不同温度时,应力波速度随弦向角增大的变化趋势类似,随弦向角增大,应力波传播速度逐渐增大。当弦向角达到90°时,应力波速度达到最大值。图 5中,趋势线是依据王立海等(2011)中大青杨应力波速度数据所绘制的,期间将Fakopp测试数据转化为Arbotom数据。
 |
图 5 不同温度完好样本应力波传播速度与弦向角之间的关系
Fig. 5 Relation between stress wave velocity and tangential angle of log specimen at different temperatures
|
常温与低温相比,不同之处主要在于低温原木样本的应力波传播数值更高。依据图 5中Arbotom测得数据可知,常温20 ℃时原木样本径向应力波传播速度为747 m·s-1,而原木样本在-5 ℃和-20 ℃时对应值分别为926 m·s-1和1005 m·s-1。引起冻结原木中应力波传播速度加快的主要原因是: 在0 ℃以下,原木中水分状态发生了改变(徐华东等,2012),所含自由水和部分结合水由水变成冰,而固态冰中应力波传播速度(3988 m·s-1)要远高于水中传播速度(1473 m·s-1)。
2.3 空洞对原木横截面SWT等值线的影响图 6列出了常温含空洞3(d=10 cm)样本横截面上SWT数据,图 7为对应的SWT等值线。由于数据较多,仅以含空洞3样本的应力波数据予以说明。
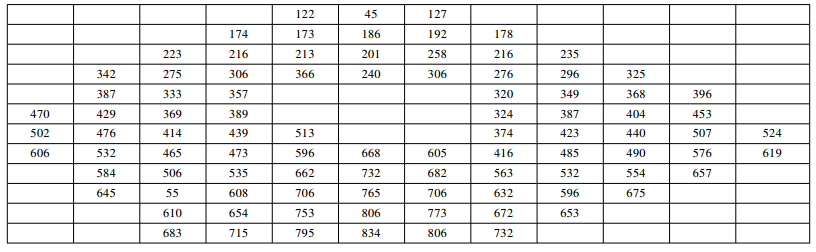 |
图 6 常温含空洞3(d = 10 cm)原木横截面内各接收点应力波传播时间(Arbotom 测试)
Fig. 6 SWT data received by each points on the cross section of log specimen containing cavity 3(Arbotom test)
|
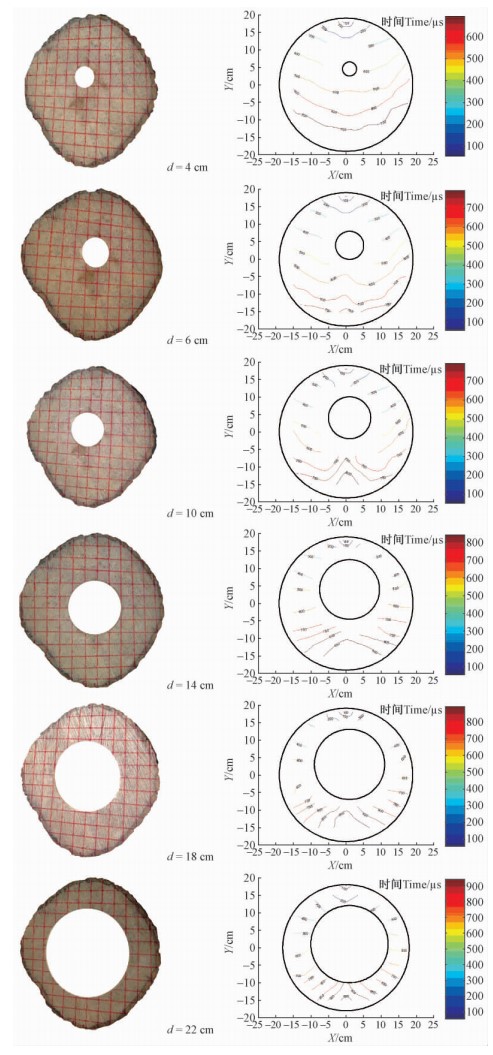 |
图 7 含不同尺寸空洞样本的应力波传播时间等值线
Fig. 7 SWT isolines of log specimen with different size cavity
|
对比图 3和图 7可知,空洞对SWT等值线有显著影响。在完好样本横截面,从激励点开始,应力波按照圆弧曲线向各接收点传播。在传播过程中,径向传播快,弦向较慢。而在含空洞样本横截面,SWT等值线发生较显著变化,在未到达空洞之前,应力波传播形状为圆弧; 当遇到空洞后,其传播路径发生改变,应力波绕着空洞传播,即沿空洞周围木材传播(徐华东,2011),其SWT等值线分成2段; 当应力波穿过空洞后,它不再以圆弧曲线继续传播,而形成一个SWT的“滞后”,等值线形状则变为带有“凹槽”。这表明,空洞对应力波在原木横截面的传播路径产生了影响,导致其传播路径延长,促使SWT增加。
对不同直径圆孔样本的SWT等值线(图 5)比较可知,空洞大小对SWT等值线影响较显著。当d=4 cm时,与完好样本比,空洞后SWT等值线变化不明显,仍以圆弧形传播。但是,随直径d增大,空洞后的SWT等值线变化逐渐变大。当d=6 cm时,空洞后SWT等值线曲线出现小的“凹槽”或“滞后”; 当d=14 cm时,空洞后SWT等值线发生较大变化,不再是“径向快,弦向慢”的规律,而是变为“弦向快,径向慢”,SWT等值线形成一个显著的“凹槽”,形似“倒圆弧曲线”。
不仅SWT等值线形状差别明显,而且其标注值变化也非常显著。随直径d增大,传播到空洞后面区域的SWT数值在逐渐增加,在木材径向这一趋势表现得更为明显。在横截面内,空洞会促使应力波传播路径(包括径向和弦向)发生改变,延长其传播时间。由于SWT数值在径向变化较明显,并且它是活立木(原木)健康评价的重要指标,因此分析空洞大小对原木样本径向SWT数值的影响很有必要。
图 8为径向SWT数值与空洞直径d的关系图。图 8显示,随直径d增大,径向SWT逐渐增大。当d<6 cm时,径向SWT增长幅度较小,d=6 cm时SWT=762 μs,比完好样本(d=0 cm,SWT=732 μs)高30 μs。当d>6 cm后,径向SWT时间增长幅度逐渐变大。d=10 cm时,SWT=834 μs,比完好样本对应数值高102 μs,增大比例为14%; 而d=22 cm时,对应值高236 μs,增大比例为32%。
 |
图 8 空洞直径对径向应力波传播时间的影响
Fig. 8 Relationship between cavity diameter and SWT
|
1)在完好原木横截面,从激励点开始,应力波以圆弧形曲线向各测点逐渐传播。径向上传播快,弦向上传播较慢。
2)与常温相比,应力波在低温原木中传播更快。低温与常温原木横截面应力波传播时间等值线分布规律类似。
3)空洞对原木横截面SWT等值线具有显著影响。与完好原木不同,应力波在含空洞原木横截面传播时,空洞后会产生一个SWT的“滞后”。对于SWT等值线,其形状显示为带有“凹槽”。这表明,空洞改变了原木横截面的应力波传播路径,导致其路径延长,促使SWT增加。空洞直径与传播到空洞后面区域的SWT数值正相关,木材径向的相关系数尤其高。
| [1] |
安 源, 殷亚方, 姜笑梅, 等. 2008. 应力波和阻抗仪技术勘查木结构立柱腐朽分布. 建筑材料学报, 11(4): 457-463.( 2) 2)
|
| [2] |
陈勇平, 刘秀英, 李 华, 等. 2012. 不同数量传感器下云杉模拟缺陷材应力波成像规律探讨. 林业科学, 48(4): 97-101.( 1) 1)
|
| [3] |
梁善庆, 王喜平, 蔡智勇, 等. 2008.弹性波层析成像技术检测活立木腐朽. 林业科学, 44(5): 109-114.( 1) 1)
|
| [4] |
刘一星, 赵广杰. 2004. 木质资源材料学. 北京: 中国林业出版社, 77-82.( 1) 1)
|
| [5] |
王立海, 王 洋, 徐华东. 2011. 弦向角对应力波在原木横断面传播速度的影响. 林业科学, 47(8): 139-142.( 3) 3)
|
| [6] |
王立海, 杨学春, 徐凯宏. 2001. 木材缺陷无损检测技术研究现状与进展. 森林工程, 17(6): 1-3.( 1) 1)
|
| [7] |
王志同, 曹志强, 袁卫国. 1995. 用应力波非破损检测技术检测中密度纤维板弹性模量的研究. 木材工业, 9(5): 17-19.( 1) 1)
|
| [8] |
吴福社, 吴贻军, 邵卓平. 2011. 应力波仪和阻力仪用于雪松立木内部材性检测的研究. 安徽农业大学学报, 38(1): 127-130.( 1) 1)
|
| [9] |
徐华东, 王立海. 2012. 冻结红松和大青杨湿木材内部水分存在状态及含量测定. 林业科学, 48(2): 139-143.( 1) 1)
|
| [10] |
徐华东. 2011. 冻结与非冻结木材中应力波传播速度规律研究. 哈尔滨: 东北林业大学博士学位论文.( 1) 1)
|
| [11] |
张厚江, 王喜平, 苏 娟, 等. 2010. 应力波在美国红松立木中传播机理的试验研究. 北京林业大学学报, 32(2): 145-149.( 1) 1)
|
| [12] |
Bucur V. 2005. Ultrasonic techniques for nondestructive testing of standing trees. Ultrasonics, 43(4): 237-239.( 1) 1)
|
| [13] |
Nicolotti G, Socco L V, Martinis R, et al. 2003. Application and comparison of three tomographic techniques for detection of decay in trees. Journal of Arboriculture, 29(2): 66-78.( 1) 1)
|
| [14] |
Wang X P. 1999. Stress Wave-based nondestructive evaluation(NDE)methods for wood quality of standing trees. A doctoral dissertation of Michigan Technological University.( 1) 1)
|
| [15] |
Wang X P, Divos F, Pilon C, et al. 2004. Assessment of decay in standing timber using stress wave timing nondestructive evaluation tools. A guide for use and interpretation. Gen. Tech. Rep. FPL-GTR-147. Madison, WI: U.S. Department of Agriculture, Forest Service, Forest Products Laboratory, 12.( 1) 1)
|
 2014, Vol. 50
2014, Vol. 50

