对于稀少、群团状的总体，自适应群团抽样(adaptive cluster sampling，简称ACS)被认为是一种有效的估计，采用适应性抽样的设计比传统的抽样设计能获得更小的方差、更有效(Thompson，1990; 朱光玉等，2010a; 2010b; 2011; Seber et al.，1994; Thompson et al.，1996)。自从Thompson(1990)提出自适应群团抽样设计以来，该方法被广泛应用于生态学、林学、生物学、流行病学、环境科学、人口统计学和地质学等各个领域(Thompson，1990; Brown，1994; Seber et al.，1994; Thompson et al.，1996; Dryver et al.，1998; 张南松等，2000; 雷渊才等，2007; 朱光玉等，2010a; 2010b; 2011)。

影响自适应群团抽样设计的效率有多种因素，包括抽样设计的选择(简单随机抽样、分层抽样、两阶段抽样等)(Christman，2000)、网络结构的变化(Smith et al.，1995; Brown，1996; Thompson et al.，1996; Christman，1996a; 1996b)、网络数和网络大小(Brown，2003)、临界值的大小(Christman，1996b; 1997; Christman，2000; Smith et al.，2003)、邻域的定义(Brown，1994; Christman，1996b; 1997; Christman，2000; Brown，2003)、估计量的类型(Christman，1996b; 1997; Salehi，2003; Felix-Medina，2003)、单元大小(Christman，1996b; 1997)等。

稀少、群团状分布的植被是森林资源的重要组成部分，在采用自适应群团抽样估计这类森林资源总体时，不仅要考虑抽样调查的效率，而且要考虑抽样调查的成本。其中一个比较现实的问题就是在外业调查中调查单元面积大小的选取，针对不同的植被类型，样本单元多大比较合适？在初始样本量一定的前提下，样本单元越大，获取的抽样信息越多，抽样精度越高，同时抽样调查成本也会越高。基于此，本文针对乔木和灌木物种进行了自适应群团抽样模拟试验，设计了4种不同单元大小，利用变动系数，针对乌兰布和沙漠边缘典型的稀少、群团状植被(灌木和小乔木)进行了模拟研究与分析，对灌木和小乔木适宜单元面积大小的选取进行了探索，提出了灌木和小乔木物种自适应群团抽样适宜单元面积的大小，为稀少、群团状分布的森林资源外业调查样本单元大小的选取提供理论依据。

研究地点位于内蒙古自治区磴口县境内，地处内蒙古西部，属于黄河河套地区，灌溉农业发达，境内自然环境分割明显，西部为沙漠戈壁。研究区选在内蒙古西部磴口县巴彦高勒镇西南约8 km黄河西岸绿洲向乌兰布和沙漠过渡的沙漠区，中心点坐标为40°15'37.8″N，106°56'28.0″E，位于农垦区与沙漠交界处，分布有典型的沙地植被，是林业治沙技术试验区。根据研究区的生态系统结构、功能及其环境特点，在研究区选择具有典型代表性质的稀少且呈群团状的沙漠植被类型。研究区主要乔木树种有沙枣(Elaeagnus angustifolia)，沙枣为人工林;主要灌木树种有白刺(Nitraria tangutorum)、梭梭(Haloxylon ammodendron)、柽柳(Tamarix chinensis)、花棒(Hedysarum scoparium)、盐爪爪(Kalidium foliatum)、柠条锦鸡儿(Caragana korshinskii)和沙蒿(Artemisia ordosica)等;主要草本植物有沙米(Agriophyllum squarrosum)、芦苇(Phragmites australis)和沙鞭(Psammochloa villosa)沙地旋覆花(Inula salsoloides)等(周培荣，1998)。

以花棒、柽柳、沙枣作为研究总体，其目标变量为植被株数，总体面积为100 hm²。3种植被的坐标位置分布见图 1，2，3，对于单株，就是该株的坐标，对于丛状多株植被，则代表该丛植被的中心坐标。表 1，2和3表示3种总体在4种不同样本单元面积划分下的总体单元个数与单元平均值。

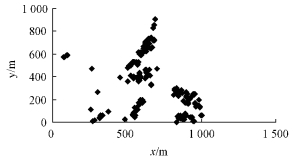	图 1 花棒分布 Fig. 1 Distribution of Hedysarum scoparium

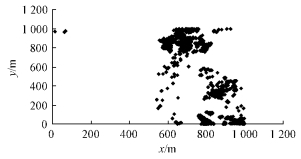	图 2 柽柳分布 Fig. 2 Distribution of Tamarix chinensis

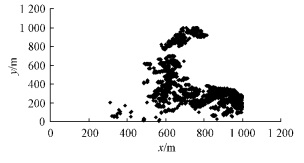	图 3 沙枣分布 Fig. 3 Distribution of Elaeagnus angustifolia

表 1 花棒模拟试验总体参数 Tab.1 Simulation population experiment parameters of Hedysarum scoparium

表 1 花棒模拟试验总体参数 Tab.1 Simulation population experiment parameters of Hedysarum scoparium 单元面积 Unit area/m2 总体总值 Population total (number of plants) 总体单元均值 Population mean (number of plants) 总体单元数 Population size 5×5 2 107 0.052 68 40 000 10×10 2 107 0.210 70 10 000 10×20 2 107 0.421 40 5 000 20×20 2 107 0.842 80 2 500

表 2 柽柳模拟试验总体参数 Tab.2 Simulation population experiment parameters of Tamarix chinensis

表 2 柽柳模拟试验总体参数 Tab.2 Simulation population experiment parameters of Tamarix chinensis 单元面积 Unit area/m2 总体总值 Population total (number of plants) 总体单元均值 Population mean (number of plants) 总体单元数 Population size 5×5 14 374 0.359 35 40 000 10×10 14 374 1.437 40 10 000 10×20 14 374 2.874 80 5 000 20×20 14 374 5.749 60 2 500

表 3 沙枣模拟试验总体参数 Tab.3 Simulation population experiment parameters of Elaeagnus angustifolia

表 3 沙枣模拟试验总体参数 Tab.3 Simulation population experiment parameters of Elaeagnus angustifolia 单元面积 Unit area/m2 总体总值 Population total (number of plants) 总体单元均值 Population mean (number of plants) 总体单元数 Population size 5×5 6 995 0.174 875 40 000 10×10 6 995 0.699 500 10 000 10×20 6 995 1.399 000 5 000 20×20 6 995 2.798 000 2 500

针对研究区，在初始样本量相同的前提下，选取5种初始样本: n=50，n=100，n=150，n=200和n=250，均采用500次重复抽样次数。对4种不同的总体单元大小(总体单元面积分别为5 m×5 m，10 m×10 m，10 m×20 m，20 m×20 m)，采用最初样本不放回的基于Hansen-Hurwitz估计量和基于Horvitz-Thompson估计量的自适应群团抽样进行了模拟抽样。

基于修正Hansen-Hurwitz(HH)的均值估计为:

$ {\hat \mu _{{\text{HH}}}} = \frac{1}{{{n_1}}}\sum\limits_{i = 1}^{{n_1}} {{w_i}}， $

$ {\rm{\hat Var}}({\hat \mu _{{\text{HH}}}})= \frac{{N - {n_1}}}{{N{n_1}({n_1} - 1)}}\sum\limits_{i = 1}^{{n_1}} {{{({w_i} - {{\hat \mu }_{{\text{HH}}}})}^2}} . $

基于修正Horvitz-Thompson(HT)的均值估计为:

$ {\hat \mu _{{\text{HT}}}} = \frac{1}{N}\sum\limits_{i = 1}^N {\frac{{{y_i}{I_i}}}{{{\pi _i}}}}， $

$ {\rm{\hat Var}}({\hat \mu _{{\text{HT}}}}) = \frac{1}{{{N^2}}}\left[ {\sum\limits_{j = 1}^K {\sum\limits_{k = 1}^K {y_j^*y_k^*(\frac{{{\pi _{jk}} - {\pi _j}{\pi _k}}}{{{\pi _j}{\pi _k}}}){I_j}{I_k}} } } \right]. $

上述公式中相关的参数含义及其具体计算见Thompson(1990)。其中n₁ 为初始样本单元; w_i为单元i所在的网络均值; N为总体单元数; y_i为单元i所在的网络单元值之和; y_j^*与y_k^*分别表示单元j和k所在的网络单元值之和; I_i，I_j和I_k表示单元i，j和k是否被选中的随机变量，选中则为1，否则等于0;π_i，π_j和π_k表示单元i，j和k所在网络的包含概率; π_jk表示单元j和k的联合交叉包含概率。

重复抽样次数(times of resampling)简称重复次数，用rep表示，第i次重复抽样的均值估计量及其方差估计量用μ_i和v_i(i=1，2，…，rep)表示。$E({\mu _i})= \sum\nolimits_{i = 1}^{{\text{rep}}} {{\mu _i}/{\text{rep}}} $表示重复抽样所得均值估计量的均值，$E({v_i})= \sum\nolimits_{i = 1}^{{\text{rep}}} {{v_i}/{\text{rep}}} $表示重复抽样所得v_i的均值。E(v_i)的数值越小，抽样精度越高。

变动系数(variation coefficient，简称 CV)定义如下:

$ \begin{gathered} {\text{C}}{{\text{V}}^2} = E({v_i})/{E^2}({\mu _i}); \hfill \\ {\text{CV}} = \sqrt {E({v_i})/{E^2}({\mu _i})} . \hfill \\ \end{gathered} $

同一抽样总体，当初始样本量相同、单元面积大小不同时，所抽取的单元包含的总体信息也不一致。通常，单元面积越大，所包含的总体信息越多，抽样精度越高，抽样效果越好，随着抽样单元面积的增加，变动系数将变小，渐渐趋于一个稳定的常数。然而单元面积越大，所产生的外业调查经费也会越高。因此，对于同一种抽样方法，抽样调查精度与费用往往是相互矛盾的。当抽样单元面积大小增加到一定程度时，会出现一个转折点(或者区间)，在此点(或区间)之前，随着单元面积大小的增加，抽样精度会急剧增加，在这个点(区间)之后，随着抽样单元面积大小的增加，抽样精度增加幅度会很小，甚至趋于零。因此，利用此点(或者区间)，可以找到适宜的抽样单元面积大小。

对研究区1 km²分布稀少、群团状的典型灌木花棒和柽柳与乔木沙枣，在初始样本量相同的前提下，设计4种不同的总体单元大小(5 m×5 m，10 m×10 m，10 m×20 m，20 m×20 m)，采用最初样本不放回的基于Hansen-Hurwitz估计量自适应群团抽样(HHACS)和基于Horvitz-Thompson估计量的自适应群团抽样(HTACS)进行了模拟抽样，得到重复抽样的均值和方差估计。基于此，从变动系数入手，对变动系数与样本单元面积大小的相关关系进行分析研究。

选取初始样本量n=250进行模拟试验，2种抽样方法的模拟抽样均值估计结果见表 4。基于Hansen-Hurwitz估计量自适应群团抽样的模拟结果表明:对于花棒，其均值估计相对误差绝对值最大值为4.62%，最小值为0.19%; 对于柽柳，其均值估计相对误差绝对值最大值为2.00%，最小值为0.03%; 对于沙枣，其均值估计相对误差绝对值最大值为1.00%，最小值为0.28%。基于Horvitz-Thompson估计量的自适应群团抽样的模拟结果表明:对于花棒，其均值估计相对误差绝对值最大值为6.14%，最小值为1.40%; 对于柽柳，其均值估计相对误差绝对值最大值为1.82%，最小值为0.78%; 对于沙枣，其均值估计相对误差绝对值最大值为0.67%，最小值为0.24%。

表 4 3种植被样本单元株数密度均值估计 Tab.4 Mean density estimator for three kinds of vegetation

表 4 3种植被样本单元株数密度均值估计 Tab.4 Mean density estimator for three kinds of vegetation 单元面积 Unit size/m2 初始样本量 Initial sample size 花棒Hedysarum scoparium 柽柳Tamarix chinensis 沙枣Elaeagnus angustifolia $E({{\hat \mu }_{{\text{HH}}}})$ $E({{\hat \mu }_{{\text{HT}}}})$ $E({{\hat \mu }_{{\text{HH}}}})$ $E({{\hat \mu }_{{\text{HT}}}})$ $E({{\hat \mu }_{{\text{HH}}}})$ $E({{\hat \mu }_{{\text{HT}}}})$ 25 250 0.050 24 0.049 44 0.351 86 0.352 78 0.176 76 0.176 04 100 250 0.211 09 0.207 74 1.413 88 1.419 44 0.713 39 0.703 50 200 250 0.405 80 0.396 49 2.852 07 2.850 88 1.402 94 1.403 41 400 250 0.840 16 0.811 01 5.751 27 5.704 38 2.779 15 2.791 30

2种抽样方法的模拟抽样均值方差估计结果见表 5。基于Hansen-Hurwitz估计量自适应群团抽样的模拟结果表明:对于花棒，其均值方差估计值最大值为0.073 62，最小值为0.003 30; 对于柽柳，其均值估计相对误差绝对值最大值为1.359 41，最小值为0.030 36; 对于沙枣，其均值估计相对误差绝对值最大值为0.163 66，最小值为0.003 21。基于Horvitz-Thompson估计量的自适应群团抽样的模拟结果表明:对于花棒，其均值估计相对误差绝对值最大值为0.053 30，最小值为0.003 26; 对于柽柳，其均值估计相对误差绝对值最大值为0.216 02，最小值为0.026 29; 对于沙枣，其均值估计相对误差绝对值最大值为0.012 01，最小值为0.002 30。

表 5 3种植被样本单元株数密度均值方差估计 Tab.5 Mean density variance estimator for three kinds of vegetation

表 5 3种植被样本单元株数密度均值方差估计 Tab.5 Mean density variance estimator for three kinds of vegetation 单元面积 Unit size/m2 初始样本量 Initial sample size 花棒Hedysarum scoparium 柽柳Tamarix chinensis 沙枣Elaeagnus angustifolia ${{E[{\rm{\hat Var}}}}({{\hat \mu }_{{\text{HH}}}})]$ ${{E[{\rm{\hat Var}}}}({{\hat \mu }_{{\text{HT}}}})]$ ${{E[{\rm{\hat Var}}}}({{\hat \mu }_{{\text{HH}}}})]$ ${{E[{\rm{\hat Var}}}}({{\hat \mu }_{{\text{HT}}}})]$ ${{E[{\rm{\hat Var}}}}({{\hat \mu }_{{\text{HH}}}})]$ ${{E[{\rm{\hat Var}}}}({{\hat \mu }_{{\text{HT}}}})]$ 25 250 0.003 30 0.003 26 0.030 36 0.026 29 0.003 21 0.002 30 100 250 0.016 18 0.015 36 0.178 56 0.087 65 0.027 08 0.012 01 200 250 0.033 12 0.028 71 0.474 76 0.172 54 0.063 18 0.011 07 400 250 0.073 62 0.053 30 1.359 41 0.216 02 0.163 66 0.007 20

选取5种初始样本: n=50，n=100，n=150，n=200和n=250，由模拟抽样对总体均值估计和方差估计，结合$E({v_i})= \sum\nolimits_{i = 1}^{{\text{rep}}} {{v_i}/{\text{rep}}} $4，可以得到4种不同样本单元面积大小、2种自适应群团抽样估计的变动系数(表 6)。

表 6 变动系数与样本单元大小的相关关系^① Tab.6 Relation of the variation coefficient and sample unit size

表 6 变动系数与样本单元大小的相关关系① Tab.6 Relation of the variation coefficient and sample unit size 单元面积 Unit size/m2 初始样本量 Initial sample size 花棒Hedysarum scoparium 柽柳Tamarix chinensis 沙枣Elaeagnus angustifolia CV(HH) CV(HT) CV(HH) CV(HT) CV(HH) CV(HT) ①CV(HH)表示基于Hansen-Hurwitz估计量自适应群团抽样的变动系数,CV(HT)表示基于Horvitz-Thompson估计量的自适应群团抽样的变动系数。CV(HH) stands for variation coefficient of adaptive cluster sampling with Hansen-Hurwitz estimator,CV(HT) stands for variation coefficient of adaptive cluster sampling with Horvitz-Thompson estimator. 25 50 2.920 48 2.917 82 1.122 97 1.099 73 0.754 06 0.726 88 100 50 1.319 52 1.323 77 0.691 44 0.622 35 0.551 61 0.492 51 200 50 1.012 21 1.011 23 0.563 12 0.481 39 0.408 76 0.286 11 400 50 0.754 32 0.741 28 0.482 04 0.330 22 0.337 46 0.116 53 25 100 1.686 82 1.685 78 0.679 97 0.651 07 0.515 37 0.473 29 100 100 0.913 47 0.912 38 0.477 94 0.393 48 0.371 96 0.294 86 200 100 0.697 95 0.687 37 0.384 97 0.290 35 0.285 42 0.151 30 400 100 0.517 76 0.495 27 0.331 02 0.179 96 0.236 42 0.066 50 25 150 1.491 83 1.489 17 0.628 29 0.595 02 0.419 48 0.376 01 100 150 0.761 49 0.758 87 0.392 62 0.304 39 0.305 83 0.225 33 200 150 0.585 28 0.569 16 0.315 46 0.216 99 0.234 94 0.108 95 400 150 0.425 32 0.394 26 0.269 19 0.131 23 0.192 18 0.048 82 25 200 1.247 25 1.247 14 0.522 05 0.490 81 0.366 02 0.317 66 100 200 0.671 89 0.668 77 0.333 67 0.247 88 0.261 49 0.181 01 200 200 0.499 90 0.482 27 0.269 87 0.175 97 0.203 03 0.086 86 400 200 0.360 90 0.329 43 0.228 08 0.101 25 0.164 61 0.038 38 25 250 1.143 42 1.154 86 0.495 20 0.459 61 0.320 53 0.272 43 100 250 0.602 59 0.596 59 0.298 87 0.208 57 0.230 67 0.155 78 200 250 0.448 47 0.427 35 0.241 59 0.145 70 0.179 16 0.074 97 400 250 0.322 95 0.284 67 0.202 73 0.081 48 0.145 57 0.030 40

由表 6分析可知，随着单元面积的增加，变动系数发生有规律性的变化。由图 4，5，6，可以更加直观观测变动系数随单元面积的变化而变化的客观规律。

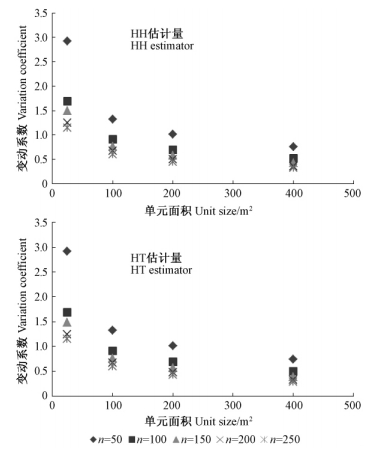	图 4 花棒变动系数 Fig. 4 Variation coefficient of Hedysarum scoparium

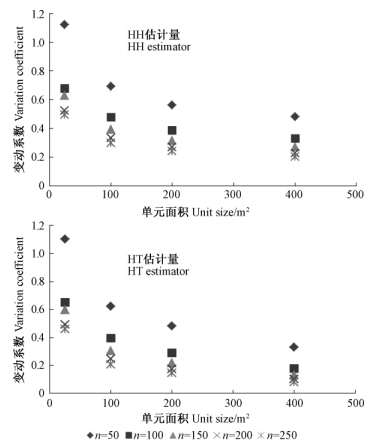	图 5 柽柳变动系数 Fig. 5 Variation coefficient of Tamarix chinensis

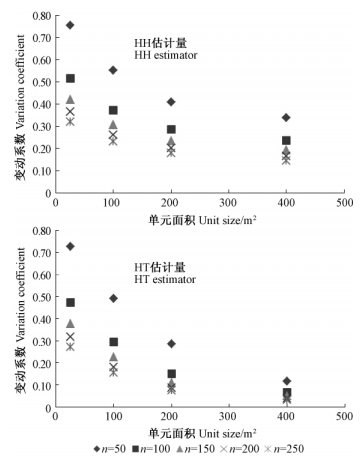	图 6 沙枣变动系数 Fig. 6 Variation coefficient of Elaeagnus angustifolia

图 4，5，6表明: 1)2种抽样方法的变动系数与单元大小的相关关系呈相同的变化趋势; 2)花棒和柽柳总体的模拟研究中，变动系数变化规律也是一致的，即变动系数随着样本单元面积的增加变动系数变小，样本单元面积小于100 m²时，变动系数随样本单元面积的增加急剧变小，样本单元面积大于100 m²以后，随着样本单元面积的增加，变动系数缓慢增加，增加的幅度越来越小，渐渐趋于一个很小的常数; 3)沙枣总体的模拟研究中，变动系数随着样本单元面积的增加也呈递减趋势，样本单元面积小于200 m²时，变动系数随样本单元面积的增加急剧变小，样本单元大于200 m²以后，随着样本单元面积的增加，变动系数缓慢增加，增加的幅度越来越小，渐渐趋于一个很小的常数。

通过对沙漠边缘稀少、群团状的典型灌木(花棒、柽柳)和小乔木(沙枣)进行自适应群团抽样的模拟抽样研究，提出采用变动系数作为衡量自适应群团抽样适宜样本单元面积大小选取的指标，得到变动系数随着样本单元面积大小增加而递减的规律: 同一抽样总体，当初始样本量相同、单元面积大小不同时，所抽取的单元包含的总体信息也不一致，单元面积越大，所包含的总体信息越多，抽样精度越高，抽样效果越好，因此，随着样本单元面积的增加，变动系数将变小，渐渐趋于一个稳定的常数。然而单元面积越大，所产生的外业调查经费也会越高。因此，对于同一种抽样方法，抽样调查精度与费用往往是相互矛盾的。当抽样单元面积大小增加到一定程度时，会出现一个转折点(或者区间)，在此点(或区间)之前，随着单元面积大小的增加，抽样精度会急剧增加，在这个点(区间)之后，随着抽样单元面积大小的增加，抽样精度增加幅度会很小，甚至趋于零。因此，利用此点(或者区间)，可以找到适宜的抽样单元面积大小。

1)对于分布稀少、群团状的灌木(如花棒、柽柳)，进行自适应群团抽样调查时，其最小的适宜样本单元面积为100 m²，可以采用的适宜单元面积大小区间为100~200 m²。因为在单元面积小于100 m²时，变动系数随着单元面积的增加急剧变小，抽样精度大幅提高，当单元大小变为100 m²以后，变动系数随着单元面积的增加缓慢变小，抽样精度提高的幅度急剧变小，慢慢趋于一个很小的常数，而此时抽样调查的成本会随着单元大小的增加而大幅增加。

2)对于分布稀少、群团状的小乔木(如沙枣)，进行自适应群团抽样调查时，其最小的适宜样本单元面积为200 m²，可以采用的适宜单元面积大小区间为200~300 m²。因为在单元面积小于200 m²时，变动系数随着单元面积的增加急剧变小，抽样精度大幅提高，当单元面积大于200 m²以后，变动系数随着单元面积的增加缓慢变小，抽样精度提高的幅度急剧变小，慢慢趋于一个很小的常数，而此时抽样调查的成本会随着单元面积的增加而大幅增加。

3)5种不同初始样本的结果趋于一致，说明模拟试验结果适用性强。

分析所得的结果能为稀少、群团状植被野外实际调查提供重要的理论依据，利用所得研究结果既能保证抽样估计精度，又能节省野外调查成本。

本文中的沙枣是人工林，但是在研究区中其分布是稀少、群团状的，因此，在一定程度上能代表沙漠边缘稀少、群团状的小乔木;但沙枣并不一定是沙漠边缘典型分布稀少、群团状的小乔木。然而，从抽样的角度来看，只要是稀少、群团状分布的植被，即可选择自适应群团抽样。因此，选人工沙枣作为研究对象，其研究结论依然是可靠的，研究结果是有理论和实际参考价值的。

影响适宜单元面积大小的还有抽样调查成本，因此，建议在调查经费充足的情况下，选取的外业调查单元面积可以稍大于前面所提的适宜面积。在外业调查经费不是很充足的情况下，建议选用本文所提的适宜面积。

样本单元面积变化的同时，总体网络的结构也会发生变化，而总体的网络结构在一定程度上会影响自适应群团抽样的效率(Smith et al.，1995; Brown，1996; Thompson et al.，1996; Christman，1996a; 1996b)，这也是一个值得进一步研究的方向。