文章信息
- 张雄清, 张建国, 段爱国
- Zhang Xiongqing, Zhang Jianguo, Duan Aiguo
- 基于贝叶斯法估计杉木人工林树高生长模型
- Tree-Height Growth Model for Chinese Fir Plantation Based on Bayesian Method
- 林业科学, 2014, 50(3): 69-75
- Scientia Silvae Sinicae, 2014, 50(3): 69-75.
- DOI: 10.11707/j.1001-7488.20140310
-
文章历史
- 收稿日期:2013-05-21
- 修回日期:2013-08-29
-
作者相关文章
杉木(Cunninghamia lanceolata)是我国亚热带地区特有的优良用材树种,也是我国南方主要的造林树种。第7次全国森林资源清查表明,全国杉木人工林面积为853.86万hm2,占全国造林面积的21.35%,在我国森林资源中占有重要的地位。杉木人工林树高生长模型是杉木林分生长与收获模型系统中一个重要的组成部分。树高不仅能反映出立地质量的好坏,而且也是林分蓄积量乃至生物量计算的一个重要因子。杉木人工林树高生长模型的研究,可为林业工作者编制杉木人工林各类经营数表、揭示杉木人工林树高生长发育规律提供重要的参考依据。Chave等(2005)发现在估计热带森林生物量时,影响因素按照重要性分别为胸径、木材密度、树高和森林类型,并且在热带森林生物量模型中引入树高使得生物量的估计误差从19.2%减到12.5%。因此,精确的杉木人工林树高生长模型对杉木人工林生物量的估计及杉木人工林经营管理决策非常重要。由于树木生长速度随树龄的增加而变化,即缓慢—旺盛—缓慢—停止,树木生长曲线有拐点,因此反映总生长量变化过程的曲线是一个"S"型曲线生长方程。常用的理论生长方程有Richards方程、Logistic方程、单分子方程、Gompertz方程等。Richards生长方程适应性强、准确性高,方程中的各参数都有一定的生物学意义,在国内外生长收获预估中得到广泛应用(Pienaar et al.,1984; 张建国等,2003)。魏晓惠等(2012)基于Richards方程建立了杉木人工林树高生长模型,并通过传统推断法(最小二乘法)估计模型参数,研究发现Richards参数的估计值符合杉木人工林的生长规律,且树高生长的模拟精度比较高。但是,利用传统的推断法很难对参数估计的不确定性和预测值的可靠性进行评价(Li et al.,2012)。
近些年,根据文献报道,贝叶斯法(Bayesian method)是评价模型不确定性的一个很好的方法,已经在环境、生态、医疗、水文等研究领域得到了广泛应用(Lamon et al.,1998; Clyde,1999; Ellison,2004; 李向阳,2005)。而且贝叶斯法综合利用了先验信息和样本信息,先验信息是在进行统计推断时不可缺少的一个因素,可以来自历史文献资料或者主观信念,这在林业研究工作中是很重要的。如在森林资源连续调查中,每一次调查分析结果都是下一次调查分析的最合理的先验信息。在林业中,贝叶斯法也有一定的研究,如地上生物量模型(Zapata-Cuartas et al.,2012; Zhang et al.,2013)、直径分布模型(Bullock et al.,2007)、直径生长模型(Clark et al.,2007)等,但是,贝叶斯方法在杉木人工林树高生长模型中的研究未见报道。本文以江西杉木人工林为研究对象,以Richards方程为基础模型,利用贝叶斯法估计杉木人工林树高生长模型,并与传统法(非线性最小二乘法)进行比较分析,为分析杉木人工林树高生长模型预测结果的可靠性提供了理论依据。
1 试验地概况及数据整理试验地位于江西省分宜县大岗山年株林场场部后山,属于罗霄山脉北端的武功山支脉,114°30'—114°45'E,27°30'—27°50'N。年株林场场部后山海拔250 m,低山,母岩为砂页岩,年平均气温16.8 ℃,降雨量1 656 mm,年蒸发量1 503 mm,属南亚热带季风气候区。
该试验林使用1年生苗木于1981年造林,采用随机区组试验设计,5个密度: A密度(2 m×3 m)、B密度(2 m×1.5 m)、C密度(2 m×1 m)、D密度(1 m×1.5 m)、E密度(1 m×1 m),每个密度3次重复,总共15个样地,每个样地面积600 m2。1989年前逐年调查,1989年后隔年调查。样地内每株树进行编号,对样地内林木进行每木检尺。本研究数据来源于中国林业科学研究院林业研究所森林培育室1985—1997年的调查数据。到1997年时,A密度林分的平均保留密度为1 661株·hm-2,B密度林分的平均保留密度为3 305株·hm-2,C密度林分的平均保留密度为4 833株·hm-2,D密度林分的平均保留密度为6 255株·hm-2,E密度林分的平均保留密度为9 494株·hm-2。在A密度林分中,1985—1989年样地内所有树高都进行测量。由于随着树高的生长,调查难度增大,1989后选取50株树测量树高。在其他4个密度林分中,都是随机选取50株树测量树高。各林分内的树高统计量见表 1。
|
|
由于林分密度对树高生长的影响比较复杂,不同的情况下得出结论的不同,因此,本研究分为2个步骤: 1)基于Richards方程根据5个不同密度的林分分别建立杉木人工林树高生长模型(3个重复,共计15个方程),并通过方差分析比较不同密度林分树高生长模型各参数的显著性差异; 2)若差异显著,则针对不同的模型,基于贝叶斯估计和传统估计进行比较,若差异不显著,则对所有的密度林分建立树高生长模型,并对贝叶斯估计和传统估计法进行比较分析。其中,在贝叶斯估计中,分别利用有信息先验分布和无信息先验分布对杉木人工林树高生长模型进行估计。
2.1 树高生长模型的建立Richards生长方程由于具有广泛的适应性、合理解析性和良好的拟合性,故此方程是近代林业模型中应用最为广泛的一种生长曲线方程(段爱国等,2003)。Richards生长方程的形式为:
| $ H = a{[1 - \exp(- bt)]^c}. $ | (1) |
贝叶斯法是基于贝叶斯定理而发展起来用于系统地阐述和解决统计问题的方法。一个完全的贝叶斯分析包括数据分析、概率模型的构造、先验信息(先验分布)和效应函数的假设以及最后的决策(Lindley,2004)。贝叶斯推断的基本方法是将未知参数的先验信息与样本信息结合,再根据贝叶斯定理得出后验信息,然后根据后验信息去推断未知参数的分布(茆诗松等,2004)。令y=(y1,y2,y3,…)为数据向量,θ=(θ1,θ2,θ3,…)为参数向量,则根据贝叶斯理论,其基本公式为:
| $ p(y,\theta)= p(y|\theta)p(\theta)= p(\theta |y)p(y). $ | (2) |
| $ p(\theta |y)= \frac{{p(y|\theta)p(\theta)}}{{p(y)}}. $ | (3) |
其中对于连续型θ,p(y)=Eθ[p(y|θ)]=∫p(y|θ)p(θ)d(θ)。贝叶斯法中,在给定样本y下θ的条件分布p(θ|y)就是我们所要求得参数的后验分布,p(y|θ)是在给定θ下y的似然函数,p(θ)是θ的先验分布。
2.3 先验分布先验分布的选择在贝叶斯法中是非常重要的(Gelman et al.,2004)。在上述的杉木人工林生长方程中,需要为参数a,b,c选择合适的先验分布。许多学者选择利用无信息先验分布(non-informative prior),该信息可以忽略不计,而且对参数估计的影响不大。对于无信息先验分布,一般选择均值为0、方差足够大的能够覆盖整个数据范围的正态分布(Ellison,2004)。当然也可以选择有信息先验分布(informative prior)作为贝叶斯法中的先验分布,这些信息可以来自历史文献资料或者主观信念。本研究中,Richards方程中3个参数的无信息先验分布分别为 a~N (0,1 000),b~N (0,1 000),c~N (0,1 000),有信息先验分布则可以根据前面所计算的15个方程的参数估计值得到。
对于贝叶斯参数估计,本研究利用WinBUGS软件(Spiegelhalter et al.,2003)完成。该软件通过吉布斯抽样算法(Gibbs sampling)(Chib et al.,1995)估计参数。本研究还通过R2WinBUGS(Sturtz et al.,2005)连接R软件和WinBUGS软件完成数据的输入和输出以及图形的生成。对于方差分析和传统推断法估计参数,在SAS软件中完成。在进行贝叶斯估计时,为了保证迭代收敛和得到稳定的参数后验概率值,迭代次数设为10万次,并去掉前面的5 000次退火(burn-in)迭代。
3 模型评价在传统方法中,一般采用均方根误差(RMSE)作为模型的拟合统计量指标:
| $ {\text{RMSE}} = \sqrt {\sum {{{({y_i} - {{\hat y}_i})}^2}/n} } . $ | (4) |
对于贝叶斯模型,DIC统计量是个非常好的拟合评价指标(Spiegelhalter et al.,2002)。与RMSE值一样,DIC值越小,说明模型拟合越好:
| $ {\text{DIC}} = {D_{bar}} + m. $ | (5) |
在15个林分中分别利用Richards方程建立单木树高生长模型,其参数估计值见表 2。根据方差分析,发现表 2中a,b,c 3个参数估计值在5个密度林分中差异不显著(表 3)。因此,在本研究中,林分初植密度对树高生长模型的影响不显著。
|
|
|
|
根据上述结果发现,林分初植密度对杉木人工林树高生长模型影响不显著。根据贝叶斯法估计杉木人工林树高生长模型参数,其参数的后验概率分布见图 1。根据图 1,可以发现杉木人工林树高生长模型的参数是随机变量,服从一定的分布,这就更好地解释了树高生长模型的不确定性。
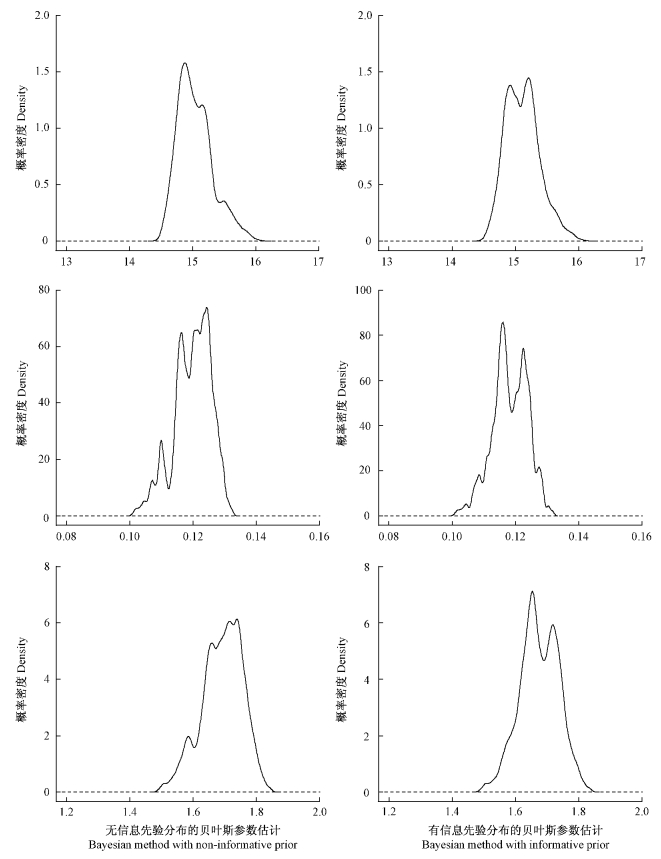 |
图 1 杉木人工林树高生长模型的参数后验概率分布
Fig. 1 Posterior density curves of 3 parameters based on Bayesian estimate
|
表 4为基于5个密度所有林分内的林木树高数据建立的杉木人工林树高生长模型并分别通过传统法(非线性最小二乘法)和贝叶斯法估计的模型参数。由表 4可以发现,贝叶斯法的参数估计置信区间比传统法估计的都要窄,因此基于贝叶斯法估计的参数比较稳定、可靠,而且利用有信息先验分布估计的参数区间比无信息先验分布的区间更窄、更稳定。通过比较RMSE值,贝叶斯法要略好于传统法;而且对比DIC值发现,有信息先验分布的贝叶斯法拟合效果更好(表 4)。
|
|
根据图 2可以发现,基于贝叶斯法预测杉木人工林树高,预测值的置信区间比传统法的置信区间要小得多。这是因为贝叶斯法综合利用了样本信息和先验分布信息,而且在贝叶斯法中,参数是随机变量,使得贝叶斯法的预测值更为可靠、稳定。
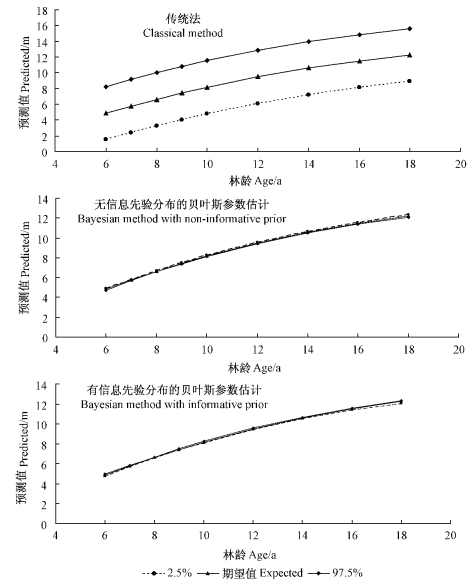 |
图 2 杉木人工林树高生长模型预测值的95%置信区间
Fig. 2 95% confidence intervals of predicted height growth for Chinese fir plantation
|
林分密度对树高的影响目前结论各不一样。Tong等(2005)研究发现相同立地条件下北美短叶松(Pinus banksiana)间伐林分内的平均树高显著大于不间伐的林分。童书振等(2002)和揭建林等(2007)认为林分的优势高和平均高随林分密度的增加而递减。也有个别研究(Knowe et al.,1996)发现在幼龄林期,红桤木(Alnus rubra)的树高生长与林分密度正相关。但更多的研究(Hummel,2000; Li et al.,2007; Zhang et al.,2007)表明,林分密度对树高的影响不显著。在本研究中,通过5个不同密度杉木人工林林分分别建立树高生长模型,并通过方差分析密度对杉木人工林树高生长的影响,结果表明密度对树高生长的影响不显著,与大部分研究结论一致。
本研究分别利用贝叶斯法和传统法(非线性最小二乘法)估计杉木人工林树高生长模型。研究发现,通过贝叶斯法估计树高生长模型,虽然预测精度与传统法相当,但是其预测值的可靠性、稳定性更好。这是因为在样本量比较大时,传统法和贝叶斯法的模拟精度比较接近,当样本量比较小时,贝叶斯法的模拟精度要高于传统法(Zapata-Cuartas et al.,2012)。贝叶斯法在统计推断的研究方面比传统法有很大的优势,主要表现在: 贝叶斯法综合利用了先验信息和样本信息,先验信息(分布)是在进行统计推断时不可缺少的一个因素,可以来自历史资料(文献)或者主观信念,而传统法仅利用了样本信息(Ellison,2004; McCarthy,2007); 贝叶斯法把样本和参数看作是随机变量,而传统法把未知参数估计值看作固定值(Ellison,2004; Li et al.,2012); 贝叶斯法并没有对参数或模型的构造加以限制,而传统法一般假设服从正态分布(Davidian et al.,1995)。
总之,利用贝叶斯法估计杉木人工林树高生长模型,预测效果更可靠、更稳定,今后应该加强贝叶斯法在林业模型中的应用研究。当然,也可以在杉木人工林树高生长模型中加入立地质量、环境变量等一些因素,建立分层贝叶斯模型,使得先验分布更精确,进而提高杉木人工林树高生长模型的精度。
| [1] |
段爱国, 张建国, 童书振. 2003. 6种生长方程在杉木人工林林分胸径结构上的应用. 林业科学研究, 16(4): 423-429.( 1) 1)
|
| [2] |
揭建林, 骆昱春, 龙 蔚, 等. 2007. 南岭山地杉木人工林密度试验研究. 江西农业大学学报, 29 (2): 203-208.( 1) 1)
|
| [3] |
李向阳. 2005. 水文模型参数优选及不确定性分析方法研究. 大连: 大连理工大学博士学位论文.( 1) 1)
|
| [4] |
茆诗松,王静龙,濮晓龙. 2004. 高等数理统计. 北京: 高等教育出版社.( 1) 1)
|
| [5] |
童书振, 盛炜彤. 2002. 杉木林分密度效应研究. 林业科学研究, 15(1): 66-75.( 1) 1)
|
| [6] |
魏晓惠, 孙玉军, 马 炜. 2012. 基于Richards方程的杉木树高生长模型. 浙江农林大学学报, 29(5): 661-666.( 1) 1)
|
| [7] |
张建国, 段爱国. 2003. 理论生长方程对杉木人工林林分胸径结构的模拟研究. 林业科学, 39(6): 55-61.( 1) 1)
|
| [8] |
Bullock B P, Boone E L. 2007. Deriving tree diameter distributions using Bayesian model averaging. Forest Ecology and Management, 242 (2/3): 127-132.( 1) 1)
|
| [9] |
Chave J, Andalo C, Brown S, et al. 2005. Tree allometry and improved estimation of carbon stocks and balance in tropical forests. Oecologia, 145(1): 87-99.( 1) 1)
|
| [10] |
Chib S, Greenberg E. 1995. Understanding the Metropolis-Hastings algorithm. The American Statistician, 49(4): 327-335.( 1) 1)
|
| [11] |
Clark J S, Wolosin M, Dietze M, et al. 2007. Tree growth inference and prediction from diameter censuses and ring widths. Ecological Applications, 17(7): 1942-1953.( 1) 1)
|
| [12] |
Clyde M. 1999. Model uncertainty and health effect studies for particulate matter. Technical Report Series, NRCSE-TRS No.027.( 1) 1)
|
| [13] |
Davidian M, Giltinan D M. 1995. Nonlinear models for repeated measurement data. New York: Chapman and Hall.( 1) 1)
|
| [14] |
Ellison A M. 2004. Bayesian inference in ecology. Ecology Letters, 7(6): 509-520.( 3) 3)
|
| [15] |
Gelman A, Carlin J B, Stern H S. 2004.Bayesian data analysis.2nd ed.USA:Chapman and Hall/CRC.( 1) 1)
|
| [16] |
Hummel S. 2000. Height, diameter and crown dimensions of Cordia alliodora associated with tree density. Forest Ecology and Management, 127(1): 31-40.( 1) 1)
|
| [17] |
Knowe S A, Hibb D E. 1996. Stand structure and dynamics of young red alder as affected by planting density. Forest Ecology and Management, 82(1/3): 69-85.( 1) 1)
|
| [18] |
Lamon E C, Clyde M. 1998. Accounting for model uncertainty in prediction of chlorophylla in Lake Okeechobee. ISDS Discussion Paper, 98-42.( 1) 1)
|
| [19] |
Li R, Stewart B, Weiskittel A. 2012. A Bayesian approach for modelling non-linear longitudinal/hierarchical data with random effects in forestry. Forestry, 85(1): 17-25.( 2) 2)
|
| [20] |
Li Y, Turnblom E, Briggs D. 2007. Effects of density control and fertilization on growth and yield of young Douglas-fir plantations in the Pacific Northwest. Canadian Journal of Forest Research, 37 (2): 449-461.( 1) 1)
|
| [21] |
Lindley D V. 2004. Bayesian thoughts. Significance, 1(2): 73-75.( 1) 1)
|
| [22] |
McCarthy M A. 2007. Bayesian methods for ecology. Cambridge University Press, Cambridge, UK.( 1) 1)
|
| [23] |
Pienaar L V, Shiver B D.1984. An analysis and models of basal area growth in 45-year-old unthinned and thinned slash pine plantation plots. Forest Science, 30(4): 933-942.( 1) 1)
|
| [24] |
Spiegelhalter D J, Best N G, Carlin B P, et al. 2002. Bayesian measures of model complexity and fit. Journal of Royal Statistical Society: Series B, 64(4): 583-639.( 1) 1)
|
| [25] |
Spiegelhalter D J, Thomas A, Best N, et al. 2003. WinBUGS User Manual. http://www.mrc-bsu.cam.ac.uk/bugs (accessed on 2 October, 2011).( 1) 1)
|
| [26] |
Sturtz S, Ligges U, Gelman A. 2005. R2WinBUGS: a package for running WinBUGS from R. Journal of Statistic Software, 12(3): 1-16.( 1) 1)
|
| [27] |
Tong Q, Zhang S, Thompson M. 2005. Evaluation of growth response, stand value and financial return for pre-commercially thinned jack pine stands in Northwestern Ontario. Forest Ecology and Management, 209 (3): 225-235.( 1) 1)
|
| [28] |
Zapata-Cuartas M, Sierra C A, Alleman L. 2012. Probability distribution of allometric coefficients and Bayesian estimation of aboveground tree biomass. Forest Ecology and Management, 277: 173-179.( 1) 1)
|
| [29] |
Zhang J, Oliver W W, Ritchie M W. 2007. Effects of stand densities on stand dynamics in white fir (Abies concolor) forests in northeast California, USA. Forest Ecology and Management, 244(1/3): 50-59.( 1) 1)
|
| [30] |
Zhang X, Duan A, Zhang J. 2013. Tree biomass estimation of Chinese fir (Cunninghamia lanceolata) based on Bayesian method. PLOS ONE, 8(11): 1-7.( 1) 1)
|
 2014, Vol. 50
2014, Vol. 50

