文章信息
- 罗勇锋, 李羲, 李贤军, 陈红斌, 柴媛
- Luo Yongfeng, Li Xi, Li Xianjun, Chen Hongbin, Chai Yuan
- 木材微波预处理圆柱形谐振腔理论模拟与设计
- Mathematical Simulation and Design of Cylindrical Cavity of Microwave Pretreatment Equipment Used for Wood Modification
- 林业科学, 2014, 50(3): 117-122
- Scientia Silvae Sinicae, 2014, 50(3): 117-122.
- DOI: 10.11707/j.1001-7488.20140316
-
文章历史
- 收稿日期:2013-06-13
- 修回日期:2013-08-02
-
作者相关文章
2. 中南林业科技大学材料科学与工程学院 长沙 410004
2. School of Material Science and Engineering, Central South University of Forestry and Technology Changsha 410004
微波预处理是20世纪末始于澳大利亚的木材改性新技术,其基本原理是利用微波对湿木材进行瞬时处理,使木材内部水分在短时间内获得足够多的能量,产生相变和气体热压效应,在蒸汽膨胀动力带动下,破坏木材内部微观构造,形成新的流体通道,提高木材后期干燥与浸注改性处理效率,甚至将木材拆解为具有松散结构的膨化木材,再将其与其他材料复合,制备出功能性木质复合材料。澳大利亚Torgovnikov和Vinden等学者(Torgovnikov et al.,2000; 2006; 2009; 2010; Vinden et al.,,2011; Mekhtiev et al.,2004; Przewloka et al.,2007; Harris et al.,2008; Krisdianto et al.,2010)的研究表明: 经微波预处理,木材体积可增大13.4%,防腐剂渗透量可增加10~14倍,木材弹性模量降低12%~17%,干燥合格率提高5%以上; 能制备具有高渗透性、低密度、隔音效果好的膨化木材——Torgvin和具有高强度、高表面硬度的新型木质复合材料——Vintrog。这一创新性研究为速生人工林木材的高附加值利用开辟了一条崭新道路,显示出了潜在的巨大应用价值。在国内,近年来中国林业科学研究院木材所、东北林业大学、中南林业科技大学等单位也开展了木材微波预处理技术的探索性研究,取得了初步成果(吕悦孝等,2001; 王喜明等,2002; 赵荣军等,2003; 江涛等,2006; 周志芳等,2007; 周永东等,2009; 2011; Li et al.,2005; 2010; 王婧,2010; 李贤军等,2012)。但与此同时,国内外的研究也发现采用微波对木材进行预处理时还存在诸多问题,其中最主要的问题之一是木材微波改性处理不均匀。要获得均匀的微波改性处理材,笔者认为最核心的工作是研制出场强分布均匀的微波谐振腔及其微波预处理设备。基于此,本文将在构建微波预处理过程中木材内电磁场分布和热质迁移模型(Hansson et al.,2008; Marra et al.,2010)的基础上,通过数字模拟方法,研究微波馈入方式及谐振腔半径对木材内温度分布均匀性和微波能量利用效率的影响规律,获得优化的微波谐振腔型,以期为木材微波预处理设备的研制和木材微波预处理技术后续研究提供参考和借鉴。
1 模型构建在理论模拟微波加热过程中,分析置于多馈入口圆柱形谐振腔内的木材中电磁场和温度场分布情况时,为简化分析和理论计算,先对模型进行以下假设: 1)木材初始温度和含水率分布均匀; 2)微波加热过程中木材体积保持不变; 3)圆柱形木材与谐振腔共轴; 4)木材表面和空气之间的热量交换满足对流和传热边界条件。
1.1 电磁场与微波能量分布模型根据麦克斯韦方程组,微波加热过程中木材内的电磁场分布满足如下方程:
| $ \nabla \times \vec E{\rm{ = }} - \frac{{\partial \vec B}}{{\partial t}}; $ | (1) |
| $ \nabla \times \vec H{\rm{ = }}\vec J + \frac{{\partial \vec D}}{{\partial t}}; $ | (2) |
| $ \nabla \cdot \vec B{\rm{ = }}0; $ | (3) |
| $ \nabla \cdot \vec D{\rm{ = }}{\rho _c} $。 | (4) |
式中:$\vec E$为电场强度,$\vec H$为磁场强度,$\vec B$为磁感应强度,$\vec D$为电位移,$\vec J$为电流密度,ρc为自由电荷密度; 其中$\vec J = \sigma \vec E,\vec D = \varepsilon \vec E,\vec B = \mu \vec H$,σ为电导率,ε为介电常数,μ为磁导率。根据方程(1)~(4)可计算出木材内部电磁场的分布情况。
在本研究中,微波激励源采用时谐电磁场$\vec E$10膜,即$\vec E = \vec E\left( {\vec r} \right){e^{ - i\omega t}},\vec H = \vec H\left( {\vec r} \right){e^{ - i\omega t}}$,$\vec B$和$\vec D$可以表示成$\vec E$和$\vec H$的函数:
| $ \nabla \times \vec E\left( {\vec r} \right) = i\omega \mu \vec H\left( {\vec r} \right); $ | (5) |
| $ \nabla \times \vec H\left( {\vec r} \right) = \left( {\sigma - i\omega \varepsilon } \right)\vec E\left( {\vec r} \right) = - i\omega {\varepsilon ^*}\vec E\left( {\vec r} \right) $。 | (6) |
式中: i为虚数单位,ω为角频率,$\vec r$为空间位置矢量,ε*为复介电常数,可以表示成ε*=ε'+iε″。
由式(5)和(6)可得(Ayappa,1997):
| $ \nabla \left( {\vec E \cdot \frac{{\nabla {\varepsilon ^*}}}{{{\varepsilon ^*}}}} \right) + {\nabla ^2}\vec E + {k^2}\vec E = 0 $。 | (7) |
通过求解式(7)可以得到木材中的电场分布。在本研究中假设沿电场方向木材介电常数为恒定值,所以式(7)的第1项为零,可简化为:
| $ {\nabla ^2}\vec E + {k^2}\vec E = 0 $。 | (8) |
式中: k取决于木材介电性质,其表达式为:
| $ k = \alpha + i\beta ; $ | (9) |
| $ \alpha = \frac{{2\pi f}}{c}\sqrt {\frac{{\varepsilon '\left( {\sqrt {1 + {{\tan }^2}\delta } + 1} \right)}}{2}} ; $ | (10) |
| $ \beta = \frac{{2\pi f}}{c}\sqrt {\frac{{\varepsilon '\left( {\sqrt {1 + {{\tan }^2}\delta } - 1} \right)}}{2}} $。 | (11) |
式中: f为微波辐射频率; tanδ为木材损耗因子,其值可以通过下式计算:
| $ \tan \delta = \frac{{\varepsilon ''}}{{\varepsilon '}} $。 | (12) |
模拟木材中的电场分布时,式(8)由下列边界条件求解:
| $ n \times \left[ {{{\vec E}_1}\left( {\vec r} \right) - {{\vec E}_2}\left( {\vec r} \right)} \right] = 0; $ | (13) |
| $ n \times \left[ {{{\vec H}_1}\left( {\vec r} \right) - {{\vec H}_2}\left( {\vec r} \right)} \right] = 0 $。 | (14) |
式(13),(14)中的下标1代表空气,下标2代表木材。式(14)也可以通过下
式表示成电场强度的函数:
| $ \frac{{\partial \vec E\left( {\vec r} \right)}}{{\partial r}} = i{\mu _0}\omega \vec H\left( {\vec r} \right) $。 | (15) |
式(8)的解由两相反方向传播的波动函数构成:
| $ E = {A_1}{e^{ikr}} + {B_1}{e^{ - ikr}} $。 | (16) |
式中: A1和B1由边界条件(13)和(14)确定。根据求解出的木材内电场,可以应用坡印廷定理求出木材内任一位置的电磁场能量密度:
| $ Q = \frac{1}{2}\omega {\varepsilon _0}\varepsilon ''\vec E \cdot {\vec E^*} $。 | (17) |
式中: ε0为真空介电常数,${\vec E^*}$为电场复共轭。
1.2 热迁移模型微波预处理过程中,木材内部的微观热量平衡可以由下式描述(Ayappa,1997):
| $ \rho {C_p}\frac{{\partial T}}{{\partial t}} = \nabla \cdot \left( {{k_T}\nabla T} \right) + Q $。 | (18) |
式中: ρ,CP和kT分别为木材密度、比热和热导率; Q为木材内的电磁场能量密度。
方程(18)的边界条件为:
| $ t = 0,T = {T_{ini}},0 \le r \le R; $ | (19) |
| \[\begin{array}{*{20}{l}} {t > 0, - {k_T}\frac{{\partial T}}{{\partial r}} = h\left( {T - {T_a}} \right) + }\\ {{L_{vap}}k'm\left( {{C_{w,s}} - {C_{equi}}} \right),r = R} \end{array}\] | (20) |
式中: R为圆柱形木材的半径; h为木材内的热传导系数; Ta和Tini为空气、木材初始温度; Lvap为水的汽化热; k'm为水分交换系数; Cw,s为木材表层含水率; Cequi为空气平衡含水率。
1.3 质迁移模型微波预处理过程中,木材内部的水分迁移可以由下式描述(Marra et al.,2010):
| $ \frac{{\partial {C_w}}}{{\partial t}} = \nabla \left( {{D_w}\nabla {C_w}} \right) $。 | (21) |
式中: Dw为木材水分扩散系数。
方程(21)的边界条件为:
| $ t = 0,{C_w} = {C_{w,ini}},0 \le r \le R; $ | (22) |
| $ t > 0, - {D_w}\frac{{\partial C}}{{\partial x}} = k{'_m}\left( {{C_{w,s}} - {C_{equi}}} \right),r = R $。 | (23) |
根据上述建立的木材电磁场、微波能量及热质迁移模型,结合给定的参数,运用有限元分析软件(Comsol Multiphysics)就可以模拟出微波预处理过程中木材内的电磁场和温度分布规律。在本文中,当研究微波馈入方式对木材内温度分布均匀性和微波能量利用效率的影响时,微波工作频率为915 MHz,圆柱形谐振腔的半径为0.247 65 m(波导的长度),圆柱形谐振腔的长度为0.5 m; 微波激励源采用多口同相位微波馈入,多口馈入的微波总功率为40 kW,功率平均分配到各馈入口; 各馈入口沿着圆柱形谐振腔的圆周均匀分布,馈入口波导采用BJ9标准型波导(长为0.247 65 m,宽为0.123 82 m,高为0.082 16 m); 木材初始含水率取60%,直径为0.3 m,长度为0.75 m,相对介电常数为7.40,介电损耗因素为1.42,初始温度为25 ℃,密度为570 kg·m-3,其导热系数和比热由下式计算:
λ=0.23[1-0.72×(25-T)/100]W·m-1℃-1;C=2 650×(1+T/100)0.2J·kg-1℃-1。
当研究谐振腔半径对木材内温度分布均匀性和微波能量利用效率的影响时,除了微波谐振腔半径变化外,上述其他参数保持不变。
2.1 馈入方式对木材内温度分布均匀性和微波能量利用效率的影响图 1表示微波馈入方式对木材内温度空间分布的影响规律。从图中可以看出: 微波馈入口处木材内的温度最高,沿着木材纵向,距离微波馈入口中央横截面越远,木材内部的温度越低; 以微波馈入口处的中央横截面为界,微波馈入口两侧木材内截面上的温度分布呈对称形式,各截面的温度分布模式也基本一致。
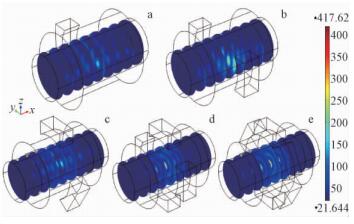 |
图 1 不同馈入方式木材内温度空间分布
Fig. 1 The temperature distribution within wood heated by microwave with different radiation methods
|
由于采用不同微波馈入方式加热木材时,微波馈入口中央横截面的温度最高,且沿着木材纵向,木材内各横截面的温度分布模式基本一致,因此,可将图 1中微波馈入口中央横截面的温度分布图单独提取出来(图 2),用以研究微波馈入方式对木材内横截面上温度分布均匀性的影响规律。从图 2可以明显看出: 1)对于单微波口馈入(图 2a),木材横截面上温度呈不对称分布,高温区在微波馈入口附近,远离微波馈入口,木材内温度低,木材内温度分布不均匀,对微波木材改性处理不利; 2)对于对称分布的双微波口馈入(图 2b),木材横截面上的温度分布沿Y轴和Z轴方向呈对称分布,但木材横截面上温度分布的均匀性较差; 3)对于沿圆周均匀分布的三微波口馈入(图 2c),木材横截面上的较高温区域出现在木材轴心附近区域,温度分布基本呈轴对称形式,温度分布比较均匀,这是因为在该微波频率、谐振腔与木材半径的情况下,微波馈入时在木材表面、1/2半径和木材中心处形成3个高温区域,三微波口馈入时木材中心处的温度(3个方向叠加形成)与1/2半径处基本相等,导致整体温度分布较均匀; 4)对于沿圆周均匀分布的四微波口和六微波口馈入(图 2d和图 2e),温度分布虽也呈对称分布,但高温区集中在木材轴心,木材轴心区域与周边区域的温差过大,与三口馈入相比,木材横截面上的温度分布不均匀,不利于木材的微波改性处理。出现这种现象的根本原因在微波衰减和微波干涉2个方面,即在微波传输方向上微波场强度逐渐降低,同时微波从波导馈入口进入谐振腔后会发生干涉现象,不同的微波馈入方式使得微波在谐振腔内发生衰减和干涉的情况不一致,直接导致了木材内温度分布模式的显著区别。
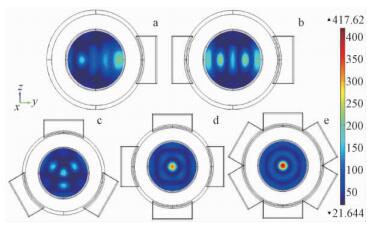 |
图 2 不同馈入方式木材内中央截面温度分布
Fig. 2 The central section temperature distribution within wood heated by microwave with different radiation methods
|
为定量描述微波馈入方式对木材中央横截面上温度分布均匀性的影响,对该截面温度分布的变异系数进行分析(图 3)。从图 3可以看出,当当采用三微波口馈入方式加热方式加热时,木材横截面上的温度变异系数最小,温度分布最均匀,其次为四微波口馈入; 而当采用二微波口馈入方式加热时,木材横截面上温度分布的均匀性最差; 该定量分析结果与图 2中直观呈现的定性结果完全一致。除研究微波馈入方式对木材内温度分布均匀性的影响外,本文还探讨了微波辐射方式对微波能量利用效率的影响规律。从图 3还可以看出,采用三微波口馈入方式加热时,微波能量利用效率最高,达到87.48%; 而采用四微波口馈入时,微波能量利用效率最低,降至71.79%。当采用一、二、六微波口馈入时,其微波能量利用效率分别为81.81%,81.72%,84.93%。这说明在四微波口馈入时,在谐振腔内微波场发生了严重的干涉现象,形成了"驻波",使得有较大部分的微波能量被"空耗"。
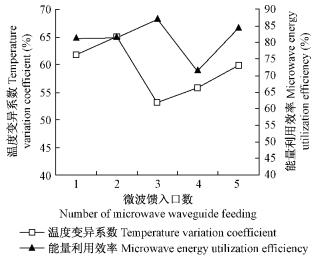 |
图 3 馈入方式对温度变异系数和能量利用效率的影响
Fig. 3 The effect of microwave radiation methods on the temperature variation coefficient and microwave energy utilization efficiency
|
综合考虑微波馈入方式对木材横截面温度分布均匀性和微波能量利用数率2方面的影响因素,可以明显看出,采用三微波口馈入方式加热木材时,木材横截面上的温度分布最均匀,微波能量利用效率最高。因此,在设计微波预处理装置对原木进行改性处理时,最好采用三微波口馈入方式的谐振腔。
2.2 谐振腔半径对木材内温度分布均匀性和微波能量利用效率的影响在保持其他参数不变的情况下,为研究谐振腔半径对木材内温度分布均匀性和微波能量利用效率的影响规律,本文模拟了三微波口馈入谐振腔半径0.173 355~0.297 18 m间每隔0.1w时(w为波导宽度0.247 65 m)木材内中央横截面的温度分布情况(图 4、图 5)。从图 4和图 5可以看出,随着谐振腔半径的增加,木材中央横截面上的温度变异系数整体呈现出先减小后增加的变化趋势; 当谐振腔半径介于0.198(图 4c)~0.223 m(图 4g)时,木材横截面上的温度分布比较均匀,温度变异系数小; 当谐振腔的直径小于0.198 m或大于0.248 m时,木材横截面上的温度分布均匀性较差,温度变异系数较大。这说明采用微波对圆柱形木材进行改性预处理时,木材的直径与谐振腔的直径需要匹配,当原木的直径太大(与谐振腔内壁的间隙过小)或者太小(与谐振腔内壁的间隙过大)时,木材横截面上温度分布的均匀性都会降低。
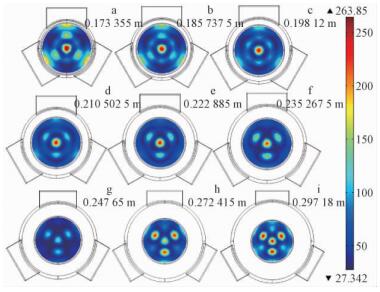 |
图 4 不同谐振腔半径木材内中央截面的温度分布
Fig. 4 The central section temperature distribution within wood heated by microwave with different resonant cavity dimension
|
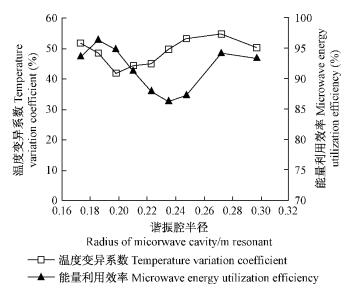 |
图 5 谐振腔半径对温度变异系数和能量利用效率的影响
Fig. 5 The effect of the radius for the microwave resonant cavity on the temperature variation coefficient and microwave energy utilization efficiency
|
从图 5还可以看出,在原木直径一定的情况下,改变谐振腔的半径,微波能量利用效率也将发生变化,其变化规律与木材横截面内的温度变异系数变化规律基本一致。当谐振腔的半径0.211 m<R<0.272 m时,微波能量利用效率较低,这是由于微波能量利用效率取决于谐振腔半径与波长之间的匹配程度。当谐振腔半径0.211 m<R<0.272 m时,较大部分的微波能量以驻波形式存在于谐振腔与木材间的空腔内,导致进入木材的电磁能减少,从而使得微波能量利用效率降低。
综合考虑微波谐振腔对木材横截面温度分布均匀性和微波能量利用效率2方面的影响因素,可以明显看出,当圆柱形微波谐振腔的半径介于0.186~0.211 m之间时,木材横截面上的温度分布比较均匀,且微波能量利用效率较高(在90%以上)。
3 结论本文基于麦克斯韦电磁场方程和木材传热传质机制,构建了微波预处理过程中木材内电磁场分布及热质迁移模型,采用有限元分析软件(Comsol Multiphysics)模拟了微波馈入方式及谐振腔半径对圆柱形谐振腔中木材内温度分布均匀性和微波能量利用效率的影响规律,获得了优化的微波谐振腔型。结果表明: 1)微波馈入方式和谐振腔半径对木材内温度分布均匀性和微波能量利用效率影响显著; 2)与一、二、四和六微波口馈入相比,采用三微波口馈入方式加热时,木材内横截面上温度分布最均匀,微波能量利用效率最高,达到87.48%; 3)随着微波谐振腔半径的增加,木材内温度变异系数和能量利用效率整体呈现出先减小后增加的变化趋势,优化的谐振腔半径介于0.186~0.211 m之间。
| [1] |
江 涛, 周志芳, 王清文. 2006. 高强度微波辐射对落叶松木材渗透性的影响. 林业科学, 42(11): 87-92( 1) 1)
|
| [2] |
李贤军, 孙伟圣, 周 涛,等. 2012. 微波处理中木材内温度分布的数学模拟. 林业科学, 48(3): 117-121( 1) 1)
|
| [3] |
吕悦孝, 薛振华, 薛利忠. 2001. 微波改性木材的超微观察.内蒙古林业科技, (4): 31-33( 1) 1)
|
| [4] |
王喜明, 薛振华, 石丽慧,等. 2002. 微波改性木材的初步研究.木材工业, 16(6): 16-19( 1) 1)
|
| [5] |
王 婧. 2010. 微波预处理对尾叶桉人工林木材干燥特性的影响. 北京: 中国林业科学研究院硕士学位论文.( 1) 1)
|
| [6] |
赵荣军, 王喜明, 江泽慧, 等. 2003. 桉树人工林微波处理材干燥特性和干燥基准. 哈尔滨:第九次全国木材干燥学术讨论会论文集, 62-69( 1) 1)
|
| [7] |
周志芳, 江 涛, 王清文. 2007. 高强度微波处理对落叶松木材力学性质的影响.东北林业大学学报, 35(2): 7-8( 1) 1)
|
| [8] |
周永东, 傅 峰, 李贤军, 等. 2009. 微波处理对桉木应力及微观构造的影响.北京林业大学学报, 31(2): 146-150( 1) 1)
|
| [9] |
周永东, Torgovinkov G, Vinden P, 等. 2011. 微波预处理加速阔叶树材干燥的技术分析. 木材工业, 25(1): 23-25( 1) 1)
|
| [10] |
Ayappa K G. 1997. Modelling transport processes during microwave heating: a review. Reviews in Chemical Engineering, 13(2): 1-69( 2) 2)
|
| [11] |
Hansson L, Antti L. 2008. Modeling microwave heating and moisture redistribution in wood. Drying Technology, 26(5): 552-559( 1) 1)
|
| [12] |
Harris G A, Torgovnikov G, Vinden P, et al. 2008. Microwave pretreatment of backsawn messmate boards to improve drying quality: Part 1. Drying Technol, 26(5): 579-584( 1) 1)
|
| [13] |
Krisdianto S, Vinden P, Torgovnikov G. 2010. Microwave surface modification of Pinus radiata peeler cores: technical and cost analyses. For Prod J, 60(4): 346-352( 1) 1)
|
| [14] |
Li X J, Zhang B G, Li W J, et al. 2005. Research on the effect of microwave pretreatment on moisture diffusion coefficient in wood. Wood Science and Technology, 39(7): 521-528( 1) 1)
|
| [15] |
Li X J, Zhou Y D, Yan Y L, et al. 2010.A single cell model for pretreatment of wood by microwave explosion. Holzforschung, 64(5): 633-637( 1) 1)
|
| [16] |
Marra F, De Boins M V, Ruocco G. 2010. Combined microwaves and convection heating: a conjugata approach. Journal of Food Engineering, 97(1): 31-39( 2) 2)
|
| [17] |
Mekhtiev M A, Torgovnikov G I. 2004. Method of check analysis of microwave-modified wood. Wood science and Technology, 38(7): 507-519( 1) 1)
|
| [18] |
Przewloka S R, Hann J A, Vinden P. 2007. Assessment of commercial viscosity resins as binders in the wood composite material Vintorg. Holzals Roh-und Werkst stoff, 65(3): 209-214( 1) 1)
|
| [19] |
Torgovnikov G, Vinden P. 2000. New wood based materials TORGVIN and VINTORG. 5th Pacific Rim Bio-Based Composite Symposium, Canberra Australia: December 2000, 756-757( 1) 1)
|
| [20] |
Torgovnikov G, Vinden P. 2006. New 300 kW plant for microwave wood modification. International Microwave Power Institute's 40th Annual Symposium, Boston, Massachusetts, USA, 260-263( 1) 1)
|
| [21] |
Torgovnikov G, Vinden P. 2009. High intensity microwave wood modification for increasing permeability. For Prod J, 59(4): 84-92( 1) 1)
|
| [22] |
Torgovnikov G, Vinden P. 2010. Microwave wood modification technology and its application. For Prod J, 60(2): 173-182( 1) 1)
|
| [23] |
Vinden P, Torgovnikov G, Hann J. 2011. Microwave modification of radiata pine railway sleepers for preservative treatment. Eur J Wood Prod, 69(2): 271-279.( 1) 1)
|
 2014, Vol. 50
2014, Vol. 50

