林业科学  2014, Vol. 50 Issue (3): 1-9   PDF    
DOI: 10.11707/j.1001-7488.20140301
0

文章信息

宋于洋, 李园园, 李明艳
Song Yuyang, Li Yuanyuan, Li Mingyan
基于生态用小波的古尔班通古特沙漠梭梭分布格局的周期性特征
Periodic Characteristics of Distribution Pattern of Haloxylon ammodendron in Gurbantunggut Desert Based on Eco-Used Wavelet
林业科学, 2014, 50(3): 1-9
Scientia Silvae Sinicae, 2014, 50(3): 1-9.
DOI: 10.11707/j.1001-7488.20140301

文章历史

收稿日期：2012-11-15
修回日期：2014-01-20

作者相关文章

宋于洋
李园园
李明艳

引用本文
宋于洋, 李园园, 李明艳. 2014. 基于生态用小波的古尔班通古特沙漠梭梭分布格局的周期性特征[J]. 林业科学, 50(3): 1-9.
Song Yuyang, Li Yuanyuan, Li Mingyan. 2014. Periodic Characteristics of Distribution Pattern of Haloxylon ammodendron in Gurbantunggut Desert Based on Eco-Used Wavelet. Scientia Silvae Sinicae, 50(3): 1-9.  DOI: 10.11707/j.1001-7488.20140301
基于生态用小波的古尔班通古特沙漠梭梭分布格局的周期性特征
宋于洋1, 2, 李园园1, 李明艳1    
1. 石河子大学农学院林学系 石河子 832003;
2. 西北农林科技大学教育部西部环境与生态重点实验室 杨凌 712100
收稿日期：2012-11-15；修回日期：2014-01-20
基金项目：新疆生产建设兵团重点公益林生物多样性保护及生态状况监测项目（兵财企2006.813号）。
摘要：应用Mexican Hat和Morlet生态用小波，研究3个地点、3种沙丘类型梭梭分布格局的波动特征。结果表明：Mexican Hat和Morlet生态用小波识别的主周期与沙丘的延伸距离接近，即梭梭分布格局的波动周期与沙丘长度基本一致；同时Morl生态用小波能在较小尺度辨别局部聚集特征；通过特征尺度下突变点的检验，发现只有突变点显著尺度，才能对未来格局有较好的预测；影响梭梭空间分布格局的因素有沙丘形态、坡位和土壤因素。
关键词： 生态用小波    周期    多尺度突变与预测    梭梭    
Periodic Characteristics of Distribution Pattern of Haloxylon ammodendron in Gurbantunggut Desert Based on Eco-Used Wavelet
Song Yuyang1, 2, Li Yuanyuan1, Li Mingyan1     
1. Department of Forestry, Agricultural College, Shihezi University Shihezi 832003;
2. Key Laboratory of Environment and Ecology in Western China, Ministry of Education Northwest A & F University Yangling 712100
Abstract: In this paper, the eco-used wavelet with Mexican Hat and Morlet was used to research the wave characteristic of Haloxylon ammodendron distribution pattern in three sites and three dune types. The results showed that: the eco-used wavelet with Mexican Hat and Morlet educed the primary cycle which was closed to the extension distance of sand dunes, suggesting that the length of sand dunes was consistent with the wave cycle of H. ammodendron distribution pattern. The application of Morlet wavelet in smaller scales was able to identify the characteristic of portion accumulation. By the examination of mutation point for characteristic scale, the result showed that It is only at the significant mutation points in which the method can well predict the future distribution pattern of H. ammodendron. This study indicated some factors, such as the sand dunes shape, slope position and soil factors, affected the Haloxylon ammodendron distribution pattern.
Key words: eco-used wavelet    cycle    multi-scale abrupt change and prediction    Haloxylon ammodendron    

小波在分析格局和周期的过程中具有明显的优越性。小波函数可以利用伸缩和平移等运算功能对空间序列进行多尺度局部化分析，能够准确地找到空间序列的大小尺度，以研究不同尺度(周期)随空间的演变情况(Cui，1995)。生态学中常用的研究格局变化的小波函数为Mexican Hat和Morlet，一些学者应用小波分析了生物多样性、冠层的特征尺度、林窗分布规律等(祖元刚等，1999; Brosofske et al.，1999; 张瑾等，2007)。

但是小波分析的前提是构造合适的基本函数，只有满足非常严格的限制才能成为一个可用的小波函数。生态学上常用的这2个小波，由于周期相差较大，无法同时使用。为此，Torrence等(1998)调整了Mexican Hat和Morlet原始小波的周期，使得2个小波的周期更接近。对生态学家来说在研究同一现象时，由于各自采用的时间和空间尺度大小不一，这种差异会导致小波分析在生态格局中产生错误的周期辨别和定位，结论往往差别很大(Mi et al.，2005)。

古尔班通古特沙漠是中国最大的固定、半固定沙漠。在一定降水条件下，多种植物生长在沙漠表面(穆元伟等，2005)。其中梭梭(Haloxylon ammodendron)是古尔班通古特沙漠的建群树种，该树种对风蚀沙埋适应性较强。一些学者分析了梭梭种群格局(常静等，2006)，探讨了古尔班通古特沙漠植被格局与环境间的关系，认为在大尺度上影响植被分布格局的环境因子主要为土壤理化性质，在小尺度上主要为地貌形态、土壤水分和盐碱含量等因素(钱亦兵等，2007)。然而上述学者并没有从不同尺度对梭梭的周期性波动特征进行研究。本研究用2个生态用小波Mexican Hat和Morlet，在周期一致的前提下研究梭梭分布格局的周期性特征、多尺度突变分析和趋势预测，以期获得在一定区域内梭梭分布格局的周期性变化规律。

1 研究区概况

古尔班通古特沙漠南缘(85°59'14″—86°18'04″E，45°01'68″—45°06'19″N)为研究区。全年降雨量小于120 mm，而春夏降水量约占全年降水总量的2/3，全年日照2 600~3 100 h，≥ 10 ℃年积温3 267~3 661 ℃。沙漠内部植被覆盖率20%~30%，植被以梭梭为主，还有心叶驼绒藜(Ceratoides ewersmanniana)和琵琶柴(Reaumuria soongorica)等物种。

2 研究方法 2.1 样地设置与土壤化学性质测定

研究地点设在奎屯130团、石河子148团和精河82团。在每一研究地点选择3种沙丘类型，分别是平行状沙丘、梁窝状沙丘和树杈状沙丘，共设9块样地。每块样地包含沙垄背风坡、沙垄顶部、沙垄迎风坡和丘间平地，长度为140~340 m不等(视沙丘的延伸情况而定)，宽度为40 m。将每块样地划分为5 m×5 m的相邻网格，记录每一网格内梭梭的数量。

在每一样地的沙垄顶部、丘间平地、沙垄背风坡和沙垄迎风坡分别选取1 m2样方，在样方的0~10和10~30 cm土层各取1个土样，每一样地共取8个土样，将同一地点相同坡面的土样混合测定土壤的理化指标。用重铬酸钾容量法测定土壤有机质含量;烘干称质量法测定土壤含水量;用残渣烘干法和电导法测定土壤含盐量(含Ca2+，Mg2+，Na+，Cl-，SO42-，HCO3-和CO32-)，用酸度计测定土壤pH值。不同地点的土壤化学性质见表 1。

表 1 不同地点的土壤化学性质 Tab.1 Chemical property of soil in different sites
2.2 分析方法

小波分析采用Mexican Hat和Morlet生态用函数(Torrence et al.，1998)，函数表达式和相关参数见表 2。利用公式(1)进行小波变换，再将扩展的小波系数去掉，得到所需小波系数，并依公式(2)计算小波方差。

表 2 Mexican Hat和Morlet生态用小波的周期T与尺度a的关系① Tab.2 Relationship between cycle T and scale a of eco-used wavelet with Mexican Hat and Morlet

若f(t)是一个可测的、平方可积的函数，即具有有限的能量f(t)∈L2(R)，L2(R)为f(t)的矢量空间，R为实数集。则连续小波变换定义为信号f(t)的小波基函数内积:

$ \begin{array}{l} {W_f}(a,b) = < f(t),{\varphi _{a,b}}(t) > = \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \int_{ - \infty }^\infty {f(t){\varphi _{a,b}}(t)} dt = \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \frac{1}{{\sqrt a }}\int_{ - \infty }^\infty {f(t)\varphi \left( {\frac{{t - b}}{a}} \right)} dt; \end{array} $ (1)
$ Var(a) = \int_{ - \infty }^\infty {|{W_f}(a,b){|^2}db} 。 $ (2)
式中: t为时间; a为尺度因子，反映小波的周期长度; b为平移因子，反映时间上的平移; φa，b(t)，f(t)，Wf(a，b)和Var(a) 分别代表小波函数、信号(待分析变量)函数、小波系数和小波方差，其中小波系数的实部定义为WCR，小波系数的实部和虚部的模平方的和定义为WPS。

经过小波变换后，f(t)展开为小波级数，即:

$ f(t) = \sum\limits_{j,k \in z} {{d_{i,j}}{\varphi _{i,j}}} 。 $ (3)
式中: Wf(a，b)为方便用di，j来表示，这样f(t)就被表示成了各种分辨率小波的线性组合，其中di，j就是对应于小波函数φi，j的小波系数。

数据分析采用MATLAB7.1(Math Works Inc，USA)软件进行，小波分析时在每一组数据两端进行数据加垫，以消除边缘效应。本研究采用SPSS11.5(SPSS Inc，USA)的Independent-samples T Test 模块进行突变点检测(谢江波等，2008)，one-way ANOVA模块进行显著性检验; 用DPS中的逐步回归进行多元线性回归分析。

3 结果与分析 3.1 梭梭分布格局的波动特征

小波分解层次决定时频窗的大小，当分解层次为a时，实际能够分辨的频率可变为原信号频率的1/a，对应横轴方向的分析距离为原信号的a倍(胡昌华等，2008)。经过小波变换后，从小波方差(图 1)和WCR图(图 2)上可以清楚地看到多个特征尺度的周期性规律。对于平行状沙丘: 当a为17或18时，小波方差存在一个明显的波峰。Morlet生态用小波显示出一些大小不同的波峰，如图 1中，130团在尺度a为38，18和9处都有波峰，在它的WCR图上也能看到同样的波动特征(图 2)，只是a为9和38时图像不具有明显的周期性波动特征。当a为18时Mexican Hat和Morl的周期性波动最明显，同时在WPS图上显示贯穿整个样带(图 3)。由此可知，平行状沙丘中的主要波动周期为165~180 m。

图 1 3个地点3种沙丘类型梭梭分布格局的Mexican Hat和Morlet小波方差 Fig. 1 Variances of Mexican Hat and Morlet wavelets of H. ammodendron distribution pattern in three dune types of three sites
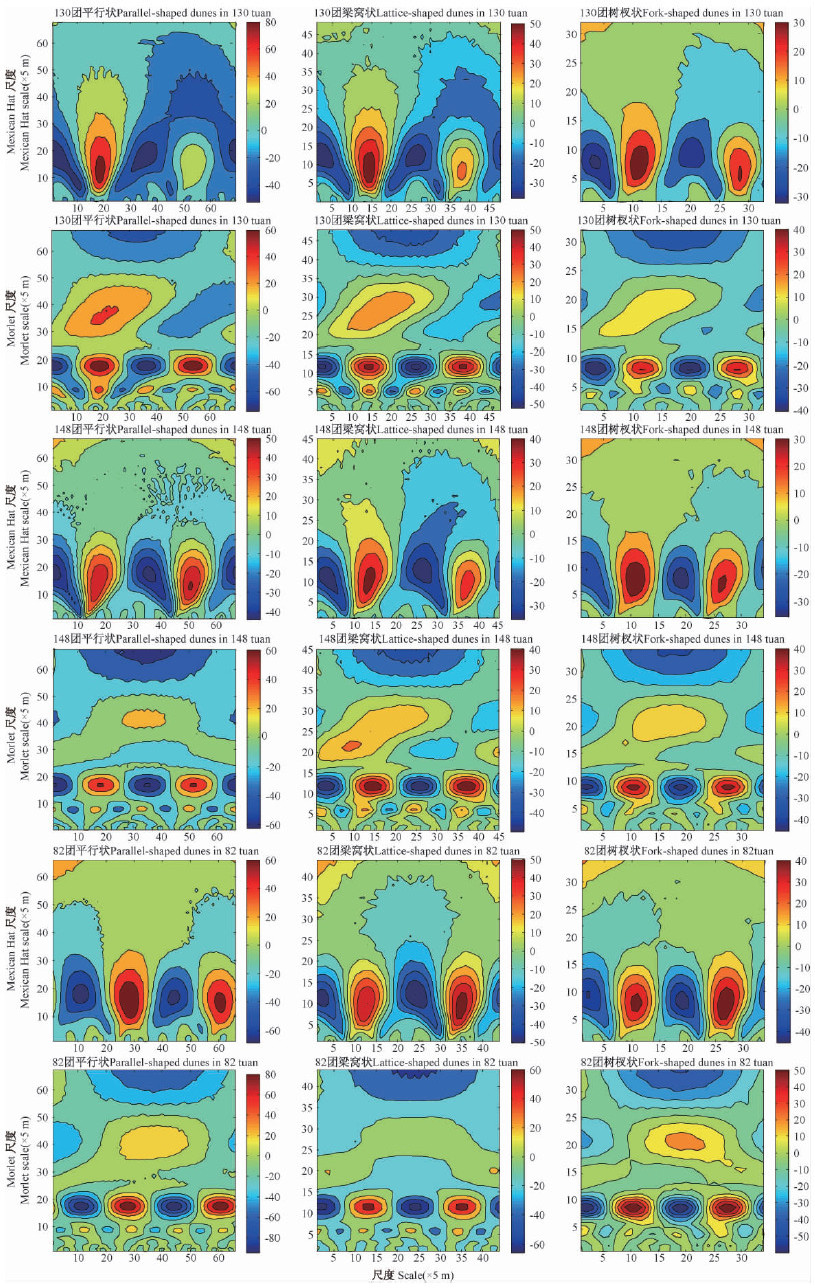图 2 3个地点3种沙丘类型梭梭分布格局的Mexican Hat和Morlet WCR图 Fig. 2 WCR of Mexican Hat and Morlet wavelets of H. ammodendron distribution pattern in three dune types of three sites
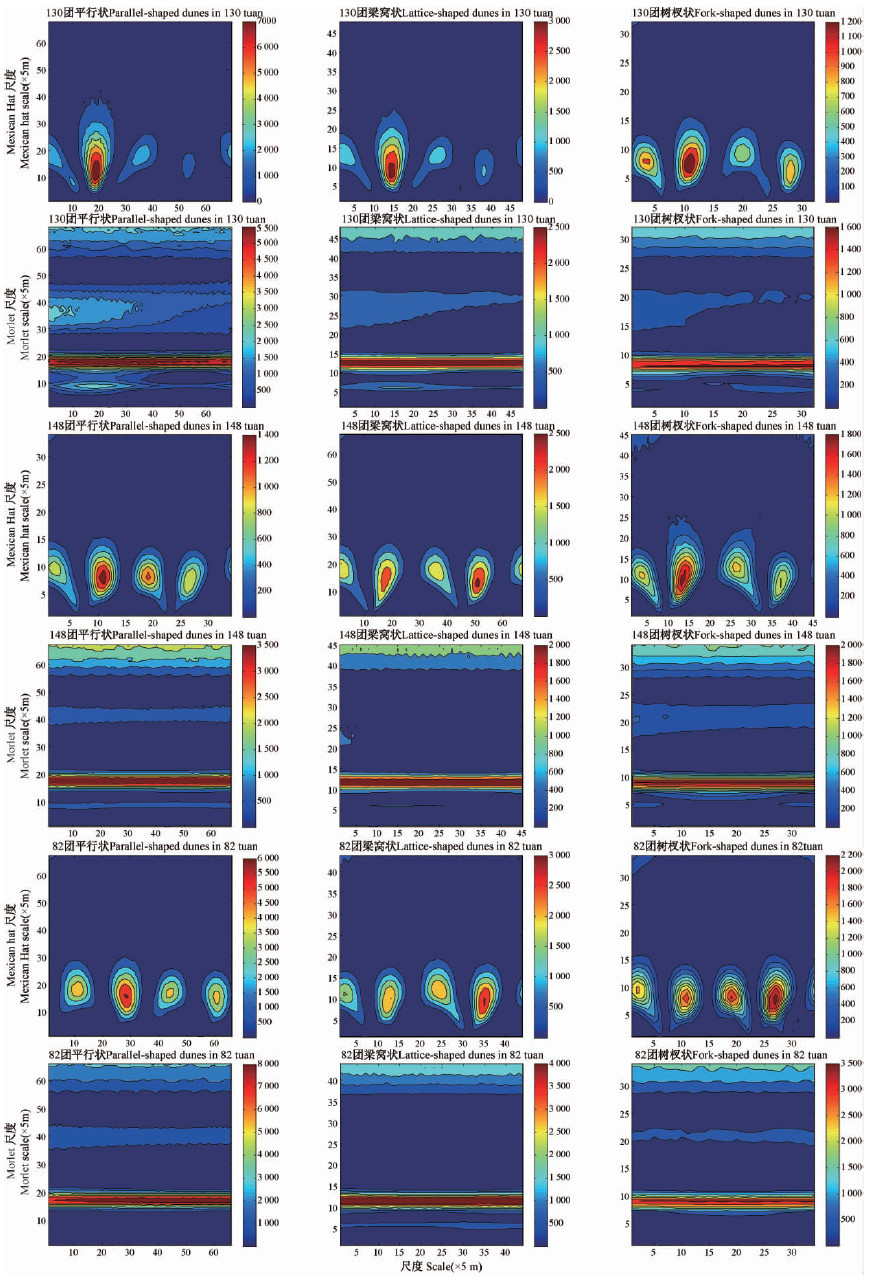图 3 3个地点3种沙丘类型梭梭分布格局的Mexican Hat和Morlet的WPS图 Fig. 3 WPS of Mexican Hat and Morlet wavelets of H. ammodendron distribution pattern in three dune types of three sites

对于梁窝状和树杈状的沙丘，梭梭的分布存在类似的规律。虽然沙垄背风坡、沙垄顶部、沙垄迎风坡和丘间延伸距离有差异，但并不影响它们空间分布格局的周期性特征。同样这2类沙丘表面梭梭的分布周期也是与沙丘的延伸距离密切相关。梁窝状沙丘在a为11或12时，Mexican Hat的小波方差出现了明显的波峰。Morlet小波发现了一些大小不同的波峰，如图 1中，148团梁窝状沙丘在a为28，21，12和6时都存在波峰，但是以a为12时的波峰为主波峰，周期性波动最明显，梁窝状沙丘梭梭空间格局的主要波动周期为100~120 m。树杈状沙丘在a为8时，Mexican Hat小波出现明显的波峰。同时Morlet小波也可以显示出一些波峰(图 1)，其中a为8时为主波峰，具有明显的周期性波动特征，因此，树杈状沙丘梭梭空间格局分布的主要波动周期为70~80 m。

3.2 特征尺度下的突变分析及趋势预测

从3个地点特征尺度下的主周期小波系数图可以看出(图 4)，Mexican Hat小波只有1个特征尺度，Morlet小波可能有多个特征尺度。而特征尺度对应的小波系数图像不一定具有稳定性，因此要对突变点进行检测，检测后突变不显著的点删去(表 3中130团Morlet分析中，a为9时，0.237＜ t0.05)。由表 3可知，Morlet生态用小波有多个显著突变点，而Mexican Hat只有1个。从小波的奇异特性可知，小波系数通过零点的地方，说明梭梭数量的分布在此样方发生了突变，有可能逐渐增多，也有可能逐渐减少。对于不同的沙丘，梭梭数量从沙垄背风坡、坡顶、迎风坡开始明显增多，到了丘间，梭梭数量又开始减少。经过如此往复，就形成了一个周期性变化的格局。由此可知，利用下一个波动周期就可以预测不同坡面梭梭数量的变化。例如130团经过Mexican Hat和Moretl生态小波分解梭梭空间分布格局的主要波动周期为165 m，以此主周期可以预测梭梭格局发展的未来趋势(图 4)，这与一些学者观测到的结果一致(钱亦兵等，2006)。

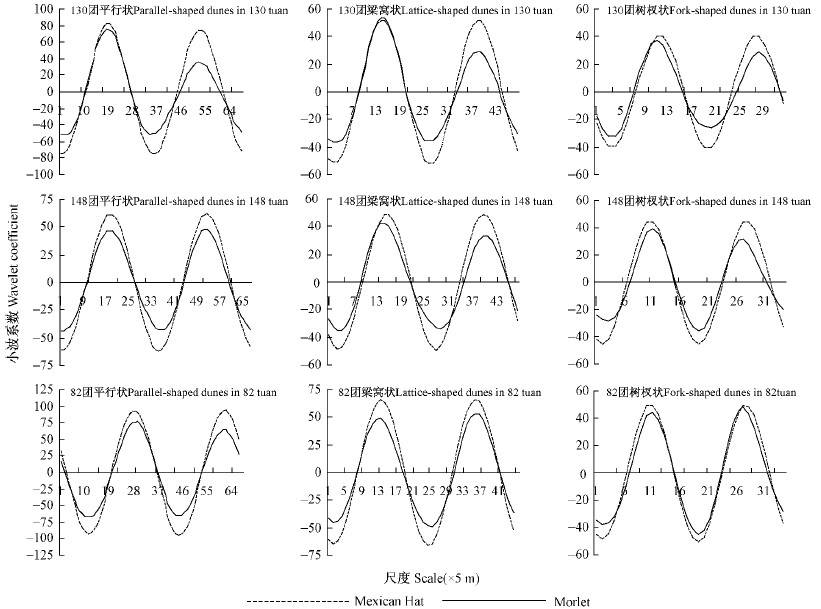图 4 3个地点3种沙丘类型梭梭分布格局的Mexican Hat和Morlet的主周期小波系数 Fig. 4 Wavelet coefficient of primary cycle using Mexican Hat and Morlet wavelets of H. ammodendron distribution pattern in three dune types of three sites
表 3 特征尺度下突变点的检验① Tab.3 Examination of mutation point for characteristic scale
3.3 影响梭梭空间格局的因素

梭梭的数量分布随不同沙丘类型的变化而变化。从散点图(图 5)可知，梭梭空间分布格局的周期性特征与沙丘的延伸距离具有高度一致性。并且不同生境内不同坡位沙垄背风坡、沙垄顶部、沙垄迎风面和丘间的梭梭分布数量差异显著(表 4)。

图 5 3个地点3种沙丘类型梭梭分布散点图 Fig. 5 Scatter diagram of H. ammodendron distribution in three dune types of three sites
表 4 3个地点不同坡位梭梭数量的差异显著性分析① Tab.4 Difference significance analysis of H. ammodendron amount in different slope positions of three sites

从逐步回归分析可知，影响梭梭空间分布格局的土壤化学因子有土壤有机质含量、土壤pH值、土壤含盐量和土壤含水量，其他因子影响较小不参与回归分析。回归方程为: y=-26.60x1+3.99x2+4.31x3+0.40x4，R=0.503 00，F=1.27。x1为土壤含水量，x2 为土壤含盐量，x3 为土壤pH值，x4为土壤有机质含量。分析结果表明，影响梭梭空间分布格局的土壤因子排序为土壤含盐量＞土壤含水量＞土壤pH值＞土壤有机质含量。

4 结论与讨论

古尔班通古特沙漠地处半封闭的准噶尔盆地中，沙漠南缘发育大量新月型沙丘、平行状沙丘、蜂窝状沙丘。多数沙垄呈现南北方向，地貌形态变化不大，植被在空间上的分布格局受沙垄形态的影响(钱亦兵等，2007)。谢江波等(2008)利用原始Mexican Hat小波发现地形基频为110 m左右，认为波峰所在位置为垄顶，是梭梭集中分布带; 波谷所在位置为丘间，没有梭梭分布，并且认为在一定程度上植被的数量分布受地形变化的影响(谢江波等，2007)。本研究发现，在一定区域内梭梭分布格局的主周期不仅受地形影响，还和土壤成分有关。局部土壤条件较好时，梭梭表现出聚集生长，反之表现出非聚集生长。点格局在分析梭梭的分布格局时，发现梭梭种群格局倾向于聚集分布，且集中分布在0~50 m尺度范围内(常静等，2006;宋于洋等，2010)。利用Morlet生态小波分析也发现，许多样地在0~50 m的范围内也存在聚集现象(图 2)，这种小尺度的格局特征是土壤成分作用的结果。通过对相邻坡面单位面积内梭梭数量的显著性分析，发现相邻地形之间梭梭数量分布存在显著差异，说明梭梭数量波动是随地形变化而变化的。其数量随背风坡-坡顶-迎风坡-丘间的变化表现出较少-极少-多-较多的特点，这种尺度(中尺度)与各沙丘坡面的长度一致。

梭梭分布格局的周期性特征除了与地形、土壤成分有关外，还与立地条件的稳定与否有关系，由于立地条件是否稳定决定着物种的更新策略(Masatoshi et al.，1996; Tang et al.，2002)，进而影响梭梭的分布格局。古尔班通古特沙漠沙丘的不同位置表现出不同的稳定性，沙丘背风坡由于坡度大、沙埋和沙鼠的啃啮，梭梭的数量较少; 顶部受到严重风蚀，土壤条件不利于梭梭的萌发和定居，梭梭的数量最少; 迎风坡坡度小、土壤水分居中，梭梭分布较多; 丘间地水分条件最好，但是由于盐碱较重，导致其梭梭数量比迎风坡少。此外，由于梭梭种子的散布属风媒传播，因此在不同地形的分布概率表现出很大差异。同时不同母树的分布及其密度也能影响梭梭的空间分布格局。

参考文献(References)
[1] 常 静,潘存德,师瑞锋. 2006. 梭梭-白梭梭群落优势种种群分布格局及其种间关系分析.新疆农业大学学报, 29(2): 26-29.(2)
[2] 胡昌华,李国华,周 涛. 2008.基于MATLAB7.X的系统分析与设计——小波分析.西安: 西安电子科技大学出版社.(1)
[3] 穆元伟,雷加强, 石泽云. 2005.古尔班通古特沙漠工程沙害形成的环境分析.干旱区研究, 22(3): 350-353.(1)
[4] 钱亦兵,吴兆宁,张立运,等. 2007.古尔班通古特沙漠植被与环境的关系.生态学报, 27(7):2802-2811.(2)
[5] 钱亦兵,张立运,唐自华,等. 2006.古尔班通古特沙漠88°E沿线风沙土理化性状的纵向分异.干旱区地理, 29(6): 784-789.(1)
[6] 宋于洋,李园园,张文辉.2010.基于Ripley的K(r)函数和分形维数的梭梭种群空间格局.应用生态学报, 21(4):827-835.(1)
[7] 谢江波,刘 彤,崔运河,等. 2008.多尺度上的多物种格局——以莫索湾四种灌木及其生境为例.生态学报,28(5):2176-2191.(2)
[8] 谢江波,刘 彤,魏 鹏,等. 2007.小波分析方法在心叶驼绒藜(Ceratoides ewersmanniana)空间格局尺度推绎研究中的应用.生态学报,27(7):2704-2714.(1)
[9] 张 瑾,贾宏涛,盛建东.2007.北疆荒漠植被梭梭林立地土壤特征及其空间变异性研究.新疆农业大学学报,30(2):33-37.(1)
[10] 祖元刚,赵则海,丛沛桐,等.1999.兴安落叶松林(Larix gmelinii)林窗分布规律的小波分析研究.生态学报,19(6):927-931.(1)
[11] Brosofske K D, Chen J, Crow T R, et al. 1999.Vegetation responses to landscape structure at multiple scales across a Northern Wisconsin, USA, pine barrens landscape. Plant Ecology, 143(2): 203-218.(1)
[12] Cui J T. 1995.An Introduction to Wavelets. Xi'an:Xi'an Jiaotong University Press.(1)
[13] Masatoshi H, Kazuhiro H, Michior F, et al. 1996. Vegetation structure in relation to micro-landform in an evergreen broad-leaved forest on Amami Ohshima Island, south-west Japan. Ecological Research, 11(3): 325-337.(1)
[14] Mi X C, Ren H B, Ouyang Z S, et al. 2005.The use of the Mexican Hat and the Morlet wavelets for detection of ecological patterns. Plant Ecology, 179(1): 1-19.(1)
[15] Tang C Q, Ohsawa M. 2002.Coexistence mechanisms of evergreen, deciduous and coniferous trees in a mid-montane mixed forest on Mt. Emei, Sichuan, China. Plant Ecology, 161(2):215-230.(1)
[16] Torrence, Compo G P. 1998. A practical guide to wavelet analysis-with significance and confidence testing// Frequency Asked Questions. [EB/OL].[2012-01-08]. http://paos.colorado.Edu/reaserch/wavelets/.(2)