游憩林是以满足人们休闲、娱乐、健身和疗养等各种游憩需求为目标，具有适合开展游憩活动的自然条件和人工设施的林分(陈鑫峰等，2000)，具有一定的美学价值，同时具有涵养水源、净化空气、保护生物多样性等多种功能。福建将乐国有林场在游憩林抚育管理方面滞后，森林游憩及其他多功能未得到充分发挥，因此，对游憩林合理的经营管理，提高其林分质量和充分发挥其多功能成为当地游憩林经营的关键问题。结构化森林经理对此研究具有重要的理论和实际意义，其实质即调整合理的林分空间结构。

林分空间结构能够反映树木的空间分布、竞争优势及其空间生态位，很大程度上影响着林分的生长、发育和稳定性，进而决定林分的功能(惠刚盈等，2001； 郑丽凤等，2006； 赵春燕等，2010)。按照结构化森林经理的观点，林分空间结构可从以下方面加以描述： 树种空间隔离程度(汤孟平等，2004)、林木个体大小(惠刚盈等，1999)、林木个体在水平地面上分布格局(Aguirre et al.， 2003)等(惠刚盈等，2003)。相应描述游憩林林分空间结构的定量指标有混交度、大小比数、聚集指数、竞争指数和开敞度等。在林分空间结构指数的研究中，其最重要的参数就是空间结构单元的确定，即对象木周围相邻木 n的选取，但n的取值大小一直存在争议。n取值过大可能把非最近邻木纳入计算范围； n取值过小时则不能兼顾对象木周围所有最近邻木的可能情形，这2种状况会导致林分空间结构指数估计存在偏差(汤孟平等，2009)。在过去的研究中，惠刚盈等(2001)指出的n为4被广泛应用； 近年来，一些学者对n的取值进行改进，提出采用Voronoi图确定空间结构单元。已有学者对Voronoi图方法和传统方法进行比较分析，两者在计算一些空间结构指数时具有较高的一致性，对混交度、大小比数和竞争指数的计算没有差异(汤孟平等，2007； 赵春燕等，2010； 郝月兰，2012)。

目前，已有学者用Voronoi图对原始林、天然次生林、紫楠(Phoebe sheareri)风景林和马尾松(Pinus massoniana)阔叶混交林等不同类型林分空间结构进行了初步探讨(刘奉强等，2010； 邓送求等，2010； 邵芳丽等，2011； 俞晓凌等，2011)。近年来Voronoi图在树木竞争分析(汤孟平等，2007)、界定最近邻木(郝月兰，2012)的应用日渐增多，但杉木(Cunninghamia lanceolata)游憩林林分空间结构的研究还未有相关文献报道。

本研究以福建将乐国有林场的杉木游憩林为对象，对典型林分样地内单株树木进行定位调查，借助Voronoi 图和Delaunay三角网确定最佳空间结构单元，采用聚集指数、混交度、大小比数、竞争指数和开敞度5 个指数分析其空间结构特征，以期为该区游憩林的林分结构调控及质量提升提供参考。

研究区位于福建省三明市将乐国有林场 (117°05′—117°40′ E，26°26′—27°04′ N)。平均海拔400～800 m，最高海拔1 203 m，最低海拔140 m； 年均气温18.7 ℃，年均降水量1 669 mm，年均蒸发量1 204 mm，全年无霜期287天，土层深厚，土壤肥沃，以红壤为主，并分布有黄红壤。试验区内植物种类丰富，除优势树种杉木外，还有马尾松 、木荷(Schima superba)、毛竹(Phyllostachys edulis)、火力楠(Michelia macclurei)、木油桐(Vernicia montana)、南酸枣(Choerospondias axillaris)、泡桐(Paulownia fortunei)、楝叶吴萸(Evodia glabrifolia)、木芙蓉(Hibiscus mutabilis)、苦槠栲(Castanopsis sclerophylla)和盐肤木(Rhus chinensis)等树种。

在对试验区杉木游憩林进行详细踏查的基础上，选取典型林分设置样地。由于试验区地形破碎，为确保样地立地条件一致，根据林分实际情况设置20 m×30 m、20 m×20 m、30 m×15 m和20 m× 15 m 这4种类型样地共13块。样地具有代表性，主要树种为杉木、毛竹和马尾松，且距离游憩道至少5 m。样地概况见表 1。对每块样地内胸径大于3 cm 的林木进行每木检尺并采用相邻格子法 (5 m×5 m)进行坐标定位调查，测量其胸径、树高、枝下高以及东西南北4个方向冠幅等。

表 1 样地概况 Tab.1 Survey of sample plots

表 1 样地概况 Tab.1 Survey of sample plots 编号No. 起源Origin 龄组Age stage 面积Area/m2 树种组成Composition 株数密度Density/(individual·hm-2) 1 人工林Artificial forest 中龄林Middle-aged forest 600 6杉木4火力楠+楝叶吴萸 6 Cunninghamia lanceolata 4 Michelia macclurei+ Evodia glabrifolia 1 783 2 人工林Artificial forest 中龄林Middle-aged forest 450 9杉木1木油桐9 Cunninghamia lanceolata 1 Vernicia Montana 1 844 3 人工林Artificial forest 中龄林Middle-aged forest 400 6杉木4马尾松 6 Cunninghamia lanceolata 4 Pinus massoniana 2 650 4 人工林Artificial forest 中龄林Middle-aged forest 400 6杉木4马尾松 6 Cunninghamia lanceolata 4 Pinus massoniana 3 900 5 人工林Artificial forest 中龄林Middle-aged forest 600 6杉木4马尾松 6 Cunninghamia lanceolata 4 Pinus massoniana 3 883 6 人工林Artificial forest 中龄林Middle-aged forest 300 6杉木4毛竹 6 Cunninghamia lanceolata 4 Phyllostachys edulis 2 400 7 人工林Artificial forest 中龄林Middle-aged forest 400 5杉木5毛竹 5 Cunninghamia lanceolata 5 Phyllostachys edulis 3 275 8 人工林Artificial forest 中龄林Middle-aged forest 600 4杉木4木荷2马尾松 4 Cunninghamia lanceolata 4 Schima superba 2 Pinus massoniana 1 650 9 人工林Artificial forest 中龄林Middle-aged forest 400 6毛竹4杉木-马尾松-木油桐 6 Phyllostachys edulis 4 Cunninghamia lanceolata-Pinus massoniana-Vernicia montana 3 925 10 人工林Artificial forest 中龄林Middle-aged forest 400 7毛竹3杉木-苦槠栲 7 Phyllostachys edulis 3 Cunninghamia lanceolata-Castanopsis sclerophylla 3 400 11 人工林Artificial forest 中龄林Middle-aged forest 300 7毛竹3杉木 7 Phyllostachys edulis 3 Cunninghamia lanceolata 4 200 12 人工林Artificial forest 中龄林Middle-aged forest 400 6马尾松3杉木1火力楠 6 Pinus massoniana 3 Cunninghamia lanceolata 1 Michelia macclurei 1 625 13 人工林Artificial forest 中龄林Middle-aged forest 600 5马尾松4杉木1南酸枣 5 Pinus massoniana 4 Cunninghamia lanceolata 1 Choerospondias axillaris 2 500

聚集指数是 Clark和Evans 于 1954 年提出的简单最近邻体分析方法，是最早采用的与距离有关的空间格局指数，它是指相邻最近单株距离的平均值与随机分布下期望的平均距离之比，以此作为空间分布格局的检验指标(Clark et al.， 1954)，其计算公式如下：

式中： R为聚集指数； r_i为第 i 单株树木到其最近邻木的距离； N为样地株数； F为样地面积。R<1，表明林木有聚集分布的趋势； R=1，表明林木有随机分布的趋势； R>1，表明林木有均匀分布的趋势； 如果R趋向于0，则表明树木之间的距离越来越密集。

混交度被定义为对象木与其n 株最近邻木为非同种的概率(惠刚盈等，2001)，其计算公式为：

式中： $ \bar M$ 为林分平均混交度； M_i为对象木i 的混交度； n为对象木i的最近邻木株数； 当对象木i 与最近邻木j 非同种时，v_ij =1，否则v_ij=0。混交度的取值范围为0～1，混交度越大说明对象木周围非同种的树木越多，即树种空间隔离程度越大。

大小比数是指大于对象木的最近邻木数占n 株最近邻木的比例(惠刚盈等，1999)，其计算公式为：

式中： $ \bar U$ 为林分平均大小比数； U_i为对象木i 的大小比数； 相邻木j 比参照树i 小，k_ij=0，否则k_ij=1。大小比数量化了对象木与其相邻木的关系，大小比数越大说明比对象木大的相邻木越多，林木分化程度越高。大小比数可以用胸径、树高或冠幅等因子表达，本研究选择胸径和树高作为指标测定林木分化程度。

竞争指数是表示林木竞争强烈程度的数量指标，常用的竞争指数可分为与距离有关的和与距离无关的两大类。在与距离有关的单木竞争指标中，国内外应用最多的是Hegyi(1974)提出的简单竞争指标。计算公式为：

式中： CI_i为对象木i的竞争指数； $ \overline {CI} $ 为样地内所有对象木竞争指数； d_j为竞争木j的胸径； d_i为对象木的胸径； L_ij为对象木i与竞争木j之间的距离。竞争指数越小，表明对象木具有较大的生长活力，在竞争中处于较有利的地位。

开敞度是指林分内任意一株对象木到n株最近邻木的水平距离与该最近邻木高度比值的均值(邓送求等，2010)。计算公式为：

式中： K_i为对象木i的开敞度； $ \bar K$ 为林分平均开敞度； D_ij为对象木i与最近邻木j的水平距离； H_ij为最近邻木j的树高。开敞度可以反映林内光照条件和林木营养空间的大小，开敞度越大表明林内光照条件越强，林木生长空间越充足。

借助ArcGIS 10.0，由树木点位置生成Delaunay三角网和Voronoi 图。设P为林分树木点的集合，p_i(i=1，2，…，n)为样地内不同的树木点，每个点的Voronoi区域表示为V(p_i)对平面的分割，Vp_i={p|d(p，p_i)≤d(p，p_j)}i=1，2，…，n，所有点的Voronoi区域的集合V(P)为： V(P)={V(P₁)，V(P₂)，…，V(P_n)}。V(P)把平面划分为n个多边形区域，每个多边形包含且只包含1个p_i点。Delaunay三角网是连接所有具有公共边的Voronoi多边形中心点所形成的三角网。Delaunay三角网与Voronoi图互为对偶图形，以此建立的Delaunay三角网和Voronoi图具有以下特点： 每个Voronoi多边形内仅包含1株林木，因此对象木的最近邻木数与其相邻多边形的个数相等； 对象木的最近邻木个数和以对象木为顶点的Delaunay三角形个数相等； 且对象木与最近邻木的距离即为构建Delaunay三角网相对应的三角形的边长(图 1)。林分内任意单株木和离它最近的n株相邻木就构成林分空间结构的基本单位，即林分空间结构单元。采用Voronoi图和Delaunay三角网确定的林分空间结构单元较传统最近邻木为4的方法更加灵活可靠。

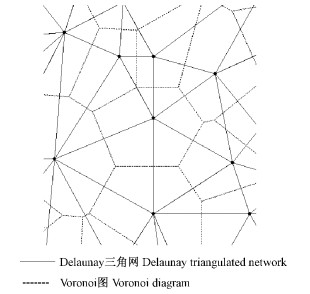	图 1 Voronoi图和Delaunay三角网 Fig. 1 Voronoi diagram and Delaunay triangulated network

由于样地边缘对象木的竞争木可能位于样地之外，必须进行边缘校正。边缘校正采用平移法，即在样地的上、下、左、右、左上、左下、右上和右下8个邻域复制原样地，形成9个样地组成的大样地(邵国凡等，1995； 周红敏等，2009)。

图 2表明，由Voronoi图和Delaunay三角网得到单株树木的最近邻木株数范围为3～11，频率分布类似左偏正态分布曲线，其中对象木的平均邻木为5.99株，以6株最近邻木所占比例最大，为30.83%。5～7株最近邻木所占比例达到77.35%，由此可见，将乐地区杉木游憩林以1株对象木和5～7株最近邻木构成的空间结构单元最为常见。本研究选取空间结构单元分布图的峰值即最近邻木 n=6分析杉木游憩林空间结构特征。

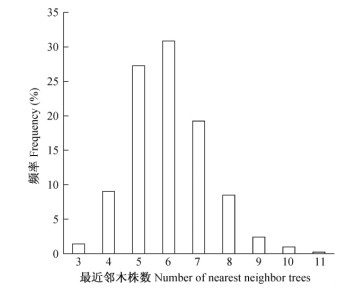	图 2 最近邻木株数分布 Fig. 2 Distribution of nearest neighbor trees number

1)聚集指数： 平均林分聚集指数R=1.05，林木个体基本上呈均匀分布。由表 2可得，有7个样地林分聚集指数大于1，呈均匀分布，5个样地林木有聚集分布的趋势，仅有1个样地为随机分布。将乐地区游憩林的这种分布状态很大程度上与人工林的起源有关。相关研究表明(陈鑫峰等，2000)，游客更为偏爱林木呈随机或均匀分布的林分，由此认为，杉木游憩林的这种分布状态较为游人喜爱，应维持这种分布状况。

表 2 各样地林木空间分布格局 Tab.2 Spatial distribution pattern of trees in each plots

表 2 各样地林木空间分布格局 Tab.2 Spatial distribution pattern of trees in each plots 样地号No. 聚集指数Aggregation index 分布类型Distribution pattern 1 1.16 均匀分布Uniform distribution 2 1.24 均匀分布Uniform distribution 3 0.84 聚集分布Aggregate distribution 4 1.00 随机分布Random distribution 5 0.97 聚集分布Aggregate distribution 6 1.13 均匀分布Uniform distribution 7 0.67 聚集分布Aggregate distribution 8 0.97 聚集分布Aggregate distribution 9 1.07 均匀分布Uniform distribution 10 0.94 聚集分布Aggregate distribution 11 1.41 均匀分布Uniform distribution 12 1.06 均匀分布Uniform distribution 13 1.20 均匀分布Uniform distribution

2)混交度： 林分平均混交度 $ \bar M$ =0.48，林分处于中等混交状态，种间相互隔离程度不高。林分中苦槠栲、楝叶吴萸和盐肤木等因个体数目较少，处于完全混交状态，通常与杉木等优势树种相伴而生。火力楠、南酸枣、木油桐和木芙蓉树种混交高于0.6，处于强度混交或极强度混交状态。毛竹、杉木和马尾松混交度为0.4～0.6，为中度混交，生长在其周围的树种有部分为同种树木。木荷混交度较小，仅为0.23，为弱度混交，表明木荷周围大部分树种为同种个体(图 3)。

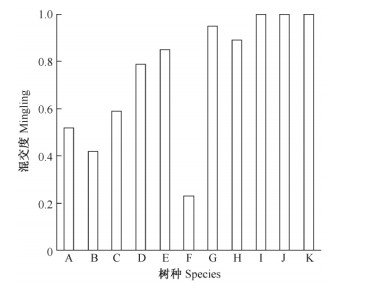	图 3 各树种混交度 Fig. 3 Mingling of each tree species A:杉木 Cunninghamia lanceolata ； B:毛竹 Phyllostachys edulis； C:马尾松 Pinus massoniana； D:火力楠 Michelia macclurei； E:南酸枣 Choerospondias axillaris； F:木荷 Schima superb； G:木油桐 Vernicia montana； H:木芙蓉 Hibiscus mutabilis； I:苦槠栲 Castanopsis sclerophylla； J:楝叶吴萸Evodia glabrifolia； K:盐肤木 Rhus chinensis. 下同。The same below.

3)大小比数： 林分平均胸径大小比数 $ \bar U$ _d=0.49，平均树高大小比数 $ \bar U$ _h=0.51，

表明林木在树高和胸径方面的分化程度都不太明显，林分处于中等竞争状态。杉木的胸径大小比数和树高大小比数分别为0.45和0.48，马尾松的胸径大小比数和树高大小比数分别为0.46和0.42，表明在杉木和马尾松的周围，较对象木大的树木不多，竞争占有一定优势，其他树种则受到不同程度的竞争压制。

4)竞争指数： 由图 4可得，杉木游憩林中主要树种竞争指数表现为毛竹>杉木>马尾松。竞争指数越大，其竞争越激烈，优势树种杉木的竞争指数 $ \overline {CI} $ =346.27，竞争较为激烈，生长活力一般，这与林内株数密度和混交度有关，可以适当调整林分结构，减小杉木的竞争，提高生长活力，进而提高杉木游憩林质量。

	图 4 各组成树种的竞争指数 Fig. 4 Competition index of each tree species

5)开敞度： 林分平均开敞度 $ \bar K$ =0.21，林木生长空间不足，林分内不够开阔。各树种开敞度为0.15～0.24(图 5)，营养空间处于严重不足和不足2种状态。林分内多数树种开敞度较小，生长空间不充足。相关研究表明，游客更偏爱多种树木混交、林内空间开阔、通透度大的林分(Ruddell et al.， 1989； 王雁等，1999； Jensen et al.， 2009)，可以适当调整林内通透程度，增大林分开阔程度，以便提高游憩林的质量。

	图 5 各组成树种开敞度 Fig. 5 Open degree of each tree species

杉木游憩林存在9种不同大小的空间结构单元，对象木的最近邻木株数有3～11株，以5～7株最为常见。基于Voronoi图和Delaunay三角网的方法能够灵活且准确地反映对象木周围最近邻木的实际情况，能够更好地描述林木之间的空间关系，杉木游憩林空间结构单元的分布呈左偏的正态分布，其均值与其峰值几乎相等，可认为杉木游憩林中每株对象木周围最近邻木为6最符合林分实际情况，这与浙江天目山常绿阔叶林(汤孟平等，2009)、金沟岭落叶松(Larix gmelinii)针阔混交林(郝月兰等，2011)、北京西山侧柏(Platycladus orientalis)游憩林(汪平等，2013)的研究结果一致，表明不同类型和功能的森林存在相似的空间结构单元。

本研究表明： 将乐地区游憩林林木空间分布格局整体处于均匀分布状态； 树种空间相互隔离程度不高，林分处于中等混交状态，个体数目较少的树种常与优势树种相伴而生，处于完全混交或强度混交状态，而杉木、毛竹和马尾松等主要树种则处于中等混交水平，林分结构稳定程度一般； 林分内林木胸径和树高的异质性均不高，林木大小处于中等分化水平； 林分内杉木的竞争能力较强，处于竞争有利位置，对阳光、水分、空气、养分等生长环境的竞争结果较为良好； 林分内的开阔程度较小，林木生长空间不足，林分游憩质量有待提高。由此认为，杉木游憩林应在维持现阶段林分状况的基础上，适当增加林内开敞度，调整林分上层林木和灌草高密程度，提高该地区的游憩价值，以便同时满足林木对生长空间和资源的需求和游客对游憩空间的需求。但由于没有充足的数据对比不同龄组游憩林的结构特征，在这一方面还有待深入研究。