林业科学  2014, Vol. 50 Issue (1): 55-62   PDF    
DOI: 10.11707/j.1001-7488.20140109
0

文章信息

童春发, 蒋安纳, 杨立委, 施季森
Tong Chunfa, Jiang Anna, Yang Liwei, Shi Jisen
WinNC2：因子交配设计遗传分析软件
WinNC2：A New Software for Genetic Analysis of Factorial Mating Design
林业科学, 2014, 50(1): 55-62
Scientia Silvae Sinicae, 2014, 50(1): 55-62.
DOI: 10.11707/j.1001-7488.20140109

文章历史

收稿日期：2013-06-06
修回日期：2013-07-20

作者相关文章

童春发
蒋安纳
杨立委
施季森

引用本文
童春发, 蒋安纳, 杨立委, 施季森. 2014. WinNC2：因子交配设计遗传分析软件[J]. 林业科学, 50(1): 55-62.
Tong Chunfa, Jiang Anna, Yang Liwei, Shi Jisen. 2014. WinNC2：A New Software for Genetic Analysis of Factorial Mating Design. Scientia Silvae Sinicae, 50(1): 55-62.  DOI: 10.11707/j.1001-7488.20140109
WinNC2：因子交配设计遗传分析软件
童春发1, 蒋安纳2, 杨立委1, 施季森1    
1. 南京林业大学林木遗传与生物技术省部共建教育部重点实验室 南京 210037;
2. 南京林业大学信息科学技术学院 南京 210037
收稿日期：2013-06-06；修回日期：2013-07-20
基金项目：国家自然科学基金面上项目（31070601）；江苏省高校优势学科建设工程资助项目（PAPD）。
通讯作者：施季森
摘要：因子交配设计在林木遗传育种研究中已经得到广泛应用，然而有关该设计的遗传参数和统计量计算还存在不少问题，这在数据不平衡情况下尤为突出。WinNC2是一个新开发的用于计算因子交配设计遗传模型参数的Windows软件，不但可以处理平衡数据，而且还可以处理不平衡数据。针对3种不同的因子交配设计遗传统计模型，该软件使用线性约束模型理论计算一般配合力和特殊配合力以及其他固定效应，使用方差分量模型计算遗传方差和协方差进而估算遗传力。对于每一个参数估计，WinNC2还给出其标准误和显著性检验统计量；对于多性状数据，WinNC2可以计算父本、母本以及父母本交互水平上2个性状的遗传相关系数及其标准误。WinNC2为林木遗传育种工作者分析因子交配设计试验数据提供了一个界面友好、易于使用的计算工具。
关键词： 因子交配设计    配合力    方差分量    遗传力    
WinNC2：A New Software for Genetic Analysis of Factorial Mating Design
Tong Chunfa1, Jiang Anna2, Yang Liwei1, Shi Jisen1     
1. Key Laboratory of Forest Genetics & Biotechnology of Ministry of Education Nanjing Forestry University Nanjing 210037;
2. College of Information Science & Technology, Nanjing Forestry University Nanjing 210037
Abstract: Although a factorial mating design has been extensively applied in forest breeding programs, there exist some problems with the design in calculating the estimates of genetic parameters and some statistics, especially when the experimental data are unbalanced. A newly developed Windows-based software (WinNC2), for calculating model parameters of the genetic factorial mating design, can not only deal with balanced data but also with unbalanced data. For three different factorial mating designs, the software estimates the general and special combining abilities of parents and other fixed effects with the restricted linear model, and calculates the genetic variance components and further the heritabilities with the random effect model. In the mean time, WinNC2 can provide standard errors and statistic tests for each parameter estimate. Furthermore, WinNC2 can also present the genetic correlation coefficient between any two traits at each level of paternal, maternal, and their interaction effects. In summary, WinNC2 is a user-friendly computing tool for forest breeders to analyze genetic models of factorial mating designs.
Key words: factorial mating design    combining ability    variance components    heritability    

因子交配设计(factorial mating design)是Comstock和Robinson(1948;1952)提出的3种北卡罗林纳(North Carolina)遗传交配设计之一，又称为NCⅡ交配设计、AB设计、析因设计或测交设计(沈熙环，1990)。这种交配设计的特点是选择1组父本和1组母本，每个父本与每个母本交配，可产生数量众多的杂交组合群体。由于该试验设计不但能提供亲本一般配合力的估计，而且还能给出特殊配合力的估计，同时也能给出有关遗传方差分量以及遗传力的估计，因此它在动植物遗传育种研究中有着极其广泛的应用。林木上，国内外先后在杉木(Cunninghamia lanceolata)、松树(Pinus)、桉树(Eucalyptus)等树种的遗传变异研究中应用了因子交配试验设计(Barnes et al.，1978;Blada，1992;郑仁华，2003;Volker et al.，2008;蒋焱等，2008;金国庆等，2008;陆钊华，2009;杨萍等，2011)。

应用因子交配设计估算遗传参数需要使用统计模型和相应的计算软件。统计模型主要是线性模型，分为固定效应模型和随机效应模型。利用线性固定效应模型可以估计出一般配合力和特殊配合力并进行相关因素的显著性检验(Wu et al.，2000;Tong et al.，2012;童春发等，2013)，而估计遗传方差分量进而估算遗传力等重要遗传参数则要使用随机效应模型(童春发等，2010;2013)。也就是说，对于每一个遗传交配设计，在分析遗传参数时需要用到2种有着本质区别的线性统计分析模型。然而，经典的林木数量遗传学著作(Wright，1976;Namkoong，1979;Williams et al.，2002;续九如，2006)在这方面没有很好的论述，使得林木育种工作者在分析林木遗传设计数据时感到诸多不便和困惑，这在不平衡数据条件下或模型含有较多因素情况下尤其突出。在软件应用方面，大多数研究者使用著名的SAS分析系统来分析林木遗传交配设计模型;但是SAS是通用的统计分析软件，不是针对特定的遗传分析模型，因此在计算林木遗传参数中存在一些不便和不足之处(童春发等，2013)。为了方便分析林木遗传参数并提供更多的统计量，近年来编写了一些Windows软件用于林木半同胞子代、巢式设计和双列杂交设计遗传模型分析(童春发等，2010;2013;Tong et al.，2012)，这些软件的主要特点在于易于使用、能处理不平衡数据以及能计算出比较全面的遗传参数。此外，国内开发的ForState(唐守正等，2009)和DPS(唐启义，2010)比较大型的数据分析系统虽然涉及到遗传交配设计模型分析，但是由于其理论方法来源于经典的数量遗传学文献资料，因此它们分析遗传模型的功能存在一定的局限性，如不能提供方差分量估计的标准误和假设检验统计量以及不平衡数据条件下遗传力估计及其标准误等。尽管在某些遗传模型计算软件开发方面已经取得一定的进展，但是对于因子交配设计统计分析目前还没有易于使用并能给出比较全面的遗传参数的计算软件。

本文根据现代线性模型理论，针对3种因子交配设计遗传模型开发了用于计算多种遗传参数和统计量的Windows应用软件WinNC2。3种因子交配设计分别为多地点多区组设计、单地点多区组设计和单地点不含区组设计。对于每一种因子交配设计，该软件使用约束线性模型理论计算一般配合力和特殊配合力以及其他固定效应，使用随机效应模型计算遗传方差分量进而计算遗传力，无论对平衡数据还是不平衡数据均可以进行计算分析。对于每一个参数估计，WinNC2还可以给出它们的标准误和显著性检验统计量。另外，WinNC2还可以计算父本、母本以及父母本交互水平上2个性状的遗传相关系数及其标准误。

1 统计模型

由于试验目的和条件的不同，因子交配设计统计分析模型也有多种形式。WinNC2主要关注3种因子交配设计统计分析模型，即多地点多区组设计、单地点多区组设计和单地点不含区组设计统计分析模型。其他因子交配设计可用同样的线性统计模型理论方法来对遗传参数进行估计和计算。

1.1 多地点多区组设计统计模型

设有m个父本、f个母本两两交配产生mf个全同胞家系，然后布置在s个地点进行子代试验，每个地点设置b个区组，每一区组若干个单株，每一个单株的数量性状值可用线性模型表示为:

$ \begin{gathered} {y_{ijklt}} = \mu + {S_i} + {B_{ij}} + {M_k} + {F_l} + {\text{M}}{{\text{F}}_{kl}} + {\text{M}}{{\text{S}}_{ik}} + \hfill \ {\text{F}}{{\text{S}}_{il}} + {\text{MF}}{{\text{S}}_{ikl}} + {e_{ijklt}} \hfill \ \end{gathered} $ (1)

式中: yijklt为第i个地点第j个区组中第k个父本与第l个母本交配子代的第t个个体数量性状值;μ为总平均值;Si为第i个地点的效应(i=1，…，s);Bij为第i个地点内第j个区组的效应(j=1，…，b);Mk为第k个父本的效应(k=1，…，m);Fl为第l个母本的效应(l=1，…，f);MFkl为第k个父本与第l个母本的交互效应;MSik为第i个地点与第k个父本的交互效应;FSil为第i个地点与第l个母本的交互效应;MFSikl为第i个地点、第k个父本和第l个母本的交互效应;MFBSijkl为第i个地点内第j个区组与第k个父本和第l母本组合的交互效应;eijklt为随机误差效应(t=1，…，nijkl)，一般假定它服从均值为0、方差为σe2的正态分布。该模型在Wright(1976)和续九如(1989;2006)中均有描述。

对于模型(1)，为了计算亲本的一般配合力和特殊配合力，将除随机效应eijklt外所有的效应都看作是固定效应，此时模型(1)被称为固定效应模型。根据约束线性模型理论可以估计配合力Mk，Fl，MFkl和其他固定效应，还可以对这些效应进行统计检验(Tong et al.，2012;童春发等，2013)。这里固定效应应满足如下约束条件:

$\left\{ \begin{gathered} \sum\limits_i {{S_i}} = 0; \hfill \\ \sum\limits_j {{B_{ij}}} = 0\left( {i = 1, \cdots s} \right); \hfill \\ \sum\limits_k {{M_k}} = 0; \hfill \\ \sum\limits_l {{F_l}} = 0; \hfill \\ \sum\limits_k {{\text{M}}{{\text{F}}_{kl}}} = 0\left( {l = 1, \cdots ,f} \right); \hfill \\ \sum\limits_l {{\text{M}}{{\text{F}}_{kl}}} = 0\left( {k = 1, \cdots ,m} \right); \hfill \\ \sum\limits_k {{\text{M}}{{\text{S}}_{ik}}} = 0\left( {i = 1, \cdots ,s} \right); \hfill \\ \sum\limits_i {{\text{M}}{{\text{S}}_{ik}}} = 0\left( {k = 1, \cdots ,m} \right); \hfill \\ \sum\limits_l {{\text{F}}{{\text{S}}_{il}}} = 0\left( {i = 1, \cdots ,s} \right); \hfill \\ \sum\limits_i {{\text{F}}{{\text{S}}_{il}}} = 0\left( {l = 1, \cdots ,f} \right); \hfill \\ \sum\limits_i {{\text{MF}}{{\text{S}}_{ikl}}} = 0\left( {k = 1, \cdots ,m;l = 1, \cdots ,f} \right); \hfill \\ \sum\limits_k {{\text{MF}}{{\text{S}}_{ikl}}} = 0\left( {i = 1, \cdots ,s;l = 1, \cdots ,f} \right); \hfill \\ \sum\limits_l {{\text{MF}}{{\text{S}}_{ikl}}} = 0\left( {i = 1, \cdots ,s;k = 1, \cdots ,m} \right); \hfill \\ \sum\limits_{k,l} {{\text{MFB}}{{\text{S}}_{ijkl}}} = 0\left( {i = 1, \cdots ,s;j = 1, \cdots ,b} \right); \hfill \\ \sum\limits_l {{\text{MFB}}{{\text{S}}_{ijkl}}} = 0\left( {i = 1, \cdots ,s;k = 1, \cdots ,m;l = 1, \cdots ,f} \right); \hfill \\ \end{gathered} \right. $ (2)

如果要计算遗传力等遗传参数，那么首先要计算遗传方差分量，此时要将模型(1)中的效应Mk，Fl，MFkl，MSik，FSil，MFSikl和MFBSijkl都看作是随机效应，并假定这些随机效应的均值为0，方差分别为σM2，σF2，σMF2，σMS2，σFS2，σMFS2和σMFBS2。根据方差分析法(Henderson，1953)可以估计这些方差分量，进一步还可以计算出其标准误以及显著性检验统计量，具体方法步骤可参考童春发等(2010;2013)。

遗传力是林木遗传分析中的一个重要指标，根据因子交配设计可以计算单株遗传力和家系遗传力。对于单株遗传力，无论数据是平衡还是不平衡，其计算表达式都是一样的。然而，对于家系遗传力，文献中只给出了平衡数据条件下的结果(Wright，1976;续九如，2006)。这里给出不平衡设计条件下家系遗传力的计算表达式。

记nijkl为第i个地点第j个区组中第k个父本与第l母本交配子代的个数，那么家系(k，l)性状的均值为:

$ \begin{gathered} {{\bar y}_{..kl.}} = C + {M_k} + {F_l} + {\text{M}}{{\text{F}}_{kl}} + \hfill \\ \frac{1}{{{n_{..kl}}}}\sum\limits_{i = 1}^s {{n_{i.kl}}} {\text{MF}}{{\text{S}}_{ikl}} + \hfill \\ \frac{1}{{{n_{..kl}}}}\sum\limits_{i = 1}^s {\sum\limits_{j = 1}^{{b_i}} {{n_{ijkl}}} } {\text{MFB}}{{\text{S}}_{ijkl}} + \frac{1}{{{n_{..kl}}}}\sum\limits_{i = 1}^s {\sum\limits_{j = 1}^b {\sum\limits_{m = 1}^{{n_{ijkl}}} {{e_{ijkl}}} } } \hfill \\ \end{gathered} $

式中: C为固定效应代数和。因此家系均值的方差为:

$ \begin{gathered} \operatorname{var} \left( {{{\bar y}_{ \cdot \cdot kl \cdot }}} \right) = \sigma _{\text{M}}^2 + \sigma _{\text{F}}^2 + \sigma _{{\text{MF}}}^2 + \hfill \\ \frac{1}{{n_{ \cdot \cdot kl}^2}}\sum\limits_{i = 1}^s {n_{i \cdot kl}^2\sigma _{{\text{MFS}}}^2} + \hfill \\ \frac{1}{{n_{ \cdot \cdot kl}^2}}\sum\limits_{i = 1}^s {\sum\limits_{j = 1}^{{b_i}} {n_{ijkl}^2} \sigma _{{\text{MFBS}}}^2} + \frac{1}{{{n_{ \cdot \cdot kl}}}}\sigma _e^2 \hfill \\ \end{gathered} $

由于数据不平衡性会导致各家系均值的方差不一致，因此取家系均值方差的平均值作为计算家系遗传力的背景，于是不平衡数据条件下家系遗传力可表示为:

$ \begin{gathered} h_{\text{f}}^2 = \frac{{\sigma _{\text{M}}^2 + \sigma _{\text{F}}^2 + \sigma _{{\text{MF}}}^2}}{{\frac{1}{{{n_{M \times F}}}}\sum\limits_{k,l} {\operatorname{var} \left( {{{\bar y}_{ \cdot \cdot kl \cdot }}} \right)} }} = \hfill \\ \frac{{\sigma _{\text{M}}^2 + \sigma _{\text{F}}^2 + \sigma _{{\text{MF}}}^2}}{{\sigma _{\text{M}}^2 + \sigma _{\text{F}}^2 + \sigma _{{\text{MF}}}^2 + {k_1}\sigma _{{\text{MS}}}^2 + {k_1}\sigma _{{\text{FS}}}^2 + {k_1}\sigma _{{\text{MFS}}}^2 + {k_2}\sigma _{{\text{MFBS}}}^2 + {k_3}\sigma _{\text{e}}^2}} \hfill \\ \end{gathered} $ (3)

式中:nM×F表示家系的个数;${k_1} = \frac{1}{{{n_{M \times F}}}}\sum\limits_{k，l} {\frac{1}{{n_{..kl}^2}}} \sum\limits_{i = 1}^s {n_{i.kl}^2} ;{k_2} = \frac{1}{{{n_{M \times F}}}}\sum\limits_{k，l} {\frac{1}{{n_{..kl}^2}}} \sum\limits_{i = 1}^s {\sum\limits_{j = 1}^{{b_i}} {n_{ijkl}^2} } ;{k_3} = \frac{1}{{{n_{M \times F}}}}\sum\limits_{k，l} {\frac{1}{{{n_{..kl}}}}} $。

1.2 单地点多区组设计统计模型

设有m个父本、f个母本两两交配产生mf个全同胞家系，然后在某个地点设置b个区组进行子代试验，每一区组若干个单株，则单株的数量性状值可用线性模型表示为:

$ {y_{ijkl}} = \mu + {B_i} + {M_j} + {F_k} + {\text{M}}{{\text{F}}_{jk}} + {e_{ijkl}} $ (4)

式中: yijkl为第i个区组中第j个父本与第k个母本交配子代的第l个个体数量性状值;μ为总平均值;Bi为第i个区组的效应(i=1，…，b);Mj为第j个父本的效应(j=1，…，m);Fk为第k个母本的效应(k=1，…，f);MFjk为第j个父本与第k个母本的交互效应;eijkl为随机误差效应(l=1，…，nijk)，并假定它服从均值为0、方差为σe2的正态分布。该模型可见于贝克尔(1987)。

同样地，根据模型(4)来估计亲本的一般配合力和特殊配合力，首先需要将效应Bi，Mj，Fk和MFjk看作固定效应，并施加如下的约束条件:

$ \left\{ \begin{gathered} \sum\limits_i {{B_i} = 0;} \hfill \\ \sum\limits_j {{M_j} = 0;} \hfill \\ \sum\limits_k {{F_k} = 0;} \hfill \\ \sum\limits_j {{\text{M}}{{\text{F}}_{jk}} = 0\left( {k = 1, \cdots ,f} \right);} \hfill \\ \sum\limits_k {{\text{M}}{{\text{F}}_{jk}} = 0\left( {j = 1, \cdots ,m} \right);} \hfill \\ \end{gathered} \right. $ (5)

然后根据线性约束模型理论来估计这些固定效应。

若要估计方差分量，则在模型(4)中将Mj，Fk和MFjk看作随机效应，并假定它们的均值为0，方差分别为σM2，σF2和σMF2。利用方差分析法可以对这些方差分量进行估计，并可以计算出估计的标准误以及检验这些参数显著性的统计量，进一步还可以计算出遗传力。

记nijk为第i个区组中第j个父本与第k个母本交配子代的个数，那么家系(j，k)性状的均值为:

$ {{\bar y}_{ \cdot jk \cdot }} = C + {M_j} + {F_k} + {\text{M}}{{\text{F}}_{jk}} + \sum\limits_{i = 1}^b {\sum\limits_{l = 1}^{{n_{ijk}}} {{e_{ijkl}}} } $

式中: C为固定效应代数和。家系均值的方差为:

$ \operatorname{var} \left({{{\bar y}_{ \cdot jk \cdot }}} \right)= \sigma _{\text{M}}^2 + \sigma _{\text{F}}^2 + \sigma _{{\text{MF}}}^2 + \frac{1}{{{n_{ \cdot jk}}}}\sigma _e^2 $

因此，根据模型(4)计算不平衡数据条件下家系遗传力的表达式为:

$ h_{f}^{2}=\frac{\sigma _{\text{M}}^{2}+\sigma _{\text{F}}^{2}+\sigma _{\text{MF}}^{2}}{\sigma _{\text{M}}^{2}+\sigma _{\text{F}}^{2}+\sigma _{\text{MF}}^{2}+{{k}_{4}}\sigma _{e}^{2}} $ (6)

式中:${{k}_{4}}=\frac{1}{{{n}_{M\times F}}}\sum\limits_{jk}{\frac{1}{n.jk}}$。

1.3 单地点不含区组设计统计模型

设有m个父本、f个母本两两交配产生mf个全同胞家系，每个家系种植若干个单株，则单株的数量性状值可用线性模型表示为:

$ {y_{ijk}} = \mu + {M_i} + {F_j} + {\text{M}}{{\text{F}}_{ij}} + {E_{ijk}} $ (7)

式中: yijk为第i个父本与第j个母本交配子代的第k个个体数量性状值;μ为总平均值;Mi为第i个父本的效应(i=1，…，m);Fj为第j个母本的效应(j=1，…，f);MFij为第i个父本与第j个母本的交互效应;eijk为随机误差效应(k=1，…，nij)，并假定它服从均值为0、方差为σe2的正态分布。该模型比较简单，在Namkoong(1979)和贝克尔(1987)中均有提到。

在模型(7)中，若将Mj，Fk和MFjk看作固定效应，并施加如下的约束条件:

$ \left\{ \begin{gathered} \sum\limits_i {{M_i} = 0;} \hfill \\ \sum\limits_j {{F_j} = 0;} \hfill \\ \sum\limits_j {{\text{M}}{{\text{F}}_{ij}} = 0\left( {j = 1, \cdots ,f} \right);} \hfill \\ \sum\limits_j {{\text{M}}{{\text{F}}_{ij}} = 0\left( {i = 1, \cdots ,m} \right);} \hfill \\ \end{gathered} \right. $ (8)

则按约束线性模型参数估计方法可以计算出一般配合力和特殊配合力。若将Mj，Fk和MFjk看作随机效应，并假定它们的均值为0，方差分别为σM2，σF2和σMF2，则使用方差分析法可对这3个方差分量进行估计。

记nij为第i个父本与第j个母本交配子代的个数，那么家系(i，j)性状的均值为:

$ {\bar y_{ \cdot jk \cdot }} = \mu + {M_i} + {F_j} + {\text{M}}{{\text{F}}_{ij}} + \frac{1}{{{n_{ij}}}}\sum\limits_{k = 1}^{{n_{ij}}} {{e_{ijk}}} $

家系均值的方差为:

$ \operatorname{var} \left({{{\bar y}_{ \cdot jk \cdot }}} \right)= \sigma _{\text{M}}^2 + \sigma _{\text{F}}^2 + \sigma _{{\text{MF}}}^2 + \frac{1}{{{n_{ij}}}}\sigma _e^2 $

因此，根据模型(7)计算不平衡数据条件下家系遗传力的表达式为:

$ h_{\text{f}}^2 = \frac{{\sigma _{\text{M}}^2 + \sigma _{\text{F}}^2 + \sigma _{{\text{MF}}}^2}}{{\sigma _{\text{M}}^2 + \sigma _{\text{F}}^2 + \sigma _{{\text{MF}}}^2 + {k_5}\sigma _e^2}} $ (9)

式中:${{k}_{5}}=\frac{1}{{{n}_{\text{M}\times \text{F}}}}\sum\limits_{jk}{\frac{1}{{{n}_{ij}}}}$。

2 结果

针对因子交配设计遗传统计分析模型(1)，(4)和(7)，用VC++2008编写了Windows计算软件WinNC2。该软件分别根据固定效应和随机效应模型理论给出亲本配合力估计和遗传方差分量估计，进一步还给出遗传力和遗传相关系数的估计，无论对平衡数据还是不平衡数据都能进行处理计算。WinNC2界面友好，使用方便，可以自由下载使用，其网址为: http://fgbio.njfu.edu.cn/tong/WinNC2/WinNC2.htm。

图 1显示了WinNC2分析3种因子交配设计的Excel输入数据格式。图 1a中第1列至第4列分别为地点、区组、父本和母本的代码，第5列起为性状1，2，3的值等，这里只列出了2个性状值。显然图 1b和图 1c是从图 1a简化而来的，其每列意义如表头所示。使用者可点击WinNC2的File菜单打开某个输入数据，然后选择合适的因子交配设计分析模型计算，计算结果会在窗口中显示，并在输入数据所在的目录里找到计算结果文件result.txt。

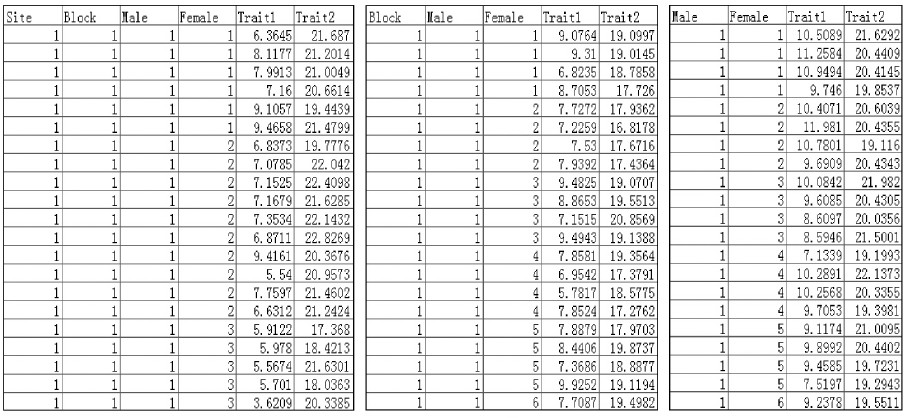图 1 WinNC2 用于分析(a) 模型(1)、(b) 模型(4) 和(c) 模型(7)的Excel 输入数据格式 Fig. 1 The Excel format of input data for (a) model (1)，(b) model (4) and (c) model (7) in WinNC2

图 2给出了WinNC2对1个性状使用固定效应模型计算模型(1)的部分结果。对于每个性状，WinNC2首先对模型本身和各个因素进行检验，然后给出亲本的一般配合力和特殊配合力以及其他固定效应的估计、标准误、显著性检验t统计量和p值，接着给出父本配合力两两之间、母本配合力两两之间和父母本特殊配合力两两之间是否有显著差异的t检验统计量。从图 2的前部分可以看出，对于性状1模型本身和各个因素经检验都是极显著的。从图 2的参数估计部分可以看出，母本3和4的一般配合力以及父本5和母本4的特殊配合力都是极显著的，而父本1和母本1的特殊配合力则不显著。

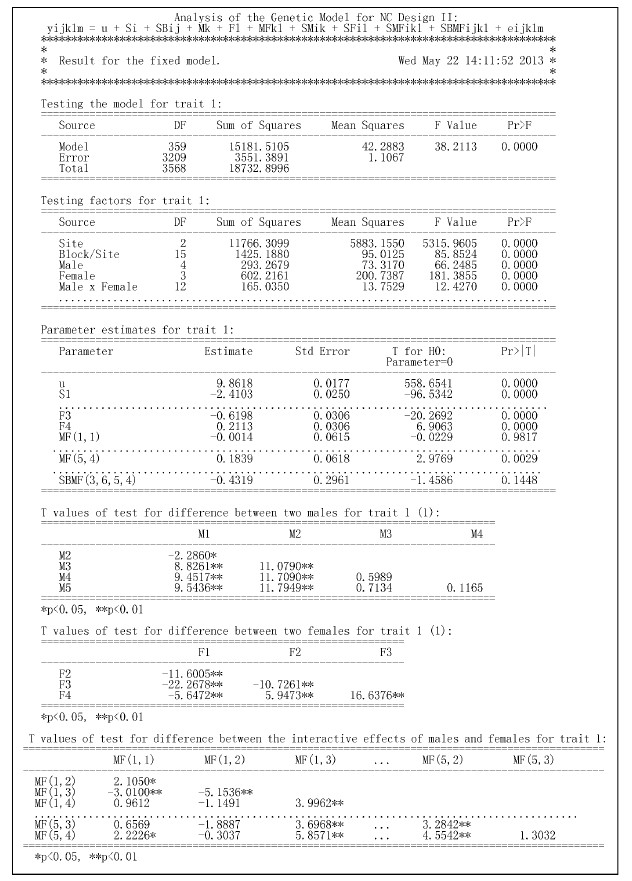图 2 WinNC2分析固定效应模型计算结果 Fig. 2 Output of analyzing fixed effects model with WinNC2

图 2的后部分表明，父本3，4和5一般配合力两两之间差异不显著，而其他情况则是显著的，母本一般配合力两两之间差异都是显著的，特殊配合力两两之间差异有些显著而其他情况则不显著。图 3是WinNC2对2个性状使用随机效应模型计算模型(1)的结果。对于每个性状，WinNC2均给出每个方差分量的估计、标准误、F检验统计量和p值，同时还计算出单株遗传力和家系遗传力以及它们的标准误。对于2个以上的性状，软件还进一步计算出两两性状间在父本效应、母本效应和父母本交互效应水平上的遗传相关系数。

图 3 WinNC2分析随机效应模型计算结果 Fig. 3 Output of analyzing random effects model with WinNC2
3 讨论

因子交配设计在林木遗传育种研究中是一个重要的交配试验设计，它能提供父母本及其大量子代的遗传信息，因此在遗传分析上能够获得比较全面的遗传参数，如双亲的一般配合力和特殊配合力、各个因子上的遗传方差分量等。然而，在实际分析因子交配设计试验数据时，不少研究者会遇到许多困难:一是没有意识到在用因子交配设计进行遗传分析时会用到2类线性模型，即固定效应模型和随机效应模型，使得即使有通用的软件(如SAS等)也不能得到很好的应用;二是实际获取的数据往往会在不同的水平上是不平衡的，使得经典的方差分析法在稍微复杂的模型上难以实现。本文开发的Windows应用软件WinNC2能让使用者很方便地分析计算3种类型的因子交配设计遗传参数，包括一般配合力和特殊配合力、遗传方差分量、单株遗传力和家系遗传力以及性状间的遗传相关系数，同时还提供遗传参数估计的标准误和假设检验的统计量以对遗传参数估计作进一步评估。

同常用的统计软件相比，WinNC2简单易用，使用者无须按照遗传模型编写代码，只要打开数据文件然后选择适当的因子交配设计模型就能计算出相应的遗传参数。SAS是著名的统计分析系统，但它不是针对特定遗传分析模型。如果用SAS分析因子交配设计模型的配合力，就需要使用者熟悉SAS编程并将固定效应模型的约束条件考虑进去(Wu et al.，2000;Tong et al.，2012;童春发等，2013)，这让很多不熟悉统计模型的研究者无所适从。SAS的VARCOMP等过程可以用于计算因子交配设计模型的方差分量，但是不能直接计算出遗传力和遗传相关系数，并且如果选择使用方差分析(ANOVA)法，那么SAS还不能给出方差分量估计的标准误。最近，ASReml软件(Gilmour et al.，2009)在育种领域里应用较多，但是此软件也是一个通用软件，需要使用者熟悉特定遗传模型并编写代码以实现相应的计算。

遗传力在林木遗传育种学中是一个重要的遗传参数，利用因子交配设计可以计算单株遗传力和家系遗传力(Wright，1976;续九如，1989;2006)，甚至还可以计算父本家系遗传力和母本家系遗传力(Holland et al.，2003;续九如，1989;2006)。文献中有关家系遗传力的计算公式一般都是针对平衡试验设计的，但是没有说明是如何推导出来的。本文针对3种因子交配设计推导出了不平衡数据条件下家系遗传力的计算公式，这些公式可以简化成平衡数据条件下遗传力的计算公式。例如，在平衡设计条件下，公式(3)可以简化成Wright(1976)和续九如(1989;2006)中全同胞家系遗传力计算公式。但是令人遗憾的是，在Wright(1976，p247)中这一公式分母中项σMF2多了因子1/FM，而在续九如(2006)公式(4-28)中分子分母项σM2和σF2的系数都存在问题。只有续九如(1989)公式(23)同本文公式(3)的简化结果一致。至于不平衡数据条件下因子交配设计的父本家系遗传力和母本家系遗传力计算似乎有点复杂，留待以后作进一步的研究。

方差分量的假设检验问题比较复杂，其统计方法仍然在不断发展研究过程中。对于平衡设计试验数据，一般用Wald法对方差分量是否为零进行显著性检验(Wald，1941;王松桂等，2007)。对于不平衡设计试验数据，本文采用Ofversten(1993)提出的重抽样法(resampling)对方差分量进行显著性检验。由于模型(1)涉及到地点等较多的因素，因此在方差分量假设检验过程中本文多次使用了Ofversten重抽样法。当然，Ofversten方差分量假设检验方法在因子交配设计模型中应用的统计性质需要作进一步评估，可以考虑将置换法(permutation)(Fitzmaurice et al.，2007)应用到方差分量假设检验中去以便同Ofversten(1993)方法作比较。

参考文献(References)
[1] 贝克尔 W A. 1987. 数量遗传学手册. 区靖祥, 译. 北京: 科学出版社.(2)
[2] 蒋焱, 龚建英, 雷布先, 等. 2008. 杉木测交系设计子代遗传分析. 江西林业科技, (6):16-18.(1)
[3] 金国庆, 秦国峰, 刘伟宏, 等. 2008. 马尾松测交系杂交子代生长性状遗传分析. 林业科学, 44(1):70-76.(1)
[4] 陆钊华. 2009. 尾叶桉种内种间交配遗传分析及F1选择研究. 北京: 中国林业科学研究院博士学位论文.(1)
[5] 沈熙环. 1990. 林木育种学. 北京: 中国林业出版社.(1)
[6] 唐启义. 2010. DPS数据处理系统. 北京: 科学出版社.(1)
[7] 唐守正, 郎奎建, 李海奎. 2009. 统计和生物数学模型计算(ForStat教程). 北京: 科学出版社.(1)
[8] 童春发, 卫巍, 尹辉, 等. 2010. 林木半同胞子代测定遗传模型分析. 林业科学, 46(1): 29-35.(3)
[9] 童春发, 杨立伟, 蒋安纳, 等. 2013. 不平衡巢式设计遗传模型分析. 林业科学, 49(1): 1-8.(6)
[10] 王松桂, 史建红, 尹素菊, 等. 2007. 线性模型引论. 北京: 科学出版社.(1)
[11] 续九如. 1989. 树木遗传力估算方法的研究. 内蒙古林学院学报, (1): 32-45.(3)
[12] 续九如. 2006. 林木数量遗传学. 北京:高等教育出版社.(6)
[13] 杨萍, 石志玲, 陈晓阳. 2011.杉木3种交配设计试验种子品质的遗传分析. 华南农业大学学报, 32(4):67-70.(1)
[14] 郑仁华. 2003. 不同年龄杉木无性系交配的研究. 林业科学, 39(Sp.1):81-86.(1)
[15] Barnes R D, Mullin L J. 1978. Three-year height performance of Pinus elliottii Engelm. var. elliottii × P. taeda L. hybrid families on three sites in Rhodesia. Silvae Genetica, 27:217-223.(1)
[16] Blada I. 1992. Analysis of genetic variation in a Pinus strobus×P. griffithⅡ F1 hybrid population. Silvae Genetica, 41(4/5):282-289.(1)
[17] Comstock R E, Robinson H F. 1948. The components of genetic variance in populations of biparental progenies and their use in estimating the average degree of dominance. Biometrics, 4(4): 254-266.(1)
[18] Comstock R E, Robinson H F. 1952. Estimation of average dominance of genes// Gowen J W. Heterosis. Ames, IA: Iowa State University Press, 494-516.(1)
[19] Fitzmaurice G M, Lipsitz S R, Ibrahim J G. 2007. A note on permutaion tests for variance components in multilevel generalized linear mixed models. Biometrics, 63(3): 942-946.(1)
[20] Gilmour A R, Gogel B J, Cullis B R, et al. 2009. ASReml User Guide Release 3.0. Hemel Hempstead, UK: VSN International Ltd.(1)
[21] Henderson C R. 1953. Estimation of variance and covariance components. Biometrics, 9(2):226-252.(1)
[22] Holland J B, Nyquist W E, Cervantes-Martinez C T. 2003. Estimating and interpreting heritability for plant breeding: An update. Plant Breeding Reviews, 22: 9-112.(1)
[23] Namkoong G. 1979. Introduction to quantitative genetics in forestry. U. S. Department of Agriculture Forest Service Technical Bulletin 1588.(2)
[24] Ofversten J. 1993. Exact tests for variance components in unbalanced mixed linear models. Biometrics, 49(1): 45-57.(2)
[25] Tong C F, Liu G X, Yang L W, et al. 2012. GSCA: new software and algorithms to analyse diallel mating designs based on restricted linear model. Silvae Genet, 61(3): 126-132.(4)
[26] Volker P W, Potts B M, Borralho N G M. 2008. Genetic parameters of intra-and inter-specific hybrids of Eucalyptus globulus and E. nitens. Tree Genetics and Genomes, 4(3): 445-460.(1)
[27] Wald A. 1941. On the analysis of variance in case of multiple classifications with unequal class frequencies. The Annals of Mathematical Statistics, 12(3): 346-350.(1)
[28] Williams E R, Matheson A C, Harwood C E. 2002. Experimental design and analysis for tree improvement. Collingwood, VIC, Australia: CSIRO Publishing.(1)
[29] Wright J W. 1976. Introduction to forest genetics. New York: Academic Press, Inc.(5)
[30] Wu H X, Matheson A C. 2000. Analysis of half-diallel mating design with missing crosses: Theory and SAS program for testing and estimating GCA and SCA fixed effects. Silvae Genet, 49(3):130-137.(2)