文章信息
- 施拥军, 刘恩斌, 周国模, 沈振明, 俞淑红
- Shi Yongjun, Liu Enbin, Zhou Guomo, Shen Zhenming, Yu Shuhong
- 基于随机过程的毛竹笋期生长模型构建及应用
- Bamboo Shoot Growth Model Based on the Stochastic Process and Its Application
- 林业科学, 2013, 49(9): 89-93
- Scientia Silvae Sinicae, 2013, 49(9): 89-93.
- DOI: 10.11707 /j.1001-7488.20130912
-
文章历史
- 收稿日期:2012-09-04
- 修回日期:2013-04-11
-
作者相关文章
2. 浙江农林大学环境与资源学院 临安 311300;
3. 临安市林业科技推广总站 临安 311300
2. School of Environmental and Resource Sciences, Zhejiang A&F University Lin'an 311300;
3. Lin'an City Forestry Science and Technology Extension Station Lin'an 311300
树木生长量反映了森林生态系统中林木与环境之间物质循环和能量流动的复杂关系,树木生长量的准确测定,无论是对林业研究,或是对政府部门制定相关林业政策都有着十分重要的意义。建立一定的生长模型来推算树木生长量是生产实践中常用的方法(邓红兵等,1999; 雷相东等,2009; 王丽梅等,2004)。林木的生长模型主要分为单木生长模型和林分模型,其中单木生长模型是研究林分的生长模型和林分结构模型基础。目前,常见的单木生长模型有: 双曲线型、伯塔兰菲(Bertalanffy)、单分子(Mitscherlich)、查曼-理查兹(Chapman-Richards)、坎派兹(Gompertz)、逻辑斯蒂(Logistic)、考尔夫(Korf)等(王丽梅等,2004; 罗辑等,2000; 邓红兵等,1999; 葛剑平等,1992; 刘平等,2008; 代全林等,2002; 韦善华等,2011),但这些方程都不满足描述树木生长曲线族的特性(惠刚盈等,1996; Sloboda,1971),也有学者用林窗模型研究树高的动态生长(Rasche et al.,2012),但也不具有生长曲线族的特性。
众所周知,林木生长不可避免地受到许多随机因素的影响,在整个生长过程中,这些因素对它的影响时大时小,有单独作用,也有综合作用,目前还不能将其全部精确地测定出来,即便能测定出来,其因素之间的关系也是随机变化的。因此在描述树木生长过程时,把林木测树因子一般看作随机变量,把林木生长过程视为一个随机过程来进行描述。
毛竹(Phyllostachys edulis)是种特殊的植物,从笋高度为30 cm 左右的出笋期开始到其枝叶完全展开终止,毛竹处于爆发式生长期,其高生长对后期的碳素积累能力产生重要影响。毛竹笋期生长规律的研究可为研究毛竹整个生长周期的固碳特征以及科学调控竹林经营提供理论依据。目前有关毛竹笋期爆发式生长规律的研究少见报道。Sloboda 生长方程能确保拐点参数的生物意义,可以拟合多形指数曲线(惠刚盈等,1996),故本文以 Sloboda 生长模型为基础,应用随机过程理论来研究毛竹笋期生长过程,其目的: 1)确定毛竹笋期生长模型,揭示毛竹高生长规律; 2)随机过程理论方法的应用,为树木生长过程的研究提供新的理论基础; 3)对解释毛竹超强固碳功能,编制毛竹生长过程表,指导毛竹生产实践及预估毛竹林的生长提供理论依据。
1 理论与方法 1.1 毛竹笋期生长随机过程的描述毛竹Ω作为一个样本空间,每株毛竹ω是一个样本,部分毛竹组成的集合是事件,以Ω某些子集组成的集合类Λ为事件域,并在Λ上定义一个集合函数P,满足: 1)P(A)≥0, A ∈Λ; 2)P(Ω)=1; 3)Ai ∈Λ,i =1,2,…,两两互不相容,且有$P\left({\sum\limits_{i = 1}^\infty {{A_i}} } \right)= \sum\limits_{i = 1}^\infty {P\left({{A_i}} \right)} $,则称 P 为Λ上的概率。由此可以定义一个有关毛竹的概率空间(Ω,Λ,P),有了这个概率空间就可以对毛竹笋期生长的随机过程作如下描述。
由于随机因素的干扰与立地条件的不同,使不同毛竹在某一特定时间t的累计生长量 X(ω,t)(ω∈Ω)是随机变化的,对于固定的时间t,(ω,t)(ω∈Ω)是一个随机变量,则{X(t,ω),t ∈ T,$T \subset R$}是一个随机变量族,当ω∈Ω固定时,则X(t,ω),t ∈ T,$T \subset R$)是某一株毛竹的生长函数,也称为样本曲线,当ω,t都固定时,X(t,ω)是一个确定的实数,其含义是某一特定时间,某一毛竹样本的累计生长,对于随机变量 X(t,ω)(t固定且t∈ T)所有可能的取值,称为毛竹生长过程的状态空间,而每一个可能取的值称为状态。由此可见毛竹生长过程是一个随机过程。
1.2 毛竹笋期高生长的随机过程模型由上可知,随机过程模型能描述毛竹样本空间Ω的笋期生长,结合毛竹生长特性,所构建的模型满足如下条件(Sloboda,1971): 1)坐标原点具有结点的特性,各样本曲线应有共同的起始点,且X轴为所有曲线的切线; 2)每条样本曲线有各自的拐点,且这些拐点可组成一条(x,y)曲线; 3)每一条样本曲线具有各自的渐近线,均与X轴平行; 4)各样本曲线之间互不相交。根据这4个条件,Sloboda(1971)利用数学分析手段,推导出如下生长微分方程:
| $ \frac{{{\rm{d}}y}}{{{\rm{d}}t}} = \frac{{by}}{{{t^a}{\rm{In}}{{\left({\frac{c}{y}} \right)}^ \circ }}} $ | (1) |
| $ y = c\exp \left({ -d} \right)\exp \left({\frac{b}{{\left({a -1} \right){t^{a -1}}}}} \right)。 $ | (2) |
再对该方程进行整理得:
| $ X\left({w,t} \right)= {\rm{SI}}\exp \left({\frac{b}{{k{t^k}}}} \right)。 $ | (3) |
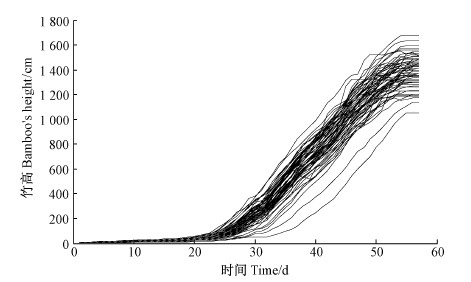 |
图 1 实测毛竹笋期生长曲线
Fig. 1 Measured bamboo shoots growth curve
|
均值函数、自相关函数与标准差函数是随机过程最基本的特征函数,假设随机变量SI的概率密度函数为f(SI),则毛竹笋期生长随机过程的均值函数为:
| $ m\left(t \right)= E\left[ {X\left({w,t} \right)} \right] = \int {{\rm{SI}}\exp \left({\frac{b}{{k{t^k}}}} \right)f\left({{\rm{SI}}} \right)d} {\rm{SI}}。 $ | (4) |
自相关函数为:
| $ \begin{array}{*{20}{c}} {R\left({{t_1},{t_2}} \right)= E\left[ {X\left({w,{t_1}} \right)X\left({w,{t_2}} \right)} \right] = }\ {\int {{\rm{SI}}\exp \left({\frac{b}{{k{t_1}^k}}} \right)\cdot SI\exp \left({\frac{b}{{k{t_2}^k}}} \right)\cdot f\left({{\rm{SI}}} \right)d} {\rm{SI}}} \end{array} $ | (5) |
标准差函数为:
| $ \sigma \left(t \right)= \sqrt {R\left({t,t} \right)-{m^2}\left(t \right)}。 $ | (6) |
研究区设在浙江省西北部的临安市青山镇,地理位置为119°47'22″ E,30°13'45″ N,海拔为50~130 m。属中亚热带季风气候。年平均气温15.9 ℃,平均气温2 ℃。年均降雨量1 613 mm,平均降雨日158天,降水明显集中在春季和初夏。平均日照时数1 920 h,年无霜期237天,土壤为黄红壤。
2.2 数据获取与处理在青山镇的人工经营毛竹林中,随机选取140株毛竹(笋)作为测量样本,在毛竹(笋)边上竖立序号标牌进行样本标记。从2009年3月18日竹笋刚刚出土开始,每日定时(13: 00—17: 00)对其进行高生长的连续跟踪测量,至2009年5月12日,毛竹开始抽枝展叶结束高生长为止,共连续测量57天。当竹笋高度小于2 m 时,采用钢卷尺测量其高度; 当竹笋高度超过2 m 时,采用徕卡 TCR 702Xrange 型精密全站仪根据“悬高测量法”精确测量其高度,测量标称精度达到毫米级。对采集到的样本数据进行质量检验,去除记录信息不全(研究过程中竹笋死亡或遭到人为损坏)和有粗差的样本,最后得到有效毛竹样本数据95株。样本数据的地径为8~17cm,生长稳定后的竹高为1 053.2~1 672.9 cm。
3 结果与分析 3.1 毛竹实测笋期生长曲线根据实测的140株毛竹高生长数据,把各个时刻具有最大生长量与最小生长量的曲线作为上包迹线与下包迹线,再在上下包迹线所形成的范围内选取90株典型毛竹样本数据,利用 matlab 软件的 plot 函数作典型毛竹生长曲线(图 1)。
从图 1可以看出,毛竹笋期高生长在55天左右完成,在第25天附近可以把笋期生长分为2个阶段,1~25天为第1阶段,毛竹生长较为平缓,25~55为第2阶段,毛竹处于爆发式生长。
3.2 毛竹样本函数族的拟合利用 SPSS 软件与每株调查毛竹笋期生长数据分别对(3)式进行拟合,得各株毛竹样本函数的参数k,b分别为2.184 1与-919 6.751 8,SI 的值分布在区间(1 886.272 3,3 592.196 4),各株毛竹拟合确定系数R2在0.923~0.999,这说明(3)式对每株调查毛竹样本的拟合精度都非常高,具体见图 6的蓝色曲线。
3.3 随机变量 SI、竹高的概率分布概率分布的研究方法有参数检验与非参数检验2种,参数检验需要事先给定某种分布函数,然后再对拟合分布进行检验,该方法的缺陷是事先给定何种分布,具有一定的主观随意性,而非参数检验对概率分布的描述,完全取决于给定的数据,不含任何人为主观因素。核密度估计是最常用的非参数检验方法,事实证明它对概率分布的描述优于 Weibull 分布(崔恒建等,1996)。因此本文用核密度估计来描述随机变量的概率分布。核密度估计描述随机变量SI的概率分布如图 2所示。
 |
图 2 随机变量SI的概率分布
Fig. 2 Probability distribution of random variableSI
|
为了得到随机过程的特征函数,必须要先知道SI的理论概率分布函数,从图 2可以看出随机变量SI的概率分布与正态分布非常接近,因此选用正态分布描述SI的概率分布,经 SPSS 非线性回归拟合得 σ = 306.436 1,u = 2 786.836 9,此时R2 =0.983,拟合精度非常高。
从图 1可以看出,对于给定的 t,毛竹的累计生长量是随机变量,用核密度估计描述第1阶段与第2阶段实测140株毛竹样本各个时间段累计生长量的典型概率分布图像(图 3,4)。
 |
图 3 1~25天毛竹累计生长量的概率分布
Fig. 3 Probability distribution of Moso bamboocumulative growth during 1-25 days
以上曲线是所有样本在各个时间累计生长量的典型概率分布。The above curve is typical probability distribution of all samples’s cumulative growth in each time.下同。The same below. |
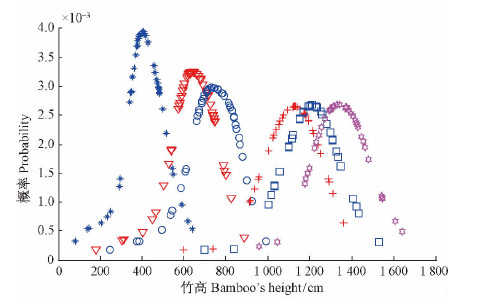 |
图 4 25~55天毛竹累计生长量的概率分布
Fig. 4 Probability distribution of Moso bamboocumulative growth during 25-55 days
|
从图 3,4可以看出: 1)随着毛竹的生长其累计生长量概率分布曲线由左偏峰逐渐转变为正态分布; 2)概率分布的峰值逐步减小,且起初减小幅度较大,后逐步变为平稳。
3.4 毛竹笋期生长随机过程的特征函数毛竹笋期生长随机过程的特征函数包括: 均值函数与方差函数(标准差函数)。但要得到标准差函数需要相关函数。由随机过程的相关理论得到毛竹笋期生长均值函数:
$ \begin{array}{*{20}{c}} {m\left(t \right)= \int {\begin{array}{*{20}{c}} {3592.1964}\ {1886.2723} \end{array}} {\rm{SI}}\exp \left({\frac{{ -9196.7518}}{{2.1841{t^{2.1841}}}}} \right)\frac{1}{{306.4361\sqrt {2\pi } }}}\ {\exp \left({ -\frac{{\left({{\rm{SI}} -2786.8369} \right)}}{{1.9319 \times {{10}^5}}}} \right)d{\rm{SI}}。} \end{array} $
用分布积分法整理得:
| $ m\left(t \right)= 2768.0452\exp \left({\frac{{ -9196.7518}}{{2.1841{t^{2.1841}}}}} \right) $ | (7) |
用 Matlab 软件的 plot 函数作90株典型毛竹笋期生长均值函数图像,见图 5,6的红色曲线,其中,图 5蓝色曲线是90株典型毛竹笋期生长的实测曲线,图 6的蓝色曲线是相应理论曲线。
 |
图 5 毛竹笋期生长实测样本曲线、均值函数曲线及标准差函数曲线
Fig. 5 Curve of practical samples,standard deviation,and mean functions of Moso bamboo shoots based on measured samples
|
 |
图 6 毛竹笋期生长理论样本曲线、均值函数曲线及标准差函数曲线
Fig. 6 Curve of exoterical samples,standard deviation,and mean
|
由于本文研究的是一个随机过程,所以相关函数 R(t1,t2)就是自相关函数。具体表达式为:
| $ \begin{array}{*{20}{c}} {R\left({{t_1},{t_2}} \right)= 7796616.5485\exp \left({\frac{{ -9196.7518}}{{2.1841{t_1}^{2.1841}}}} \right)}\ {\exp \left({\frac{{ -9196.7518}}{{2.1841{t_2}^{2.1841}}}} \right)。} \end{array} $ | (8) |
由$\sqrt {R\left({t,t} \right)-{m^2}\left(t \right)} $即可得标准差函数,用 Matlab 软件的 plot 函数作毛竹笋期生长标准差函数图像,见图 5,6的绿色曲线。
由图 5,6可得: 1)蓝色的曲线是毛竹笋期生长实测与理论样本函数,它们只是某些毛竹的样本曲线,而毛竹是一个整体性概念,任何一株毛竹都是它的一个元素,任何一些毛竹的组合都是它的一个子集,所以任何一个样本函数或任何一些样本曲线都不能表示毛竹笋期生长函数; 2)红色的曲线是其均值函数,它综合了所有样本函数的信息,理论上可以代表毛竹笋期生长曲线; 3)绿色曲线是标准差函数,表示毛竹样本曲线在各个时间t对均值函数的分散程度,所以毛竹笋期生长的第2阶段比第1阶段的分散程度要大; 4)由常用生物量模型可知,毛竹笋期生物量的累积量是地径与竹高的函数,由于毛竹笋期生长的第1阶段(1~25天),其竹高增长相对较平稳而地经不变,所以其生物量的累积量不大,但在生长的第2阶段(25~55天),因竹高处在爆发式增长阶段且地径不变,所以在该阶段其生物量的累积速度非常快,体现了毛竹超强的固碳功能; 5)生长的第1阶段,由于标准差函数较平稳,故各毛竹竹高生长量与生物量的累积量相差不大,反映了该阶段立地条件对毛竹生长量与生物量的累积量影响不大; 但在第2阶段由于立地条件的不同,使标准差函数斜率迅速变大,各毛竹竹高生长量与生物量的累积量差异较大,且生长的时间越长这种差异就越大,反映了该阶段立地条件对毛竹生长量与生物量的累积量影响非常大。
4 结论由于很多随机因素的干扰,任何树种的生长过程实质上是一个随机过程,因此必须用随机过程来描述。Sloboda 生长方程可以描述多形指数曲线,具有很多其他生长模型不具备的特点,同时能确保拐点参数的生物意义(惠刚盈等,1996),结合已有研究成果、随机过程理论及实测数据,本文得到如下结论。
1)毛竹笋期生长在大约55 天完成,其生长过程可以分为2个阶段: 1~25天为第1阶段,该阶段毛竹生长比较缓慢,25~55天为第2阶段,该阶段毛竹处于爆发式生长。
2)对于给定的生长时间,毛竹的累计生长量是随机变量,其概率分布曲线由左偏峰逐步转化为正态分布,且其分布的峰值起初显著下降,后逐步变为平稳。
3)对于不同的毛竹,(3)式所示的Sloboda生长方程参数k,b的值相同,而SI的值服从正态分布。
4)本研究给出了毛竹笋期生长随机过程模型及其特征函数(均值函数、相关函数与标准差函数),为进一步研究毛竹其他性质奠定了基础,也为研究树木生长过程提供了新的理论方法。
5)毛竹笋期生长的第1阶段,生物量的累积量不大,但在第2阶段,竹高爆发式增长,生物量的累积量非常大,体现了毛竹超强的固碳功能。
| [1] |
崔恒建,王雪峰. 1996.核密度估计及其在直径分布研究中的应用.北京林业大学学报, 18(2): 67-72. ( 1) 1)
|
| [2] |
代全林,陈存及,肖书平. 2002.茶秆竹高生长模型的比较及组合选择. 福建林学院学报, 22(2): 129-132.( 1) 1)
|
| [3] |
邓红兵,郝占庆,王庆礼. 1999.红松单木高生长模型的研究.生态学杂志, 18(3): 19-22. ( 2) 2)
|
| [4] |
葛剑平,李景文,郭海燕. 1992.天然红松树木生长特征与林分结构的研究.东北林业大学学报, 20(2): 9-16.( 1) 1)
|
| [5] |
惠刚盈,盛炜彤. 1996. Sloboda树高生长模型及其在杉木人工林中的应用.林业科学研究, 9(1): 37-40.( 3) 3)
|
| [6] |
雷相东,李永慈,向玮. 2009.基于混合模型的单木断面积生长模型.林业科学, 45(1): 74-79.( 1) 1)
|
| [7] |
刘平,马履一,贾黎明. 2008.油松人工林单木树高生长模型研究.林业资源管理, (5): 50-56.( 1) 1)
|
| [8] |
罗辑,程根伟,杨忠,等. 2000.贡嘎山暗针叶林不同林型的优势木生长动态.植物生态学报, 24(1): 22-26.( 1) 1)
|
| [9] |
王丽梅,潘辉,魏建文. 2004. Sloboda树高生长模型在火炬松人工林中的应用研究.北华大学学报:自然科学版, 5(2): 159-161.( 2) 2)
|
| [10] |
韦善华,覃静,朱贤良,等. 2011.南宁地区灰木莲人工林生长规律研究.西北林学院学报, 26(5): 174-178.( 1) 1)
|
| [11] |
Rasche L, Fahse L, Zingg A, et al. 2012. Enhancing gap model accuracy by modeling dynamic height growth and dynamic maximum tree height. Ecological Modelling, 232: 133-143.( 1) 1)
|
| [12] |
Sloboda B. 1971. Zur Darstellung von Waehstumsprozessen mit Hilfe von Differentialgleiehungen erster Ordnung. Mitteilungen der Baden-Wuerttembergisehen Forstliehen Versuehs-und Forsehungsanstalt, 32: 1-109.( 3) 3)
|
 2013, Vol. 49
2013, Vol. 49

