林业科学  2013, Vol. 49 Issue (8): 65-74   PDF    
DOI: 10.11707/j.1001-7488.20130810
0

文章信息

符利勇, 孙华
Fu Liyong, Sun Hua
基于混合效应模型的杉木单木冠幅预测模型
Individual Crown Diameter Prediction for Cunninghamia lanceolata Forests Based on Mixed Effects Models
林业科学, 2013, 49(8): 65-74
Scientia Silvae Sinicae, 2013, 49(8): 65-74.
DOI: 10.11707/j.1001-7488.20130810

文章历史

收稿日期：2012-11-08
修回日期：2013-03-23

作者相关文章

符利勇
孙华

引用本文
符利勇, 孙华. 2013. 基于混合效应模型的杉木单木冠幅预测模型[J]. 林业科学, 49(8): 65-74.
Fu Liyong, Sun Hua. 2013. Individual Crown Diameter Prediction for Cunninghamia lanceolata Forests Based on Mixed Effects Models. Scientia Silvae Sinicae, 49(8): 65-74.  DOI: 10.11707/j.1001-7488.20130810
基于混合效应模型的杉木单木冠幅预测模型
符利勇1, 孙华1,2     
1. 中国林业科学研究院资源信息研究所 北京 100091;
2. 中南林业科技大学林业遥感信息工程研究中心 长沙 410004
收稿日期：2012-11-08；修回日期：2013-03-23
基金项目：林业公益性行业重点项目"我国典型森林类型健康经营关键技术研究"(201004002); 林业公益性行业科研专项"林分结构与生长模拟技术研究"(201104028)。
通讯作者：孙华
摘要：以湖南省黄丰桥国有林场103块样地共2 461株杉木为例,建立单木冠幅模型。由于所调查数据是在不同立地条件下相同样地中重复观察得到,数据间存在明显相关性,为解决此问题,将考虑立地指数和样地对冠幅生长的随机影响,即建立嵌套2水平非线性混合冠幅模型。从12个常用林分模型中选出较好的冠幅直径模型作为构建混合模型的基础模型。除胸高直径外,还考虑其他17个林分或树木因子对冠幅的影响。通过指标AIC(akaike information criterion)和对数似然确定最佳形式参数随机效应组合类型,用指数函数、幂函数以及常数加幂函数3种形式的残差方差模型消除异方差,最后对混合模型和传统回归模型进行比较及评价。结果表明: 逻辑斯蒂形式的冠幅直径模型[模型(13)]拟合效果较好,选择为基础模型; 胸径、冠底高、树高和样地优势高是影响冠幅的主要因子; 幂函数消除异方差效果最好; 与立地指数相比,立地指数与样地的嵌套效应对冠幅影响更大; 模型(15)的嵌套2水平比总体平均水平和立地指数水平预测精度高,相比于模型(13)有明显改进。本文主要为方法研究,对于其他树种可以用相似方法构建冠幅模型。
关键词： 杉木    单木冠幅模型    嵌套2水平非线性混合模型    异方差    
Individual Crown Diameter Prediction for Cunninghamia lanceolata Forests Based on Mixed Effects Models
Fu Liyong1, Sun Hua1,2     
1. Research Institute of Forest Resources Information Techniques, CAF Beijing 100091;
2. Research Center of Forestry Remote Sensing and Information Engineering, Central South University of Forestry and Technology Changsha 410004
Abstract: An individual crown diameter model was developed based on a data set consisting of 2 461 Cunninghamia lanceolata from 103 plots located in Huangfengqiao state-owned forest farm in Hunan Province. Because of the problem of high correlation among observations taken from the same sample plot located in different levels of site index, the random effects of site index and sample plots to crown diameter were considered, namely, developing nested two levels nonlinear mixed effects canopy model. Base model that used to develop mixed model was selected from 12 commonly used models in forest. In addition to diameter at breast height, the effects of other 12 stand or trees factors to crown diameter were considered. The best random effects combination for formal parameters was determined by indexes of AIC (akaike information criterion) and logarithm likelihood. Three residual variance models of Exponential function, power function and constant plus function were used to decline the heteroskedasticity. Mixed effects model and traditional regression model were compared and evaluated finally. Results showed that crown diameter-diameter model of logistic formal had a better fit effect and was selected as base model; diameter at breast height, under branch height, height and dominant height of plot were significant factors in crown diameter model; power function had a better ability to decline the heteroskedasticity; comparing to site index, the nested effects of site index and plot played more important role in crown diameter model; the prediction efficiency of the nested two level of model (15) was higher than site index level and population average level, and obviously improved comparing with model (13). This article was mainly emphasize method research, it can be used similar method that proposed in this study to built canopy with model for other tree species.
Key words: Cunninghamia lanceolata    individual crown diameter model    nested two level nonlinear mixed effects model    heteroskedasticity    

树冠是树木进行光合作用的重要场所，它决定树木的活力和生产力，在树木生长过程中也是反映树木长期竞争水平的重要指标(Biging et al., 1992)。冠幅是树冠结构的重要特征因子之一(Spurr et al., 1980; Monserud et al., 1996; Russell et al., 2011)，在单木生长模型中常作为协变量预测树高和胸径生长量以及树木枯损等(Monserud et al., 1996; Russell et al., 2011)，同时利用冠幅计算林木的竞争指数(Wykoff，1990; Biging et al., 1995; Monleon et al., 2004; Toney et al., 2009)。此外，冠幅也是林分可视化的重要参数(雷相东等，2006)。

目前对冠幅的研究主要集中在定性和图表层面(Wykoff，1990; Monserud et al., 1996)，利用传统回归方法建立冠幅与一些林分因子，如胸高直径、树高、胸高断面积、林分密度等因子的线性关系(Gill et al., 2000; Bechtold，2004)。通常情形下，由于所分析数据来源于重复调查数据或多水平数据，如在不同立地条件下相同样地中对树木冠幅重复观察或对同一株树木不同时间段多次观察等，因此数据间可能存在明显的自相关和异相关等(Uzoh et al., 2008)。回归分析方法假定数据间相互独立且非异质性(Keselman et al., 1999; Garrett et al., 2004)，反映林分总体变化情况，无法分析不同水平或林分因子对冠幅生长的随机影响。然而，混合模型能有效地解决此类问题(Uzoh et al., 2008; 符利勇等，2012a; 2012b)。

国内外少数学者利用混合模型预测冠幅，例如，Sánchez-González 等(2008)利用单水平非线性混合效应模型构建西班牙栓皮栎(Quercus suber)冠幅模型，把样地作为随机效应因子，结果为混合模型的预测精度比普通回归模型高。但模型中只考虑对象木胸高直径和样地平均直径对冠幅的影响，对于如何利用所建模型对建模之外的样地进行预测尚未研究。对于考虑2 个及2 个以上相互嵌套的林分因子对冠幅随机影响的研究至今还未发现。基于以上问题，本研究以湖南省黄丰桥国有林场103 块样地共 2 461 株杉木(Cunninghamia lanceolata)为例，把立地指数和嵌套在立地指数中的样地作为随机效应因子，详细介绍如何利用嵌套2 水平非线性混合效应模型构建冠幅模型。文中从基础模型选型、林分变量选取、混合模型参数构造到模型预测时随机效应参数估计都始终以实用性为宗旨，保证了模型的通用性。

1 材料与方法 1.1 研究区概况

研究区位于湖南省黄丰桥国有林场，该林场呈带状横跨株洲市攸县东西部，介于113°04'—113° 43'E，27°06'—27°24'N 之间。东北部与江西的莲花、萍乡交界，东南与茶陵县接壤，西北部与株洲、醴陵毗邻。全场地貌以中低山为主，坡度介于20 ～ 35°之间。林场地处中亚热带季风湿润气候区，年均气温17. 8 ℃，年均降水量1 410. 8 mm。全场现有林地面积10 122. 6 hm2，活立木蓄积879 705 m3，森林覆盖率为86. 24%。树种主要以杉木、松类(Pinus spp.)为主，其中杉木面积3 197. 6 hm2，占用材林面积的89. 9%，蓄积593 738 m3，占96. 56%，全部为人工造林。木材资源以用材林为主，大多为中龄林、 成过熟林。

1.2 试验数据

在黄丰桥国有林场随机布置103 块样地，每块样地调查内容有胸径5 cm 以上的活立木胸径(D)、 树高(H)、冠底高(height to crown base，简称HCB)以及东南西北4 个方向的冠幅半径、样地郁闭度(canopy density，简称CD)。所调查的样地中，随机取出69 块作为建模数据，剩下34 块作为检验数据，统计信息见表 1。文中所指冠幅(crown width，简称 CW)为4 个方向的平均值。立地指数(site index，简称SI)由下式(杜纪山等，2000)计算得到:

${\text{SI = }}H{}_d\exp \left( {b/A - b/{A_0}} \right)$ (1)
式中: Hd 为优势木平均高(m); A 为林分年龄; A0 为基准年龄，b = 11. 5，A0 = 20 年。

1.3 非线性混合效应模型

嵌套多水平非线性混合效应模型，以2 水平为例，表达式为(Pinheiro et al., 2000):

$\eqalign{ & {y_{ijk}} = f\left( {{\Phi _{ijk}},vijk} \right) + {\varepsilon _{ijk}},i = 1, \cdots ,M, \cr & j = 1, \cdots ,{M_i},k = 1, \cdots ,{n_{ij}}; \cr} $ (2)
${u_i} \sim N\left( {0,{\psi _1}} \right),{u_{ij}} \sim N\left( {0,{\psi _2}} \right)$ (3)

式中: M 为第1 水平因子等级数; Mi 为第1 水平因子第i 等级对应的第2 水平因子等级数; nij 为第1 水平因子第i 等级第2 水平因子第j 等级的重复观测次数; yijk和υijk 分别为第1 水平因子第i 等级第2 水平因子第j 等级对应的第k 次重复调查时因变量和自变量的观测值; f 是关于参数向量 Φi和υi 的非线性函数; β 为p × 1 维固定效应参数; ui 为q1 × 1 维的第1 水平随机效应参数，假定服从期望为0、方差为ψ1 的正态分布; uij 为q2 × 1 维的第2 水平随机效应参数，假定服从期望为0、方差为ψ2 的正态分布; ij 为形式参数(简称形参)，它与β，ui 及uij 呈线性函数关系; Aijk，Bi，jk和Bijk 分别为β，ui和uij 的设计矩阵; εijk 为随机误差项，假定服从期望为0、方差为R 的正态分布，并假定ui，uij和误差项εijk 之间相互独立。

表1 建模数据和检验数据统计信息① Tab.1 Summary statistics for modeling and validation data sets

立地指数是影响林分生长的主要因子(Uzoh et al., 2008)。各样地间立地质量的好坏呈随机分布，因此，各样地间树木冠幅生长存在随机差异。按SI ＜ 12，12≤SI ＜13，13≤SI ＜14，14≤SI ＜ 15，15≤SI ＜ 16，16≤SI ＜17，17≤SI ＜18和SI≥18 把立地质量划分成 1 ～8 个等级。由于不同立地质量等级中嵌套着一定数量的样地，因此本研究把立地质量作为第1 水平随机效应因子，样地作为第2 水平随机效应因子，通过构建嵌套2 水平非线性混合效应模型分析立地指数、 样地以及它们之间交互作用对冠幅生长的随机影响。

1.3.1 基础模型

选用12 种冠幅－ 胸径模型作为候选基础模型，见表 2。其中，Sönmez(2009)和Sánchez-González 等(2008)利用前8 种模型对土耳其辽东云杉(Picea orientalis)和西班牙栓皮栎冠幅进行拟合，后4 种为林业上常见林分生长模型。利用平均残差(e)、残差方差(σ2)、均方误差(δ)和决定系数(R2)4 个指标选出一种拟合效果最好的模型作为构建冠幅混合模型的基础模型。平均残差(e)、残差方差(σ2)和均方误差(δ)的计算见公式(4)～(6):

$\eqalign{ \bar e = & \sum\limits_{i = 1}^M {\sum\limits_{j = 1}^{{M_i}} {\sum\limits_{k = 1}^{{n_{ij}}} {{e_{ijk}}/N} } } = \cr \sum\limits_{i = 1}^M {\sum\limits_{j = 1}^{{M_i}} {\sum\limits_{k = 1}^{{n_{ij}}} {\left( {{{\overline {{\rm{CW}}} }_{ijk}} - {\rm{\hat C}}{{\rm{W}}_{ijk}}} \right)} } } /N; \cr} $ (4)
$\xi = {\sum\limits_{i = 1}^M {\sum\limits_{j = 1}^{{M_i}} {\sum\limits_{k = 1}^{{n_{ij}}} {\left( {{e_i} - \bar e} \right)} } } ^2}/\left( {N - 1} \right);$ (5)
$\delta = \sqrt {{e^2} + \xi } $。 (6)
式中: C^Wijk 为冠幅的预测值; $\overline {{\text{CW}}} $为冠幅观测值的平均值。

表2 候选基础模型① Tab.2 Candidate base model
1.3.2 林分变量

除与胸径相关外，冠幅还受其他林分变量的影响，如树木大小和林分活力因子、立地条件因子以及林分竞争因子等(Sánchez-González et al., 2008; Sönmez，2009; 雷相东等，2006)。同时在模型中增加林分变量能降低林分或单木水平随机效应差异对冠幅的影响(Pinheiro et al., 1998)。本研究考虑的林分变量有:

树木大小和林分活力因子———林分年龄(A)、 林分密度(M)、郁闭度(CD)、树高(H)、冠底高(HCB)(Calama et al., 2004; Sánchez-González et al., 2008);

立地条件因子———立地指数(SI)(Spurr et al., 1980; Sánchez-González et al., 2008);

林分竞争因子———样地算术平均直径(MD)、 样地优势木平均高(DH)、样地优势木平均直径(DD)、样地平方平均直径(MDD)、样地中大于对象木直径树木的总株树(LDN)、样地中大于对象木直径所有树木胸高直径和(LDSD)、样地中大于对象木直径所有树木胸高直径的平均值(LDMD)、样地中大于对象木直径所有树的胸高断面积和(LDSA)、样地中大于对象木直径所有树的胸高断面积平均值、样地中大于对象木树高所有树的树高和(LHSH)、样地中大于对象木树高所有树的树高平均值(LHMH)(Uzoh et al., 2008; Sánchez- González et al., 2008)。林分变量选择标准见文献 Calama 等(2004)和Uzoh 等(2008)。

1.3.3 形式参数构造

给定基础模型后，利用评价指标AIC和对数似然Loglik 确定最优随机效应组合构造类型(Yang et al., 2011)。为避免模型参数过多，本文利用似然比检验(Fang et al., 2001):

${\text{LRT = 2}}\lg \left( {{L_1}/{L_2}} \right) = 2\left( {\lg {L_1} - \lg {L_2}} \right)$

式中: L1和L2 分别为模型1和模型2 的似然函数值，LRT 服从自由度为k1 － k2 的λ 分布。给定可靠性α = 0. 05，当LRT≥ λα(k1 － k2)拒绝原假设，说明这2 个模型差异显著; 反之，2 个模型差异不显著，故选择含随机效应参数较少的模型。

1.3.4 随机效应参数方差(ψ1和ψ2)结构

与 Calama 等(2005)的方法相似，假定ψ1和ψ2 为无结构类型，以3 × 3 维矩阵为例，ψ1 或ψ2 写为:

$\left( {\matrix{ {\sigma _1^2} & {{\rho _{12}}} & {{\rho _{13}}} \cr {{\rho _{21}}} & {\sigma _2^2} & {{\rho _{23}}} \cr {{\rho _{31}}} & {{\rho _{32}}} & {\sigma _3^2} \cr } } \right)$。

其中: σi2(i = 1，2，3)为第i 个随机效应参数方差; ρij(j = 1，2，3，i ≠ j)为第i 个随机效应与第j 个随机效应的协方差，满足ρij = ρji 。

1.3.5 误差项方差协方差(R)结构

在重复观测数据中，误差项的方差协方差矩阵R 可能存在明显异方差和自相关。为解决该问题，Davidian 等(1995)、Meng 等(2009)采用下式:

${R_{ij}} = {\sigma ^2}G_{ij}^{0.5}{\Gamma _{ij}}G_{ij}^{0.5}$ (7)
式中: σ2 为误差扩散的比例因子(Grégoire et al., 1995)，由模型的残差方差值所给定; Γij 为用来描述对象内误差自相关的nij × nij 维矩阵，本研究中由于各样地内观测数据间没有明显的相关性，故Γij 为单位矩阵; Gij 是用来描述对象间方差异质性的nij × nij 维对角矩阵，其中，对角元素为相应误差项的标准差。

本研究试图通过对残差方差增加权重消除异方差(Pinheiro et al., 2000; Calama et al., 2005)。从自变量为胸径的指数函数、幂函数和常数加幂函数3 个候选模型中由AIC和似然比检验确定一个效果最好的残差方差模型(Pinheiro et al., 2000)。

类型1: 指数函数

$\operatorname{var} \left( {{\varepsilon _{ijk}}} \right) = {\sigma ^2}\exp \left( {{2_\Upsilon }{D_{ijk}}} \right)$; (8)

类型2: 幂函数

$\operatorname{var} \left( {{\varepsilon _{ijk}}} \right) = {\sigma ^2}{D_{ijk}}^{2\Upsilon }$; (9)

类型3 常数加幂函数

$\operatorname{var} \left( {{\varepsilon _{ijk}}} \right) = {\sigma ^2}{\left( {{\Upsilon _1} + D_{ijk}^{\Upsilon 2}} \right)^2}$ (10)
式中: γ，γ1和γ2 为待估参数。

1.4 参数估计

本研究混合模型的计算是在S-Plus 软件nlme 函数上实现的，该函数中参数估计方法为LB 算法(Lindstrom et al., 1900)，主要包含2 个步骤: 惩罚最小二乘步(PNLS)和线性混合效应步(LME)，模型中所有待估参数通过这2 个步骤相互交替运算得到，详细计算见符利勇等(2012b)、Pinheiro 等(2000)。选用限制极大似然参数估计方法(restricted maximum likelihood，REML)(Yang et al., 2011)。

1.5 模型预测和评价

在利用考虑立地指数和立地指数与样地嵌套效应的嵌套2 水平非线性混合效应模型对冠幅进行预测时，需考虑以下2 种情形(Vonesh et al., 1997; Fang et al., 2001; Calama et al., 2005):

1)总体平均响应，又称固定效应响应，即预测冠幅时，只需在预测样地中测量模型中所含的林分变量和对象木胸高直径。

2)主体特定(subject-specific)响应，简称SS 响应，即预测冠幅时，除测量模型中所含自变量外，还需测量一定数量对象木的冠幅来估计随机效应参数(立地指数效应和立地指数与样地嵌套效应)。通常测量对象木的冠幅越多，模型预测精度越高(Yang et al., 2009)。为考虑测量成本和模型实用性，Calama 等(2005)建议随机测量4 株株对象木就能有效估计随机效应参数值，本研究采取该方法。

1.5.1 总体平均模型

总体平均模型(populationaveraged model，又称PA 模型)是指模型中形式参数只含固定效应部分，所有随机效应参数值默认为0(Yang et al., 2009)，即:

${\text{C}}{{\text{W}}_{ijk}} = f\left( {{v_{ijk}},{{\hat \phi }_{ij}}} \right)$ (11)
式中: CWijk和υijk 分别为第i 个立地指数等级第j 个样地中第k 株杉木的冠幅和自变量; ${\hat \phi _{ij}}$ 为形式参数，在PA 模型中，它只包含固定效应参数$\hat \beta $。

1.5.2 立地指数水平

假定最终模型中只考虑立地指数效应对冠幅的影响，而不考虑其他效应(如立地指数与样地的嵌套效应)，即公式(11)中 ${\phi _{ij}}$ 含有$\hat \beta $和${\hat u_i}$ 。通常${\hat u_i}$ 由下式(Vonesh et al., 1997)计算得到:

$\hat b \approx \hat G\hat C_i^T{\left( {{{\hat R}_i} + {{\hat C}_i}\hat G\hat C_i^T} \right)^{ - 1}}{\hat e_i}$。 (12)
式中:${\hat b_i} = {\hat u_i}$ 为立地指数所产生的q1 × 1 维随机效应; $\hat G = {\hat \psi _1}$ 为q1 × q1 维方差协方差矩阵; ${\hat C_i} = {\hat Z_i}$ 为 ni × q1 维设计矩阵; ni = $\sum\nolimits_{i = 1}^{{M_i}} {{n_{ij}}} $ 。

表 1 中，由于检验数据的区组与建模数据完全相同，因此不需重新计算${\hat u_i}$，预测时可直接取自最终模型参数的估计结果。

1.5.3 立地指数和样地嵌套2 水平(立地指数+立地指数* 样地)

当模型中同时考虑立地指数效应和立地指数与样地的嵌套效应对冠幅的影响时，公式(11)的 ${\phi _{ij}}$ 中除$\hat \beta $ 外还有ui和uij 。同样随机效应由公式(12)计算得出，此时，${\hat b_i} = {\left( {u_i^T,u_{i1}^T.u_{i2}^T, \cdots ,u_{i{M_i}}^T} \right)^T}$ 为(q1 + Miq2)× 1 维增广随机效应参数向量(Pinheiro et al., 2000)，$\hat G$ = diag(ψ1，ψ2，…，ψ2)为(q1 + Miq2)×(q1 + Miq2)维对角块正定矩阵;

$\eqalign{ {{\hat C}_i} = \left[ {\matrix{ {{Z_{i1}}} & {{E_{i1}}} & 0 & 0 & 0 \cr {{Z_{i2}}} & 0 & {{E_{i2}}} & 0 & 0 \cr \vdots & 0 & 0 & \ddots & 0 \cr {{Z_{i{M_i}}}} & 0 & 0 & 0 & {{E_{i{M_i}}}} \cr } } \right] & \cr {n_i} \times \left( {{q_1} + {M_{iq2}}} \right) \cr} $。
为设计矩阵。与只考虑立地指数效应相类似，表 1 中检验数据与建模数据有相同的立地指数等级，因此不需重新计算${\hat u_i}$ 。

1.5.4 模型评价

利用e，σ2，δ，R2和似然比检验对模型进行评价，其中指标e，σ2，δ 计算见公式(4)～(6)，似然比检验见1.3.3 节。

2 结果 2.1 基础模型

表 3 为模型(Ⅱ. 1)—模型(Ⅱ. 12)的评价指标。从表 3 中可看出，在建模数据和检验数据中，尽管所有模型指标较接近，但模型(Ⅱ. 10)(逻辑斯蒂模型)比其他模型预测效果稍好点，而且模型(Ⅱ. 10)在林分生长模型中也经常被用到(Huang et al., 2000; 李永慈等，2004)，因此本文选择它作为构建冠幅混合模型的基础模型:

${\text{C}}{{\text{W}}_{ijk}} = {\phi _1}/\left[ {1 + {\phi _2}\exp \left( { - {\phi _3}{D_{ijk}}} \right)} \right] + {\varepsilon _{ijk}}$ (13)
式中: CWijk和Dijk 分别为立地指数第i 等级中第j 个样地第k 株对象木冠幅(m)和胸高直径(cm);${{\phi _1}}$，${{\phi _2}}$和${{\phi _3}}$ 为形式参数。

表3 模型评价指标 Tab.3 Models evaluation indexes
2.2 林分变量

为避免模型中过多参数和变量间共线性，将选择与冠幅相关性较大的样地优势木平均高(DH)、 对象木冠底高(HCB)和对象木树高(H)作为新增加的林分变量，模型表达式为:

${\text{C}}{{\text{W}}_{ijk}} = \left( {{\phi _1} + {\phi _4}{\text{D}}{{\text{H}}_{ij}}} \right)/\left\{ {1 + \left( {{\phi _2} + {\phi _5}{\text{HC}}{{\text{B}}_{ijk}}} \right) \\ \exp \left[ { - \left( {{\phi _3} + {\phi _6}{H_{ijk}}} \right){D_{ijk}}} \right]} \right\} + {\varepsilon _{ijk}}$ (14)
式中: DHij 为立地指数第i 等级中第j 个样地的优势木平均高(m); CHijk和Hijk 分别为第i 等级中第j 个样地第k 株对象木冠底高(cm)和树高(m);${{\phi _4}}$，${{\phi _5}}$和${{\phi _6}}$ 为形式参数。

2.3 混合模型构造

当同时考虑立地指数效应和立地指数与样地嵌套效应时，共有63 种不同随机效应组合形式，其中 12 种形式计算收敛，当立地指数效应和立地指数与样地的嵌套效应同时作用在${{\phi _3}}$和${{\phi _5}}$ 上时，AIC = 2 714. 64最小，Log lik = － 1 344. 32 最大，模型表达式为:

$\eqalign{ & {\rm{C}}{{\rm{W}}_{ijk}} = \left( {{\beta _1} + {\beta _4}{\rm{D}}{{\rm{H}}_{ijk}}} \right)/\left\{ {1 + } \right. \cr & \left[ {{\beta _2} + \left( {{\beta _5} + {u_{5i}} + {u_{5ij}}} \right){\rm{HC}}{{\rm{B}}_{ijk}}} \right] \cr & \left. {\exp \left[ { - \left( {{\beta _3} + {u_{3i}} + {u_{3ij}} + {\beta _6}{H_{ijk}}} \right){D_{ijk}}} \right]} \right\} + {\varepsilon _{ijk}} \cr} $。 (15)
式中: β1 ～ β6 为固定效应参数; u3i和u5i 分别为立地指数作用在 3和5 上的随机效应参数; u3ij和u5ij 分别为样地作用在 3和5 上的随机效应参数。

2.4 误差项方差协方差(R)结构

表 4 为模型(15)对应3 种加权残差方差模型和不加权(独立等方差)时模型的评价指标。从表 4 中可知，考虑残差加权的3 种模型与不加权模型差异显著(P ＜ 0. 001)，表明3 种加权残差方差模型能明显解除异方差。其中，幂函数［模型(9)］的指标最小，故选它为模型(15)的残差方差模型。

表4 各残差方差模型评价指标 Tab.4 Evaluation indexes for each residual variance model
2.5 模型参数估计

表 5 给出了模型(13)、模型(14)和模型(15)的参数估计值以及评价指标(AIC和Loglik)。模型(13)和模型(14)未考虑随机效应和对残差方差加权，故方差参数只有σ2 。模型(15)的评价指标比另外2 个模型明显要好，说明立地指数以及立地指数和样地的嵌套效应对冠幅影响较大。把固定效应参数估计值代入到模型(15)中，得到杉木冠幅的一般模型表达式为:

$\eqalign{ & {\text{C}}{{\text{W}}_{ijk}} = \left( {7.1959 - 0.0334{\text{D}}{{\text{H}}_{ijk}}} \right)/\left\{ {1 + } \right. \cr & \left[ {2.9064 + \left( { - 0.0954 + {u_{5i}} + {u_{5ij}}} \right){\text{HC}}{{\text{B}}_{ijk}}} \right] \cr & \exp \left[ { - \left( {0.0417 + {u_{3i}} + {u_{3ij}} + } \right.} \right. \cr & \left. {\left. {\left. {0.0008{H_{ijk}}} \right){D_{ijk}}} \right]} \right\} + {\varepsilon _{ijk}} \cr} $。
其中，${u_i} = \left[ {\matrix{ {{u_{3i}}} \cr {{u_{5i}}} \cr } } \right] \sim N\left. {\left\{ {\left[ {\matrix{ 0 \cr 0 \cr } } \right]} \right.,{\psi _1} = \left( {\matrix{ 0 & 1 \cr 1 & {0.0248} \cr } } \right)} \right\}$,${u_{ij}} = \left[ {\matrix{ {{u_{3ij}}} \cr {{u_{5ij}}} \cr } } \right] \sim N\left\{ {\left[ {\matrix{ 0 \cr 0 \cr } } \right],{\psi _2} = \left( {\matrix{ {0.0225} & {0.532} \cr {0.532} & {0.0944} \cr } } \right)} \right\}$,${\varepsilon _{ij}} \sim N\left( {0,{R_{ij}} = 0.093G_{ij}^{0.5}{I_{{n_i}}}G_{ij}^{0.5}} \right),\operatorname{var} \left( {{\varepsilon _{ijk}}} \right) = 0.093D_{ijk}^{1.126}$。

2.6 模型预测和评价

表 6 列出模型(15)对应的总体平均水平(PA)、 立地指数水平(SI)以及同时考虑立地指数和立地指数与样地的嵌套效应(SI + SI* Plot，简称嵌套2 水平)的评价指标。为与混合模型比较，表 6 还给出了模型(13)和模型(14)对应的评价指标。从表 6 中可知，嵌套2 水平预测效果最好，其次是SI 水平，而PA 水平预测效果最差。3 种水平的平均预测残差(e)都显著地不等于0(α = 0. 05)。

与模型(13)和模型(14)相比，模型(15)的嵌套 2 水平(SI + SI* Plot)明显提高了模型预测精度。 例如，在建模数据中，对于R2，模型(15)的嵌套2 水平比基础模型(13)提高了111. 52%，比基础模型(14)提高了81. 55%。在检验数据中，对于δ，模型(15)的嵌套2 水平比基础模型(13)减少了 42. 77%，比基础模型(14)减少了39. 80%。而模型(15)的PA 水平和SI 水平与模型(13)和模型(14)预测效果较接近，说明立地指数和样地的嵌套效应对冠幅的随机效应较大。

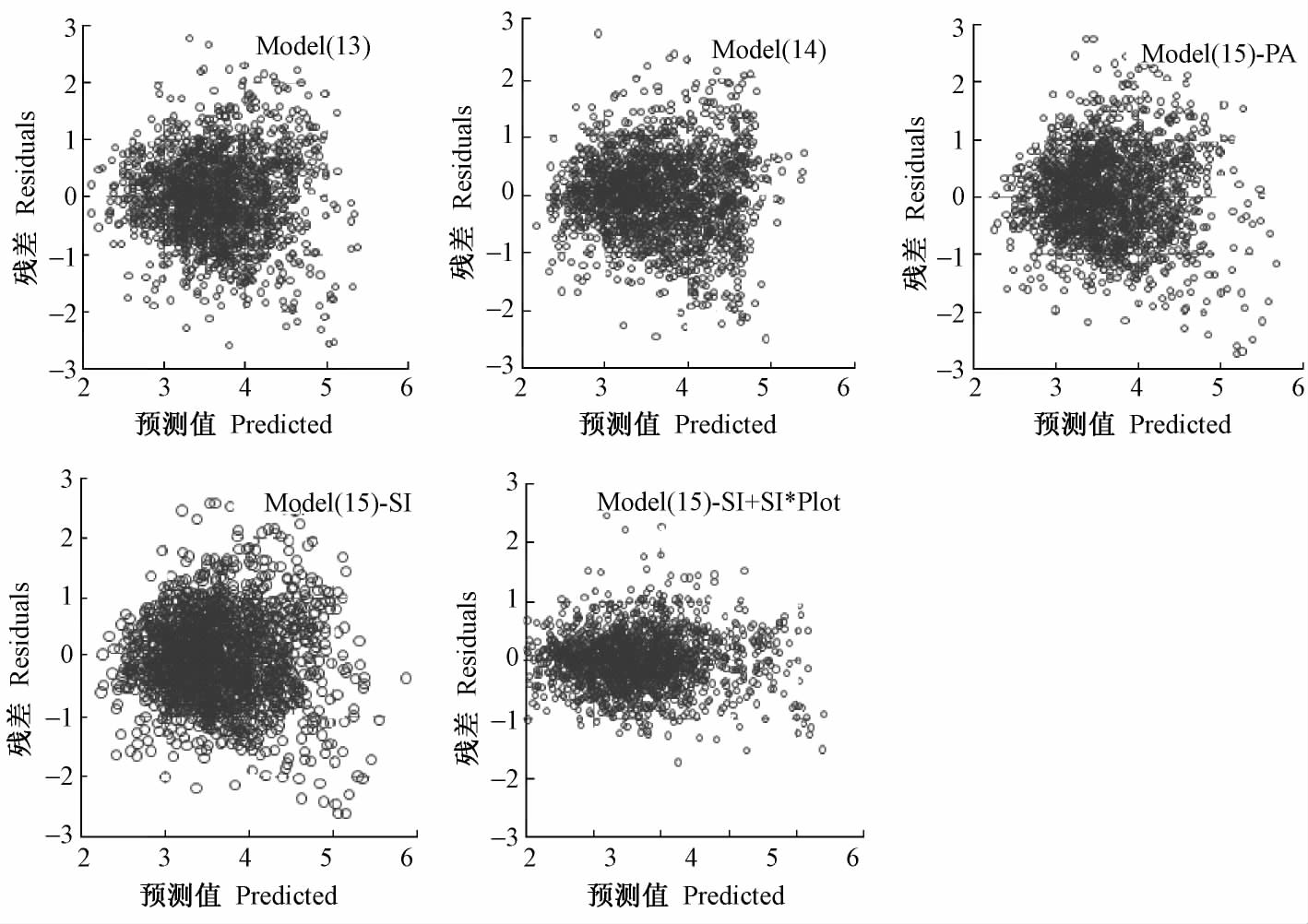
图 1 为模型(15)对应的PA 水平、SI 水平、SI + SI* Plot 水平以及模型(13)和模型(14)拟合建模数据的残差分布图。从图 1 中可知，模型(13)和模型(14)的残差呈喇叭分布，即存在异方差，而模型(15)的SI + SI* Plot 水平残差分布比其他模型明显紧密且平行于横坐标。同时通过图 1 还能说明残差方差加权不能明显消除模型(15)的PA 水平和SI 水平的异方差。对于检验数据，各模型残差分布与建模数据相类似，本研究不再给出。

图1 各模型残差分布 Fig.1 Residuals distribution for each model

综合以上分析，把同时考虑立地指数效应和立地指数与样地嵌套效应的模型(15)作为预测杉木冠幅大小的最终模型。

3 结论与讨论

与Calama 等(2005)的做法一样，首先从常见林分模型中确定一个较好描述冠幅和胸高直径关系的模型作为基础模型。关于模型中形式参数是否包含随机效应，Calama 等(2005)是在考虑各形式参数是否包含林分变量之前确定，但通常由于模型增加林分变量后将新增加部分形式参数，这些形式参数可能受随机效应因子的影响。基于该问题，本研究首先在基础模型中增加林分变量，然后在增加林分变量的模型中确定各形式参数是否考虑随机效应。如果按照Calama 等(2005)方法，本实例最终选择的最佳混合模型为:

$\eqalign{ & {\text{C}}{{\text{W}}_{ijk}} = \left( {{\beta _1} + {\beta _4}{\text{D}}{{\text{H}}_{ijk}}} \right)/\left\{ {1 + \left( {{\beta _2} + {\beta _5}{\text{HC}}{{\text{B}}_{ijk}}} \right)} \right. \cr & \left. {\exp \left[ { - \left( {{\beta _3} + {u_i} + {u_{ij}} + {\beta _6}{H_{ijk}}} \right){D_{ijk}}} \right]} \right\} + {\varepsilon _{ijk}} \cr} $， (16)
即，增加的林分变量对应的形式参数，如 4，5和6 不考虑随机效应，故 4 = β4，5 = β5，6 = β6 只含固定效应部分，而之前基础模型(13)中的 1和2 不考虑随机效应参数，3 考虑立地指数效应和立地指数与样地的嵌套效应。模型(16)的参数估计量见表 5，对应的建模数据和检验数据评价指标见表 6。模型(15)的AIC 比模型(16)要小，Loglik 比模型(16)要大，通过似然比检验2 个模型差异显著(P ＜ 0. 000 1)。同时预测指标e，ξ，δ，R2 都满足模型(15)比模型(16)要好，因此说明本研究所使用的方法比Calama 等(2005)要好。

表5 各模型参数估计值和评价指标① Tab.5 Parameter estimates and evaluation indexes for each model

表6 各模型评价指标 Tab.6 Evaluation indexes for each model

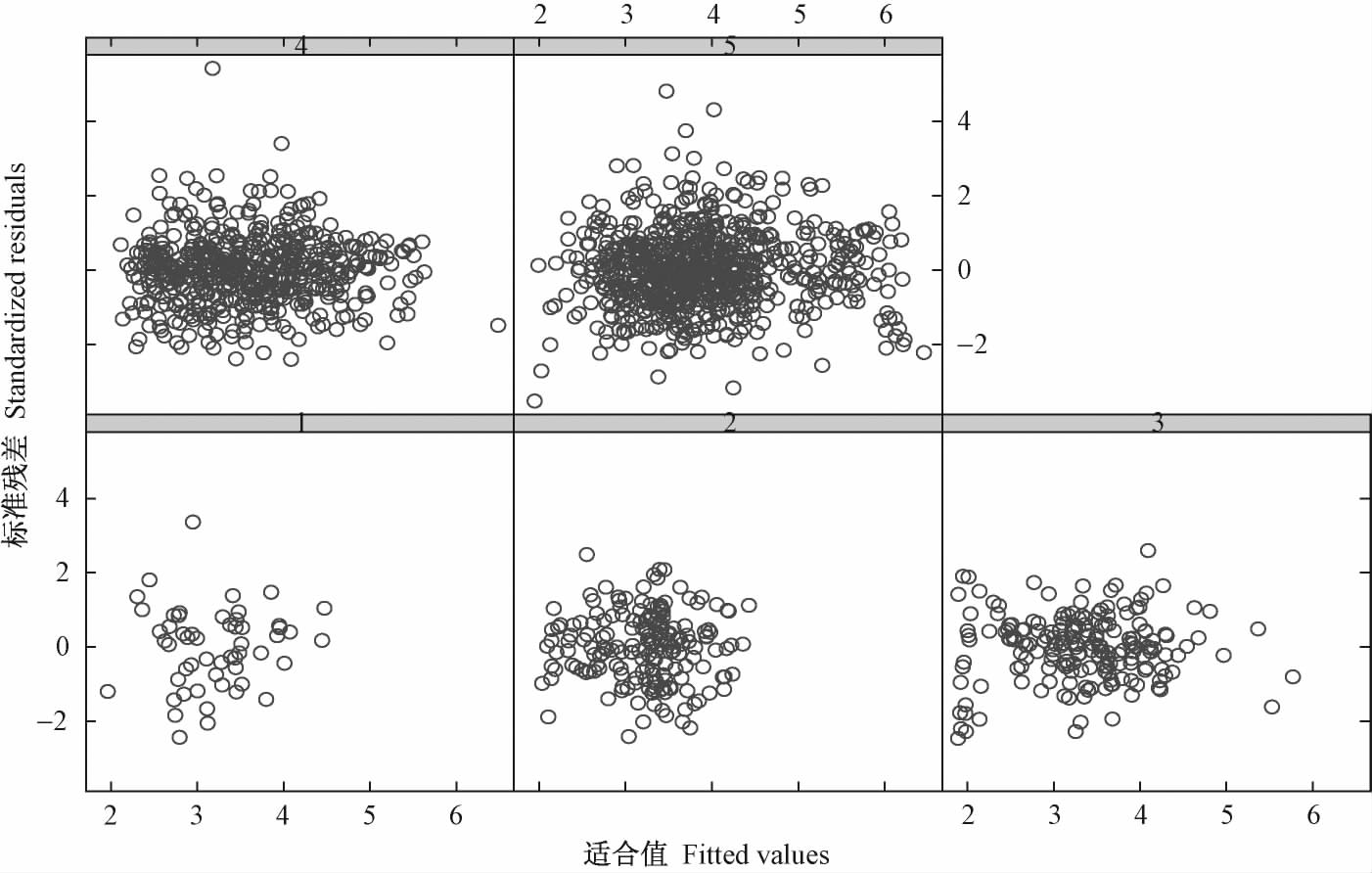
为改进模型预测精度，除胸高直径外，本研究还考虑17 个林分和树木因子对冠幅的影响。研究发现对象木树高、冠底高和优势木平均高对冠幅影响最大。3 个指标中，优势木平均高为样地水平，剩下 2 个为单木水平。尽管模型中增加优势木平均高能减少各样地间随机效应差异(Pinheiro et al., 1998; Calama et al., 2005; Yang et al., 2009)，但模型(15)的SI 水平和SI + SI* plot 水平预测效果差异较大(表 6)，表明在模型(15)中再增加样地水平变量能进一步提高模型预测精度。林分郁闭度(canopy density，简称CD)是除被选中的3 个指标外对冠幅影响最大的一个样地水平变量。把样地按CD ＜ 0. 5，0. 5≤CD ＜ 0. 6，0 . 6≤CD ＜ 0. 7，0. 7≤CD ＜ 0. 8和CD≥0. 8 划为5 个等级，构造哑变量K，其中 K1 = 1 表示郁闭度第1 个等级，K1 = 0 为剩下其他等级，K2 = 1 表示郁闭度第2 个等级，K2 = 0 为剩下其他等级，依次类推，其中K1 = K2 = K3 = K4 = 0 时表示郁闭度第5 个等级(Calama et al., 2005)。 假定把哑变量K 作用在形式参数φ1 上，模型写为:

$\eqalign{ & {\text{C}}{{\text{W}}_{ijk}} = \left( {{\beta _1} + \beta _1^{\left( 1 \right)}{K_1} + \beta _1^{\left( 2 \right)}{K_2} + \beta _1^{\left( 3 \right)}{K_3} + \beta _1^{\left( 4 \right)}{K_4} + } \right. \cr & \left. {{\beta _4}{\text{D}}{{\text{H}}_{ijk}}} \right)/\left\{ {1 + \left[ {{\beta _2} + \left( {{\beta _5} + {u_i} + {u_{ij}}} \right){\text{HC}}{{\text{B}}_{ijk}}} \right]} \right. \cr & \left. {\exp \left[ { - \left( {{\beta _3} + {u_i} + {u_{ij}} + {\beta _6}{H_{ijk}}} \right){D_{ijk}}} \right]} \right\} + {\varepsilon _{ijk}} \cr} $。 (17)
模型中其他变量与模型(15)完全相同。通过对模型(17)进行计算，参数估计量、AIC和Loglik 见表 5，对应建模数据和检验数据的评价指标见表 6。从 表 5和表 6 可知，模型(17)在模型(15)的基础上能进一步提高预测精度。图 2 为模型(17)拟合建模数据时各等级的残差分布图。同样模型(15)还可增加其他样地水平变量提高模型预测精度。需注意的是模型中过多参数可能会影响模型计算不收敛，与此同时模型中林分变量过多会增加野外调查成本，从而限制模型应用(Pinheiro et al., 2000; Calama et al., 2005; Ademe et al., 2008)。本研究基于这些问题，最终只选择包含胸高直径在内的4 个主要林分变量。

图2 模型( 17) 对应5 个不同郁闭度等级的残差分布 Fig.2 Residuals distribution of 5 different canopy density grades for model ( 17)

利用模型(15)对冠幅进行预测时，最关键的步骤是对随机效应参数估计(Fang et al., 2001; Calama et al., 2005)。应用时，除调查模型中含有的林分变量外，还需在样地中测量一定株树的冠幅来估算立地指数效应和立地指数与样地的嵌套效应。 Calama 等(2005) 和Yang 等(2009)对需抽取多少株树木计算随机效应最合适进行详细研究。Yang 等(2009)建议估计随机效应参数时所调查的树木株树越多越好，但这需根据实际情况而定。目前较常用的是在所预测样地的子样地中随机抽取4 株树木估计随机效应(Calama et al., 2005)，本研究进一步验证该方法可行。本文主要为方法研究，除杉木树种外，其他树种都可以利用相似方法来构建冠幅模型。

参考文献(References)
[1] 杜纪山, 唐守正,王洪良.2000. 天然林区小班森林资源数据的更新模型.林业科学, 36(2): 26-32.(1)
[2] 符利勇, 李永慈, 李春明, 等. 2012a. 利用2种非线性混合效应模型(2水平)对杉木林胸径生长量的分析. 林业科学, 48(5):36-43.(1)
[3] 符利勇, 唐守正.2012b. 基于非线性混合模型的杉木优势木平均高. 林业科学, 48 (7): 66-71.(1)
[4] 雷相东, 张则路, 陈晓光. 2006. 长白落叶松等几个树种冠幅预测模型的研究. 北京林业大学学报, 28(6): 75-79.(2)
[5] 李永慈,唐守正.2004. 用Mixed和Nlmixed过程建立混合生长模型.林业科学研究, 17(3): 297-283.(1)
[6] Ademe P, del Río D, Caellas I. 2008. Amixed nonlinear height-diameter model for Pyrenean oak (Quercus pyrenaica Willd.). Forest Ecology and Management, 256(1/2): 88-98.(1)
[7] Bechtold W A. 2004. Largest crown-width prediction models for 53 species in the western United States. Western Journal of Applied Forestry, 19(4): 245-250.(1)
[8] Biging G S, Dobbertin M. 1995. Evaluation of competition indices in individual tree growth models. Forest Science, 41 (2): 360-377.(1)
[9] Biging G S, Dobbertin M. 1992. A comparison of distance-dependent competition measures for height and basal area growth of individual conifer trees. Forest Science, 38(3): 695-720.(1)
[10] Calama R, Montero G. 2005. Multilevel linear mixed model for tree diameter increment in stone pine (Pinus pinea): a calibrating approach. Sliva Fennica, 39(1): 37-54.(12)
[11] Calama R, Montero G. 2004. Interregional nonlinear height-diameter model with random coefficients for stone pine in Spain. Canadian Journal of Forest Research, 34(1): 150-163.(2)
[12] Davidian M, Giltinan D M. 1995. Nonlinear models for repeated measurement data. Chapman& Hall, New York.(1)
[13] Fang Z, Bailey R L. 2001. Nonlinear mixed effects modeling for slash pine dominant height growth following intensive silvicultural treatments. Forest Science, 47(3): 287-300.(3)
[14] Garrett M F, Laird N M, Ware J H. 2004. Applied longitudinal analysis. Wiley-Interscience, John Wiley and Sons, Inc., Publication, New Jersey.(1)
[15] Gill S J, Biging G S, Murphy A C. 2000. Modeling conifer tree crown radius and est imating canopy cover. Forest Ecology and Management, 126(3): 405-416.(1)
[16] Grégoire T G, Schabenberger O, Barrett J P. 1995. Linear modeling of irregularly spaced, unbalanced, longitudinal data from permanent plot measurements. Canadian Journal of Forest Research, 25(1): 137-156.(1)
[17] Huang S, Price D, Titus S J. 2000. Development of ecoregion-based height-diameter models for white spruce in boreal forests. Forest Ecology and Management, 129(1/3): 125-141.(1)
[18] Keselman H J, Algina J, Kowalchuk R K, et al. 1999. A comparison of recent approaches to the analysis of repeated measurements. Br J Math Stat Psychol, 52(1): 63-78.(1)
[19] Lindstrom M J, Bates D M. 1990. Nonlinear mixed effects models for repeated measures data. Biometrics, 46(3): 673-687.(1)
[20] Meng S X, Huang S. 2009. Improved calibration of nonlinear mixed-effects models demonstrated on a height growth function. Forest Science, 55(3): 239-248.(1)
[21] Monleon V J, Azuma D, Gedney D. 2004. Equations for predicting uncompacted crown ratio based on compacted crown ratio and tree attributes. Western Journal of Applied Forestry, 19(4): 260-267.(1)
[22] Monserud R A, Sterba H. 1996. A basal area increment model for individual trees growing in even-and uneven-aged forest stands in Austria. Forest Ecology and Management, 80(1/3): 57-80.(2)
[23] Pinherio J C, Bates D M. 1998. Model building for nonlinear mixed effects model. Deparment of Statistics, University of Wisconsin, Madison, Wis.(2)
[24] Pinherio J C, Bates D M. 2000. Mixed-effects models in S and S-PLUS. Spring-Verlag, New York, NY.(6)
[25] Russell M B, Weiskittel A R.2011. Maximum and largest crown width equations for 15 tree species in Maine. Western Journal of Applied Forestry, 28(2): 84-91.(1)
[26] Sánchez-González M, Caellas I, Montero G. 2008. Generalized height-diameter and crown diameter prediction models for cork oak forests in Spain. Forest Systems, 16(1): 76-88.(8)
[27] Sönme T. 2009. Diamater at breast height-crown diameter prediction models for Picea orientalis. African Journal of Agricultural Research, 4(3): 215-219.(4)
[28] Spurr S H, Barnes B V. 1980. Forest ecology.3rd edn. John Wiley, New York, 527.(2)
[29] Toney C, Reeves M C. 2009. Equations to convert compacted crown ratio to uncompacted crown ratio for trees in the interio west. Western Journal of Applied Forestry, 24(2): 76-82.(1)
[30] Uzoh F C C, Oliver W W. 2008. Individual tree diameter increment model for managed even-aged stands of ponderosa pine throughout the western United States using a multilevel linear mixed effects model. Forest Ecology and Management, 256(3): 438-445.(5)
[31] Vonesh E F, Chinchilli V M. 1997. Linear and nonlinear models for the analysis of repeated measurements. Marcel Dekker, New York.(2)
[32] Wykoff W R. 1990. A basal area increment model for individual conifers in the Northern Rocky Mountains. Forest Science,36(4): 1077-1104.(2)
[33] Yang Y, Huang S. 2011.Comparison of different methods for fitting nonlinear mixed forest models and for making predictions. Canadian Journal of Forest Research, 41(8): 1671-1686.(2)
[34] YangY, Huang S, Meng S X, et al. 2009. A multilevel individual tree basal area increment model for aspen in boreal mixedwood stands. Canadian Journal of Forest Research, 39(11): 2203-2214.(4)