林业科学  2013, Vol. 49 Issue (8): 58-64   PDF    
DOI: 10.11707/j.1001-7488.20130809
0

文章信息

刘志理, 戚玉娇, 金光泽
Liu Zhili, Qi Yujiao, Jin Guangze
小兴安岭谷地云冷杉林叶面积指数的季节动态及空间格局
Seasonality and Spatial Pattern of Leaf Area Index of a Spruce-Fir Forest at the Valley in Xiaoxing’an Mountains
林业科学, 2013, 49(8): 58-64
Scientia Silvae Sinicae, 2013, 49(8): 58-64.
DOI: 10.11707/j.1001-7488.20130809

文章历史

收稿日期：2012-8-6
修回日期：2013-3-25

作者相关文章

刘志理
戚玉娇
金光泽

引用本文
刘志理, 戚玉娇, 金光泽. 2013. 小兴安岭谷地云冷杉林叶面积指数的季节动态及空间格局[J]. 林业科学, 49(8): 58-64.
Liu Zhili, Qi Yujiao, Jin Guangze. 2013. Seasonality and Spatial Pattern of Leaf Area Index of a Spruce-Fir Forest at the Valley in Xiaoxing’an Mountains. Scientia Silvae Sinicae, 49(8): 58-64.  DOI: 10.11707/j.1001-7488.20130809
小兴安岭谷地云冷杉林叶面积指数的季节动态及空间格局
刘志理1, 戚玉娇2, 金光泽1    
1. 东北林业大学生态研究中心 哈尔滨 150040;
2. 东北林业大学林学院 哈尔滨 150040
收稿日期：2012-8-6；修回日期：2013-3-25
基金项目：国家"十二五"科技支撑计划(2011BAD37B01); 长江学者和创新团队发展计划(IRT1054)。
通讯作者：金光泽
摘要：应用半球摄影技术对小兴安岭谷地云冷杉林落叶季节(7—11月)的有效叶面积指数进行动态监测。为准确估测谷地云冷杉林的叶面积指数(LAI), 对叶凋落末期(11月初)的有效叶面积指数(LAIe)进行木质部分及集聚效应(包括冠层水平集聚和针簇内集聚效应)的合理校正, 以校正值作为该时期常绿树种的真实叶面积指数(LAIt), 结合凋落物法, 反推得到LAIt的季节动态并分析LAIt最大时期(7月)和最小时期(11月)的空间格局特征。结果表明: 谷地云冷杉林11月初木质部分所占比例(α)均值为0.10±0.06, 冠层水平集聚指数(ΩE)均值为0.90±0.04, 常绿针叶树种的针簇内集聚指数(针簇比, γE)为红松(1.77)>云杉(1.28)>冷杉(1.10); LAIt随季节变化呈递减趋势,7月达到峰值(3.97), 11月值最小(2.71); 相对而言, 光学仪器法测定的LAIe各调查期的低估范围为28.81%~43.24%, 平均低估值为32.98%; 变异函数分析表明, LAIt大的月份其空间异质性程度也大, 7和11月LAIt的空间异质性主要由空间自相关引起, 其引起的空间异质性分别占总空间异质性的99.8%,66.9%。
关键词： 小兴安岭    谷地云冷杉林    有效叶面积指数    叶面积指数    校正    凋落物法    
Seasonality and Spatial Pattern of Leaf Area Index of a Spruce-Fir Forest at the Valley in Xiaoxing’an Mountains
Liu Zhili1, Qi Yujiao2, Jin Guangze1    
1. Center for Ecological Research, Northeast Forestry University Harbin 150040;
2. School of Forestry, Northeast Forestry University Harbin 150040
Abstract: Leaf area index (LAI) is one of the most frequently used parameters for analysis of canopy structure. We monitored the seasonality of effective leaf area index (LAIe) for a Spruce-fir forest at the valley in Xiaoxing'an Mountains by using Digital Hemispherical Photography (DHP) during deciduous season (from July to November). In order to estimate LAI more accurate for the stand, the optically-based effective leaf area index (LAIe) values of early November were adjusted to eliminate wood elements and clumping effects (including both beyond and within shoots). The adjusted value was regarded as true leaf area index (LAIt) of evergreen species. The seasonal dynamics of LAIt were obtained by incorporation of litterfall data for each observation, and we analyzed spatial pattern of LAIt during the maximum and minimum LAIt period. Results showed that the mean woody-to-total area ratio (α) was 0.10±0.06 and the mean clumping effect (ΩE) was 0.90±0.04 in early November for Spruce-fir forest at the valley, and the order of mean needle-to-shoot area ratio (γE) for evergreen coniferous species was Pinus koraiensis (1.77)>Picea spp. (1.28)>Abies nephrolepis (1.10). LAIt decreased with season from July to November, and LAIt was highest with a value of 3.97 in July, and lowest in November with a value of 2.71. In comparison with LAIt , LAIe was underestimated by 32.98% (from 28.81% to 43.24%); The spatial heterogeneity of the LAIt was greater with the higher LAIt, and the spatial heterogeneity of LAIt for July and November resulted mainly from the spatial autocorrelation that accounted for 99.8% and 66.9% of the total space heterogeneity, respectively.
Key words: Xiaoxing&rsquo    an Mountains    spruce-fir forest at valley    effective leaf area index    leaf area index    calibration    litterfall method    

叶面积指数(leaf area index，LAI)是描述森林冠层结构的重要指标之一(Muraoka et al., 2010)，被定义为单位地面面积上总绿叶面积的一半(Chen et al., 1992)，它控制着冠层与大气间物质能量的交换(Sonnentag et al., 2007; Sprintsin et al., 2007; Behera et al., 2010)。LAI 广泛应用于碳、水循环的模拟(Asner et al., 2003; Thimonier et al., 2010)、净初级生产力及总初级生产力的估算(李文华等，1997; Barr et al., 2004)等方面。此外，准确测量 LAI 对实现研究尺度从叶片转换到冠层结构具有重要意义(Gower et al., 1991)。

LAI 的地面测量方法通常分为直接法和间接法(Deblonde et al., 1994; Jonckheere et al., 2004; Pinto-Júnior et al., 2011)。直接法估测LAI 相对准确，但因其费时、费力，且具有一定破坏性，故只能在小尺度范围内应用，不适合长期的LAI 时空动态变化监测(Marshall et al., 1986; Bréda，2003; Macfarlane et al., 2007; Pueschel et al., 2012)。相对而言，间接法(光学仪器法)能快速简便地估测LAI及其季节动态(Wasseige et al., 2003)，但该方法基于林冠内叶元素的随机分布; 而大部分树种的叶元素并非随机分布，其分布方式与林冠和树枝的分布密切相关(Chen et al., 1997)，植被冠层在多个尺度内的集聚现象以及树干、树枝等木质部分的影响都应考虑，因此，光学仪器测定值并非真实叶面积指数(true leaf area index，LAIt)，而被称作有效叶面积指数(effective leaf area index，LAIe)(Weiss et al., 2004)。在众多间接法中，半球摄影技术(digital hemispherical photography，DHP)被广泛应用于估测地面水平上的LAI，该方法易于实施、可测定更多的林冠结构参数且能永久存档、能够量化集聚效应，且相对于其他光学仪器造价低(Coops et al., 2004;Chen et al., 2006; Pueschel et al., 2012)。

云冷杉林(spruce-fir forest)是我国寒温性常绿针叶林中分布最广的森林类型(李文华，1980)，小兴安岭谷地云冷杉林是本地区非地带性顶极植被，其面积和蓄积量分别占小兴安岭地区天然林总面积和蓄积量的20%和23%，不仅提供大量木材，且在水源涵养和风景游憩等方面也起重要作用(黑龙江森林编辑委员会，1993)。Luo 等(1997)估测了贡嘎山地区不同海拔云冷杉林的最大LAI; 吕瑜良等(2007)应用LAI-2000 植物冠层分析仪比较4 种岷江冷杉林分生长季节LAI 的差异性，并分析LAI 与海拔和坡向的关系。以往研究对于常绿针叶林多采用光学仪器法或是经过参数校正(用于校正集聚效应及木质部分)来获得LAI 及其季节动态，但校正参数随研究区域内叶子的凋落而存在差异(尤其是落叶树种所占比例越大，差异越明显)，因此，只利用校正光学仪器法并不适于测定小兴安岭地区谷地云冷杉林(落叶树种相对优势度为32. 8%)LAI 的季节动态。本研究通过结合光学仪器法和凋落物法，探讨小兴安岭谷地云冷杉林LAIt的季节动态(7—11 月)，以LAIt为参考值，对比与LAIe的差异性，并分析LAIt的空间格局特征，以期为提高光学仪器法估测谷地云冷杉林LAI 的准确性提供科学依据，为该区域的生态过程模拟提供高精度参数。

1 材料与方法 1.1 研究区概况

野外调查在黑龙江省凉水国家级自然保护区(47°10'50″ N、128°53'20″ E)进行，保护区位于黑龙江省伊春市带岭区，属小兴安岭南部达里带岭支脉的东坡。地形比较复杂，最高山脉海拔707. 3 m。该区属于温带大陆性季风气候，年均气温 － 0. 3 ℃，年均最高气温7. 5 ℃，年均最低气温 － 6. 6 ℃。多年平均降水量676 mm，降水多集中在 7 月。年积雪期130 ～ 150 天，年无霜期100 ～ 120天。本研究区域的谷地云冷杉林是谷地云冷杉林天然分布的南界，是全球气候变化的敏感地区，地势平缓，土壤为隐地带性的沼泽土，且有永冻土层分布，上层林木以云杉(Picea spp.)和冷杉(Abies nephrolepis)为主，林分年龄一般为60 ～ 80 年，胸径20 ～ 25 cm，高15 ～ 20 m。

1.2 研究方法 1.2.1 样点设置与数据采集

野外调查在2006 年设置的谷地云冷杉林60 m × 60 m 样地内进行(基本概况见表 1)。随机布设20 个样点，各样点布设1 个凋落物收集器，凋落物收集器用径粗8 mm 的铁丝和尼龙网围成(孔径1 mm，深0. 5 ～ 0. 6 m)，网口正方形，面积1. 0 m2，凋落网底离地面0. 5 m;各凋落物收集器旁用三根长30 cm 的PVC 管固定光学仪器采集数据的位置。使用Winscanopy2006冠层分析仪(Regent，Instruments Inc.，Quebec，Canada; 由Nikon Coolpix4500和180° 鱼眼镜头组成)在各样点采集半球摄影图像，用三脚架固定鱼眼镜头且离地面1. 3 m，为避免阳光直射，选在阴天或日出、日落前后进行，摄像时曝光及快门均设置自动状态，采集时间为2010 年7 月1 日、8 月1日、9 月1 日、9 月15 日、10 月1 日、10 月15 日及11月1 日。凋落物的收集与半球摄影法的图像采集同步进行，将凋落叶按树种分类，分别称质量后，即时将样品在65 ℃ 下烘干至恒质量，测其干质量，结合各树种的比叶面积(specific leaf area，SLA)，得到各样点各时期凋落物产生的LAI。本研究中主要树种的比叶面积参照Liu 等(2012)的研究方法测定。

表1 小兴安岭谷地云冷杉林树种组成及其比叶面积① Tab.1 Species composition and specific leaf area for the spruce-fir forest at valley in Xiaoxing'an Mountains
1.2.2 试验原理

谷地云冷杉林存在较大比例落叶树种，本研究将常绿树种和落叶树种分开处理，首先利用光学仪器法测定11 月初LAIe，该时期落叶树种凋落完毕，该林型可看做常绿针叶林，将该时期的LAIe进行校正后作为LAIt，再结合凋落物法得到LAIt的季节动态(7—11 月)。为获得11 月初相对准确的LAIt，对光学仪器测得的LAIe进行校正中考虑木质部分以及集聚效应，其中集聚效应体现在冠层水平及针簇水平上，根据前人的理论和验证(Leblanc et al., 2001)，LAIt计算公式如下:

$$L = (1 - \alpha ){L_{\text{e}}}\frac{{{\gamma _{\text{E}}}}}{{{\Omega _{\text{E}}}}}$$ (1)
式中: L 为真实叶面积指数; Le为有效叶面积指数; α 为木质部分面积占总面积的比率; ΩE为冠层水平的集聚指数; γE是针叶面积与簇面积的比率(针簇水平上的集聚指数)，谷地云冷杉林样地内常绿针叶树种云杉、冷杉及红松的γE参照Liu 等(2012)的研究方法测定，再根据3 树种的胸高断面积比例进行加权得到整个林分11 月初的γE。

由式(1)得到11 月1 日的LAIt，加上11 月1日收集的凋落物产生的LAI，得到10 月15 日的LAIt，以此类推，得到小兴安岭谷地云冷杉林7—11 月各调查时期的LAIt。

1.2.3 数据处理

利用Photoshop CS 8. 01(Adobe Systems Inc，USA)软件参照Qi 等(2012)的方法消除11 月1 日半球摄影图像中树干等木质部分产生的影响。半球摄影图像采用DHP 软件进行处理，处理时提取0 ～ 60°天顶角范围内的LAI。冠层上的集聚采用DHP-TRACWin 软件(Leblanc et al., 2005; Macfarlane et al., 2007)计算的ΩE值校正，选用40 ～45°天顶角测定ΩE。LAI 的空间异质性用变异函数的主要参数块金值、基台值、尺度、空间结构比等来反映，参数使用GS + 7. 0(Gamma Design Software，2004)来计算。

2 结果与分析 2.1 校正参数α，ΩE及γE的获取

11 月初木质部分产生的误差为0. 04 ～ 0. 22(表 2)，均值为0. 10 ± 0. 06，表明此时常绿树种产生的LAIt最大(占光学仪器测定值的90%); 各样点冠层水平上的集聚效应差异较小(最大值与最小值相差 15%)，均值为0. 90 ± 0. 04，表明谷地云冷杉林在 11 月初冠层水平上不存在明显集聚效应。总体来看，常绿针叶树种γE的排列顺序为红松(1. 77)＞云杉(1. 28)＞ 冷杉(1. 10)，不同树种的γE均随林冠高度的降低而减小(表 3)，表明γE受树木在整个林分冠层中位置的影响。

表2 11 月各样点木质部分所占比例( α) 和集聚指数( ΩE ) 统计( n = 20) Tab.2 The woody-to-total area ratio and clumping index in November( n = 20)

表3 小兴安岭谷地云冷杉林常绿针叶树种的针簇比( γE ) ① Tab.3 γE for evergreen coniferous species in the spruce-fir forest at valley in Xiaoxing'an Mountains
2.2 凋落物量动态

谷地云冷杉林主要组成树种的叶凋落物有明显差异(图 1)。白桦存在2 个落叶高峰期，而云冷杉、兴安落叶松及其他树种均存在1 个落叶高峰期。白桦最先在8 月达到第1 个落叶高峰，第2 个高峰出现在9 月下半月，且凋落基本完毕(10 月以前叶凋落97. 43%); 云冷杉在9 月下半月达落叶高峰期，10 月上半月凋落量次之，其他时期叶凋落量相差不大(变幅为3. 5% ～ 20. 20%)，相对于其他落叶树种，云冷杉在10 月后仍存在较大的凋落量。兴安落叶松在9 月下半月达落叶高峰，较高凋落量持续到10 月上半月，其他时期的总凋落量仅占总体的15. 82%。其他树种的总凋落量产生的LAI 较小，仅占所有树种的12. 53%，9 月上半月出现落叶高峰，9 月末叶凋落基本结束(凋落量达99. 01%)。云冷杉10 中旬之前叶凋落产生LAI 占同期所有树种的比例相差不大且较小(11. 78% ～ 27. 92%)，在10 月下半月明显高于其余树种(占总 LAI 的65. 46%); 兴安落叶松7 月份叶凋落产生 LAI 最小(占总LAI 的11. 13%)，其余树种相差不大; 在9 月下半月至10 月上半月叶凋落产生的LAI均占最大比例，分别为53. 02%，68. 72%(图 2)。白桦8 月份的叶凋落产生的LAI 最大，占该时期总LAI 的62. 43%。其他树种7 月及9 月上半月均占最大比例，但9 月下半月以后凋落量明显下降，在 10 月之后凋落基本结束，表明10 月后大部分树种凋落结束。

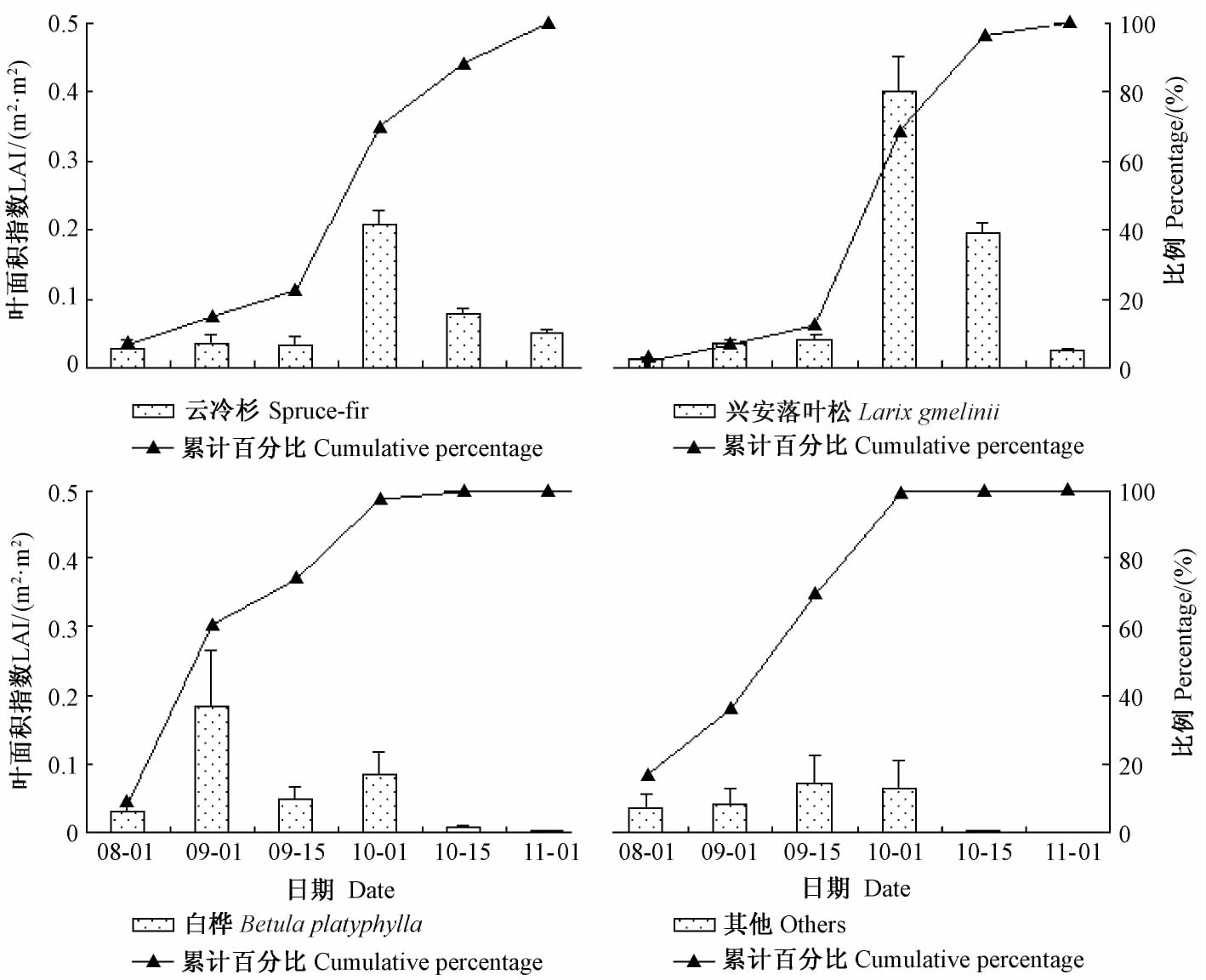
图1 各调查时期主要树种叶凋落产生的LAI Fig.1 LAI estimated from litter of major species during the investigation period

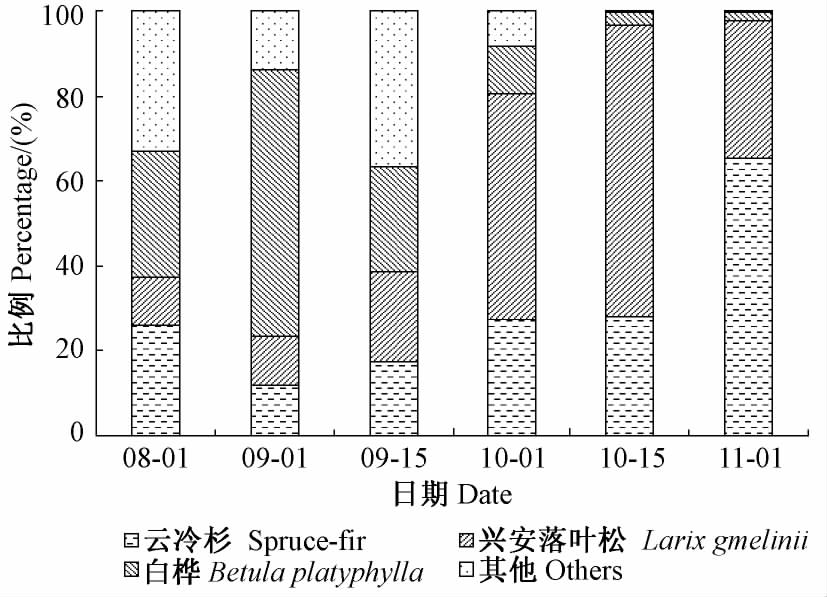
图2 各调查时期主要树种凋落叶产生的 LAI 占所有凋落叶产生总LAI 的比例 Fig.2 LAI estimated from litter of major species accounted for the proportion of the total LAI from all litter during the investigation period
2.3 有效叶面积指数与真实叶面积指数的季节性

LAIe不存在明显的季节性变化(表 4)，LAIe在 8 月初达到最大值为2. 44，仅比11 月份的最小值高20. 90%，不能灵敏地反映LAI 的季节性变化;相对而言，LAIt随时间推移明显减小，8 月份达到最大值3. 97，是11 月份最小值的1. 5 倍，体现了 LAI 的季节变化特性; 相对于LAIt，LAIe在整个调查期均出现低估现象，低估范围为28. 81 ～ 43. 24%，平均低估32. 98%。

表4 有效叶面积指数与真实叶面积指数的季节性① Tab.4 Seasonality of LAIe and LAIt
2.4 真实叶面积指数的空间格局

谷地云冷杉林落叶季节相同研究区内的LAIt，在最大时期(7 月)与最小时期(11 月)具有不同的空间异质性(表 5)。7 月LAIt由空间自相关引起的空间异质性占总空间异质性的99. 8%，主要表现在 4. 0 ～ 10. 44 m 的尺度上; 而由随机因素引起的空间异质性仅占总空间异质性的0. 2%，表现在4. 0 m以内的尺度上; 高密度斑块与低密度斑块均较少(图 3)。11 月LAIt由空间自相关引起的空间异质性的程度低于7 月，占总空间异质性的66. 9%，且仅在10. 98 m 的有效变程内LAIt存在明显的空间格局，高密度斑块面积较小，而中等密度斑块面积最大且分布集中，主要分布在样地边缘地带。7 月LAIt的基台值远大于11 月，说明7 月LAIt的空间异质性程度大于11 月。

表5 谷地云冷杉林7 月与11 月真实叶面积指数的空间格局变异函数参数 Tab.5 Parameters of semivariogram models of spatial pattern to LAIt for July and November in spruce-fir forest at valley

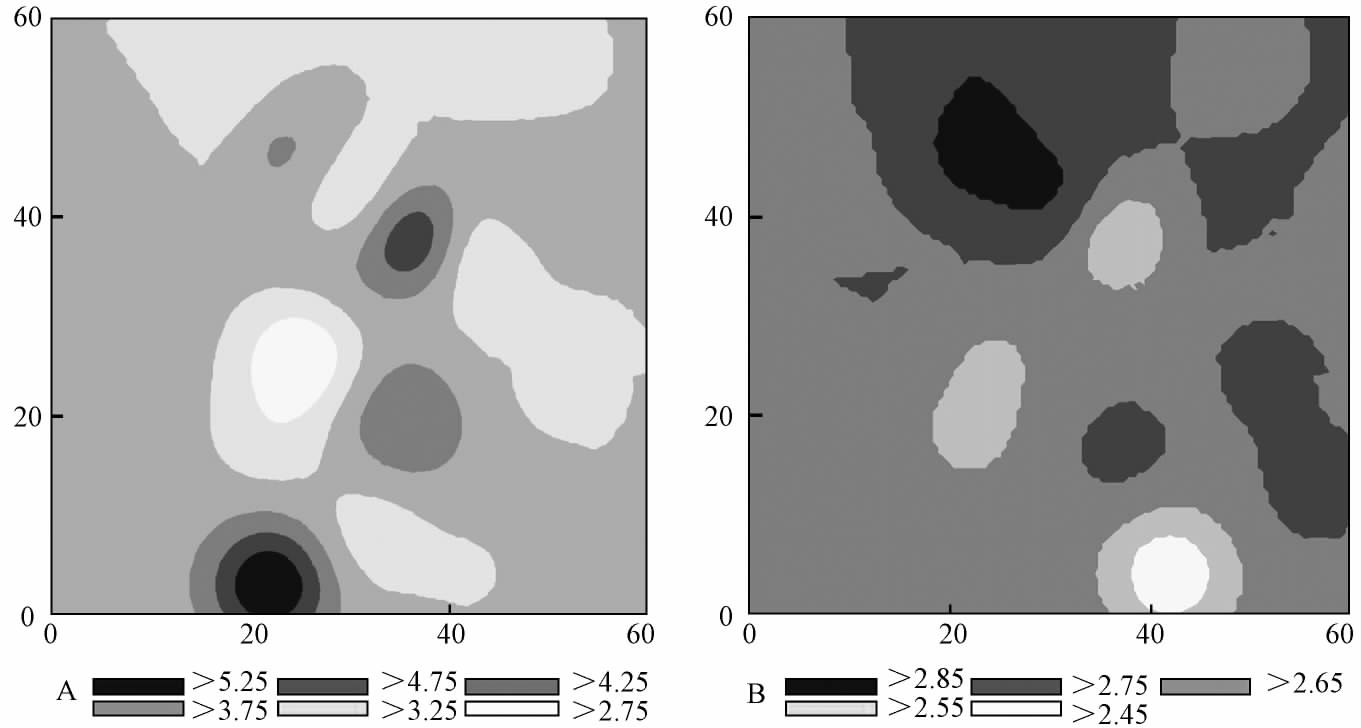
图3 谷地云冷杉林7 月与11 月真实叶面积指数空间格局 Fig.3 The spatial patterns of LAIt in July and November in Spruce-fir forest at valley A: 7 月July; B: 11 月November
3 讨论

凋落物法可准确、有效获得落叶林的LAIt(Neumann et al., 1989; Cutini et al., 1998; Bréda，2003)，合理校正光学仪器法获得的LAIe可得到较准确的常绿针叶林的LAIt(Chen，1996; Thimonier et al., 2010)，但单独利用这2 种方法均很难准确估测混交林LAI。小兴安岭谷地云冷杉林中落叶树种的相对优势度为32. 8%，本文尝试结合光学仪器法和凋落物法，对11 月初落叶树种完全落叶只剩常绿针叶时的LAIe进行木质部分、集聚效应的校正，校正后的LAI 结合凋落物法，得到小兴安岭谷地云冷杉林LAIt的季节动态。

木质部分和集聚效应是影响光学仪器法估测 LAI 测量精度的主要因素，光学仪器法计算LAI 过程中，因把木质部分当做叶子会增大LAI，而忽略集聚效应会减小LAI，针对以上情况，本研究分别进行校正。对于落叶林型，可利用光学仪器在展叶前或是落叶后测定木质部分的面积指数(woody areaindex，WAI)作为背景值，假设其他时期木质部分的影响不变，减去背景值来消除木质部分产生的影响，但此方法不适用于去除常绿林木质部分产生的误差。而本研究运用Photoshop 软件参照Qi 等(2012)的方法得到α 值为4% ～ 22%，其他学者得到类似结果，如Gower 等(1999)研究得到α 值 5% ～ 35%; Chen 等(2006)研究得到香脂冷杉(Abies balsamea)林的α 值为15% ～ 20%; Deblonde等(1994)估测挪威松林(Picea resinosa)及短叶松林(P. banksiana)的α 值分别为8% ～ 12%和10% ～ 33%。本研究中冠层水平的集聚指数ΩE由广泛应用的DHP-TRACWin 软件(Leblanc et al., 2005; Chen et al., 2006)直接获得，均值为0. 90，Chen 等(2006)利用相同方法得到香脂冷杉(A. balsamea)林的ΩE均值0. 95，主要树种为黑云杉(P. mariana)的林分，ΩE均值0. 91，均略高于本文研究结果，主要源于林分组成差异。

目前，国内关于常绿针叶树种簇内集聚效应的校正系数γE的研究较少报道，本研究通过实地采样量化了北方常绿针叶树种云杉、冷杉及红松的γE值，并根据各树种的胸高断面积比例加权得到谷地云冷杉林11 月初整个林分的γE为1. 2，其他学者得到类似结论，如Chen 等(2007)报道北方针叶林的γE为1. 4 ～ 1. 8，; Bréda等（2003）报道针叶林分的 γE为1. 2 ～ 2. 0。 相对于LAIt，光学仪器法估测的LAIe在LAI 最大时期低估43. 24%，主要源于此时属于叶茂盛期，冠层中的集聚效应远远大于木质部分的影响; 而在LAI 最小时期低估28. 81%，源于此时林分内只存在常绿树种，冠层中的集聚效应减弱，木质部分的影响此时最大。本研究利用半球摄影技术得到谷地云冷杉林8 月的LAIe为2. 44，探讨方法得到的LAIt为3. 84，其他学者也得到类似结果，如Thimonier等(2010)利用半球摄影技术测定云冷杉林2004 年 8 月初及2005 年7 月末的LAIe，分别为2. 3和2. 1; 将2005 年的LAIe进行曝光、集聚效应及坡度的校正后的值为3. 8。谷地云冷杉林虽为常绿针叶林，但也存在明显季节变化，7 月达最大值(3. 97)，8 月小幅度减小，9 月下半月减幅最大，11 月达最小值(2. 71)，总体变化幅度为31. 74%(表 4)，略大于Chen 等(2006)的针叶林LAI 季节变化幅度25% ～ 30%，主要源于树种组成、生境特性及阔叶树种在常绿针叶林中所占比例不同。

变异函数分析在生态学中的应用被证明是描述空间数据的有效方法(Fortin et al., 1989; Robertson，1987)。本研究用变异函数分析得到谷地云冷杉林 7 月LAIt的空间异质性程度大于11 月，主要源于7月大部分树种叶子达到成熟期，各样点的LAIt差异较大，而11 月落叶树种均凋落完毕，只剩常绿树种，各样点的差异相对减小，因此LAIt的空间异质性程度较小。

参考文献(References)
[1] 黑龙江 森林编辑委员会. 1993. 黑龙江森林. 哈尔滨: 东北林业大学出版社.(1)
[2] 李文华. 1980. 小兴安岭谷地云冷杉群落结构和演替的研究. 自然资源, (4): 17-29.(1)
[3] 李文华, 罗天祥. 1997. 中国云冷杉林生物生产力格局及其数学模型. 生态学报, 17(5): 511-518.(1)
[4] 吕瑜良, 刘世荣, 孙鹏森, 等. 2007. 川西亚高山暗针叶林叶面积指数的季节动态与空间变异特征. 林业科学, 43(8): 1-7.(1)
[5] Asner G P, Scurlock J M O, A Hicke J. 2003. Global synthesis of leaf area index observations: implications for ecological and remote sensing studies. Global Ecology and Biogeography, 12(3): 191-205.(1)
[6] Barr A G, Black T A, Hogg E H, et al. 2004. Inter-annual variability in the leaf area index of a boreal aspen-hazelnut forest in relation to net ecosystem production. Agricultural and Forest Meteorology, 126(3/4): 237-255.(1)
[7] Behera S K, Srivastava P, Pathre U V, et al. 2010. An indirect method of estimating leaf area index in Jatropha curcas L. using LAI-2000 Plant Canopy Analyzer. Agricultural and Forest Meteorology, 150(2): 307-311.(1)
[8] Bréda N J J. 2003. Ground-based measurements of leaf area index: a review of methods, instruments and current controversies. Journal of Experimental Botany, 54(392): 2403-2417.(3)
[9] Chen J M, Black T A. 1992. Defining leaf area index for non-flat leaves. Plant, Cell and Environment, 15(4): 421-429.(1)
[10] Chen J M. 1996. Optically-based methods for measuring seasonal variation of leaf area index in boreal conifer stands. Agricultural and Forest Meteorology, 80(2/4): 135-163.(1)
[11] Chen J M, Govind A, Sonnentag O, et al. 2006. Leaf area index measurements at Fluxnet-Canada forest sites. Agricultural and Forest Meteorology, 140(1/4): 257-268.(1)
[12] Chen J M, Rich P M, Gower S T, et al. 1997. Leaf area index of boreal forests: theory, techniques, and measurements. Journal of Geophysical Research, 102(D24): 29429-29443.(5)
[13] Coops N, Smith M, Jacobsen K, et al. 2004. Estimation of plant and leaf area index using three techniques in a mature native eucalypt canopy. Austral Ecology, 29(3): 332-341.(1)
[14] Cutini A, Matteucci G, Mugnozza G. 1998. Estimation of leaf area index with the Li-Cor LAI 2000 in deciduous forests. Forest Ecology and Management, 105(1/3): 55-65.(1)
[15] Deblonde G, Penner M, Royer A. 1994. Measuring leaf area index with the LI-COR LAI-2000 in pine stands. Ecology, 75(5): 1507-1511.(2)
[16] Fortin M J, Drapeau P, Legendre P. 1989. Spatial autocorrelation and sampling design in plant ecoloty. Vegetatio, 83(1/2): 209-222.(1)
[17] Gower S T, Kucharik C J, Norman J M. 1999. Direct and indirect estimation of leaf area index, f (APAR), and net primary production of terrestrial ecosystems. Remote Sensing of Environment, 70(1): 29-51.(1)
[18] Gower S T, Norman J M. 1991. Rapid estimation of leaf area index in conifer and broad-leaf plantations. Ecology, 72(5): 1896-1900.(1)
[19] Jonckheere I, Fleck S, Nackaerts K, et al. 2004. Review of methods for in situ leaf area index determination: Part I. Theories, sensors and hemispherical photography. Agricultural and Forest Meteorology, 121(1/2): 19-35.(1)
[20] Leblanc S G, Chen J M. 2001. A practical scheme for correcting multiple scattering effects on optical LAI measurements. Agricultural and Forest Meteorology, 110(2): 125-139.(1)
[21] Leblanc S G, Chen J M, Fernandes R, et al. 2005. Methodology comparison for canopy structure parameters extraction from digital hemispherical photography in boreal forests. Agricultural and Forest Meteorology, 129(3/4): 187-207.(2)
[22] Liu Z L, Jin G Z, Qi Y J. 2012. Estimate of leaf area index in an old-growth mixed broadleaved-Korean pine forest in northeastern China. PLoS One, 7(3): e32155. doi: 10.1371/journal.pone.0032155.(2)
[23] Luo T X, Li W H, Zhao S D. 1997. Distribution patterns of leaf area index for major coniferous forest types in China. Journal of Chinese Geography, 7(3): 61-73.(1)
[24] Macfarlane C, Grigg A, Evangelista C. 2007. Estimating forest leaf area using cover and fullframe fisheye photography: thinking inside the circle. Agricultural and Forest Meteorology, 146(1/2): 1-12.(2)
[25] Marshall J D, Waring R H. 1986. Comparison of methods of estimating leaf-area index in old-growth Douglas-fir. Ecology, 67(4): 975-979.(1)
[26] Muraoka H, Saigusa N, Nasahara K N, et al. 2010. Effects of seasonal and interannual variations in leaf photosynthesis and canopy leaf area index on gross primary production of a cool-temperate deciduous broadleaf forest in Takayama Japan. Journal of plant research, 123(4): 563-576.(1)
[27] Neumann H H, Den Hartog G, Shaw R H. 1989. Leaf area measurements based on hemispheric photographs and leaf-litter collection in a deciduous forest during autumn leaf-fall. Agricultural and Forest Meteorology, 45(3/4): 325-345.(1)
[28] Pinto-Júnior O, Sanches L, de Almeida Lobo F, et al. 2011. Leaf area index of a tropical semi-deciduous forest of the southern Amazon Basin. International Journal of Biometeorology, 55(2): 109-118.(1)
[29] Pueschel P, Buddenbaum H, Hill J. 2012. An efficient approach to standardizing the processing of hemispherical images for the estimation of forest structural attributes. Agricultural and Forest Meteorology, 160: 1-13.(2)
[30] Qi Y J, Jin G Z, Liu Z L. 2012. Optical and litter collection methods for measuring leaf area index in an old-growth temperate forest in northeastern China. Journal of Forest Research, DOI: 10.1007/s10310-012-0370-1.(2)
[31] Robertson G P. 1987. Geostatistics in ecology: interpolating with known variance. Ecology, 68(2): 744-748.(1)
[32] Sonnentag O, Chen J M, Roberts D A, et al. 2007. Mapping tree and shrub leaf area indices in an ombrotrophic peatland through multiple endmember spectral unmixing. Remote Sensing of Environment, 109(3): 342-360.(1)
[33] Sprintsin M, Karnieli A, Berliner P, et al. 2007. The effect of spatial resolution on the accuracy of leaf area index estimation for a forest planted in the desert transition zone. Remote Sensing of Environment, 109(4): 416-428.(1)
[34] Thimonier A, Sedivy I, Schleppi P. 2010. Estimating leaf area index in different types of mature forest stands in Switzerland: a comparison of methods. European Journal of Forest Research, 129(4): 543-562.(3)
[35] Wasseige C, Bastin D, Defourny P. 2003. Seasonal variation of tropical forest LAI based on field measurements in Central African Republic. Agricultural and Forest Meteorology, 119(3-4): 181-194.(1)
[36] Weiss M, Baret F, Smith G, et al. 2004. Review of methods for in situ leaf area index (LAI) determination: Part II. Estimation of LAI, errors and sampling. Agricultural and Forest Meteorology, 121(1): 37-53.(1)