林业科学  2013, Vol. 49 Issue (6): 1-9   PDF    
DOI: 10.11707/j.1001-7488.20130601
0

文章信息

商志远, 王建, 赵兴云, 张茂恒, 崔明星, 陈振举
Shang Zhiyuan, Wang Jian, Zhao Xingyun, Zhang Maoheng, Cui Mingxing, Chen Zhenju
樟子松树轮δ13C对气候因子响应的方位差异
Orientation Difference of Tree Ring δ13C Response to Climatic Factors for Pinus sylvestris var. mongolica
林业科学, 2013, 49(6): 1-9
Scientia Silvae Sinicae, 2013, 49(6): 1-9.
DOI: 10.11707/j.1001-7488.20130601

文章历史

收稿日期：2012-05-02
修回日期：2013-05-07

作者相关文章

商志远
王建
赵兴云
张茂恒
崔明星
陈振举

引用本文
商志远, 王建, 赵兴云, 张茂恒, 崔明星, 陈振举. 2013. 樟子松树轮δ13C对气候因子响应的方位差异[J]. 林业科学, 49(6): 1-9.
Shang Zhiyuan, Wang Jian, Zhao Xingyun, Zhang Maoheng, Cui Mingxing, Chen Zhenju. 2013. Orientation Difference of Tree Ring δ13C Response to Climatic Factors for Pinus sylvestris var. mongolica. Scientia Silvae Sinicae, 49(6): 1-9.  DOI: 10.11707/j.1001-7488.20130601
樟子松树轮δ13C对气候因子响应的方位差异
商志远1, 王建1, 赵兴云2, 3, 张茂恒1, 崔明星4, 陈振举5, 6    
1. 南京师范大学地理科学学院 南京 210023；
2. 山东省水土保持与环境保育重点实验室 临沂 276000；
3. 临沂大学资源环境学院 临沂 276000；
4. 中国科学院东北地理与农业生态研究所 长春 130102；
5. 沈阳农业大学林学院 沈阳 110866；
6. 中国科学院沈阳应用生态研究所 沈阳 110164
收稿日期：2012-05-02；修回日期：2013-05-07
基金项目：国家自然科学基金项目(41271204，41072139，40972112)；江苏高校优势学科建设工程项目(PAPD)。
摘要：对大兴安岭北部3株樟子松树轮进行δ13C测定，分析树轮δ13C对气候因子响应的方位差异以及不同采样方位数和方位组合方式对整轮代表性的差异。结果表明：樟子松树轮不同方位δ13C的均值序列对大区域气候环境因子的响应是一致的；树轮不同方位的δ13C序列多数呈正相关，少量呈负相关，其中相关系数达到显著性水平的序列多数呈对称分布；树轮不同方位δ13C序列提取气候因子的能力和程度存在较大差异；当无法整轮周向取样时，选取3~4个方位采样既经济高效又能较完整地提取样本的δ13C变化信息；在方位组合上，应尽量避免各孔向间呈180°夹角。
关键词： 树轮    δ13C    方位差异    气候要素    响应    樟子松    
Orientation Difference of Tree Ring δ13C Response to Climatic Factors for Pinus sylvestris var. mongolica
Shang Zhiyuan1, Wang Jian1, Zhao Xingyun2, 3, Zhang Maoheng1, Cui Mingxing4, Chen Zhenju5, 6     
1. College of Geographical Science, Nanjing Normal University Nanjing 210023;
2. Shandong Provincial Key Laboratory of Water and Soil Conservation and Environmental Protections Linyi 276000;
3. College of Resources and Environment, Linyi University Linyi 276000;
4. China Northeast Institute of Geography and Agroecology, Chinese Academy of Sciences Changchun 130102;
5. Forestry College, Shenyang Agricultural University Shenyang 110866;
6. Institute of Applied Ecology, Chinese Academy of Sciences Shenyang 110164
Abstract: Through investigation of the stable carbon isotope ratio (δ13C) of discs which were sampled from three 15-year-old trees in the north part of Daxing'anling Mountain, we analyzed the orientation variation in tree ring δ13C in response to climate factors and influence of sampling orientations and the sample combinations on the circumferential representative. The result showed that the impact of regional climate and environment factors on the variation in tree ring δ13C was consistent. It was found that most of the correlations between the tree ring δ13C sequences were positive, but some were negative. The sequences with significant correlation usually exhibited symmetrical or obtuse-angled distribution. The capability and extent of tree ring δ13C extracting the climate factors varied obviously among different orientations which accounted for the responses of different orientations to climate factors. The result suggests that 3 orientations provide the best and most efficient choice for extracting the information of tree ring δ13C. Sampling should avoid boring in one direction only, but should also include transversal angles.
Key words: tree rings    δ13C    orientation difference    climatic factors    response    Pinus sylvestris var. mongolica    

树轮稳定碳同位素在研究气候或环境重建中发挥着独特而重要的作用(冀春雷等，2010 ; Liñán et al.，2011)。许多研究发现，年轮不同方向上的稳定碳同位素比率(δ13 C 值)存在显著差异(Ramesh et al.，1985 ; Nguyen-Queyrens et al.，1998 ; 赵兴云等，2012)。树轮稳定碳同位素的气候意义研究目前还处于初级阶段(陈宝君等，2002 a; 2002 b; 王建等，2006)。Francey(1981)认为用某个方位的δ13 C 值可以代表整个年轮的δ13 C 值，Mazany等(1980)和Leavitt等(1984)认为用多个方位的δ13 C 均值代表整个年轮值更合理。陈宝君等(2002 b)认为采用多个方位平均或整轮取样的方法会相对降低气候重建研究的精度和可靠性。王建等(2008)认为选择2~4个方位并尽量使各方位之间成钝角既经济方便又能充分反映树木整体δ13 C 变化信息。目前，有关树轮δ13 C 对气候要素响应方位差异的研究仍处于探索之中。本研究分析大兴安岭北部樟子松(Pinus sylvestris var． mongolica)树轮δ13 C 对气候因子响应的方位差异，并探讨不同采样方位数和组合方式对整轮δ13 C 序列的代表性，以期为今后经济高效地进行树芯样本采集提供依据。

1 研究区概况

研究区地处大兴安岭伊勒呼里山北坡，采样点位于新林林业局下辖碧洲林场境内(124 ° 13 '—124 °36 ' E，51 ° 57 '—52 ° 00 ' N)，自然区划上归属大兴安岭针叶林区的北部亚区，北临黑龙江支流呼玛河上游，南界为伊勒呼里山山脊，平均海拔670 m。寒温带大陆性季风气候，年均气温-2.54 ℃，年降水量519.4 mm，降水集中在6月下旬至9月中旬，年均日照时数2 383.6 h，全年无霜期90~100天。年总辐射量4 200 MJ·m -2，年蒸发量952.7 mm，≥10 ℃年积温1 430 ℃。研究区地带性植被为寒温带明亮夏绿针叶林。优势种为兴安落叶松(Larix gmelinii)、樟子松和白桦(Betula platyphylla)，此外，河谷及冲积地有云杉(Picea koraiensis)、甜杨(Populus suaveolens)和钻天柳(Chosenia arbutifolia)等树种分布(詹昭宁等，1995 ; 张万里等，2000)。

2 材料与方法

2005年1月，在林场下辖大青山十支线地区采集3株原始林樟子松盘片(编号分别为 A，B和C)用于分析树轮δ13 C 方位变化特征，样品生长受人类活动影响较小。另外用生长锥在林场后山采集31株天然次生林樟子松的71根生长锥样芯用于交叉定年。样品采集过程与定年均按国际树轮数据库标准完成。样品具体信息见表 1 。

表 1 樟子松树轮样品信息 Tab.1 Basic information of the tree ring δ13 C samples

样品采集时做好方位标识，运回实验室后晾干，用干砂纸打磨样本表面至年轮界线清晰可见。利用AcuRite 年轮宽度仪的 MeasureJ2 X 量测系统对样本的逐年生长轮分别按东南西北4个方位进行宽度测量，测量精度0.001 mm，并利用 COFECHA 程序对宽度序列进行交叉定年检验，经交叉定年判定3样本最外一轮均为2004年。以髓心为中心，以45 °间隔顺时针将样盘表面依次划分为北、东北、东、东南、南、西南、西和西北共8个方位，并依次做好标记。经综合比较，确定3样本剥取时段均为1990 —2004年的连续15年，均按上述8个方向用手术刀逐年进行剥取。剥取的样本在电子天平上称质量，剥离称量过程严格防止样品相互之间的混淆及外来杂质的混入。采用索式抽提法对本研究样品进行纤维素提取，并抽样选取提取好的纤维素样品，通过傅里叶变换红外光谱仪(FTIR NEXUS670型)进行红外光谱扫描分析，结果表明此流程提取的综纤维素样品纯度符合标准，满足研究要求。利用同位素比例质谱仪(ThermoFinnigan-DeltaplusXP)测定综纤维素样品的碳同位素13 C / 12 C 之比，采用尿素标准样(UREA，δ13 C =-49.1 ‰)进行校验，测定结果相对于 PDB 标准表示为δ13 CPDB(简写为δ13 C，分析误差≤0.15 ‰)。结果以 Excel 2003格式输出，采用SPSS17.0进行数据分析，采用 Origin8.0绘图。

3 结果与分析 3.1 树轮δ13 C 的方位变化特征

3样本8个方位的15年δ13 C 序列见图 1 。由图 1可见，3样本各方位δ13 C 序列的变化趋势大体一致。样本 A 与 B、A 与 C和B 与 C 之间8个方位均值序列的相关系数分别为0.324，0.555和0.690，A 与 C和B 与 C 之间分别在0.05和0.01水平显著相关，反映出3样本δ13 C 值年际变异对区域气候环境要素的响应大体一致，这一点与前人在其他地区的研究结果(赵兴云等，2006)类似。此外，3样本同一年不同方位的δ13 C 平均极值之差分别达到2.212 ‰(样本 A)，2.429 ‰(样本 B)和2.393 ‰(样本 C)，说明不同方位之间的δ13 C 存在着不可忽视的差异。

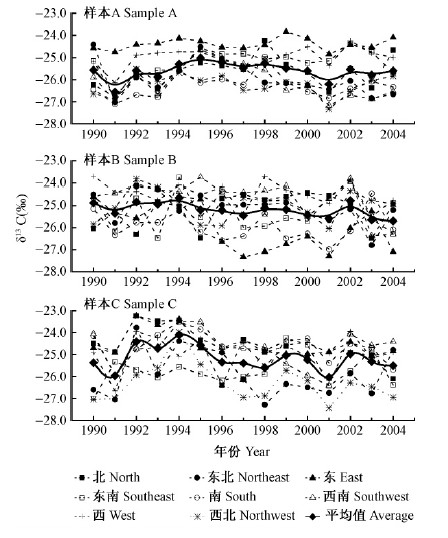图 1 3样本8个方位的 δ13 C 年序列 Fig. 1 The δ13 C sequences of eight radii andaverage sequencesfor each samples

3样本各方位之间的δ13 C 值相关系数见表 2，由表 2可见，每个样本的8个序列之间大多呈正相关，但也有少量呈负相关，此点与前人的研究(Stuiver et al.，1984 ; Sheu et al.，1995 ;Schleser et al.，1999 ; 陈宝君等，2002 b)有所不同。

表 2 树盘样本不同方位δ13 C 序列相关系数 ① Tab.2 Correlation coefficients between different δ13 C sequences for different radii

由表 2可见，3样本各方位δ13 C 序列之间的相关性各有不同:样本 A 普遍正相关，相关系数为0.019~0.818 ; 样本 B 约2 /3的序列之间呈正相关，约1 /3呈负相关，相关系数为-0.677~0.695 ;样本 C 约6 /7的序列之间呈正相关，约1 /7呈负相关，相关系数为-0.321~0.901 。进一步分析可见，3样本呈正相关的序列之间多数呈对称方向或钝角方向，且其中相关系数达到显著性水平的比例接近1 /4 。

3.2 树轮δ13 C 序列与气候因子的相关分析

为尽可能排除树木不同生长阶段特性对气候重建的影响，所选取的δ13 C 测定阶段应尽可能处于树木生长的稳定期或衰老期。由3样本原始宽度的测量结果(图 2)可知3样本选取的δ13 C 测定时段(1990 —2004)已处于生长稳定期，高低频分离以进行去趋势的必要性已不大，利用δ13 C 原始序列与气候要素指标进行相关分析能够满足要求(陈宝君，2002 a)。

图 2 3样本原始宽度序列(均为东西南北4个方向平均值) Fig. 2 Tree ring width of three samples (all are average of north,east,south,and west)

在利用树轮δ13 C 序列进行气候因子分析之前，为了能够较真实地反映树轮δ13 C 所记录的气候因子变化，通常需要预先剔除序列中主要受大气 CO2浓度变化等影响的低频部分，而保留主要受温度降水等气候因子影响的高频部分。但低频去除的过程中有可能同时去除了部分气候信息，且目前尚无统一标准。鉴于本研究分析所用资料时段仅15年，且处于生长稳定阶段，借鉴前人研究(陈宝君，2002 a)，本研究未作高低频分离。气象资料选用采样点附近的新林气象站自1972年建站以来的逐月降水和平均气温资料。对气象站1972 —2004年气象数据进行均一性分析和时间序列的突变检验，经滑动 t 检验和Mann-Kendall 时间序列趋势检验，气温和降水时间序列在该时段均未发生均值突变，满足气候重建要求。表 3中列出了3样本各自单方位δ13 C 序列及8个方位均值序列与新林站相关气象指标在0.05水平显著相关的代表性气候因子。

表 3 树轮各方位δ13 C 序列与气候因子的相关性 ① Tab.3 Correlation between the δ13 C sequences of various orientations and the climatic factors

由表 3可见，3样本从各自单一方位序列中均能够提取出若干个气候因子，而从8个方位均值序列中只能提取出3~4个气候因子，基本体现不出平均值的优势，甚至会削弱对气候要素的响应能力，这一点与前人的研究(陈宝君等，2002 b)相类似。

进一步分析可见，对于不同方位，有的方位可以提取多达5~6个重要的气候因子(如样本 A和B的东向，样本 C 的东北、东南和西南向)，而有的方位未能提取出达到显著性水平的气候因子(如样本B 的东南向和西北向，样本 C 的正北和正南向)，提取因子的多少和相关性的强弱相互差异很大。从表 3还可以看出树轮不同方位的δ13 C 序列之间存在共线性问题，为尽量避免方位之间的相互影响，同时研究δ13 C 随时间和方位的变化特征，对δ13 C 序列的矩阵进行主成分分析。先将8个方位的δ13 C 序列转换成相互正交的8个主成分，再以这些主成分作为预报因子来重建相应的气候要素。分析结果显示3个样本的 KMO(Kaiser-Meyer-Olkin)值在0.5左右，表明各序列之间的偏相关性较差，即相关程度有较大差异，其中样本 A和B 的球形假设被拒绝，表明8条序列之间存在一定的相关性。

各主成分对应的特征值、荷载矩阵和方差贡献率见表 4 。由表 4可见，3样本均需要至少前4个主成分才可使得方差总贡献率达到65 % 以上，说明并非前1个主成分即可代表各方位Δδ的最主要的共同变化特征，而有可能需要前4~5个主成分才能满足要求，可视作8个方位的加权平均。

表 4 3样本δ13 C 序列主成分 Tab.4 Principal component for the δ13 C sequences of samples

对3个样本的各自8个主成分分别与新林气象站逐月、生长季及全年的气象指标做相关分析，将部分与主成分在0.05水平显著相关的代表性气候因子列于表 5 。由表 5可知，3样本不同主成分与气象指标的相关性各有差异。

表 5 与主成分相关的代表性气候因子 ① Tab.5 The representative climatic factors correlating with principal components(PCs)
3.3 树轮δ13 C 采样方位的组合分析

本研究未进行全轮周向均匀剥取样品来测定整轮样品δ13 C 值，采用8个方位的平均值近似代表整轮样品的δ13 C 均值。参考相关文献(王建等，2008)，分别计算每个样本单一方位的δ13 C 序列与整体8个方位均值序列之间的相关系数，取均值作为方位数为1时的相关系数平均值; 同理计算2个方位组合的均值序列与整体8个方位均值序列之间的相关系数，取均值作为方位数为2时的相关系数平均值; 依此类推，从而得到方位数分别为1~7的相关系数平均值。同理，再继续比较单一序列均值以及不同方位组合序列均值与整体8个方位均值序列之差的平方和与样本数的商、各序列与整体8个方位均值序列逐年差值平方和的均值与样本数的商、序列平均标准差与8个方位平均序列标准差的差等指标，以分析他们与整轮序列的相关程度和相似性，并分别做图(图 3)。

图 3 4个指标(相关系数平均值、不同方位组合序列均值与整体8个方位均值序列之差的平方和与样本数的商、各序列与整体8个方位均值序列逐年差值平方和的均值与样本数的商、序列平均标准差与8个方位平均序列标准差的差)随取样方位数的变化 Fig. 3 Variation of four indices(the average of correlation coefiicient between the different combination sequence and the average sequence of 8 radii,the ratio of the sum of square of the difference between the average of combination sequences and the average of 8 radii to the number of sample,the ratio of the average of the sum of squares of annual difference between the average of combination sequences for different radii and the average of 8 radii to the number of sample,and the differences between the average standard deviation of combination sequencesand the standard deviation of the average of 8 radii)with the number of sampling radii

从相关系数平均值(图 3)来看，不同方位组合的均值序列与8个方位均值序列的相关系数随方位数的增多而增大，但其增大的速度呈指数递减，说明随着组合方位数的增多，方位组合对整轮序列的代表性由显著逐渐变为不显著。当方位数达到3个时，相关系数的平均值最低即已达到0.7以上。单一序列均值以及不同方位组合序列均值与整体8个方位均值序列之差的平方和与样本数的商反映了序列均值与整轮序列均值之间的相近程度，由图 3可见该值随方位数增多而减小，但减小速度呈指数下降，即平方和均值的减少对于代表性改善的效果也是由显著逐渐变为不显著，当方位数达到3个时，即已降至0.1以下。各序列与整体8个方位均值序列逐年差值平方和的均值与样本数的商反映了各序列与整轮序列之间的差异大小。差值平方和越小，表明序列与整轮序列的差异越小。同样可见，该值随方位数增加而减小，但增加速度亦呈指数递减，当方位数达到4个时，差值平方和已趋于稳定。标准差反映了序列变化的性质，标准差越相近，说明2个序列的波动幅度和频率越相似。从序列平均标准差与8个方位平均序列标准差的差来看，该值随着方位数增加迅速减少，但仍呈指数下降趋势，在方位数达到4个时，3样本序列标准差与整轮序列标准差的差值均已降至0.1以下。综上所述，3~4个方位合并分析已经完全能够满足要求，既经济方便又较充分地反映样本δ13 C 的变化信息，这一点与前人研究的结论基本一致(王建等，2008)。

在3样本各自8个方位中，取2~6个不同方位组合的均值序列与8方位均值序列进行相关分析，相关系数见表 6 。由表 6可以看出，当选取2个方位采样时，采样孔向呈直角的相关性最好，呈对称方向的相关性最差; 3个方位采样时，孔向分布呈45 °-90 °-225 °最好，45 °-135 °-180 °最差; 而4~6个方位采样时，采样孔向均为 n-1个锐角加1个钝角(n 为采样方位数)的方式最好，基本也是孔向对称或大致对称分布的方式最差。总体而言，随着采样方位数的增加，同一采样方位数内，不同夹角布局的采样方式的相关系数差别逐渐减弱。

表 6 不同组合方式下的样本组合均值序列与整轮序列的相关系数 Tab.6 The correlation coefficients between the combined average sequence indifferent combination mode and average sequence of eight radii
4 结论与讨论

本研究表明，樟子松树轮多年δ13 C 的均值序列对区域气候环境变化的响应是一致的。树轮同一年不同方位的δ13 C 存在显著差异。 Ramesh等(1985)认为气候因子的变化会影响树体细胞的活跃程度，从而产生生长激素的非对称分布或侧向再分配。

樟子松树轮不同方位的δ13 C 序列对气候因子响应的能力有所不同，不同方位δ13 C 序列提取气候因子的数量和相关性的强弱等方面存在较大差异。此外，由表 3还可以发现，对于同一气候因子，不同方位的相关性多数相同，但少数方位却呈现截然相反的趋势，这也暗示各方位取平均值的δ13 C 序列很可能会削弱对气候要素的响应能力，造成这一现象的原因有待探讨。此外，多数方位δ13 C 序列都与生长季早期的月最高气温负相关，而与生长季晚期的月最高气温正相关; 而月最低气温这一指标恰好相反，多数方位δ13 C 序列与生长季早期的月最低气温正相关，而与生长季晚期的月最低气温负相关。导致这一现象的原因也值得深入研究。

在确定采样方位的具体数量方面，当客观条件无法满足整轮周向取样时，选择3~4个方位采样既经济高效又能较完整地提取样本的δC 变化信息。在采样方位的具体组合方面，2个方位采样时，采样孔向呈直角的相关性最好，呈对称方向的相关性最差; 3个方位采样时，孔向分布呈45 °-90 °-225 °最好，45 °-135 °-180 °最差;而4~6个方位采样时，采样孔向均为 n-1个锐角加1个钝角(n 为采样方位数)的方式最好，基本也是孔向对称或大致对称分布的方式最差。结合表 2可见，3样本各自不同方位的δ13 C 序列之间多呈“对称相关”，即相关性达到显著性水平的序列多数呈对称分布或钝角分布。这说明对称或大致对称方向的方位组合，相对增加了序列之间的共性关系，也就在一定程度上削减了组合序列的整体代表性，从而显示较差的相关性。因此，应尽量避免对称方向取样。但随着采样方位数的增加，同一采样方位数内，不同夹角布局的采样方式的相关系数差别逐渐减弱，这也就意味着如采样方位数达到4个或以上时，孔向布局和组合工作的重要性已不大。值得说明的是，本研究结论是对我国寒温带季风气候区的樟子松样本分析所得到的，分析的序列时段相对较短(均仅15年)，其适用性和指导性有待于今后深入研究。

参考文献(References)
[1] 陈宝君,钱君龙,濮培民,等. 2002a.树轮α-纤维素δ13C角分布及其气候意义.南京林业大学学报:自然科学版, 26(1): 14-18.(3)
[2] 陈宝君,钱君龙,濮培民,等. 2002b.树轮δ13C的角分布及其在气候重建中的应用.南京气象学院学报,25(4): 463-471.(4)
[3] 冀春雷,徐庆,靳翔,等.2010.树木年轮碳氢氧稳定同位素在全球气候变化研究中的应用.林业科学, 46(7): 129-135.(1)
[4] 王建,钱君龙,梁中,等.2008.树轮稳定碳同位素分析的采样方法——以天目山柳杉为例.生态学报,28(12): 6070-6078.(3)
[5] 王建,赵兴云,钱君龙. 2006.天目山柳杉树轮δ13C方位变化及成因探讨.地理研究,25(2): 242-254.(1)
[6] 詹昭宁. 1995.中国森林立地类型:第1版.北京:中国林业出版社, 57-62.(1)
[7] 张万里,李雷鸿. 2000.大兴安岭新林林业局森林资源可持续发展的技术体系.东北林业大学学报,28(5): 130-133.(1)
[8] 赵兴云,王建,钱君龙,等.2006.天目山柳杉树轮δ13C年序列差异.应用生态学报, 17(3): 362-367.(1)
[9] 赵兴云,王建,商志远,等. 2012.树轮δ13C值方位分布及年际变化的普遍性研究——以中国东部亚热带地区为例.地理科学,32(2): 193-198.(1)
[10] Francey R J. 1981.Tasmanian tree rings belie suggested anthropogenic 13C/12C trends. Nature, 290(5803): 232-235.(1)
[11] Leavitt S W, Long A.1984. Sampling strategy for stable carbon isotope analysis of tree in pine. Nature,311(5982): 145-147.(1)
[12] Liñán I D, Gutiérrez E, Helle G,et al. 2011.Pooled versus separate measurements of tree-ring stable isotopes. Science of the Total Environment, 409: 2244-2251.(1)
[13] Mazany Y, Lermen J C, Long A. 1980. Carbon-13 in tree-ring cellulose as an indicator of past climates. Nature, 287(5781): 432-435.(1)
[14] Nguyen-Queyrens A, Ferhi A, Loustau D, et al. 1998. Within-ring δ13C spatial variability and interannual variations in wood cellulose of two contrasting provenances of Pinus pinaster. Canadian Journal Forest Research, 28: 766-773.(1)
[15] Ramesh R, Bhattacharya S K, Gopalan K. 1985. Dendroclimatological implications of isotope coherence in trees form Kashmir Valley, India. Nature, 317(6040): 802-804.(2)
[16] Schleser G H, Helle G, Lücke A, et al. 1999. Isotope signals as climate proxies: the role of transfer functions in the study of terrestrial archives. Quaternary Science Reviews, 18(7): 927-943.(1)
[17] Sheu D D, Chiu C H. 1995.Evaluation of cellulose extraction procedures for stable carbon isotope measurements in tree ring research. International Journal of Environmental Analytical Chemistry, 59(1): 59-67.(1)
[18] Stuiver M, Burk R L, Quay P D. 1984. 13C/12C ratios in tree rings and the transfer of biospheric carbon to the atmosphere. Geophysics Res, 89(D10): 11731-11748.(1)