Spatial patterns of tree locations in a forest standreflect the complex historical and environmental mosaicimposed by initial establishment patterns, microenvironment differences, climatic factors, competing vegetation, management activities, and thechance success of different species or individuals overtime.The spatial distributions of trees strongly affectcompetition between neighboring trees, size variabilityand distribution, growth and mortality, and crownstructure (Kuuluvainen et al., 1987; Kenkel, 1988; Miller et al., 1989; Hara, 1992; Moeur, 1993; Rouvinen et al., 1997; Dovciak et al., 2001). Furthermore, the spatial patterns at tree-scale havelarge influences on system-level and community-levelproperties of ecosystem functions (Pacala et al., 1995; Friedman et al., 2001). In general, positive spatialdependence among neighboring trees is mainly due tothe effects of the micro-site, whereas inter-treecompetition tends to create negative spatial dependenceamong neighboring trees (Fox et al., 2001).

Spatial point pattern analysis is commonly used tostudy the distributions of the horizontal spacing amongtrees within a region of interest.The objective ofspatial point pattern analysis is to measure howindividual trees are located with respect to each otherby using quantitative characteristics and to describe the“laws” regulating the locations with mathematicalmodels (Diggle, 1983; Tomppo, 1986; Pretzsch, 1997). There are three fundamental spatial pointpatterns: complete spatial randomness (CSR), regularity, and clustering.This classification is oversimplified, but useful at an early stage of spatialanalysis.It is also helpful to formulate a model for theunderlying spatial point process (Diggle, 1983). Aspatial point pattern is the realization of a spatial pointprocess (Cressie, 1993). Once the spatial pointpatterns are recognized, it is desirable to fit appropriatepoint process models to the spatial patterns in order tounderstand the mechanisms generating the patterns andto perform analyses of goodness-of-fit for the models.Detailed review on spatial point process models can befound in the literature (Cressie, 1993; Tomppo, 1986; Stoyan et al., 2000).

The spatial point process generating CSR is calleda homogeneous Poisson process, such that the numberof events realized by this process 1)follow a Poissondistribution with mean equal to λ A, where λ is thedensity or intensity of events (e.g., trees)and A isthe area of the region A; and 2)are independentrandom samples from the uniform distribution on A (Cressie, 1993; Diggle, 1983). Intuitively, CSRmeans that events are equally likely to occur anywherewithin A and that events do not interact with each other (Cressie, 1993). The homogeneous Poisson pointprocess usually serves as a null model (Stoyan et al., 2000). If the null model is rejected, more complicatedmodels are necessary to be tested (Tomppo, 1986).

One such model is the Gibbs point process model (or pairwise interaction process model), whichassumes the interaction between two events (e.g., trees) depends on the relative location of them.Itoriginates from statistical physics (Wood, 1968;Landau et al., 1980)and has been intensively used inspatial statistics (Stoyan et al., 1987; Ogata et al., 1981; 1984; 1985; Diggle et al., 1994). The Gibbspoint process model with pair potential functions is aclass of models for point patterns exhibiting interactionsbetween the events.These models have been appliedin forestry and ecological studies due to their greatflexibility and realism in modeling different spatialpoint patterns (Tomppo, 1986; Penttinen et al., 1992;Stoyan et al., 1998; Särkkä et al., 1998; Stoyan et al., 2000).

Different methods have been developed to estimatethe parameters of the pair potential functions.Diggle etal. (1994)summarizes three general methods, namelyapproximations of maximum likelihood, maximumpseudo-likelihood, and Takacs-Fiksel method.Thesemethods can be routinely used in applications and thereare no restrictions on the parametric form of the pairpotential functions (Tomppo, 1986; Stoyan et al., 1987; Jensen et al., 1991).

Spruce-fir stands in the Northeast, USA aretraditionally important resources for timber production.Forest managers and researchers have developed avariety of tools for managing these stands.These toolsinclude stocking charts and stand density managementdiagrams for the pure and mixed softwood stands in theregion (Solomon et al., 2002). However, very littlespatial information is available for these stands to date.The objectives of this research were 1)to explore thespatial structures of the spruce-fir softwood stands inthe Northeast, USA, 2)to fit the Gibbs point processmodel with three pair potential functions to the spatialpatterns of trees within the stands, and 3)to developempirical regression models for predicting theparameters of the Gibbs point process model usingavailable stand variables.

Fifty (50)plots were collected from the even-aged spruce-fir forests in northwestern Maine, USA, located in the region between 69 °W and 71 °W inlongitude, between 45 °N and 46.5 °N in latitude, andbetween 750 m and 1 200 m in elevation (Kleinschmidt et al., 1980). The plot size ranged from0.002 5 to 0.02 hm².The shapes of the plots weremostly square with a few rectangular.In each plot, theposition of each tree over 1.37 m in height was mapped (Li et al., 2007). In these plots balsam fir (Abiesbalsamea)and red spruce (Picea rubens)accountedfor about 95% of total number of trees and 94% oftotal volume. Other minor species included blackcherry (Prunus serotina), eastern white pine (Pinusstrobus), white spruce (Picea glauca), black spruce (Picea mariana), and other hardwoods.Tree diameterat breast height (DBH), total height, crown length (top to the base of crown), and average crown widthwere recorded for each tree (Solomon et al., 2002). The numbers of trees in each plot ranged from 12 to109.Mean tree diameters were from 2.2 to 19.2 cmand mean tree total heights were from 2.7 to 17.1m (Tab. 1).

Tab.1 Summary statistics of the stand variables across the 50 plots

Tab.1 Summary statistics of the stand variables across the 50 plots Stand variables Mean Std. Min. Max. Number of trees per plot 34.4 17.7 12 109 Stand density/ (tree•m-2) 0.61 0.54 0.18 2.52 Stand basal area/ (m2*hm2) 50.2 14.3 10.0 79.6 Stand mean DBH/cm 11.5 3.9 2.2 19.2 Stand mean height/m 11.6 3.7 2.7 17.1 Stand mean crown length/m 4.4 1.5 1.6 8.4 Stand mean crown width/m 1.1 0.3 0.5 1.9

Using the methods of refined nearest neighborstatistic, Ripley's K-function (Ripely, 1976)analysisand pair correlation function analysis, 24 plots wereclassified as completely spatial random (CSR)pointpattern, 17 plots as regular point pattern, and 9 plots asclustered point pattern out of the 50 plots (Li et al., 2007). The classification was used as the basis formodeling the spatial patterns in this study.

Suppose thespatial point pattern in a mapped forest plot A has Nevents (trees). Denote X={X_i= (u_i, v_i)∈A: i=1, 2, …, N} as the set of coordinates (u_i, v_i)of thetrees.The forest plot A is a sampling window within amuch larger forest region.Therefore, the events (trees)are the points of a partial realization of aplanar point process within A. For the patterns of Ntrees in a bounded region A, the pairwise interactionprocesses (i.e., pair-potential processes)are suitablestochastic models.The joint density for these processesgenerally takes the form of

where $\left\| \cdot \right\|$ is the Euclidean distance between trees iand j, β is a parameter determining the intensity of theprocess, Φ (·)is a pair potential function, and C is anormalizing constant to make f (x)a density dependingon β and Φ (·).

The homogeneous Gibbs point process is a specialcase of pairwise interaction processes.It ischaracterized by the potential function Φ (·)andanother parameter α=-log (β). Although the explicitform of the distribution is hard to obtain, the followingrelationship holds for a homogeneous Gibbs pointprocess (Diggle et al., 1994)

where λ is the density of events, E₀ is the expectationwith respect to the Palm distribution of the process, E is the expectation, and Z (X)is any random functionof the process where X includes all events of theprocess in the whole plane.For a strict definition ofPalm distribution, see Stoyan et al. (1987), Tomppo (1986)and Cressie (1993).

However, when it is conditional on the number ofpoints N, Gibbs distribution can be expressed as

where Z is the normalizing constant in the form of

$ Z = \int_{{A^N}} {\exp \left[ { - \sum\limits_{1 \leqslant i{\text{ < }}} {\sum\limits_{{\text{j}} \leqslant {\text{N}}} {\Phi \left ( {\left\| {{{\text{X}}_{\text{i}}}{\text{ - }}{{\text{X}}_{\text{j}}}} \right\|} \right)} } } \right]d{X_1}, \cdots } d{X_N} $

The pair potential function Φ (·)can be interpreted asfollowings: Φ (d)＞ 0 indicates that the probabilitydensity for inter-event distance d is lower than thatunder Poisson process and, thus, there is repulsion atdistance d; Φ (d)＜ 0 indicates that the probabilitydensity for inter-event distance d is higher than that under Poisson process.Thus, there is attraction atdistance d; and Φ (d)=0 indicates a Poisson process.

The pair potentialfunction Φ (·)can be parameterized in various forms.In this study, three parametric models were adopted.The first one is called Very-Soft-Core (VSC)pairpotential function (Ogata et al., 1984):

where δ is a scaling parameter.For the VSC pairpotential function, the range of interaction is infinitefor all distance r.The second one is called Diggle'spair potential function that has the following form (Diggle et al., 1994):

where the scaling parameter δ defines the range ofinteraction.The third one is called Ogata andTanemura's pair potential function (Ogata et al., 1985):

where the scaling parameter δ defines the range ofinteraction.Notice that equation (4)is a special case ofequation (6)when the parameter τ=0. For equation (5), Φ (r)$ \equiv $0 when r=δ representing the Poissonprocess.For equation (6), Φ (r)$ \equiv $0 when τ=δ/r, which represents the Poisson process.

One of themethods for estimating the parameters of the pairpotential functions is the Takacs-Fiksel method (Diggle et al., 1994). It is based on the fundamentalrelationship in equation (2). Suppose θ is theparameter vector of a pair potential function [θ=δ forthe potential functions (4)and (5)or θ= (τ, δ)for thepotential function (6)].If a series of test functions Z_k (k=1, 2, …, m)are chosen to estimate both sides ofequation (2) (denoting the left side as ${\hat L_k}\left ({\alpha, \theta } \right)$ andthe right side as ${\hat R_k}\left ({\alpha, \theta } \right)$, the sum of squareddifferences of both sides can be minimized to estimatethe model parameters (α, θ)as,

where m is some arbitrary number no less than thelength of parameter vector (α, θ).

There is no agreed rule for choosing the functionZk .However, if the test function Zk is chosen to beequal to Nj (rk) (Diggle et al., 1994), which is thenumber of events i with $\left\| {{X_i} - {X_j}} \right\| \leqslant {r_k}$, where X_j (j =1, 2, …, L)is the jth randomly chosen testing point, the left side of equation (2)can be estimated as

where K (r_k)is Ripley's K-function (Ripley, 1976; 1977). The right side of equation (2)can beestimated as

The choices of L, m and r_k are arbitrary althoughdifferent values can be tried and compared.For thedata used in this study, we set the constants asfollows: 1)L=2N because we wanted to ensure thatthere were enough random points surrounding a tree, and 2)m=30 and r_k=0.1k (which made themaximum value 3.0 m)because we wanted there to beenough but not too many trees within the plot which areconsidered interacting with each other.

The optimization of equation (7)was performedusing a direct search polytope algorithm (one availablesubroutine is the UMPOL in the IMSL Math Library ofFortran PowerStation 4.0 ℃ 1994-95 MicrosoftCorporation). Details of the polytope algorithm can befound in the literature (Nelder et al., 1965; Gill et al., 1981).

Typically, the studyregions would be the sampled plots within a foreststand.Each of these plots covers only a part of theentire spatial pattern.Interactions can only beobserved among the trees within a plot, whileinteractions are unobserved between the trees withinthe plot and the trees outside the plots.It is known asthe edge or boundary effect.If no correction is takenfor the boundary effect in the point pattern analysis, the estimation of the interactions is biased.In theprevious study (Li et al., 2007), the toroidal edgecorrection method was proven to be simple andsatisfactory compared with other available edgecorrection methods such as buffer zone, bordermethod, and weighting method (Moeur, 1993; Haase, 1995)since the plots in this study were all square orrectangular in shape, and were small in size.Thus, the toroidal edge correction method was used inestimating the parameters of the pair potential functions Φ (·).

Given a pair potential function, the Gibbspoint process models can be used to simulate anequilibrium point pattern.One of the methods wasoriginally developed by Metropolis et al. (1953), andmodified by Wood (1968). The algorithm is a MarkovChain Monte Carlo (MCMC)procedure and has beenapplied in many studies (Ogata et al., 1981; 1984;1985; Diggle et al., 1994), which is briefly describedin Appendix.

To evaluate thegoodness-of-fit for each model, 500 realizations of theGibbs models corresponding to each fitted pair potentialfunction were performed.Ripley's K-function (converted to L as $\hat L\left (d \right)= \sqrt {\hat K\left (d \right)/\pi } - d$)wascalculated for each realization, where d is the givendistance of magnitude between paired events. The 95% confident envelopes were constructed andplotted.Then, the observed L statistics from the datawere compared with the simulated 95% confidentenvelopes.If model fitting to the data was good, theobserved L statistics should lie within the simulated95% confident envelopes (Ripley, 1976).

The Gibbs point processmodels are fitted based upon detailed mapped data andindividual tree measurements of diameter and height.In forestry practice, however, it is difficult andexpensive to obtain these kinds of data.Therefore, it isdesirable to develop empirical regression models forpredicting the parameters of the Gibbs models using theavailable stand variables as predictors.Since most ofthe forest variables are highly correlated (e.g., treeDBH and height), the multicolinearity problem mayexist among the predictor variables.In this study, theprincipal component (PC)regression was used toovercome the multicolinearity problem (Neter et al., 1990).

The parameters of three pair potential functions, namely VSC [equation (4)], Diggle's [equation (5)]and Ogata and Tanemura's [equation (6)], wereestimated by the Takacs-Fiksel method (Diggle et al., 1994)for the 50 plots.The results of the goodness-offittest indicated: overall, 82%-84% of the 50 plotswere satisfactorily fitted by the Gibbs models with threepair potential functions (Tab. 2). The Diggle's pairpotential function performed best for the CSR plots.The VSC pair potential function performed best for theregular plots.The Ogata and Tanemura's pair potentialfunction was slightly better than the other two for fittingthe clustered plots (Tab. 2).

Tab.2 Summary of goodness-of-fit tests of spatial point patterns for the 50 plots

Tab.2 Summary of goodness-of-fit tests of spatial point patterns for the 50 plots Spatial point pattern Number of plots Unaccepted VSC Diggle Ogata & Tanemura Plot % Plot % Plot % CSR 24 3 12.5 0 0.0 1 4.2 Cluster 9 4 44.4 4 44.4 3 33.3 Regular 17 2 11.8 4 23.5 5 29.4 Total 50 9 18.0 8 16.0 9 18.0

The Gibbs model with the Diggle's pair potentialfunction [equation (5)] was selected as the spatialpoint process model since it had slightly bettergoodness-of-fit results among the three pair potential functions used in this study.

The Pearson correlation coefficients between thedependent variables (i.e., the estimated parameters $\hat \delta $ and $\hat \alpha $ of the Gibbs model with the Diggle's pairpotential function)and the available stand variableswere computed and tested for H₀: ρ_i=0. The correlation coefficients and the P-values of the testswere shown in Tab. 3. It was evident that both $\hat \delta $ and $\hat \alpha $ had significant correlations (P-value＜0.05)withmost of the stand variables.

Tab.3 Correlations among the two estimated parameters of Gibbs point process model with the Diggle's pair potential function and the available stand variables

Tab.3 Correlations among the two estimated parameters of Gibbs point process model with the Diggle's pair potential function and the available stand variables $\hat \delta $ $\hat \alpha $ Density/ (tree·m-2) Basal area/ (m-2·hm-2) Mean DBH/cm Mean height/m Mean crown length/m Mean crown width/m $\hat \delta $ 1 0.338 8 -0.640 9 0.334 1 0.719 4 0.705 9 0.504 7 0.273 0 (P-value) (-) (0.016 1) (0.000 0) (0.017 7) (0.000 0) (0.000 0) (0.000 2) (0.060 5) $\hat \alpha $ 1 -0.788 2 0.358 6 0.725 2 0.730 1 0.576 7 0.338 6 (P-value) (-) 0.000 0 0.010 6 0.000 0 0.000 0 0.000 0 0.018 6 Density 1 -0.541 5 -0.875 9 -0.891 8 -0.651 2 -0.473 2 (P-value) (-) 0.000 0 0.000 0 0.000 0 0.000 0 0.000 7 Basal area 1 0.698 7 0.660 1 0.598 5 0.197 3 (P-value) (-) 0.000 0 0.000 0 0.000 0 0.178 9 Mean DBH 1 0.968 6 0.734 1 0.407 1 (P-value) (-) 0.000 0 0.000 0 0.004 1 Mean height 1 0.681 4 0.379 4 (P-value) (-) 0.000 0 0.007 8 Mean crown length 1 0.236 5 (P-value) (-) 0.105 5 Mean crown width 1 (P-value) (-)

The ordinary least squares regression was firstused to regress the two parameters ($\hat \delta $ and $\hat \alpha $)on theavailable stand variables such as stand density, basalarea, mean diameter, mean tree height, mean crownlength, and mean crown width.It was found thatmulticolinearity existed among the predictor variables, especially among the mean tree diameter, mean treeheight, and mean of crown length (results notshown). Thus, principal component regression wasapplied to overcome the multicolinearity problem (Neter et al., 1990). The regression coefficients basedon the principal component regressions for predictingthe two parameters ($\hat \delta $ and $\hat \alpha $)of the Gibbs model onthe available stand variables were list in Tab. 4.Themodel R2 was 0.57 for theδ ^ model and 0.65 for the α^model.Therefore, the Gibbs model parameters can bepredicted using the two empirical regression modelswhen the values of the six stand variables are available (either observed or estimated).

Tab.4 Coefficients of empirical regression models for predicting the two parameters ($\hat \delta $ and $\hat \alpha $) of Gibbs point process model with the Diggle's pair potential function using the available stand variables

Tab.4 Coefficients of empirical regression models for predicting the two parameters ($\hat \delta $ and $\hat \alpha $) of Gibbs point process model with the Diggle's pair potential function using the available stand variables Dependent variable Intercept Density/(tree·m-2) Basal area/(m2·hm-2) Mean DBH/cm Mean height/m Mean crown length/m Mean crown width/m Fit statistics R2 P-value Diggle's $\hat \delta $ -4.215 7 0.286 2 -0.038 2 0.188 6 0.220 6 0.067 9 -0.117 4 0.572 < 0.000 1 Diggle's $\hat \alpha $ 0.920 8 -0.786 2 -0.009 4 0.015 0 0.027 9 0.064 0 -0.086 2 0.645 < 0.000 1

Based on the predicted parameters ($\hat \delta $ and $\hat \alpha $)ofthe Gibbs model with the Diggle's pair potentialfunction, the spatial point patterns of a plot can besimulated using the Metropolis algorithm.To evaluatethe performance of the two empirical regression modelsfor predicting the two parameters $\hat \delta $ and $\hat \alpha $, the Ripley'sK-function was used to compare the observed data andmodel prediction.First, the observed K-function wascomputed using the tree data for each of the 50 plots.Then, for each plot, a 95% confident envelope wasconstructed from 200 simulations using the predictedparameters of the Gibbs model obtained from the twoempirical regression models in Tab. 4.If the observedK-functions are within the 95% confidence envelope, the prediction of the Gibbs model parameters can beclaimed satisfactory.The results indicated that 100%of the CSR plots, 71% of the regular plots, and 56%of the clustered plots were predicted well by the twoempirical regression models.In total, about 81% ofthe plots were predicted satisfactorily by these models.

One plot from each of the three spatial pointpatterns was arbitrarily selected as the example to showthe application of the prediction models for the Gibbspoint process model.The estimated and predicted twoparameters ($\hat \delta $ and $\hat \alpha $)as well as the stand variables ofthe three plots were shown in Tab. 5.The estimatedtwo parameters were obtained from fitting the Gibbsmodel with the Diggle's pair potential function to thetree data of each plot.The predicted two parameterswere obtained from the empirical regression models in Tab. 4 using the observed values of the six standvariables of each plot.Then, the predicted parameters $\hat \delta $ and $\hat \alpha $ were used in the simulation process. Fig. 1, 2, and 3 illustrate 1)the observed versus simulatedRipley's K-functions, and 2)the observed versussimulated tree locations for the three example plots, respectively.The 95% confidence envelopes for thesimulated K-function were based on 200 simulationruns, while the simulated K-function curves shown inthe figures were randomly chosen from the 200simulations.

Tab.5 Estimated (Est.) and predicted (Pred.) parameters of Gibbs point process model with the Diggle's pair potential function for the three example plots

Tab.5 Estimated (Est.) and predicted (Pred.) parameters of Gibbs point process model with the Diggle's pair potential function for the three example plots Plot Spatial point pattern 05 Clustering 26 CSR 57 Regular Stand variables Density 0.720 0 0.402 4 0.755 1 Basal area 46.895 2 62.072 8 57.645 7 Mean DBH 8.553 5 13.035 0 9.140 5 Mean HT 9.607 4 12.911 0 9.526 8 Mean crown length 3.128 8 5.268 5 2.930 8 Mean crown width 1.114 4 1.389 0 1.194 4 Parameter Est. Pred. Est. Pred. Est. Pred. Diggle's pair potential function $\hat \delta $ -2.783 5 -1.985 8 -1.349 8 -0.969 3 -3.652 2 -2.316 0 $\hat \alpha $ 0.212 3 0.413 2 0.990 9 0.792 4 0.338 4 0.338 4

Plot 05 represents a clustered spatial pointpattern. The simulated Ripley's K-function onlypartially follows the observed K-function for plot 05.On the other hand, the simulated K-functions followthe observed K-functions quite well for both plot 26 (representing a CSR spatial pattern)and plot 57 (representing a regular spatial pattern), respectively. Nevertheless, the simulated tree locations look verysimilar to the observed ones for the three exampleplots. The overall patterns are reproduced successfullyfor the CSR, regular and clustered spatial patterns (Fig. 1, 2, and 3).

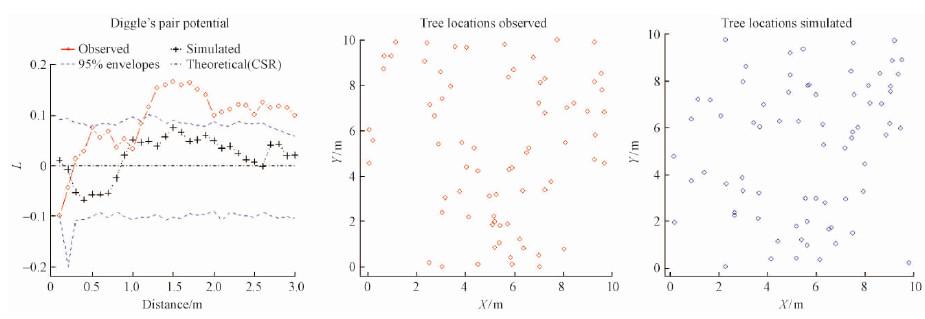	Fig. 1 Observed versus simulated spatial point patterns of plot 05 ( representing a clustering spatial point pattern)

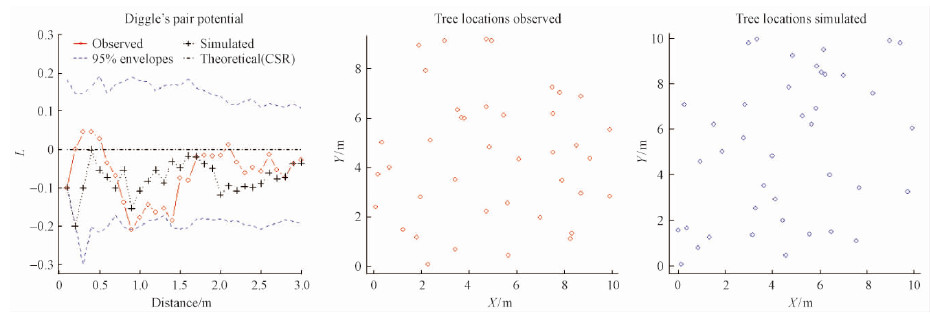	Fig. 2 Observed versus simulated spatial point patterns of plot 26 ( representing a CSR spatial point pattern)

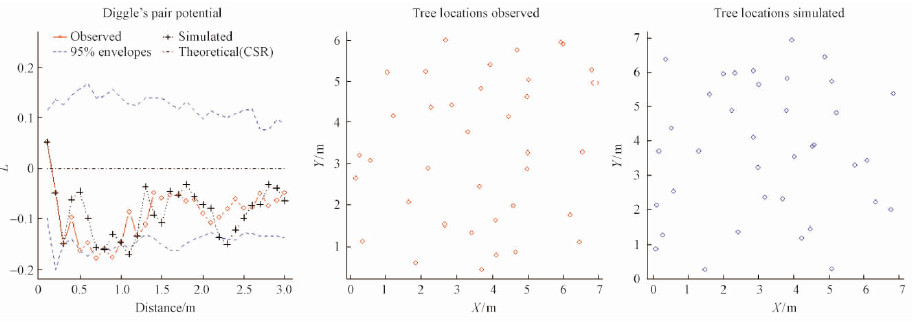	Fig. 3 Observed versus simulated spatial point patterns of plot 57 (representing a regular spatial point pattern)

In general, the Gibbs point process model withthree pair potential functions used in this studyperformed satisfactorily in modeling the spatial pointpatterns of trees within the 50 plots.The Diggle's pairpotential function had slightly better goodness-of-fitresults than the other two.However, for each spatialpoint pattern, the three models performed differently.The CSR and regular plots were modeled better thanthe clustered plots by all three pair potential functions.This finding is consistent with the findings in otherstudies using different spatial models (Stoyan et al., 2000). However, the shortcomings of this study were1)the size of the available spruce-fir plots wasrelatively small, 2)the number of plots for each of thethree spatial patterns (CSR, regular and clustering)was limited, and 3)there were no independent data orplots available for validating the empirical regressionmodels for predicting the two parameters of the Gibbsmodel.Therefore, more and large forest plots for eachpoint pattern, especially the clustered plots, may beneeded to further confirm and validate the results inthis study.

For estimating the parameters of the three pairpotential functions, the Takacs-Fiksel method wasemployed with arbitrary choices of the factors [such asL, m and rk in equation (8)].These factors may befurther evaluated by comparing the simulated spatialpoint patterns for the estimated pair potential functionsfrom different combinations of these factor values.TheMetropolis algorithm was utilized for simulating thespatial point patterns by the Gibbs point processmodels.Again, several factors [Δ, X (0), and T] were arbitrarily determined and may affect theconvergence to equilibrium and even the finalequilibrium state.These factors were not formallycompared with different choices in this study.However, the choice of T=1 000 seems sufficient forthese plots given the values of other factors (Δ=0.5 mand the initial state as a random pattern of a Poisson process).

In this study, the Gibbs point process modelswere applied to all spatial distributions of trees.It hasthe advantage of being flexible to fit various spatialpoint patterns.This is extremely useful if the spatialpattern of the data is not certain.Because of thisgeneral property, its performance varies amongdifferent spatial patterns.For example, in this study, it did not fit the clustered pattern as well as it fitted theCSR or regular patterns.In addition, the empiricalregression models for predicting the two parameters ofthe Gibbs models worked best for the CSR pattern, followed by the regular pattern, and worst for theclustered pattern.This was consistent with thegoodness-of-fit of the Gibbs point process models forthe spatial patterns.Therefore, it would be interestingto compare the model fitting and prediction, especiallyfor the clustered plots, using the Gibbs point processmodel against other spatial models such as Cox processmodel or Poisson cluster process model (Matern, 1971; Cressie, 1993)in a future study.

The Gibbs point process model with three pair potential functions were used to model the spatial pointpatterns of trees in the 50 spruce-fir plots in the Northeast, USA.The results indicated that the threepair potential functions fitted 82%-84% of the plotswell.The Diggle's pair potential function performedslightly better than the other two pair potentialfunctions (i.e., VSC and Ogata and Tanemura's). Ingeneral, the plots of CSR and regular patterns were modeled better than the clustered plots by all three pairpotential functions.Further, empirical regressionmodels were developed to predict the two parameters ($\hat \delta $ and $\hat \alpha $)of the Gibbs point process model with theDiggle's pair potential function using the availablestand variables as predictors (i.e., stand density, basal area, mean diameter, mean tree height, meancrown length, and mean crown width). The simulation results showed that 81% of the 50 plots were predictedsatisfactorily by these models, in which 100% of the CSR plots, 71% of the regular plots, and 56% of theclustered plots were predicted satisfactorily by theGibbs models.Three example plots were selected toillustrate that the patterns of the simulated treelocations were very similar to the observed ones.

The spatial structures of a forest stand include itshorizontal and vertical structures.The horizontalstructure can be characterized by the relative locationsof trees over space and the distributions of treediameters.The vertical structure can be represented bythe height distribution and diameter-heightrelationships.The spatial models developed in thisstudy can provide useful information on the horizontalstructures of forest stands, whereas the information onthe vertical structures of forest stands can be obtainedfrom a bivariate distribution model of tree diameter andheight.The combination of these models will offermuch more information on the three dimensional profileand dynamics of forest stands to forest managers andresearchers.

Suppose there are N trees on a plot A, assuming to have periodic boundaries (i.e., square or rectangular). These trees interact with each other according to a pair potential function, Φ (·) . Assume the state of the N-treesystem is X (t) = {X_i (t), i = 1, 2, …, N} at stage t, where x_i (t) is the ith tree's location on A. The total potentialenergy at the stage t is

$ {U_n}\left ( {X\left ( t \right)} \right) = - \sum\limits_{1 \leqslant i{\text{ < }}} {\sum\limits_{j \leqslant N} {\Phi \left ( {\left\| {X{{\left ( t \right)}_i} - X{{\left ( t \right)}_j}} \right\|} \right)} } $

Then, a trial state X' (t) = {X_i (t), i = 1, 2, …, N} is chosen such that a randomly selected tree X_r^* (t) isuniformly distributed within X_r (t)±Δ. It defines a small square centered at X_r (t) with side length Δ on A, whileall other trees keep their locations on A the same as at the state t. The total potential energy for the trial state is

$ {U_n}\left ( {X'\left ( t \right)} \right) = - \sum\limits_{1 \leqslant i{\text{ < }}} {\sum\limits_{j \leqslant N} {\Phi \left ( {\left\| {X'{{\left ( t \right)}_i} - X'{{\left ( t \right)}_j}} \right\|} \right)} } $

Compare U_n (X' (t)) with U_n (X (t)) as the following to decide the next state at stage (t + 1): (i) if U_n (X' (t))≤ U_n (X (t)), the next state X (t + 1) = X' (t), and (ii) if U_n (X' (t) ) ＞ U_n (X (t)) and if ξ ≤ exp［U_n (X (t))-U_n (X' (t))], where ξ is a random number uniformly distributed on (0, 1), the next state is X (t + 1) = X' (t) ;Otherwise, the next state is X (t + 1) = X (t). For a sufficiently large T, the state X (T) will be a realization ofequilibrium state under the Gibbs distribution characterized by the pair potential function Φ (·). The choice of Δ, initial state, and T affect the rate of convergence to the equilibrium． In this study, Δ was chosen to be 0. 5 m, theinitial state was a set of randomly generated locations of N trees on the plot A equivalent to a Poisson pattern, andthe maximum number of iterations T was set to 1 000．