文章信息
- 邵卓平, 吴贻军, 王福利
- Shao Zhuoping, Wu Yijun, Wang Fuli
- 竹材横向断裂的物理模型与能量吸收机制:基本组织开裂与界面脱粘
- The Physical Model and Energy Absorbing Mechanism of Bamboo Transverse Fracture:the Cracking of Parenchyma Tissue and Layering of Interface
- 林业科学, 2012, 48(7): 108-113.
- Scientia Silvae Sinicae, 2012, 48(7): 108-113.
-
文章历史
- 收稿日期:2011-06-24
- 修回日期:2011-11-28
-
作者相关文章
植物材料具有细胞组织结构的特殊性,其力学性能不仅与单细胞的力学性质有关,还与其组织结构的力学行为有着紧密的联系。竹子和树木是植物中能够用做结构材料的2种天然材料,经过数十亿年的物竞天择,各自形成了与其生存环境相适应的精细结构。与树木相比,竹子在力学性能上的显著优势在于高强高韧,其强度与韧性高于一般木材1~2倍(关锡鸿等,1987),但在组织结构上,竹的构造又较木材规则、简洁。因此,竹子更多地被人们用做仿生的范例加以研究,并在仿生材料的设计与制作上已进行了不同程度的尝试。如,仿竹纤维束梯度分布模式制成的碳纤维增强树脂材料与增强体均布材料相比其抗弯能力提高81%(周本濂,1995)、仿竹纤维以螺旋缠绕模型制备的材料与平直纤维材料相比其抗拉强度提高48%(李世红等,1991)。目前,以竹作为仿生优化模型的研究主要有2个方面(周本濂等,1994;张青等,2003):一个是对竹宏观形态的认识,如空心柱及增强相梯度分布;另一个是对竹纤维细胞壁微结构的认识,如微纤丝螺旋分布和多层结构。然而,竹作为纤维增强的胞体生物材料还有着丰富的细观构造特征,但多数研究并未就竹的组织结构与强韧功能的相互关系做细致的解析,而是将关注的重点集中在竹纤维细胞壁的结构上。实际上,纤维细胞壁的层级结构是所有植物纤维的共有特征,竹之所以具有高强高韧的力学性能,除了归因于纤维的优秀性质外,还源自于竹的完美的组织结构。但是,由于缺乏竹细胞及其界面的力学性质基础数据,使研究者迄今尚不能就细胞组织结构对竹材强韧化的贡献做出定量分析,影响了对纤维增强胞体材料仿生原理的深刻理解。目前国内外对竹材韧性研究几乎空白,文献检索仅见2篇文献(冼杏娟等,1991;Amada,2001),内容是采用金属材料断裂韧度试验方法测试竹材横向断裂韧性KIC,这是一种名义韧性,其意义有限,沈观林等(2006)指出类似纤维增强复合材料的横纹理断裂问题不宜采用应力强度因子法。竹材和木材在微观上同属由多层胞壁组成的胞体生物材料,但由于宏、细观构造上的不同使2种材料不仅在破坏机制上有所差异,而且在研究方法上也不相同。木材断裂在研究方法上是将木材视为宏观均质正交各向异性体,但竹材属纤维增强复合材料,其增强体具有明显非均匀分布的特征而不宜采用上述方法,因此须采用细观力学方法,通过建立细观模型的方法来研究竹材的断裂韧性。
1 竹材横向断裂的特征与能量吸收机制竹的节间细胞都是严格的轴向排列,没有木材中的横向射线细胞,因此,两节间的竹壁是典型的单轴向长纤维增强复合材料,其增强体纤维沿竹壁分布,外层致密,向内逐步变疏,由于竹细胞间的界面强度较弱,由此产生的强烈各向异性和纤维非均匀分布的结构特征,决定了其横断过程复杂。
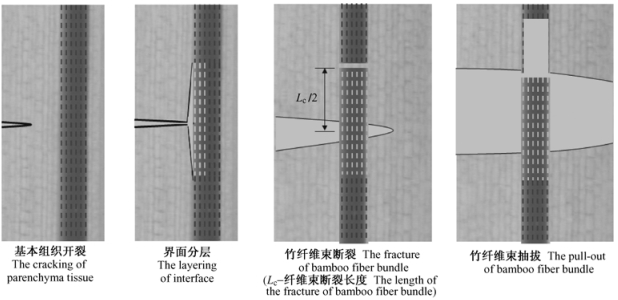
图 1是竹材去除竹青、竹黄后制作的含垂直纹理裂纹的三点横弯试件的试验简图,图 2是其断裂后的侧面图片,可见其断裂是由于多种失效的起始以及它们之间的相互作用。作为一种具有强烈结构特征的纤维增强材料,其性能和断裂破坏规律既取决于组分材料性质,也取决于其细观结构特征,这些特征包括竹纤维的体积分数、分布规律、形状以及纤维束与基体间界面的性质等。通过进一步对竹材试件横弯断裂的动态观察,其断裂破坏的总体发展过程可以描述为:首先是基体开裂,在裂纹尖端发展到竹纤维束时即折向界面,沿纤维束半围圈界面向两侧的开始分层开裂,界面裂纹扩展到一定长度,近半侧脱离基本组织簇拥的纤维束将在薄弱处或缺陷处断裂(此时层裂长度即为竹纤维束的断裂长度LC),该纤维束所受的载荷转移到附近材料,引起内应力的重新分布;最后断裂纤维束从断裂面的一侧被抽拔出来(图 3)。需要指出的是,在裂纹尖端遇到竹纤维束时,裂纹并不会越过纤维束向前扩展形成“纤维桥”,而是连带周围基本组织共同向两侧寻找最低的能量通路沿着弱的界面传播。但无论怎样,竹材试件在整个横弯断裂过程中至少包括有基本组织开裂、界面分层、竹纤维束断裂、竹纤维束抽拔等多种损伤模式,因而会有多种能量吸收机制,如果以形成单位裂纹面积所吸收的能量来表征竹材抗横断的断裂韧性G,则G可用下式表示:
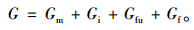
|
(1) |
|
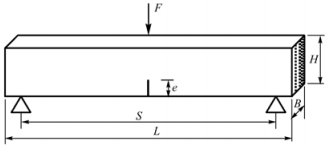
图 1 竹材SEB横断试验 Fig.1 Diagram of bamboo SEB transverse test |

|
图 2 竹材I型LT裂纹在竹壁内侧的扩展方式 Fig.2 Expansion pattern of model I LT crack in inner-layer 在竹壁内侧竹肉处,先基体-纤维界面损伤、脱离,继而纤维束断裂,裂纹近似自相似扩展。 In inner-layer, interface of matrix-fiber damages and seperates, and then fiber bundle breaks. The crack is approximately self-similar expansion. |
|
图 3 竹材断裂过程中的失效模式 Fig.3 Failure modes of bamboo during fracture |
式中:Gm,Gi,Gfu,Gf分别为竹材在横断时因基体组织开裂、界面分层、竹纤维束断裂、竹纤维束抽拔时单位面积所吸收的能量。
显然,不同组成结构的失效模式在断裂过程中会因不同的能耗而具有不同的增韧贡献率,如果能够将竹材组成结构的力学功能有选择地模型化并给出相应的解析或数值解,即可找出导致优良强韧性能的主要结构因素,这些工作不仅有助于揭示竹材的细观增韧机制和破坏机制,而且对研发具有特殊强韧性能的新型复合材料有重要指导意义。目前已有大量工作关于纤维增强复合材料在断裂过程中对应不同失效方式而建立的细观力学模型(Outwater et al., 1969;Cooper et al., 1970),虽然人工材料与天然复合材料在组成、构造等方面存在较大差异,但上述研究方法和途径非常值得我们借鉴。本文即针对竹材在横断过程中对应不同失效方式而建立的细观力学模型,应用解析法导出了基本组织开裂和界面脱粘分离时的能量释放率。
2 竹材韧性断裂过程中基本组织断裂和界面分层的能量释放率 2.1 对增强体的力学简化从力学的角度来考虑,可以把竹壁细胞分成两大类:一类是组成维管束的厚壁细胞竹纤维,起着增强体的作用;另一类是以基本组织为主的薄壁细胞,它们在维管束之间起着传递载荷和缓冲作用,其余为少量的疏导组织。竹纤维多存在于维管束的纤维鞘或纤维股中,以保护输导组织。由于竹材在受力时常以维管束一体的形式断裂破坏,为便于建模分析,可将整个维管束简化为空心圆环状的增强体(在本文仍称纤维束),其外径Df=2Rf和内径df=2rf可通过实测横截面上所有维管束的大小外、内径再平均算得。
2.2 基本组织的变形和开裂基本组织的变形和开裂易发生在竹壁内侧基本组织体积分数Vm较大的区域。由于竹纤维束强度比基本组织强度大得多,基本组织受载时在应力集中的区域(如裂尖前端)发生损伤,形成裂尖损伤区,微裂纹在该损伤区内萌生、长大、合并贯通、主裂尖前扩,在这种情况下,裂纹基本上沿垂直纤维束方向呈自相似扩展,因产生的新表面积较小,能量消耗很小。只有当基体裂纹遇到竹纤维束,裂纹沿竹纤维束和基体的界面通过分叉、平行于纤维束向前扩展时,断裂损伤过程中消耗的能量才有所增加。
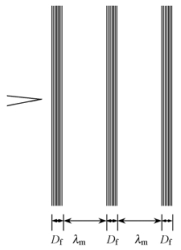
可以用一个二维模型(图 4)来计算基本组织的断裂功,假设竹材的基本组织与竹纤维束的平均线密度分别为λm和Df、竹基本组织体积分数和竹纤维束体积分数分别为Vm和Vf,由几何关系可知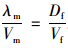
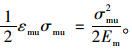
|
(2) |
|
图 4 基本组织开裂模型 Fig.4 Cracking model of ground tissue |
因此,竹材试件在横断过程中,基本组织对形成单位裂纹面积所吸收的能量为:
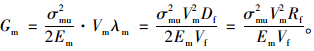
|
(3) |
式中:Em为竹基本组织弹性模量;σmu和εmu分别为基本组织断裂时的应力和应变。
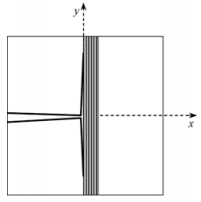
2.3 界面脱粘分离断裂理论表明,不管裂纹的大小和加载方式如何,在紧靠裂纹尖端区域的应力分布形式相同,而且在裂尖前方(1~2个原子以外)的一个较大区域中,不仅存在与裂纹表面垂直的拉应力σy,还存在与裂纹表面平行的拉应力σx(图 5),且在裂尖附近的应力比σy/σx在1~5之间。竹材纤维束抗拉强度很大,而组织间的界面强度很小。毛竹材沿顺纹理方向的拉伸强度可高达260 MPa,但沿横纹理方向的拉伸强度和顺纹理方向的剪切强度仅为顺纹理方向拉伸强度的1/85和1/20(曾其蕴等,1992)。因此,当裂纹尖端扩展到纤维束边界时,在平行裂纹表面的拉应力σx作用下纤维束和基本组织之间易发生分离。
|
图 5 界面分层开裂模型 Fig.5 Cracking model of interfacial delamination |
竹纤维束与基本组织脱粘分离发生在纤维束断裂之前,由于竹纤维束与基本组织间的界面强度以及基本组织间的界面强度均较弱,纤维束和基本组织之间的分离容易牵带周围基本组织间沿界面纵向分离,在纤维束附近的局部层面形成一个和原有裂纹相互垂直的侧裂纹,不仅纯化和抑制了原裂纹扩展,而且沿界面的层间裂纹还会吸收多余的应变能。由于竹材可近似视为长纤维增强复合材料,可以借鉴Willanms(1988;1989)、Wang等(1992)、Reeder等(1990;1991)、杜善义等(1998)等在分析和计算此类材料中各种不同类型脱层所对应的应变能释放率所做的研究工作。
图 6为竹试件层间裂纹尖端受载与转角分析示意图,设梁(或板)的厚度为H,宽度为B,含有一贯穿的层裂区域,载荷在梁的宽度方向上均匀分布,脱层上、下梁的厚度为h1和h2,作用力矩分别为M1和M2,E为梁的弯曲弹性模量。当脱层尖端由A-A截面扩展δa至B-B截面时,整个系统能量释放率为:
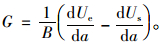
|
(4) |
|
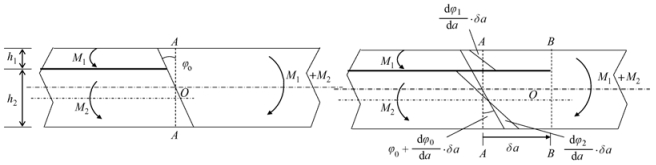
图 6 竹材层间裂纹尖端受载与转角示意 Fig.6 Sketch of wood beam interlaminar fracture a.分层裂纹尖端A-A截面的转角The coner of sectional A-A at interlaminar crack tip;b.分层裂纹尖端由A-A截面扩展δa至B-B截面时,A-A截面和脱层上、下层的转角While sectional A-A expanding to B-B whit δa, the coner of sectional A-A and coner between superstratum and lower layer. |
式中:Ue为外载对系统所做的功;Us为系统的应变能。
假设没有分层开裂,在载荷作用下,A-A截面的转角为 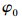
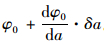
有分层开裂时,分层裂纹尖端A-A截面在载荷作用下的转角仍为 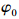
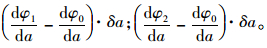
|
(5) |
根据弹性梁理论,各转角与作用力矩之间的关系为:
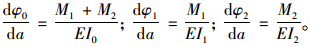
|
(6) |
其中截面惯性矩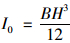
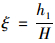
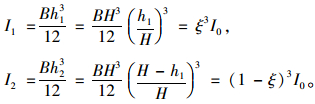
|
(1) |
于是,
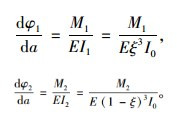
|
(7) |
当分层开裂存在时,层裂段上、下部分的转角与未分层开裂时的转角是不同的,这一转角差异,正是导致系统能量下降、成为层裂产生和扩展的的动力。因此,当层裂纹扩展δa过程中,外载所做的功的变化为:
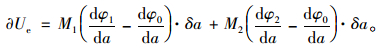
|
(8) |
将式(7) 代入式(8),即可得在层裂纹扩展过程中外力功的变化率为:
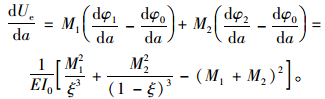
|
(9) |
同理,有层裂时的上、下部分梁段的应变能与未分层开裂时的系统的应变能是不同的,由弹性梁理论,可得系统应变能的变化为:
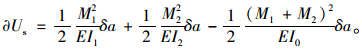
|
(10) |
于是可以得到在层裂纹扩展过程中系统应变能的变化率为:
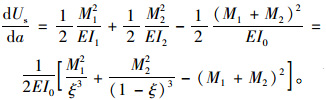
|
(11) |
所以,当脱层尖端由A-A截面扩展δa至B-B截面时,整个裂纹系统的能量释放率为:
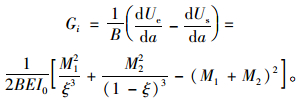
|
(12) |
如果结构存在垂直梁轴方向的横裂纹(图 7),图中e为横向裂纹长度,C为分层裂纹长度,S为跨长。显然,当竹梁试件受到三点弯曲承载形式时,只要取M1=0, M2=M=F(S-C)/4,代入式(12) 即可得到图示结构分层裂纹扩展的应变能释放率计算公式:
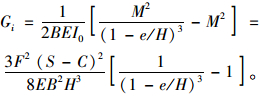
|
(13) |
|
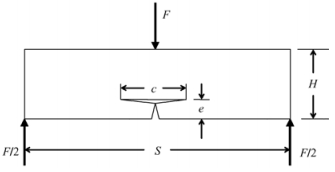
图 7 含垂直纹理裂纹的木梁分层开裂示意 Fig.7 Sketch of interlaminar fracture of wood beam containing crack perpendicular to grain |
分层裂纹扩展的应变能释放率会随分层裂纹长度C的增长而减少,当Gi低于材料的临界应变能释放率时,分层裂纹即停止扩展。特别,取C=0,即可以得到含垂直纹理裂纹的竹试件在承受弯曲载荷过程中,横向裂纹转侧向沿纹理方向启裂时的临界应变能释放率计算公式:
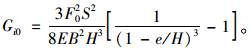
|
(14) |
式中:F0为顺纹理方向裂纹启裂时的载荷。
3 结论竹材试件在整个横弯断裂过程中至少包含有基本组织开裂、界面分层、竹纤维束断裂、竹纤维束抽拔等多种损伤模式,不同组织结构在损伤演化过程中会因不同的能耗而具有不同的增韧贡献。本文采用细观力学方法,研究了竹材在横弯断裂过程中基本组织开裂与界面脱粘这2种损伤模式的能量吸收机制,并推导得到这2种损伤模式的应变能释放率解析式,以及含垂直纹理裂纹的竹试件在承受弯曲载荷时、横向裂纹转向顺纹启裂时的临界应变能释放率解析式。
| [] | 杜善义, 王彪. 1998. 复合材料细观力学. 北京, 科学出版社: 161-237. |
| [] | 关锡鸿, 冼定国, 叶颖薇. 1987. 竹材—一种天然的复合材料. 复合材料学报, 4(4): 79–83. |
| [] | 李世红, 周本濂, 郑宗光, 等. 1991. 一种在细观尺度上仿生的复合材料模型. 材料科学进展, 5(6): 543–547. |
| [] | 沈观林, 胡更开. 2006. 复合材料力学. 北京, 清华大学出版社. |
| [] | 冼杏娟, 冼定国. 1991. 竹材的断裂特性. 材料科学进展, 5(4): 336–341. |
| [] | 张青, 戴起勋, 赵玉涛, 等. 2003. 仿生材料设计与制备的研究进展. 江苏大学学报:自然科学版, 24(6): 55–60. |
| [] | 曾其蕴, 李向红, 鲍贤镕. 1992. 竹节对竹材力学强度影响的研究. 林业科学, 28(3): 247–252. |
| [] | 周本濂, 冯汉保, 张弗天, 等. 1994. 复合材料的仿生探索. 自然科学进展—国家重点实验室通讯(6): 713–725. |
| [] | 周本濂. 1995. 复合材料的仿生研究. 物理, 24(10): 577–582. |
| [] | Amada S, Untao S. 2001. Fracture properties of bamboo. Composites Part B: Engineering, 32(5): 451–459. DOI:10.1016/S1359-8368(01)00022-1 |
| [] | Cooper G A, Kelly A. 1970. Mechanics of composite materials. London, Pergamon Press, Oxford. |
| [] | Outwater J O, Murphy M C. 1993. The influence of enviroment and class finishes on the fracture energy of glass-epoxy jionts. Proc 24th Conf SPI. |
| [] | Reeder J R, Crews J H. 1990. Mixed-mode bending methed for delamination testing. ALAA Journal, 28(7): 1270. |
| [] | Reeder J R, Crews J H. 1991. Redesigm of mixed-mode bending test for delamination toughness. Proc of ICCM-8 Section: 13–36. |
| [] | Williams J G. 1988. On the calculation of energy release rates for ceack laminates. International Journal of Fracture, 36(2): 101–119. DOI:10.1007/BF00017790 |
| [] | Williams J G. 1989. End corrections for orthotropic DCB specimens. Composites Science and Technology, 35(4): 367–376. DOI:10.1016/0266-3538(89)90058-4 |
| [] | Wang Y, Williams J G. 1992. Corrections for mode II freacture toughness specimens of composite materials. Composites Science and Technology, 43(3): 251–256. DOI:10.1016/0266-3538(92)90096-L |
 2012, Vol. 48
2012, Vol. 48
