森林火灾是一种自然灾害，主要与火险天气有关，这是决定防火季节开始和结束的主要依据。所谓火险天气就是利于森林发生火灾的气象条件，如降水、气温、空气相对湿度、风速等等，这些气象因子都能直接影响森林火灾的发生(张尚印等，2000；Pausas，2004)。因此，可以通过对这些气象因素的分析，找出有用的信息，为森林火险预报提供帮助。在美国、加拿大和澳大利亚等国发展了森林火险分级方法，通过对多种气象条件的分析确定火灾风险，为当地森林火灾的预报工作提供理论依据(Bradstock et al., 1998；Lee et al., 2002)。

我国学者对森林火灾和气象条件的关系也做了不少研究(宋卫国等，2006)。这些研究大都采用定向描述或简单的线性回归进行模拟分析。然而从林火发生次数的数据结构看，简单的线性回归已不能满足森林火灾的预报要求(郭福涛等，2010)。Poisson模型和负二项回归模型作为计数资料模型分析的基本方法应用广泛。而在实际问题研究中，又常常遇到观察事件发生数中含有大量的零，林火的月发生数正是属于多零现象(zero drived dispersion)，此时Poisson回归模型和负二项回归模型就无能为力了，有时即便强行实现，也会给分析结果带来失真的解释(曾平等，2008)。零膨胀负二项模型和Hurdle模型在于处理过离散数据时，能够解决零计数过多的问题。为此，考虑到林火数据结构特点，本研究基于黔南区春季防火期森林火灾发生次数和火险天气数据，采用Poisson回归模型、负二项回归模型、零膨胀负二项模型和Hurdle模型对林火发生次数进行模拟研究，着重介绍了零膨胀负二项模型和Hurdle模型，并对这些模型进行逐步筛选，找出最合适的模型，为黔南区森林火灾的预报工作提供理论基础。

1 研究区概况与数据来源 1.1 研究区概况

黔南布依族苗族自治州(黔南州)位于贵州省中南部，总面积2.62万km²，地理位置为25°04′—27°29′N，106°21′—108°18′E，行政所辖12个县市，分别为瓮安、福泉、贵定、龙里、长顺、惠水、都匀、平塘、独山、三都、罗甸和荔波。黔南州地势西北高、东南低，地貌类型多样，以山地为主。气候属亚热带季风湿润气候区，其特点是季风气候明显，四季分明，冬无严寒，夏无酷暑，降雨充沛，雨热同季，湿度较大，日照偏少，立体气候明显。多年平均气温稳定在13.6~19.6 ℃，大于10 ℃积温3 350~5 500 ℃，呈现南部高北部低、东部高西部低的分布特点。平均年日照1 100~1 300 h，无霜期240~320天，年平均降雨量1 100~1 400 mm，年平均相对湿度80%~83%。黔南州是贵州省重点森林火险区之一。全州历年来冬、春旱严重，往往冬旱连春旱、气候干热，高火险等级天气时间长，也是全省最先进入和最晚结束防火期的地区。

1.2 数据来源

本研究所用数据取自黔南地区12个县1996—2007年间1—4月春季防火期林火数据和气象数据。气象因子主要有月最高气温(T_max)，月平均最高气温(T_m)，月平均相对湿度(H_m)，月最小相对湿度(H_min)，月平均风速(S_m)，月最大风速(S_max)，月降雨量(R_a)和月蒸发量(E_v)。本研究利用上个月的气象数据预测下个月的火灾发生数，总共有432个样本数据，随机选取300个数据作为建模数据，其余剩下的132个作为模型检验数据。表 1为气象因子统计表。

2 数据分析 2.1 零数据分布

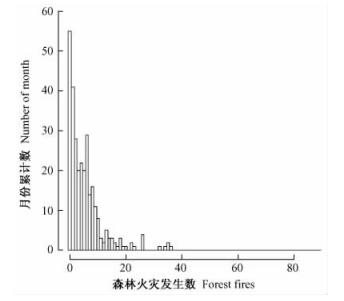
在本研究中，首先对黔南地区春季防火期森林火灾发生数进行简单分析，从直方图(图 1)可以看出，频数分布向左偏，共有55个月没有发生森林火灾，这也恰恰说明了林火数据中存在着大量的零数据。

2.2 多重共线性检验

本研究中，选取月最高温度、月平均最高温度、月平均相对湿度、最小相对湿度、月平均风速、月最大风速、月降雨量、月蒸发量8个主要气象因子来建立黔南区春季防火期森林火灾发生次数模型。为了提高参数估计的有效性，要尽可能去掉彼此间线性相关的气象因子，为此，在建模之前对所选的气象因子进行多重共线性检验。共线性检验指标有多个，本研究选取方差膨胀因子(VIF，variance inflation factor)。当方差膨胀因子(VIF)的值越大，说明自变量j与其他自变量间存在共线性的可能性越大。通常当VIF>10时，便认为变量X_j与其他变量之间存在多重共线性。根据表 2，VIF的取值最大都不超过4，因此，可以认为这8个气象因子间都不存在共线性。共线性检验的结果见表 2。

2.3 模型评价

为了比较Poisson模型、负二项模型、零膨胀负二项模型和Hurdle模型的拟合情况，通过绝对误差(Bs)和AIC值(akaike information criterion)统计量进行比较。此外，本文将选用Vuong(1989)的模型择优检验方法，Vuong在2个模型解释能力相等的假设下得到Z统计量并进行似然比检验，极大地提高了模型择优的效果。

(1)

(2)

式中，n为样本数，y_i为观测值，ŷ_i为预测值，N为模型中参数个数，LogL是以自然数为底的似然对数。本研究中，Poisson模型、负二项模型、零膨胀负二项模型和Hurdle模型的参数估计均在R统计软件中完成。

3 研究方法与结果

森林火灾的发生与火险天气密切相关，也就是与降水量、气温、空气相对湿度、风速等气象因子有关，本研究主要利用这些气象因子建立林火次数模型。

3.1 Poisson模型的拟合结果分析

Poisson回归模型是一种常用的离散数据计算方法(恽振先，1992；Bailer et al., 1997；Mandallaz et al., 1997)。由于Poisson模型和负二项模型比较常见，文中未一一列举。根据模型的参数统计t检验结果，剔除掉不显著的变量，最终得到Poisson模型的参数估计值及评价统计量(表 3)。

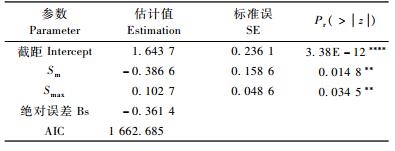
由数据分析得知，林火数据过于离散，由于Poisson回归均数和方差相等(equi-dispersion)的假设条件过于严格，使得Poisson回归模型不再适用，这时可以考虑下负二项模型。

3.2 负二项回归模型的拟合结果分析

负二项分布是一种离散型的分布，它是Poisson分布和对数分布2个基础分布的复合分布，主要用于描述超方差的事件发生频数的发生规律(Kagraoka，2005；Greene，2008；许飞，2009)。与Poisson模型一样，去掉不显著的变量，负二项模型的参数估计及评价统计量见表 4。

由表 3和表 4可以看出，Poisson模型的绝对误差为-0.417 1，AIC值为2 537.669；负二项模型的绝对误差为-0.361 4，AIC值为1 662.685。因此，相对于Poisson分布，负二项分布拟合效果应该比较好(McCullagh et al., 1989)。另外，Vuong检验的检验值为-7.087 166，P值为6.844 29E-13＜0.000 1，效果显著，说明负二项分布模拟效果优于Poisson分布。

负二项分布与Poisson分布不同的地方就是多1个离散参数，它能够解释数据的离散程度，因此，它比Poisson分布更具有适用性(MacNeil et al., 2009)。虽然负二项模型比Poisson模型弹性好，但是对于零个数较多的数据，其拟合也不是很理想。

森林火灾发生的次数，并不是每月都发生，因此在统计每月发生次数时，就会有大量的零，由此带来数据的过度离散(zero drived dispersion)，此时Poisson回归模型和负二项回归模型就无能为力了，有时即便强行实现，也会给所分析的结果带来失真的解释。零膨胀负二项模型的优势在于处理过离散数据，能够解决零计数过多的问题，即数据中出现的异质性问题(方差大于均值)。

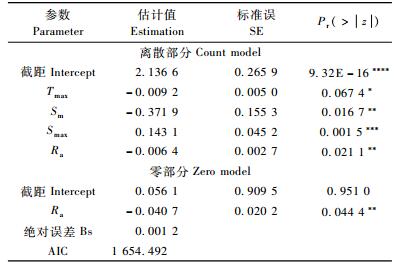
3.3 零膨胀负二项模型及拟合结果分析

零膨胀负二项模型就是为了拟合零过多数据而发展起来的(Lambert，1992；Welsh et al., 1996)，它实际上是从零分段而建立一个混合的概率分布，它将观察数据分为结构零部分和离散部分并分别建立模型，从而处理事件发生数中过多零的问题。

在零膨胀负二项模型中，零数据有2个主要来源：一是那些从未可能发生的零部分；二是在Poisson或负二项理论分布下没有发生的离散部分(Eskelson et al., 2009)。对于零膨胀负二项模型中的离散部分类似于负二项模型，利用广义线性模型的方法估计参数，而对于结构零部分，Lambert(1992)提出利用logit函数进行连接。令logit(p)=A=δX_i，这样就确保估计出来的p较合理的。因此，零膨胀负二项模型为：

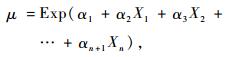
(3)

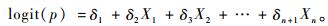
(4)

零膨胀负二项模型参数统计及模型评价见表 5。

由表 4和表 5可以看出，负二项模型的绝对误差为-0.361 4，AIC值为1 662.685；ZINB模型的绝对误差为0.001 2，AIC值为1 654.492。因此，相对于负二项回归，零膨胀负二项回归模型拟合效果比较好。另外，Vuong检验的检验值为-2.212 005，P值为0.013 483 15＜0.05，在0.05置信水平上效果显著，说明零膨胀负二项模型模拟效果优于负二项模型。

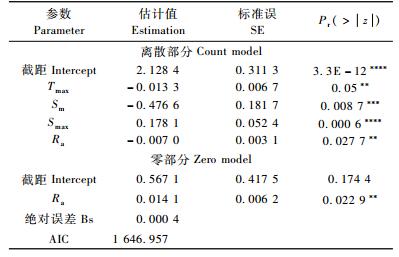
3.4 Hurdle模型及拟合结果分析

模拟多零数据的模型不止只有零膨胀负二项模型，Mullahy (1986)提出了Hurdle模型，该模型广泛应用于经济领域，是解决多零现象的又一个模型，而且模拟多零数据的结果也较好(Jones，1989；Moffatt，2005；Ground，2007)。Hurdle模型又叫Two-part模型(Cameron et al., 2005)，它分为2部分：一是截尾计数函数来模拟正的计数部分，如Poisson分布、几何分布或负二项分布等；另一部分是Hurdle部分模拟零个数。Hurdle部分函数可以是二项分布或者是截尾计数分布等。简单的Hurdle模型是将样本中所有零值从非零值中分离出来，在零处设定一个函数，对非零处过程用另一个函数确定。

由于模拟Hurdle部分和正的计数有多种概率函数，考虑到火灾数据结构的特点，研究利用负二项分布函数来描述。在Hurdle部分，令μ_1i=exp(x′_iγ₁)为负二项分布的期望。同样，在正的计数部分，令μ_2i=exp(x′_iγ₂)为负二项分布的期望。有指示函数：

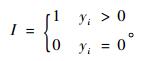
(5)

由概率函数可推导出这2部分的似然函数和Hurdle模型的似然函数：

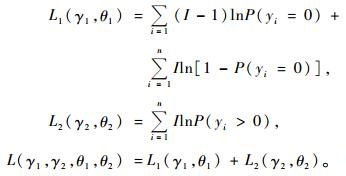
(6)

式中，L₁(γ₁，θ₁)为Hurdle部分的似然函数，L₂(γ₂，θ₂)为正的计数部分的似然函数。假设这2部分独立，那么Hurdle模型的极大似然值就是这2部分的极大似然值之和。

上述4类模型，不管是回归参数或者是离散参数都是通过极大似然估计法估计出来(Cameron et al., 2005；Zeileis et al., 2008)，并均在R统计软件中完成。Hurdle模型的参数估计及模型评价见表 6。

由表 5和表 6可以看出，ZINB模型的绝对误差为0.001 2，AIC值为1 654.492；Hurdle模型的绝对误差为0.000 4，AIC值为1 646.957。因此，相对于零膨胀负二项回归模型，Hurdle模型拟合效果比较好。然而，Vuong检验的检验值为-1.207 364，P值为0.113 646>0.05，在0.05置信水平上效果不显著。另外，从模拟无发生林火的结果上看(表 7)，Hurdle模型拟合比ZINB模型拟合更精确。因此，综合这几类评价指标，Hurdle模型优于零膨胀负二项模型。

4 模型检验

根据选出的最优模型Hurdle模型，利用检验数据进行检验，得到如下结果，见图 2(实际值为森林火灾的实际发生数，预测值是根据Hurdle模型所拟合的森林火灾发生数)。由图 2可知Hurdle模型拟合的结果相对比较好。

5 结论

在黔南地区春季防火期火险天气下林火发生数属于多零(zero-inflated)现象，因此，对于一般的计数过程，用标准的泊松分布、负二项分布等常用的计数模型用来拟合不能得到比较理想的结果，而零膨胀负二项模型在处理这类问题时的拟合效果有明显改善。实例研究也表明零膨胀负二项模型拟合效果比Poisson模型、负二项模型拟合的效果好，与郭福涛等(2010)的结论一致。而且，本文所引入的Hurdle模型，在预测黔南地区春季防火期森林火灾发生数的精度比零膨胀负二项模型高，得到的Hurdle模型为：

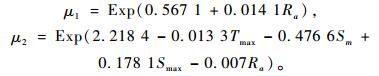
因此，相对于其他3种模型，利用Hurdle模型预测黔南地区春季防火期下月森林火灾发生次数，能够较好地为林火发生预报工作提供理论支持。但是，由于本研究周期为1个月，相对较长，若能获得旬的数据，Hurdle模型预测的效果应该会更好，那么黔南区火险天气森林火灾的预测精度将会大幅度提高。