林分生长和收获模型包括林分水平模型、单木水平模型。2类模型各有优缺点:单木水平模型可以直接判定各单株木的生长状况和生长潜力, 但是存在着复杂性、误差积累等缺点; 林分水平模型可以直接提供林分收获量, 但却无法反应林木水平的详细信息(Garcia, 2001; Qin et al., 2006; 孟宪宇, 1996)。

考虑到各类模型的优缺点, Bates等(1969)提出了组合预测方法(forecast combination), 开创了模型综合研究的先例, 并有效地应用于模拟预测。组合预测是将几种模型预测方法所得的预测结果选取适当的模型权重进行加权平均的一种预测方法, 该方法能够把不同模型的预测误差分散化, 充分利用单个模型的有效信息, 从而提高预测精度(Newbold et al., 2002)。常见的权重选取方法有标准差法、误差平方和法、方差协方差法、最优加权法等。组合预测方法特别是权重的选择在林分生长和收获模型研究中得到了广泛应用: 李际平等(2004)利用最优加权法确定权重, 对2个不同的林分材积模型进行组合预测, 提高了林分材积预测的精度; 张雄清等(2009)利用方差协方差法确定林分断面积组合预测模型的权重, 把通过单木水平模型和林分断面积模型所得的林分断面积预测值组合起来, 提高了林分断面积预测的精度, 同时也提高了林分断面积预测的兼容性。因此, 在组合预测中, 权重的选取对提高组合预测结果的精度至关重要; 然而, 不同权重计算方法组合模型的研究很少。

本文以北京山区油松(Pinus tabulaeformis)林为研究对象, 利用组合预测法对不同水平(单木水平、林分水平)所得的林分断面积进行组合预测, 然后通过误差平方和法、方差协方差法和最优加权法3种不同确定权重的方法进行比较, 最后确定最优的权重计算方法, 以提高林分断面积的预测精度。

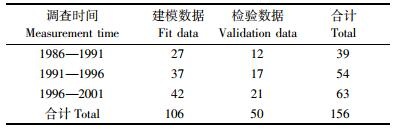
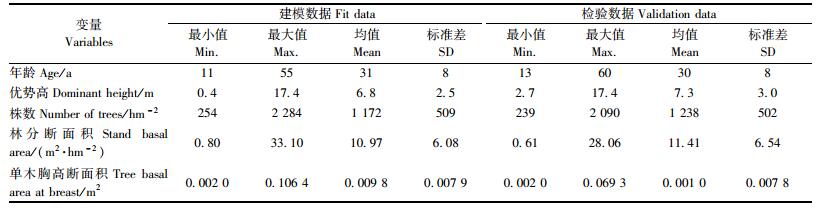
1 数据来源

本研究采用的数据来源于北京市林业调查设计院, 其中油松的固定样地63个, 每个样地面积为0.067 hm²。样地主要调查因子有:林木胸径、方位角、林分年龄、林分优势平均高、郁闭度、水平距、坡向、坡位、坡度、海拔、土层厚度等。样地每隔5年复测1次。本研究利用的数据是1986, 1991, 1996, 2001复测的一类清查数据, 1986年调查的样地有39块, 1991年调查的样地有54块, 1996年调查的样地有63块, 2001年调查的样地有63块。利用这些复测数据可以组成间隔调查期5年的样地有156块, 其中106块样地用于建模, 50块样地用于模型检验。油松林分样地分布情况及变量因子统计量分别见表 1, 2。

2 研究方法 2.1 组合预测权重确定的方法 2.1.1 误差平方和法

Newbold等(1974)提出在单个预测模型之间不存在相关性的前提下利用误差平方和法确定组合预测模型的权重, 预测精度较高; Winkler等(1983)研究表明:误差平方和法在对实际问题的预测研究中具有很好的预测精度。其原理为:对误差平方和小的模型赋予较大的权重, 误差平方和大的模型赋予较小的权重。权重公式为:

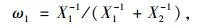
(1)

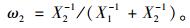
(2)

则林分断面积的组合预测模型为:

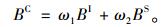
式中: ω₁, ω₂分别为单木水平模型和林分水平模型权重因子; X₁, X₂分别为单木水平模型和林分水平模型的林分断面积残差平方和; B^C为组合预测模型的林分断面积预估值; B^I为单木水平模型的林分断面积预估值; B^S为林分水平模型的林分断面积预估值。

2.1.2 方差协方差法

Bates等(1969)在提出组合预测方法的同时, 利用方差协方差法来确定组合预测的权重。方差协方差法利用加权平均的方法, 对较精确的预测值赋予较大的权重。这种方法从理论上得到最佳的权值系数组合, 如果这个权值可以保持稳定, 则此方法就有较大的稳定性; 但是在实际情况下权值常不稳定, 因此有局限性(张艳等, 2006)。单木水平模型和林分水平模型的权重分别为(Granger et al., 1977; Yue et al., 2008) :

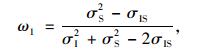
(3)

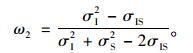
(4)

式中: σ_I²为单木水平模型林分断面积的残差的方差; σ_S²为林分水平模型林分断面积的残差的方差; σ_IS为这2种水平模型林分断面积的残差的协方差。

2.1.3 最优加权法

最优加权法实质为依据某种最优准则(如最小二乘准则、极小极大化准则等)构造目标函数, 在约束条件下使目标函数极小化, 求得组合模型的权重系数(唐小我, 1992)。最优加权法能够去除单项预测在组合预测模型中有偏的影响, 从而使得组合预测达到无偏(Jeong et al., 2009)。在本研究中, 根据最小二乘法原则, 构造目标函数。目标函数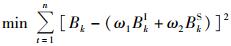, 约束条件ω₁ + ω₂ = 1。式中: B_k为第k个样地林分的每公顷胸高断面积。

针对该二次规划模型, 运用矩阵的计算可以简化这种模型的计算。记W = (ω₁, ω₂)^T, R =(1, 1)^T, e_i = (e_i1, e_i2, …e_in)。式中: T表示转置; W表示组合预测加权系数列向量; R表示元素全为1的n维列向量; e_i表示第i种预测模型的预测误差向量; n为样地数; i = 1, 2, 即单木水平模型和林分水平模型。

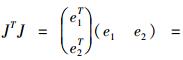
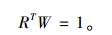
令J = (e₁, e₂), 则。用Z表示林分断面积预测的误差平方和, 则Z = W^TEW。由约束条件ω₁ + ω₂ = 1, 可以得到:

(5)

那么求解林分断面积最优组合预测模型的任务就是在式(5)的约束下, 求权重向量W, 使组合预测的误差平方和Z达到极小。引入拉格朗日乘数λ后, Z可以表示为(王建平, 1993; 陈友华, 2008) :

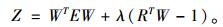
要使Z取极小值, 则Z的一阶偏导:

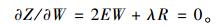
(6)

由式(5), (6)可解得权重向量:

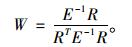
(7)

式中: E^-1为逆矩阵。利用ForStat软件(唐守正等, 2009)就可以计算出2个不同水平模型的权重系数。

2.2 单木胸高断面积模型及林分断面积模型的建立

Cao(2002)在对单木生长模型进行年生长预测时, 提出了可变生长率法(variable rate method), 该方法考虑了单木每年生长的变化, 而不是按每年固定生长率进行的。那么, 林分每年的生长量也是有变化的, 不应该固定不变。

本文利用可变生长率法, 对林分优势高方程、林分株树密度方程、林分平方平均直径方程、林分断面积方程、单木胸高断面积生长方程、存活率方程(Cao et al., 2008)的推导如下:

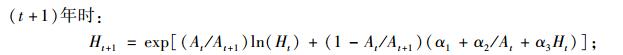
(8a)

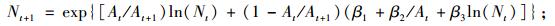
(8b)

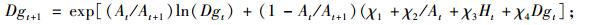
(8c)

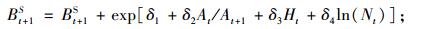
(8d)

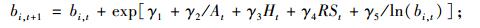
(8e)

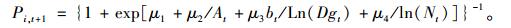
(8f)

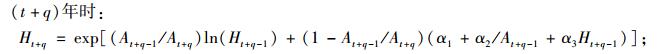
(9a)

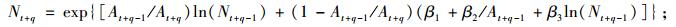
(9b)

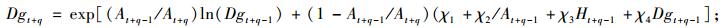
(9c)

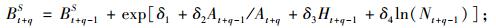
(9d)

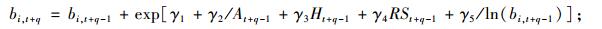
(9e)

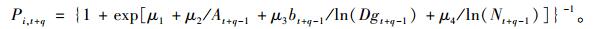
(9f)

式中: RS_t为相对植距指标，RS_t =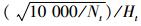; q为生长期(调查间隔期，5年); A_t为t年时林分的平均年龄; H_t为t年时林分的优势木平均高，m; N_t为t年时林分的公顷株树，株·hm^-2; Dg_t为t年时林分平方平均直径，cm; B_t为t年时林分断面积，m²·hm^-2; b_i，t为t年时单木胸高断面积，m²; P_{i，t + 1}为t年时存活的第i株林木在(t + 1)年时的存活率; α₁，α₂，…μ₄为待估参数。

根据方程(9e)，可以得出第2期单木的胸高断面积预估值，然后结合单木存活率预测方程，就可以计算出第2期林分断面积预估值, 也就得到了单木水平的林分胸高断面积预估值B^I。

由于上述各类模型之间存在着一定的相关性, 本研究对上述(9a ~ 9e) 5个方程采用似乎不相关联立估计方法(SUR)估计参数。本研究参数估计、模型评价均利用SAS软件来完成(高惠璇, 1997)。

3 模型评价

林分断面积生长模型、单木胸高断面积生长模型和单木存活率方程等可以通过统计量平均绝对误差(MAD)、均方根误差(RMSE)和决定系数(R²)、对数似然值(lg L)进行评价。它们的数学表达式分别为:

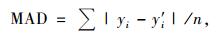
(10)

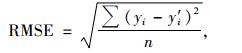
(11)

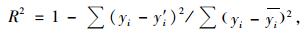
(12)

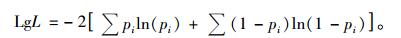
(13)

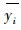
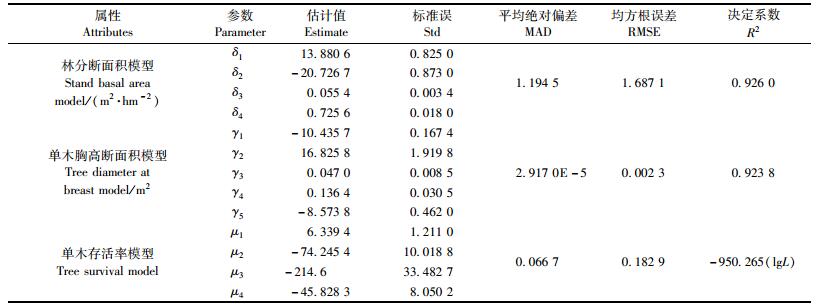
式中: y_i为实际值(林分断面积、单木胸高断面积、单木存活率); y'_i, 分别为它们的预测值和平均值; p_i为单木存活率; n为观察个数。

4 结果与分析

各类生长模型的参数估计值、标准误及模型评价统计量见表 3。由表 3的参数标准误可知:这几个模型的参数估计值都有效, 参数比较稳定。从表 3还可知:林分断面积生长模型的MAD为1.194 5 m²·hm^-2, RMSE为1.687 1 m²·hm^-2, R²为0.926 0;单木胸高断面积生长模型的MAD为2.917 0E-5m², RMSE为0.002 3 m², R²为0.923 8;单木存活率模型的MAD为0.066 7, RMSE为0.182 9, lgL为－ 950.265。经过Kolmogorov-Smirnov正态性检验, 林分断面积生长模型的残差、单木胸高断面积模型的残差均服从正态分布。

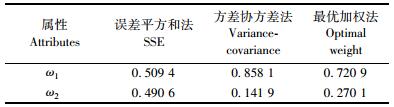
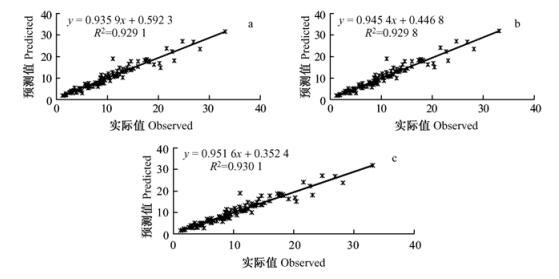
表 4列出了3种不同方法所确定的权重系数。根据这些权重系数可以计算出各种方法所得权重的组合林分断面积预测值, 并求出评价各种权重的统计量(表 5)。由表 5可知:不管是组合预测中的哪种权重确定方法, 组合预测的精度都比单个水平模型的精度高; 而且, 在这3种方法中, 误差平方和法的精度最低, 方差协方差法次之, 最优加权法的精度最高。由图 1可知:最优加权法的林分断面积预测值与实际值线性相关比其他2种方法显著, 精度高。

表 6列出了利用检验数据所得的各种不同模型的评价统计量。由表 6可知:在检验数据中, 组合预测法的精度比单个水平模型的精度高, 而且利用最优加权法所预测的林分断面积精度比方差协方差法、误差平方和法高, 这与表 5得出的结论一致。因此, 利用最优加权法确定林分断面积模型的权重系数, 相对于其他2种方法预测精度较高, 效果较好。

5 结论

组合预测方法能够充分利用单个预测模型的有效信息, 使单个模型之间优势互补, 分散预测误差, 提高了模型的精度。本研究实例中也证明了不管是组合预测中的哪种权重确定方法, 组合预测的精度都比单个模型的精度高, 这与张雄清等(2009)所得结果一致。在本研究所利用的误差平方和法、方差协方差法和最优加权法3种权重确定方法中, 最优加权法预测的精度最高(R² = 0.929 2, MAD = 1.132 0), 其次是方差协方差法(R² = 0.929 1, MAD = 1.133 4), 误差平方和法预测精度最低(R² = 0.928 9, MAD = 1.135 9)。因此, 利用最优权重加权法计算林分断面积组合预测模型的权重最优。