文章信息
- 张雷, 刘世荣, 孙鹏森, 王同立
- Zhang Lei, Liu Shirong, Sun Pengsen, Wang Tongli
- 基于DOMAIN和NeuralEnsembles模型预测中国毛竹潜在分布
- Predicting the Potential Distribution of Phyllostachys edulis with DOMAIN and NeuralEnsembles Models
- 林业科学, 2011, 47(7): 20-26.
- Scientia Silvae Sinicae, 2011, 47(7): 20-26.
-
文章历史
- 收稿日期:2010-12-11
- 修回日期:2011-05-19
-
作者相关文章
2. 中国林业科学研究院 北京 100091;
3. Department of Forest Sciences, University of British Columbia Vancouver V6T 1Z4
2. Chinese Academy of Forestry Beijing 100091;
3. Department of Forest Sciences, University of British Columbia Vancouver V6T 1Z4
物种分布模拟模型又称为生态位模型, 其本质是在物种分布区与环境之间建立相关关系。物种分布模型在珍稀濒危物种管理、外来种入侵扩散监测、生物多样性保护、气候变化对物种分布的潜在影响评估方面应用广泛。随着计算机和统计学的发展, 开展了大量有关物种分布的模拟模型研究。目前对物种分布的模拟, 主要集中在3个层面(Elith et al., 2006) : 1)只利用物种分布存在数据对单个物种进行模拟; 2)同时利用物种分布存在和分布不存在数据对单个物种进行建模; 3)模拟物种丰富度。根据对物种分布数据的需求, 可将物种分布模型分为2类:一类是针对物种分布存在数据的模型, 称为概形分析模型(profile techniques), 这类模型基于环境阈值(environmental envelope)或距离(distancebased)来预测物种分布, 目前常用的此类模型有BIOCLIM (Nix, 1986), HABITAT (Walker et al., 1991), DOMAIN (Carpenter et al., 1993), Biomapper (Hirzel et al., 2002), Maxent (Phillips et al., 2006)和GARP (Stockwell, 1999)等; 另一类是同时利用物种分布存在和分布不存在数据的模型, 以及利用物种丰富度数据的模型, 它们统称为分类判别分析模型(group discrimination techniques), 属于这类的模型比较多, 且以统计建模为主, 常用的分类判别分析模型有GRASP (Lehmann et al., 2002), PresenceAbsence (Freeman et al., 2008), BIOMOD (Thuiller, 2003), openModeller (Souza Muoz et al., 2009), NeuralEnsembles (O'hanley, 2009)和SAM (Rangel et al., 2006)等。
在近期的物种分布模拟研究中, 学者逐渐由应用概形分析模型转向了应用分类判别分析模型, 这是由于概形分析模型中没有物种分布不存在数据对模型预估进行限制, 因此概形分析模型通常偏大估计物种分布区(Elith et al., 2006; Barry et al., 2006; Chefaoui et al., 2008)。在应用分类判别分析模型时, 经常遇到的问题是缺少物种分布不存在数据, 这是由于物种分布数据多来自标本馆、博物馆和物种图集, 只有物种分布记录。而在建模过程中通常采用的方法是随机产生虚拟的物种分布不存在数据(pseudo-absences)作为“真实”的物种不存在数据(Chefaoui et al., 2008; Václavík et al., 2009), 然而, 无物种分布记录的地区不等于物种绝对不适宜生存, 这是由于历史或者生态的原因, 适生区的物种可能受到了破坏。因此虚拟分布不存在数据可能会影响模型的预估能力, 尤其是对于物种分布记录稀少的稀有物种的影响更大, 对于广布种的影响可能较小, 广布种大量的物种分布存在数据可能会抵消错误选择的物种分布不存在数据的影响。
毛竹(Phyllostachys edulis)是我国分布最广、面积最大、经济价值最高的竹种之一, 是中国南方重要的森林资源。同时毛竹林作为异龄林, 具有生长速度快、产量高、可以隔年连续采伐及永续利用等特点, 因而毛竹林具有重要的碳汇作用(周国模, 2006)。首先利用DOMAIN模型生成物种生境适宜性分布图, 选取低生境适宜性的地区作为“真实”物种分布不存在区, 然后随同物种分布存在数据一起输入到NeuralEnsembles模型中进行我国毛竹在当前和未来气候条件下的潜在分布模拟, 同时分析分布不存在区数据取样数量对模型预测能力的影响, 以进一步揭示建模数据与模型预测精度的关系, 对于更有效地利用物种分布模型, 增加模型预测的可靠性具有重要意义。
1 数据来源及处理 1.1 毛竹地理分布数据毛竹现实空间分布数据从中国科学院植物研究所编制的1: 100万植被图中提取。植被图基本反映了20世纪80和90年代的植被分布现状(中国科学院中国植被图编辑委员会, 2001)。植被图数据来源于国家自然科学基金委员中国西部环境与生态科学数据中心(http://westdc.westgis.ac.cn)。植被图中标识有毛竹分布的地方(包括毛竹纯林或毛竹混交林), 均视为适宜毛竹分布地区。植被图中毛竹分布数据为矢量格式, 因此需要对其进行栅格转换, 栅格分辨率定义为8 km, 转换后得到毛竹分布栅格单元数据点共计961个。
1.2 气候变量本研究采用9个具有明显生物学意义的气候预测变量(年平均气温、平均最冷月气温、平均最暖月气温度、气温年较差、平均年降水量、平均夏季5—9月降水量、<0 ℃年积温、>5 ℃年积温和>18 ℃年积温)。本文采用的未来气候数据由政府间气候专门委员会(IPCC)排放情景报告(SRES)中推荐的A2情景下的挪威大气环流模型BCCR-BCM2.0 (bjerknes centre for climate research)产生。本研究采用双线性插值和动态海拔调整技术(Wang et al., 2006), 对1961—1990年PRISM (Daly et al., 2002)数据进行降尺度处理得到当前基准气候(1961— 1990)条件下30年的气候数据平均值, 也对大气环流模型BCCR-BCM2.0进行降尺度处理得到未来3个时间段(2010—2039, 2040—2069和2070— 2099) 30年的气候平均值。降尺度处理后得到的是8 km分辨率的气候数据, 采用的地理投影坐标系统与栅格化的毛竹空间分布数据一致。
2 研究方法 2.1 DOMAIN模型本研究采用的DOMAIN模型通过DIVA-GIS软件(http://www.diva-gis.org/)来实现。DOMAIN模型的优点是只利用物种分布存在数据, 并且在预测变量较少时, 可以有效模拟物种的潜在分布(Carpenter et al., 1993)。DOMAIN模型是基于距离的模型, 基于临近空间环境的相似性, 利用Gower Metric(Gower, 1997)计算点与点之间的相似性, 利用点对点的相似矩阵对待估地点进行赋值。由于DOMAIN采用的是连续相似函数, 因此它在模拟物种分布时更具灵活性。DOMAIN定义的气候阈值空间是非连续的。DOMAIN模型的输出值不是概率估计, 而是分类置信度。DOMAIN需要一个自定义阈值把所有待估地点的相似性值转化为物种分布存在区和不存在区, 这个阈值一般根据专业知识或者主观判断, 因此缺乏客观性。如果有物种分布不存在数据, 可以更有效且客观地选定这个阈值。
2.2 NeuralEnsembles模型NeuralEnsembles (http://www.kent.ac.uk/kbs/documents/staff/ohanley/neuralensembles.html)是一个可以免费获取的物种分布模拟模型软件, 它通过人工神经网络(artificial neural networks, ANN)模型来估计物种的生境适宜性。ANN是一个非线性的统计模型, 在物种分布模拟研究中有着广泛且成功的应用(O' hanley, 2009)案例。与其他模型相比, ANN的主要优点有(O' hanley, 2009) :既可以处理连续变量又可以处理分类变量, 具有较高的模拟精度(尤其对于稀有物种和具有不完整分布记录的物种)。
与其他物种分布模型相比, NeuralEnsembles模型的最大特点是利用多个ANN子模型的组合方式(ensemble forecasting)来预测物种分布。虽然组合预测方法在物种分布模拟研究中还处于初期阶段(Araújo et al., 2007), 但是大量理论研究表明组合预测方法比单个模型具有优越性(如高精度) (Granitto et al., 2005)。NeuralEnsembles通过反复训练生成一套针对单个物种的ANN子模型, 然后利用一个逐步组合构建规则(Granitto et al., 2005)对ANN子模型进行组合集成, 即通过对单个ANN子模型进行逐步训练和集成以达到使整体组合预测最佳化, 随后预测物种分布。基本过程为: NeuralEnsembles模型通过自举法(bootstrap)为每个ANN模型产生独立的训练数据集。接下来, 单个模型不断训练直到当前组合预测和前一步的组合预测的差异达到近似最小值为止。在每一步逐步组合构建过程中, 只有当前ANN的权重得到了更新, 前面模型的权重保持不变, 当前模型训练完成后被组合到前面的综合模型中。ANN模型输出结果范围为0 ~ 1, 为物种分布存在的条件概率估计。NeuralEnsembles预测的输出结果有:组合模型产生的平均生境适宜性以及其标准差和95%的置信区间。
2.3 DOMAIN和NeuralEnsembles耦合模型由于NeuralEnsembles模型需要物种分布存在和不存在数据。由于没有物种分布记录的地区不能都归为物种不存在区, 为了增加NeuralEnsembles模型预测的可靠性, 我们利用DOMAIN模型生成物种分布不存在数据。具体过程为:首先, 利用DOMAIN模型根据物种分布存在数据预测物种当前的潜在分布区。由于物种已知分布存在点在当前潜在分布区中的最小预测值是1.0, 因此把所有地区生境适宜指数小于1.0的地区都划分到“真实”物种分布不存在区中。由于现实分布不存在区中有与分布存在区气候条件相似的部分地区, 因此用于NeuralEnsembles模型的“真实”分布不存在数据比现实分布不存在数据减少了1 415个栅格单元。然后, 把已知物种分布数据和随机选取的一定数量的DOMAIN模型生成的“真实”物种不存在数据输入到NeuralEnsembles模型中(下文简称耦合模型), 进行当前潜在分布的模拟和未来潜在分布的预测。
2.4 模型评估NeuralEnsembles通过自举法抽样建立ANN子模型, 剩余的数据称为范围外数据(out-of-bag data), 用于验证组合模型(O' hanley, 2009)。NeuralEnsembles采用2种方法来评估模型精度: kappa值和接受机工作特征曲线(receiver operator characteristic curves, ROC)下的面积(area under the curve, AUC), 并给出他们各自的95%的置信区间。此外还采用敏感度(sensitivity, 物种分布存在区被正确预测的比例)作为评价指标。由于AUC不受诊断阈值的影响, 因此目前被公认为是最佳的评价指标(Fielding et al., 1997)。AUC评价模型的标准是(Swets, 1988) :极好, 0.90 ~ 1.00;好, 0.80 ~ 0.90;一般, 0.70 ~ 0.80;差, 0.60 ~ 0.70;失败, 0.50 ~ 0.60。Kappa用于测试空间格局的相似性, 它的范围是0 ~ 1, 0代表观测值和预测值没有一致性, 1代表完全一致(Cohen, 1996)。Kappa的计算需要指定一个阈值把物种分布概率转化为二元值(物种分布存在和不存在), 而本研究采用的是使Kappa值最大时的阈值。Kappa值评估标准为(Monserud et al., 1992) :极好, 1.0 ~ 0.85;很好, 0.7 ~ 0.85;好, 0.55 ~ 0.7;一般, 0.4 ~ 0.55;失败, <0.4。
为了评估“真实”物种分布不存在数据取样数量对于模型预测能力的影响, 分别从DOMAIN生成的“真实”分布不存在数据中随机选取一定数量的分布不存在数据用于建模, 选取的“真实”分布不存在数据数量分别是毛竹分布存在数量(961个)的1, 10, 20, 30, 40, 50, 60, 70, 80, 90和100倍。为了评估耦合模型的预测能力(即通过DOMAIN选取“真实”不存在数据是否有利于改进模型预测精度), 本研究选取现实条件下物种分布不存在数据进行NeuralEnsembles模型构建及评估, NeuralEnsembles选取的现实不存在数据也分别是分布存在数据的1, 10, 20, 30, 40, 50, 60, 70, 80, 90和100倍。
2.5 毛竹分布区面积变化及其迁移由于NeuralEnsembles模型的输出为物种分布存在的条件概率值, 比较分布区面积变化需要一个阈值以区分物种分布存在区和不存在区, 本研究采用的这个阈值是接受机工作特征曲线中的敏感度和特异度(specificity, 物种分布不存在区被正确预测的比例)差异最小时的值。本研究通过计算毛竹分布区质心来比较毛竹分布区的迁移方向和距离。物种分布区质心通过ARCGIS中的“mean center”函数来实现。
3 结果与分析 3.1 模型预测精度评估利用DOMAIN模型生成的物种低适宜性地区作为“真实”分布不存在数据, 剔除不适宜物种分布土地利用类型后(如水体和沙漠), 总计得到约105 000个毛竹分布不存在栅格单元。在这些“真实”分布不存在数据中选取一定数量的不存在数据用于NeuralEnsembles建模, 其模型精度见图 1。同时也直接在毛竹现实分布不存在数据中选择一部分分布不存在数据进行NeuralEnsembles建模, 其模型精度见图 1(下文简称单一模型)。图 1表明:耦合模型的预测精度比单纯利用NeuralEnsembles模型的模拟预测精度高。此外, 耦合模型和单一模型的敏感度和AUC值均随着分布不存在数据取样数量增大而减小, 但它们分别都维持在0.90 ~ 0.93和0.95 ~ 0.98, 预测精度属于极好一类, 可以认为它们对分布不存在数据取样数量不敏感, 而最大Kappa值随着不存在数据取样数量的增加而逐渐下降, 在取样数量大于物种分布存在数量的50倍时, 耦合模型和单模型的Kappa值降落到0.4以下, 模型预测精度属于失败一类。
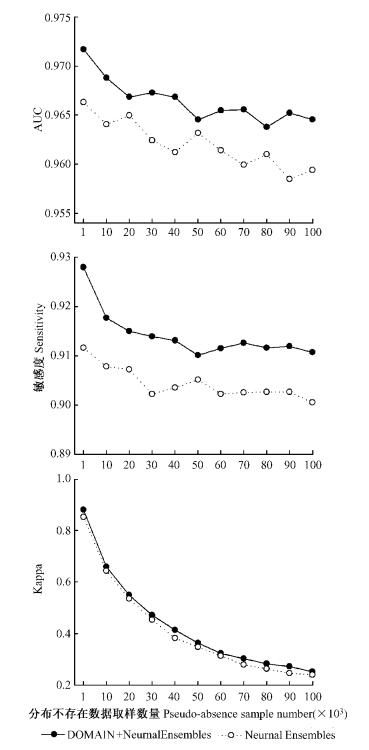
|
图 1 物种分布不存在数据取样数量对模型精度(AUC,Kappa和敏感度)的影响 Figure 1 Effects of pseudo-absence sample number on model predictive accuracy (AUC, Kappa and sensitivity) |
采用敏感度、最大Kappa值和AUC值都最大时建立的耦合模型模拟毛竹当前潜在分布, 预测未来气候变化对其潜在分布的影响。图 2表明毛竹当前主要分布在浙江、福建、江西、湖南、江苏南部、安徽南部、湖北东部, 四川中东部、广东和广西北部, 此外, 台湾北部也有分布, 主要集中在103°—122° E, 23°—32°N。

|
图 2 不同时期毛竹分布区 Figure 2 Phyllostachys edulis distribution in various periods |
气候变化对毛竹分布产生明显影响(图 2)。与1961—1990潜在分布相比:未来3个时期, 随着时间推移, 南部分布边界区(广东、广西北部分布区)逐渐向北退缩; 西部四川盆地适生面积逐渐减小, 至2079—2099时期, 只有盆地边缘区适宜生存; 贵州西部地区逐步转化为毛竹适生区; 东部沿海地区和台湾北部几乎没有变化; 毛竹北部分布区变化最为明显, 毛竹适生区逐步向北扩展。2010—2039和2040—2069时期江苏、安徽和湖北境内毛竹向北部迁移, 河南南部境内分布区增加。2079—2099时期, 东北平原、内蒙、山东和河北的部分地区甚至已经出现局部适生毛竹的潜在分布区。在未来的3个气候变化时期, 西藏错那县和墨脱县、新疆天山地区和内蒙五原县地区毛竹潜在适生区逐渐增加。总体而言, 毛竹当前的分布区逐步趋于破碎化, 出现局部不适宜毛竹生存的现象。
表 1表明:随着时间推移, 气候变化将导致毛竹分布区持续向北迁移, 迁移距离为33 ~ 266 km。尽管毛竹原适生区消失比例逐渐增大(3.8% ~ 23.7%), 但新适生区面积也逐渐增加(11.2% ~ 37.6%), 总体来看, 毛竹适生区面积逐步增加, 增加比例为7.4% ~ 13.9%。
|
|
本研究用于模型评估的3个指标表现不一, 这是由于AUC, Kappa和敏感度是3个不同原理的模型精度评估指标, 并且给不同的测量误差分配不同的权重。以敏感度为纵坐标, 以1减去特异度为横坐标绘制成的曲线称为ROC曲线, AUC是ROC曲线下的面积用于评估模型预测精度, ROC曲线利用所有可能的阈值把物种分布条件概率值转化为物种分布存在-不存在二元值以计算敏感度和特异度。Kappa值是敏感度、特异度、假阳性值(false positive, 1-特异度)和假阴性值(false negative, 1-敏感度)的函数, 它依赖物种分布存在和不存在转化阈值。本研究采用的是最大Kappa值, 即寻找一个分布存在和不存在转化阈值, 该阈值使Kappa最大。敏感度只针对物种分布存在数据, 它根据敏感度和特异度差值最小时的转化阈值计算物种分布存在区被正确估计的比率, 它是遗漏误差(omission error)的测量指标。把分布不存在数据取样数量转化为物种分布频率(prevalence or frequency of occurrence)后, 发现本研究和其他研究(Manel et al., 2001; Allouche et al., 2006)得出一致性结论: AUC值和敏感度都不受物种分布频率的影响, 而Kappa值对物种分布频率敏感。Allouche等(2006)发现Kappa值对物种分布频率响应形式为单峰曲线, 并且Kappa值在模型评估中引入了统计偏差, 建议不使用Kappa作为模型精度比较指标。
在没有真实的物种分布不存在数据的时候, 提高分类判别分析模型精度的有效方法是选取有效的物种不存在数据, 而产生有效的不存在数据的方法有很多, 如随机产生、通过概形分析模型产生, 根据与已知分布存在数据的距离产生等。例如: Vanderwal等(2009)在距离物种分布区不同距离范围内选取不存在数据, 进而评估模型预测能力, 发现距离物种分布区200 km的范围选取物种不存在数据用于建模构建最理想, 而来自较近或较远地区的物种不存在数据都会降低模型精度。但Chefaoui等(2008)发现利用环境空间上距离物种分布区较远地区选取的物种不存在数据建立的模型预测精度较高, 通过概形分析模型选择不存在数据建立的模型比随机选取不存在数据建立的模型预测精度高。本研究采用DOMAIN模型产生的物种分布不存在数据是一个有效的方法, 改进了NeuralEnsembles模型的预测精度。本研究也发现, 在分布不存在数据取样较少时, 耦合模型和单一模型预测精度都较高, 这可能是由于随机选取的物种分布不存在数据和存在数据之间的差异最大导致的, 随着取样的增加, 2者之间的差异可能逐渐减小, 从而导致模型对2者的识别率下降。本研究只探讨了根据一个阈值(即1.0)来区分DOMAIN预测图中物种存在区和不存在区的转化情况。在建立高精度的预测模型时需考虑如何选取分布不存在数据, 如对不存在数据进行分层取样是否有效?哪些方法是选取物种分布不存在数据的最有效方法?这些都需要进一步探讨, 以便提高模型对物种分布存在和不存在的识别率, 进而更有效地应用分类判别分析模型。
概形分析模型在物种分布模拟中出现偏大估计物种分布区的现象在以往研究中也有发现。例如: BIOCLIM模型采用环境阈值空间来预测物种分布, 而现实中物种分布存在区本身所形成的空间是非连续的, 因此会出现偏大估计物种分布的现象(Carpenter et al., 1993)。虽然本研究证明通过DOMAIN模型选择不存在数据具有可行性, 但是并不等于分类判别分析模型总是比概形分析模型优越。例如, Hirzel等(2001)发现当物种处于扩散阶段, 还没有完全占据其潜在分布区的时候, 概形分析模型———BIomapper比分类判别分析模型———广义线性模型(generalized linear model, GLM)能更准确地模拟物种分布。Václavík等(2009)也发现利用随机产生虚拟物种不存在数据的分类判别分析模拟(GLM)和概形分析模型(Maxent和Biomapper)的预测精度相似。
影响物种分布的因素众多, 在大陆尺度上气候是主要因素, 随着空间尺度缩小, 地形、土地利用、土壤、生物间相互作用关系逐渐起作用; 此外, 还有物种进化、极端干扰事件等(Pearson et al., 2003; 郭泉水等, 1995; 王娟等, 2009)。由于生态系统的复杂性, 对这些生物过程和极端干扰事件的预测是极其困难的。现实条件下, 物种分布区迁移滞后于气候变化; 但是, 如果气候如所预测的那样变化, 毛竹分布也会朝着预测的方向发展。
郭泉水, 徐德应. 1995. 气候变化对油松地理分布影响的研究[J]. 林业科学, 31(5): 393-402. |
王娟, 倪健. 2009. 中国北方温带地区5种锦鸡儿植物的分布模拟[J]. 植物生态学报, 33(1): 12-24. |
中国科学院中国植被图编辑委员会. 2001. 1:100万中国植被图集[M]. 北京: 科学出版社.
|
周国模. 2006. 毛竹林生态系统中碳储量、固定及其分配与分布的研究. 浙江大学博士学位论文.
|
Allouche O, Tsoar A, Kadmon R. 2006. Assessing the accuracy of species distribution models: prevalence, kappa and the true skill statistic (TSS)[J]. Journal of Applied Ecology, 43(6): 1223-1232. DOI:10.1111/jpe.2006.43.issue-6 |
Araújo M B, New M. 2007. Ensemble forecasting of species distributions[J]. Trends in Ecology and Evolution, 22(1): 42-47. DOI:10.1016/j.tree.2006.09.010 |
Barry S, Elith J. 2006. Error and uncertainty in habitat models[J]. Journal of Applied Ecology, 43(3): 413-423. DOI:10.1111/jpe.2006.43.issue-3 |
Carpenter G, Gillison A, Winter J. 1993. DOMAIN: a flexible modelling procedure for mapping potential distributions of plants and animals[J]. Biodiversity and Conservation, 2(6): 667-680. DOI:10.1007/BF00051966 |
Chefaoui R M, Lobo J M. 2008. Assessing the effects of pseudo-absences on predictive distribution model performance[J]. Ecological Modeling, 210(4): 478-486. DOI:10.1016/j.ecolmodel.2007.08.010 |
Cohen J. 1960. A coefficient of agreement for nominal scales[J]. Educational and Psychological Measurement, 20(1): 37-46. DOI:10.1177/001316446002000104 |
Daly C, Gibson W, Taylor G, et al. 2002. A knowledge-based approach to the statistical mapping of climate[J]. Climate Research, 22(2): 99-113. |
Elith J, Graham C H, Anderson R P, et al. 2006. Novel methods improve prediction of species’ distributions from occurrence data[J]. Ecography, 29(2): 129-151. DOI:10.1111/j.2006.0906-7590.04596.x |
Fielding A H, Bell J F. 1997. A review of methods for the assessment of prediction errors in conservation presence/absence models[J]. Environmental Conservation, 24(1): 38-49. DOI:10.1017/S0376892997000088 |
Freeman E, Moisen G. 2008. Presence absence: an R package for presence absence analysis[J]. Journal of Statistical Software, 23(11): 1-31. |
Gower J C. 1971. A general coefficient of similarity and some of its properties[J]. Biometrics, 27(4): 857-871. DOI:10.2307/2528823 |
Granitto P, Verdes P, Ceccatto H. 2005. Neural network ensembles: evaluation of aggregation algorithms[J]. Artificial Intelligence, 163(2): 139-162. DOI:10.1016/j.artint.2004.09.006 |
Hirzel A, Helfer V, Metral F. 2001. Assessing habitat-suitability models with a virtual species[J]. Ecological Modelling, 145(2/3): 111-121. |
Hirzel A H, Hausser J, Chessel D, et al. 2002. Ecological-niche factor analysis: how to compute habitat-suitability maps without absence data[J]. Ecology, 83(7): 2027-2036. DOI:10.1890/0012-9658(2002)083[2027:ENFAHT]2.0.CO;2 |
Lehmann A, Overton J M, Leathwick J R. 2002. GRASP: generalized regression analysis and spatial prediction[J]. Ecological Modeling, 157(2/3): 189-207. |
Manel S, Williams H C, Ormerod S J. 2001. Evaluating presenceabsence models in ecology: the need to account for prevalence[J]. Journal of Applied Ecology, 38(5): 921-931. |
Monserud R, Leemans R. 1992. Comparing global vegetation maps with the Kappa statistic[J]. Ecological Modelling, 62(4): 275-293. DOI:10.1016/0304-3800(92)90003-W |
Nix H A. 1986. A biogeographic analysis of Australian Elaphid snakes//Longmore R. Atlas of Elapid Snakes of Australia. Canberra: Australian Government Publishing Service, 4-15.
|
O'hanley J R. 2009. NeuralEnsembles: a neural network based ensemble forecasting program for habitat and bioclimatic suitability analysis[J]. Ecography, 32(1): 89-93. DOI:10.1111/eco.2009.32.issue-1 |
Pearson R G, Dawson T P. 2003. Predicting the impacts of climate change on the distribution of species: are bioclimate envelope models useful[J]. Global Ecology and Biogeography, 12(5): 361-371. DOI:10.1046/j.1466-822X.2003.00042.x |
Phillips S J, Anderson R P, Schapire R E. 2006. Maximum entropy modeling of species geographic distributions[J]. Ecological modeling, 190(3/4): 231-259. |
Rangel T, Diniz-Filho J, Bini L. 2006. Towards an integrated computational tool for spatial analysis in macroecology and biogeography[J]. Global Ecology and Biogeography, 15(4): 321-327. DOI:10.1111/geb.2006.15.issue-4 |
Souza Muoz M, Giovanni R, Siqueira M, et al. 2009. OpenModeller: a generic approach to species potential distribution modelling[J]. GeoInformatica, 1(3): 275-316. |
Stockwell D. 1999. The GARP modelling system: problems and solutions to automated spatial prediction[J]. International Journal of Geographical Information Science, 13(2): 143-158. DOI:10.1080/136588199241391 |
Swets J A. 1988. Measuring the accuracy of diagnostic systems[J]. Science, 240(4857): 1285-1293. DOI:10.1126/science.3287615 |
Thuiller W. 2003. BIOMOD-optimizing predictions of species distributions and projecting potential future shifts under global change[J]. Global Change Biology, 9(10): 1353-1362. DOI:10.1046/j.1365-2486.2003.00666.x |
Václavík T, Meentemeyer R K. 2009. Invasive species distribution modeling (iSDM): are absence data and dispersal constraints needed to predict actual distributions[J]. Ecological Modeling, 220(23): 3248-3258. DOI:10.1016/j.ecolmodel.2009.08.013 |
Vanderwal J, Shoo L P, Graham C, et al. 2009. Selecting pseudoabsence data for presence-only distribution modeling: how far should you stray from what you know[J]. Ecological Modeling, 220(4): 589-594. DOI:10.1016/j.ecolmodel.2008.11.010 |
Walker P, Cocks K. 1991. HABITAT: a procedure for modelling a disjoint environmental envelope for a plant or animal species[J]. Global Ecology and Biogeography Letters, 1(4): 108-118. DOI:10.2307/2997706 |
Wang T, Hamann A, Spittlehouse D, et al. 2006. Development of scalefree climate data for western Canada for use in resource management[J]. International Journal of Climatology, 26(3): 383-397. DOI:10.1002/(ISSN)1097-0088 |
 2011, Vol. 47
2011, Vol. 47


