文章信息
- 张冬有, 冯仲科, 李亦秋, 张丽娟, 董斌
- Zhang Dongyou, Feng Zhongke, Li Yiqiu, Zhang Lijuan, Dong Bin
- 基于C-FIX模型的黑龙江省森林植被净初级生产力遥感估算
- Remote Sensing Estimation of Forest Net Primary Productivity in Heilongjiang Province with C-FIX Model
- 林业科学, 2011, 47(7): 13-19.
- Scientia Silvae Sinicae, 2011, 47(7): 13-19.
-
文章历史
- 收稿日期:2010-04-17
- 修回日期:2010-12-22
-
作者相关文章
2. 北京林业大学 北京 100083;
3. 绵阳师范学院 绵阳 621000;
4. 安徽农业大学 合肥 230036
2. Beijing Forestry University Beijing 100083;
3. Mianyang Normal University Mianyang 621000;
4. Anhui Agricultural University Hefei 230036
对不同陆地生态系统植被净初级生产力(net primary productivity, NPP)模拟研究旨在定量分析不同生态系统生产力的时空变化模式和生产力格局, 正确评价植物群落在自然条件下的生产能力。近年来在“粮食安全”和“全球变暖”这2个重大问题的驱动下, 一系列适用于区域和全球尺度的NPP估算模型相继而出(Cramer et al., 1999)。现有的NPP模型大体分为3类:传统的气候相关统计模型、生态系统过程模型和光能利用率模型。其中光能利用率模型有CASA (Potter et al., 1993), GLO-PEM (Prince et al., 1995), GLO-PEM2 (Goetz et al., 1999), TURC(Ruimy et al., 1994), Diagnostic model (Maisongrande et al., 1995)和C-FIX(Veroustraete et al., 2002)等。C-FIX模型在NPP计算中引入了遥感参数, 计算简化, 省去了大量的试验工作, 并可进行区域性计算, 精度较高, 可以实时实地、大范围直观地反映植被NPP的时空变化, 避免了研究者对研究对象的直接干扰, 可以重复观察。
C-FIX模型设计思想来源于Monteith理论的光能利用率模型, 可以在区域及全球尺度上估算3个基本的碳循环分量, 即总初级生产力(GPP)、净初级生产力(NPP)和净生态系统生产力(NEP), 它利用光合作用过程中植物对太阳辐射能的气候效率、吸收效率和光能转化效率这3个利用效率因子来实现NPP估算。Maisongrande等(1995)对Monteith理论的光能利用率模型进行改进, 即将NPP分为GPP和自呼吸2部分计算, 建立了一个新的NPP遥感模型。Veroustraete等(1996)在GPP估算中又加入了归一化气温依赖因子和归一化CO2施肥效应因子这2个效率因子进一步对光能利用率进行制约, 建立C-FIX模型, 提高了GPP的估算精度(卢玲, 2003)。黑龙江省丰富的森林资源形成的巨大碳库发挥着重要的生态和社会效益, 巨大的森林面积和森林蓄积决定了黑龙江省森林NPP和碳循环在全国森林碳汇作用中的重要地位。本研究以黑龙江省森林资源为研究对象, 利用ETM +、DEM和气象数据等资料, 以C-FIX模型为基础, 估算黑龙江省2000年5—9月的森林植被NPP, 可为定量分析黑龙江省森林生态系统生产力的时空变化模式和生产力格局提供参考。
1 研究区概况黑龙江省(121° 11'—135° 05' E, 43° 26'— 53°33'N)森林覆盖率45. 9%, 森林面积、森林总蓄积和木材产量均居全国前列, 是国家最重要的国有林区和最大的木材生产基地。天然林资源是黑龙江省森林资源的主体, 主要分布在大小兴安岭和长白山及完达山地区。植被类型主要有: 1)北温带落叶针叶林分布在大兴安岭山地北部, 树种以兴安落叶松(Larix gmelinii)为主; 2)中温带针阔叶混交林分布于小兴安岭和东部山地, 主要树种有红松(Pinus koraiensis)、云杉(Picea asperatsa)、蒙古栎(Quercus mongorica)、白桦(Betula platyphylla)、山杨(Populus davidiana)等; 3)中温带半湿润半干旱草甸草原分布于松嫩平原。黑龙江省属中温带到寒温带的大陆性季风气候, 年平均气温-4 ~ 5 ℃。气温由东南向西北逐渐降低, 南北差近10 ℃。全省年降水量400 ~ 650 mm。太阳辐射资源比较丰富, 年太阳辐射总量46亿~ 50亿J·m-2, 其中, 5—9月的太阳辐射总量占全年的54% ~ 60%。全年日照2 300 ~ 2 800 h, 其中生长季日照时数占总量的44% ~ 48%。全省土壤有机质含量高, 宜农土壤占全省土壤总面积的40%, 黑土、黑钙土、草甸土面积占全省耕地总面积的67. 6%, 是世界上有名的三大黑土带之一。
2 数据来源及处理 2.1 数据来源研究基础数据主要包括: 39景ETM +遥感影像, 时相为2000年5—9月; 74个气象站点(包括加格达奇) 2000年5—9月的月均气温数据; 黑龙江省(哈尔滨、佳木斯、漠河、黑河和富裕)、吉林省(长春、延吉)、辽宁省(沈阳、朝阳)和内蒙古(海拉尔、通辽)共11个站点的2000年5—9月的月均太阳总辐射数据; 1: 25万黑龙江省地形图以及数字高程模型(DEM); 黑龙江省土壤类型矢量数据库; 黑龙江省2000年MODIS数据NPP年产品; 黑龙江省2000年土地利用现状图等。
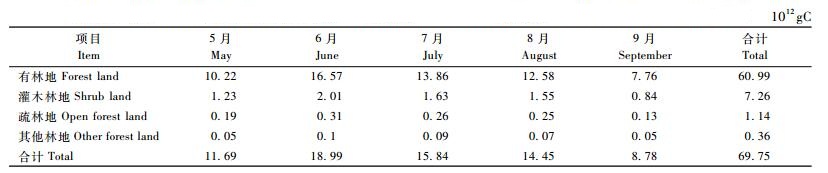
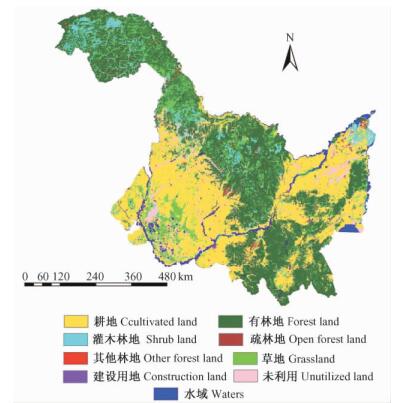
2.2 数据处理 2.2.1 土地利用类型分类黑龙江省2000年遥感影像的土地一级分类共6类:耕地、林地、草地、水域、建设用地和未利用地。由于NPP与林地的关系密切, 为了进一步区分林地, 在土地一级分类的基础上, 将林地再分为4类:有林地、灌木林地、疏林地和其他林地(包括未成林造林地和苗圃等) (图 1)。
|
图 1 土地利用分类 Figure 1 Land-use map |
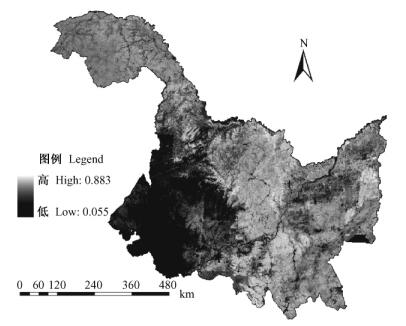
归一化植被指数(NDVI)被定义为近红外波段与可见光红波段数值之差和这2个波段数值之和的比值: NDVI = (ρnir-ρred)/(ρnir + ρred), ρred和ρnir分别为ETM +影像的第3和第4波段反射率。研究区NDVI灰度图见图 2。
|
图 2 NDVI灰度图 Figure 2 Grey image of NDVI |
利用ArcGIS9. 2地学统计分析向导, 采用普通Kriging插值方法, 对74个站点气温进行插值, 插值结果不能覆盖全省。为了插值覆盖全省, 通过建立气温与经纬度的关系模型, 模拟出漠河北、漠河西、宁安南、东宁南和抚远东5个站点5—9月各月气温, 再进行温度插值。
在5—9月的74个站点气温数据中, 选取60个样本参与回归分析, 将气温作为因变量, 将经度和纬度作为自变量, 采用一次趋势面模型(f =b0 + b1x +b2y, f为气温, x为经度, y为纬度, b0, b1和b2为系数)分别建立气温回归模型, 利用未参与回归建模的14个样本分别对各月模型精度进行检验, 预测精度分别达到95. 08%, 96. 51%, 97. 20%, 97. 36%和94. 95%, 预测效果理想。
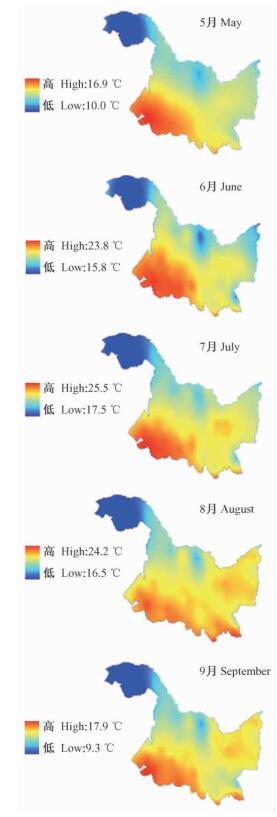
依据建立的气温一次趋势面回归模型, 分别模拟出5个站点5—9月各月气温; 再用全省74个气象站点样本和5个新增模拟温度站点样本, 选用普通Kriging插值得到各月气温插值图(图 3)。
|
图 3 气温插值效果 Figure 3 Effect map of temperature interpolation |
由于黑龙江省只有5个太阳辐射观测站, 分别为哈尔滨、佳木斯、漠河、黑河和富裕, 如果直接利用空间插值方法, 所得太阳辐射预测值必然误差大, 所以补充了长春、延吉、沈阳、朝阳、海拉尔和通辽6个站点2000年5—9月月均太阳总辐射数据。
太阳辐射与经纬度关系密切, 本研究通过建立太阳辐射与经纬度的回归模型, 来模拟黑龙江省各地的辐射值, 进而再利用空间插值方法获取全省连续的太阳总辐射数据。
将太阳辐射作为因变量, 将经度和纬度作为自变量, 采用二次趋势面模型(f = b0 + b1x + b2y +b3x2+ b4xy + b5y2, f为太阳辐射, x为经度, y为纬度, b0, b1, b2, b3, b4和b5为系数)进行回归, 回归方法采用强迫引入法, 分别得到5—9月太阳总辐射回归模型。以5—9月太阳总辐射回归模型为基础, 以已有的黑龙江省74个气温站点和新增5个模拟气温站点的经纬度为自变量, 分别计算出5—9月79个样本的太阳总辐射值, 选用普通克里金、简单克里金和析取克里金3种方法进行内插对比分析, 5月选用简单克里金方法内插效果最好, 其他各月选用普通克里金方法内插效果最好, 得到最优的辐射内插图(图 4)。
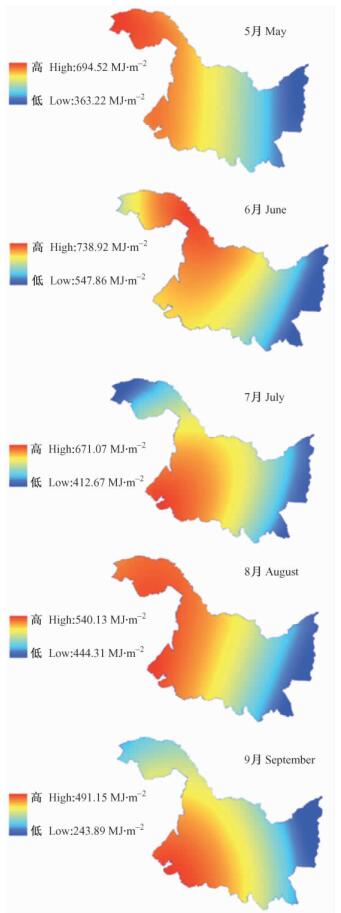
|
图 4 太阳总辐射插值效果 Figure 4 Effect map of global solar radiation interpolation |
采用全国25 m分辨率的DEM作为原始资料, 利用黑龙江省的边界进行裁剪, 同时利用黑龙江省1: 25万的地形图对裁剪后的DEM进行精校正, 得到研究区DEM影像图(图 5)。
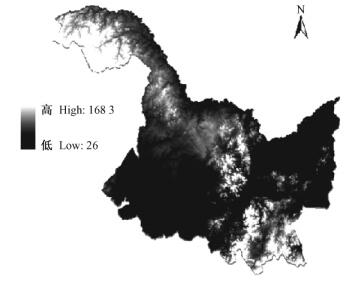
|
图 5 DEM影像 Figure 5 DEM image graph |
本研究NDVI与影像分类数据均采用等面积割圆锥投影, 标准纬度为25°和47°, 中央经线为105°, 空间分辨率定为100 m × 100 m。气温分布图、太阳总辐射图、DEM等所有数据均经投影转换、坐标系定义、重采样和掩膜处理, 将数据的坐标系统、空间分辨率和空间范围统一为与NDVI数据同一标准。
3 C-FIX模型算法及参数修订对于每一给定的点位置或格网, Veroustraete的C-FIX模型分别使用以下公式来计算每天的GPP, NPP和NEP(gC·m-2 d-1) :
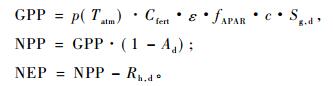
|
式中: p(Tatm)为归一化气温依赖因子, 取值[0, 1]; Cfert为归一化CO2施肥效应因子; fAPAR为植被冠层可吸收的光合有效辐射比例(系数), 取值[0, 1]; ε为光能利用率gC·MJ-1; c为气候效率系数; Sg, d为逐日太阳入射总辐射通量(MJ·m-2 d-1); Ad为植被自养呼吸率; Rh, d为土壤异养呼吸通量(gC·m-2 d-1)。
3.1 归一化气温依赖因子p(Tatm)的计算归一化气温依赖因子p(Tatm)的作用是作为一个消耗系数来反映低温和高温时光合作用内在生化作用对GPP光合作用效率的制约程度, 取值在0和1之间。该因子首先由Wang(1996)提出, 并给出了计算公式:
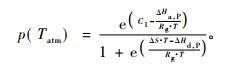
|
式中: C1为常数; T为绝对温度K, ΔS为CO2变性平衡的熵(J·K-1 mol-1); ΔHa, p为活化能, 取值52 750 J·mol-1; ΔHd, p为去活化能, 取值211 000 J·mol-1; Rg为气体常数, 取值8. 31 J·K-1 mol-1。Maselli等(2006)和Chirici等(2007)在使用C-FIX模型估算意大利森林GPP和NPP时, 将C1和ΔS取值与高程结合起来, 山地C1 = 21. 9, ΔS = 710 J·K-1 mol-1; 平原或丘陵C1 = 21. 6, ΔS = 700 J·K-1 mol-1。本研究在计算NPP时, 根据Maselli等(2006)和Chirici等(2007)的研究, 引入黑龙江省DEM数据, 根据每一像元的高程来确定C1和ΔS的取值。
3.2 归一化CO2施肥效应因子Cfert的计算Cfert计算公式如下(Collatz et al., 1991) :
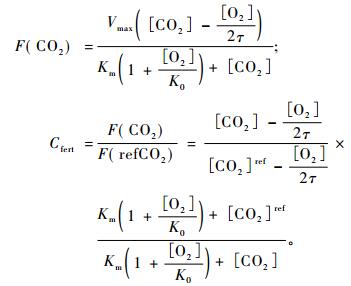
|
式中: F(CO2)和F(refCO2)分别为目前和基准大气CO2浓度下的CO2同化率; τ为CO2和O2浓度比值, 其计算公式为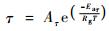
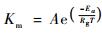
fAPAR为植被冠层吸收的光合作用有效辐射比例, 是光能利用率模型估算NPP的一个关键性中间变量, 其作用是用来推算光合有效辐射, 一般采用遥感植被指数法推算。Myneni等(1994)给出fAPAR = 1.163 8 × NDVI-0.142 6, 建立在物理机制十分明确的三维辐射传输模型和大量的实测数据基础上, 具有普适性且不受像元异质性影响, 相关系数r2 = 0.919。本研究使用的NDVI数据源于黑龙江省2000年5—9月ETM +影像。
3.4 光能利用率ε的确定ε表示植被冠层通过光合作用将吸收的光合作用有效辐射和CO2转化为干物质或有机碳的效率。将归一化气温依赖因子p(Tatm)和归一化CO2施肥效应因子Cfert作为消耗系数对ε进行纠正, 以反映光、热和水3个最重要的气候因子对ε的制约程度。本研究通过对朱文泉(2005)所计算各植被类型结果取平均值来确定模型中的最大光能利用率εmax, 即模型中的最大光能利用率εmax取为0. 49。
3.5 气候效率因子c的确定大量研究表明全球范围内的c值都很稳定且区域变动范围很小, 大多为0. 45 ~ 0. 5。朱志辉等(1985)利用大量气象台站的太阳总辐射(S)资料和莫尔达乌等人(叶菲莫娃, 1983)对光合作用有效辐射的经验计算公式, 推算了我国各省区年总太阳辐射量和光合作用有效辐射分布, 经过面积加权平均, 计算得到黑龙江省c值为0. 49。
3.6 太阳总入射辐射日值Sg, d和气温日值Tatm的计算研究区范围内获得的气象台站观测数据, 只能代表各站点上的太阳辐射值和气温值。本研究基于已有的黑龙江省2000年5—9月的月均温和2000年5—9月太阳总辐射数据, 通过空间Kriging插值方法进行尺度外推(李新等, 2000), 得到研究区研究月份的每月气温插值和太阳总辐射插值图。
3.7 植被自养呼吸率Ad的计算植被自养呼吸率Ad的计算利用Goward等(1987)建立的依赖于温度简单算法: Ad = (7. 825 + 1. 145Ta)/100, Ta为摄氏温度。
4 模型运算结果根据前述对C-FIX模型NPP = p(Tatm)·Cfert·ε· fAPAR·c·Sg, d·(1-Ad)的分析, 使用ERDAS IMAGINE的空间建模工具Model Maker, 建立如图 6所示模型。
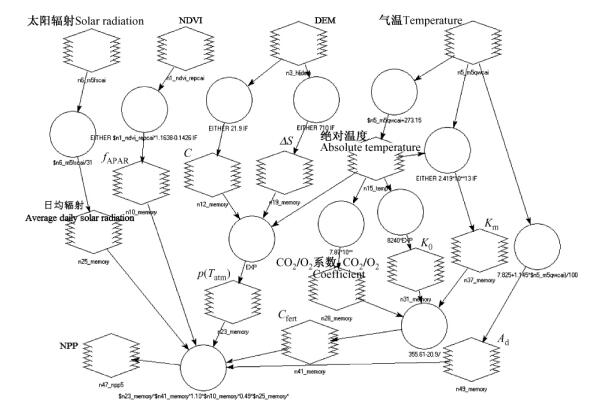
|
图 6 C-FIX图形模型 Figure 6 Graphical model of C-FIX |
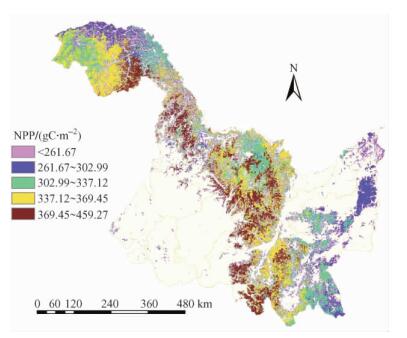
在C-FIX模型中分别输入NDVI数据、DEM数据、各月气温数据、各月太阳辐射数据及其相关参数, 输出各月NPP数据图层, 累加得到黑龙江全省5—9月林地的NPP分布图(图 7), 分别用有林地、灌木林地、疏林地、其他林地掩膜各月NPP数据图层, 得到不同林地类型各月的NPP掩膜图。经统计得到5—9月林地二级分类NPP统计表(表 1)。由表 1可知: 5—9月林地的总NPP为69. 75 × 1012 gC, 其中6月NPP总量最大(18. 99 × 1012 gC), 占5—9月林地NPP总量的27. 23%; 7月份次之(15. 84 × 1012 gC), 5, 8和9月份分别为11. 69 × 1012, 14. 45 × 1012和8. 78 × 1012 gC。6—8月是NPP的主要积累月份。从不同林地类型的NPP累加值来看, 有林地为60. 99 × 1012 gC, 占林地总量的87. 44%;灌木林地为7. 26 × 1012 gC, 占林地总量的10. 41%;疏林地为1. 14 × 1012 gC, 占林地总量的1. 63%;其他林地为0. 36 × 1012 gC, 占林地总量的0. 56%。
|
图 7 5—9月林地NPP分布 Figure 7 Forest NPP distribution map from May to September |
|
|
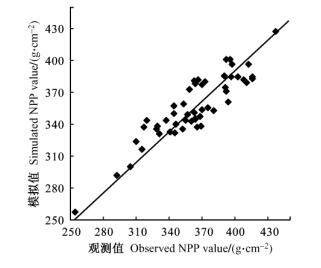
将C-FIX模型计算结果与MODIS的NPP产品MOD17A2对比分析, 以验证模型估算的可靠性。MOD17A2是关于植被初级生产力的产品。本研究利用黑龙江省2000年5—9月NPP产品, 在模型模拟图和MOD17A2产品图的林地中分别随机抽取50个样本点, 将其作为5—9月NPP产品观测值。观测值与模拟值的比较如图 8所示。NPP观测值与模型模拟值之间的均方差根RMSE为17. 12, 模型模拟值误差为观测值的3. 92% ~ 5. 85%, 模型拟合度较高。
|
图 8 NPP模拟值与观测值的比较 Figure 8 Comparison of simulated and observed NPP value |
5—9月林地总NPP为69. 75 × 1012 gC, 其中6月的NPP总量最大, 占5—9月林地NPP总量的27. 23%, 6—8月是NPP的主要积累月份。从不同林地类型的NPP累加值来看, 有林地占林地总量的87. 44%;灌木林地占10. 41%;疏林地占1. 63%;其他林地占0. 56%。
黑龙江省5—9月MODIS NPP产品与5—9月C-FIX模型模拟值具有较好的拟合度, NPP产品值与模型模拟值之间的均方差根为17. 12, 模型模拟值误差为产品值的3. 92% ~ 5. 85%, 可见, 本研究所用的C-FIX模型及其参数选择适合于估算黑龙江省森林生长季的NPP。
遥感模型能实时在大尺度上估算植被NPP, 但复杂的生态系统过程、数据观测或采样的人为干扰、不同的参数选择和算法设计, 以及不同来源不同时空分辨率的数据都会影响NPP估算精度, 今后应加强对各种NPP模型不同尺度估算精度的研究。
李新, 程国栋, 卢玲. 2000. 空间内插方法比较[J]. 地球科学进展, 15(3): 260-265. |
卢玲. 2003. 中国西部地区净初级生产力及碳循环研究. 中国科学院博士学位论文.
|
叶菲莫娃. 1983. 植被产量的辐射因子. 王炳宗, 译. 北京: 气象出版社, 157-202.
|
朱志辉, 张福春. 1985. 我国陆地生态系统的植物太阳能利用率[J]. 生态学报, 5(4): 343-356. |
朱文泉. 2005. 中国陆地生态系统植被净初级生产力遥感估算及其与气候变化关系的研究. 北京师范大学博士学位论文.
|
Collatz G J, Ball J T, Grivet C, et al. 1991. Physiological and environmental regulation of stomatal conductance, photosynthesis and transpiration: a model that includes a laminar boundary layer[J]. Agricultural and Forest Meteorology, 54(3/4): 107-136. |
Cramer W, Kicklighter D W, Bondeau A, et al. 1999. Comparing global models of terrestrial net primary productivity (NPP): overview and key results[J]. Global Change Biology, 5(Supp.1): 1-15. |
Chirici G, Barbati A, Maselli F. 2007. Modelling of Italian forest net primary productivity by the integration of remotely sensed and GIS data[J]. Forest Ecology and Management, 246(2/3): 285-295. |
Goward S N, Dye D G. 1987. Evaluating North-American net primary productivity with satellite observation[J]. Advanced in Space Research, 7(11): 165-174. DOI:10.1016/0273-1177(87)90308-5 |
Goetz S J, Prince S D, Goward S N, et al. 1999. Satellite remote sensing of primary production: an improved production efficiency modeling approach[J]. Ecological Modelling, 122(3): 239-255. DOI:10.1016/S0304-3800(99)00140-4 |
Maisongrande P, Tuimy A, Dedieu G, et al. 1995. Monitoring seasonal and interannual variation of grass primary productivity, net primary productivity and ecosystem productivity using a diagnostic model and remotely sensed data[J]. Tellus, 47(8): 178-190. |
Maselli F, Barbati A, Chiesi M, et al. 2006. Use of remotely sensed and ancillary data for estimating forest gross primary productivity in Italy[J]. Remote Sensing of Environment, 100(4): 563-575. DOI:10.1016/j.rse.2005.11.010 |
Myneni R B, Williams D L. 1994. On the relationship between fAPAR and NDVI[J]. Remote Sensing of Environment, 49(3): 200-211. DOI:10.1016/0034-4257(94)90016-7 |
Potter C S, Randerson J, Field C B, et al. 1993. Terrestrial ecosystem production: a process model based on global satellite and surface data[J]. Global Biogeochemical Cycle, 7: 811-841. DOI:10.1029/93GB02725 |
Prince S D, Goward S N. 1995. Global primary production: a remote sensing approach[J]. Journal of Biogeography, 22(4/5): 815-835. DOI:10.2307/2845983 |
Ruimy A, Saugier B, Dedieu G. 1994. Methodology for the estimation of terrestrial net primary production from remotely sensed data[J]. Journal of Geographical Research, 99(3): 5263-5283. |
Veroustraete F, Sabbe H, Eerman E. 2002. Estimation of carbon mass fluxes over Europe using the C-FIX model and Euroflux data[J]. Remote Sensing of Environment, 83(3): 376-399. DOI:10.1016/S0034-4257(02)00043-3 |
Veroustraete F, Patyn J, Myneni R B. 1996. Estimating net ecosystem exchange of carbon using the normalized difference vegetation index and an ecosystem model[J]. Remote Sensing of Environment, 58(1): 115-130. DOI:10.1016/0034-4257(95)00258-8 |
Wang K Y. 1996. Canopy CO2 exchange of Scots pine and its seasonal variation after four year exposure to elevated CO2 and temperature[J]. Agricultural and Forest Meteorology, 82(1/4): 1-27. |
 2011, Vol. 47
2011, Vol. 47