文章信息
- 巨云为, 李明阳, 吴文浩
- Ju Yunwei, Li Mingyang, Wu Wenhao
- 江苏省松材线虫发生的预测方法
- Predictive Methods of Pine Wilt Disease in Jiangsu Province
- 林业科学, 2010, 46(12): 91-96.
- Scientia Silvae Sinicae, 2010, 46(12): 91-96.
-
文章历史
- 收稿日期:2009-08-13
- 修回日期:2010-01-04
-
作者相关文章
2. 江苏省有害生物入侵预防与控制重点实验室 南京 210037
2. Jiangsu Key Laboratory for Prevention and Management of Invasive Species Nanjing 210037
松材线虫(Bursaphelenchus xylophilus)是松材线虫病的主要病原生物。松材线虫病对世界林业经济造成了极为严重的损失,已有40多个国家将其列为检疫对象(柴希民等,2003)。目前世界上松材线虫病的分布地区包括美国、加拿大、墨西哥、中国、韩国、日本和葡萄牙等。在日本、韩国和中国,松材线虫病引起松树(Pinus)大量死亡。我国于1982年在南京紫金山首次发现松材线虫,根据《中国绿色时报》 2009年8月21日报道,2008年全国松材线虫病发生面积6.428万hm2,病死松树106.17万株,2009年已扩散到皖、浙、粤、赣、鄂等15个省(市)的193个县(区),目前,还在持续扩散。
江苏地处长江下游,属平原农区省份,松树是江苏省丘陵山区和风景名胜区的主要造林绿化树种,全省共有松林面积93 333 hm2,其中易感病树种马尾松(Pinus massoniana)林46 667 hm2,黑松(P.thunbergii)林和赤松(P.densiflora)林面积3.8万hm2,集中分布在宁镇、宜溧山区、环太湖沿岸风景区和沿海云台山区。由于经济活跃,对外贸易频繁,温湿条件适宜,森林破碎化严重,松材线虫病危害现象十分严重。自1982年以来,已累计死亡松树500万株以上,损失木材25万m3,直接经济损失超过2亿元,严重影响了疫区当地经济和社会的可持续发展(解春霞等,2002)。
防止外来生物入侵造成危害的重要手段是阻止可能造成入侵的物种进入适合其生存的地区,即探明物种一旦进入将会在什么地方生存,其生存、暴发的可能性以及扩散的范围有多大。金昊(1993)、魏初奖(1997)、冯士明(2000)和吕全等(2005)从不同侧面和程度进行了松材线虫的潜在生境适生分析,但与致病机制、发生现状及防治措施研究相比,这些研究比较薄弱,主要体现在: 1)一般多局限于单一模型的研究,缺乏多种生态位模型的预测性能比较; 2)在外来森林病虫害潜在生境主要生态环境因子的选择上,主观因素较多,缺乏适生概率与生态环境因子关系的量化分析; 3)研究的尺度较大,预测的结果比较粗糙,并且与松材线虫跳跃式离散分布的空间分布格局不相一致; 4)在潜在生境分析基础上,缺乏松材线虫病发生及面积预测的进一步研究。
本文以2007年松材线虫在江苏发生的75个地面定位调查数据、国内外开放式基础地理信息和生态环境数据库的68个环境因子为主要信息源,分别采用分类与回归树(CART)、基于规则的遗传算法(GARP)、最大熵法(Maxent)、逻辑斯蒂回归(LR)4种生态位模型,建立潜在生境预测模型,通过接受者运行特征曲线下面积(AUC)、Pearson相关系数COR、Kappa值3个指标来检验预测模型精度,在此基础上进行松材线虫的空间分布规律及其环境影响因子分析,并预测各县(区)发生概率和发生面积,以期探索出一条经济适用的松材线虫病早期预警研究方法。
1 材料与方法 1.1 数据源2007年10月至2008年1月,在江苏省连云港市云台区和新浦区、南京市3个松材线虫病发生县(区),根据当地林业部门提供的松材线虫发生地小地名资料,采用现场观测、手持GPS定位的方式,提取出80个发生地经纬度坐标,删除重复或距离太近的坐标点,实际提取松材线虫发生点75个。
从国家基础地理数据库(http://nfgis.nsdi.gov.cn/)下载的1: 400万中国矢量地图中提取江苏省行政区划图作为分析底图。从世界气象数据库(http://www.worldclim.org/)通过掩模运算提取江苏省55个气候因子,包括年降水量、降水季节性变化、1—12月份各月最高温度、1—12月份各月最低温度、1—12月份各月降水量; 根据McCune等(2002)的研究成果,计算得到江苏省太阳辐射数据; 通过江苏省数字地形模型(DEM)得到海拔、坡度、东西坡向、南北坡向、水流方向、复合地形指数等7个地形、水文因子; 从全球土地覆盖基础数据库(GLCF)(http://www.landcover.org/)提取江苏省林木覆盖率、增强型植被指数; 从美国地质调查局(USGS)的亚洲1 000 m像素分辨率的水文数据库(http://edc.usgs.gov/products/elevation/gtopo30/hydro/asia.html)提取江苏省土壤类型、土壤pH值和土壤湿度3个土壤因子。合计提取气候、地形、土壤、水文、植被等各种生态环境因子68个。
1.2 建模方法 1.2.1 决策分类树模型由于不需要对相关的变量进行预先筛选,数据的变换对预测结果不产生影响,CART经常被研究者用来分析多元数据(Feldesman,2002)。CART模型的优点在于它可以兼容连续和分类2种变量,具有处理遗失数据的能力,能够捕捉变量之间复杂的层次和非线性关系(Clark et al., 1993)。Kelly等(2002)采用CART模型,在景观尺度上揭示了美国加利福尼亚州一个公园里影响橡树猝死病发生和发展的主要生态环境因子。
1.2.2 基于规则的遗传算法GARP模型采用一种称为遗传算法的人工智能运算框架(Stockwell et al.,1999)。该模型能够通过产生一套正面、负面规则,来进行二进制预测。正面的规则可以预测满足某些环境条件的某一物种的适合生境,而负面规则可预测不满足环境条件的不适合生境。遗传算法的用途在于通过启发的方式,解决多种预测结果之间的冲突(Stockwell et al., 1992)。
1.2.3 最大熵法Maxent模型的基本思想是为所有已知的因素建立模型,而把所有未知的因素排除在外(Phillips et al., 2006)。Maxent模型的一个最显著的特点是其不要求变量之间相互独立,因此人们可以相对任意地加入对最终分类有用的环境变量,而不用考虑它们之间的相互影响。该模型的优点使其成功地应用于图像重建、投资组合优化、统计物理学、信号处理和生态位空间建模领域。当Maxent模型应用于物种潜在生境建模时,研究区域的栅格图像所覆盖的空间范围构成了Maxent概率分布定义的总体,全球定位系统(GPS)定点发生数据集合构成了总体的一个抽样样本,而每个发生点(样本单元)的环境因子,如气候变量、海拔、土壤类型和太阳辐射构成了样本单元特征。
1.2.4 逻辑斯蒂回归LR是生物多样性潜在生境空间建模最常用的一种生态位模型,它是传统多元线性回归模型的一种变形(Franklin,1995)。区别在于,LR模型的因变量是1和0组成的二进制变量,分别代表某些事件发生和不发生2种状态,自变量可以是连续变量,也可以是分类变量。模型预测的结果可以在GIS平台上,以通俗易懂的概率空间分布图的形式显示出来。Kelly等(2001)根据测深雷达数据,采用LR模型来进行美国海洋外来入侵植物的潜在生境空间分布制图。为了制定森林管理策略,Felicisimo等(2002)根据地形、受海洋影响大小等生态环境因子,采用LR模型对西班牙北部6种森林类型的潜在生境进行预测。
1.3 数据处理数据处理工具主要有:美国ESRI公司开发的地理信息系统平台ArcGis 9.2、美国堪萨斯大学生物多样性研究中心开发的Desktop Garp1.1.6、美国普林斯顿大学AT & T实验室Philips等开发的Maxent 3.1.0、德国波茨坦大学地生态学研究所Bonn等开发的ROC-Plot以及由美国SYSTAT软件公司开发的统计分析软件SYSTAT 12.0。
松材线虫潜在生境生态因子的提取通过ArcGis9.2平台上外挂式分析工具HawthTools来实现。GARP模型的建立通过Desktop Garp 1.1.6软件实现,Maxent模型的建立通过Maxent 3.1.0软件实现,相关系数COR运算、LR模型、CART模型的建立通过SYSTAT 12.0软件实现。预测模型验证指标AUC及P-Kappa的计算通过ROC-Plot程序实现。
1.3.1 主要生态环境因子的提取选择坡度、海拔、降水季节性变化、太阳辐射等68个因子作为分析松材线虫潜在生境的生态环境因子。在68个因子中,许多变量之间存在着较强的相关性,这种相关性会增大主要生态环境因子的识别难度,另外无法满足LR模型独立、正态的要求。为此在对75个松材线虫江苏发生点68个生态环境因子进行Pearson相关分析基础上,运行Maxent模型,计算出各个环境变量对预测概率的贡献值。在相互关联的多个变量中,选取对预测概率贡献最大的变量作为建模变量。共筛选出坡度(slope,58.0%)、降水季节性变化(bio15,12.9%)、复合地形指数(CTI,8.2%)、最干燥季节平均温度(bio9,7.8%)、南北坡向(northness,2.8%)和最温暖月份最高温度(bio5,1.6%)6个环境变量,累计贡献率达91.3%,以此6个变量作为松材线虫潜在生境预测建模的主要环境因子。
1.3.2 松材线虫未发生点的生成在4个潜在生境预测模型中,GARP和Maxent模型只要求提供发生点(presence point)空间数据,但LR和CART模型的建立同时需要具备松材线虫未发生点和已发生点的地理坐标数据,同时这4个生态位预测模型的验证也需要同时具备已发生点和未发生点坐标数据。在外来入侵物种生境建模中,通常将发生点以外的背景作为未发生地。在ArcGis软件中,以配准好的江苏省行政界线图为空间参考,随机生成2 000个抽样点。通过ArcGis平台上外挂式分析工具HawthTools中的Intersect Point Tool提取这些点的Maxent预测概率,根据统计学原理,将发生概率小于0.05的抽样点作为未发生点,共生成1 816个未发生点。通过ArcGis中的Merge运算,将松材线虫在江苏的已发生地和未发生地的地理坐标点合并,生成统一的生态位建模空间数据库,将发生点的概率设置为1,未发生点的概率设置为0。在空间数据库中,70%(1 324)的样本点用来建模,其余30%(567)的样本点用来模型验证。
1.3.3 松材线虫病发生面积预测选择综合评价性能最优的生态位模型,根据统计学概率论原理,将发生概率> 0.95的像素点作为松材线虫发生点,设置像素值为1,小于0.95的像素点值为0。在ArcGis平台上,加载江苏省林木覆盖率栅格图层,根据我国森林规划设计调查技术规范,设置阈值0.2,将林木覆盖率(郁闭度)≥0.2的像素点作为森林,并赋值1,小于0.2赋值0。在Raster Calculator工具支持下,通过逻辑“与”运算,提取地类为森林且发生松材线虫概率> 0.95的像素点作为松材线虫病预测发生点。在生成松材线虫病预测发生栅格图层基础上,加载江苏省行政区划矢量图层,进行Zonal Statistic运算,计算出江苏省各县(区)松材线虫病平均发生概率和发生面积。
2 结果与分析 2.1 预测模型的建立选取与松材线虫潜在生境密切相关的6个环境变量,分别带入相应的模型中,进行潜在生境预测。
对于CART模型,在SYSTAT 12.0软件的Trees(CART)模块中,分别输入6个变量,得到的决策树中只有坡度(slope)、最干燥季节平均温度(bio9)和降水季节性变化(bio15)3个环境变量起作用。在生成的CART模型的基础上,借助于ArcGis平台的Raster Calculator中的条件判断函数con(),通过公式(1)进行参数反演,生成松材线虫在江苏的潜在生境预测概率图(图 1)。CART模型的PRE(proportional reduction in error)为0.905,即预测模型能够解释90.5%的环境变量差异,模型拟合精度较高。
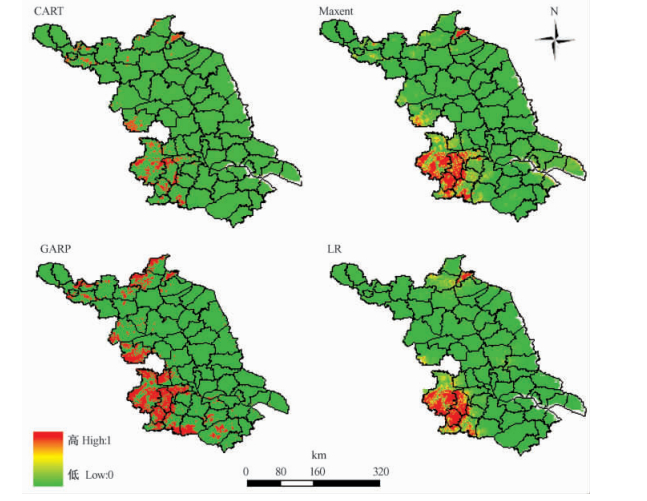
|
图 1 松材线虫在江苏省潜在生境分布 Figure 1 Potential habitat map for pine wood nematode in Jiangsu Province |
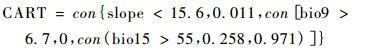
|
(1) |
对于Maxent模型,第1次运算的目的在于识别影响松材线虫发生的主要环境变量,同时辅助生成松材线虫未发生点数据。模型在第2次运算时,仅带入第1次运算筛选出的6个主要环境变量,得到松材线虫在江苏的潜在生境预测概率图。模型的AUC为0.982,说明模型的拟合精度很高(图 1)。
对于GARP模型,由于模型本身运行的不稳定性,每次运算结果都不相同(Stockwell et al., 1999)。因此采用Desktop Garp软件缺省配置(20次运算,每次最大迭代数为1 000,收敛值0.01),模型输出的结果选择为最佳子集。在运行结果产生的最佳子集中,选择训练精度最高(0.900 4)的运算结果所对应的概率分布图作为该模型的预测概率图(图 1)。
对于LR模型来说,所有变量都必须满足正态、独立的条件,所以必须对不符合正态分布的坡度(slope)、降水季节性变化(Bio15)和最温暖月份最高温度(bio5)3个环境变量分别进行常用对数、正弦变化,以满足LR建模要求。LR模型如下:
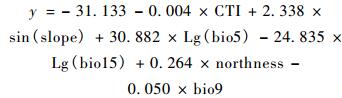
|
(2) |
式中: CTI为地形湿度指数; sin和Lg分别为数据的正弦和常用对数变换。LR模型的Naglekerke's R2为0.856,即预测模型能够解释85.6%的环境变量差异,模型拟合精度较高。在此基础上,利用ArcGis中的Raster Calcu-lator,通过公式LR=Exp(y)/[Exp(y)+1]进行参数反演,得到松材线虫潜在生境概率预测图(图 1)。
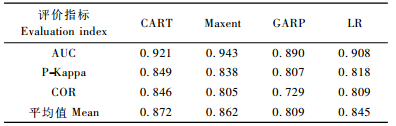
2.2 模型验证分别采用AUC,P-Kappa和COR这3个统计指标来评价预测模型的性能。AUC是ROC曲线常用的评价指标,是一个与参考阈值无关的统计量,它通过百分比的方法计算解靴带置信区间(bootstrapconfidence interval),来评价模型存在点和背景点的诊断性能(Hanly et al., 1982)。AUC的理论取值范围为0.5~1,一般认为AUC值在0.5~0.7时模型诊断价值较低; 在0.7~0.9时诊断价值中等; 大于0.9时诊断价值优秀。Kappa统计量与判断阈值紧密相关,具有机会改正的能力,综合考虑了冗余和代表误差的影响(Cohen,1960)。Kappa统计量取值范围为[-1,1],值越靠近1表明模型预测的效果越理想,等于或小于0时表明模型的预测效果不如随机分布模型效果好。采用最大Kappa值P-Kappa来衡量模型的精度。COR也称为点双列相关系数,一般通过Pearson相关系数计算得来,与基于等级的AUC不同,COR考察的重点是验证数据观测值和模型预测值的偏离程度(Zheng et al., 2000)。
从表 1可以看出,4个模型的AUC值均大于0.8,说明选择的预测模型诊断价值都达到了中等或优秀水平。按照总体平均值从高到低的顺序排序,4个模型的诊断价值依次为: CART(0.872)>Maxent(0.862)> LR(0.845)> GARP(0.809)。在4个模型中,CART模型在P-Kappa,COR和平均值3个方面得分最高。因而,采用CART模型结果来进行松材线虫病发生面积预测。
|
|
从图 1可以看出,松材线虫的潜在生境集中分布在宁镇、宜溧山区、环太湖沿岸风景区和沿海云台山区,与江苏松树的集中分布区域相吻合。结合CART模型与LR模型,分析松材线虫的潜在生境适生概率与6个生态环境因子的量化关系。
从2.1中的CART模型可以看出,松材线虫适宜在坡度较高的丘陵和山区(slope > 15.6°)、最干燥季节平均温度较低(bio9 < 6.7 ℃)、降水季节性变化较小(bio15 < 55%)的环境生存。从2.1中的LR回归方程可以看出,松材线虫的潜在生境适生概率与复合地形指数(CTI)呈负相关,与最温暖月份最高温度(bio5)呈正相关,南坡潜在生境适生概率明显高于北坡。在江苏省,最干燥的季节为夏季,而最温暖的季节为春季。LR模型表明,在生境选择上,松材线虫虽然喜欢温暖潮湿的春季,却难耐炎热干旱夏季的高温。
CTI也称为地形湿度指数,是坡度和像素单元垂直于水流方向的积水区面积的函数。Moore等(1993)研究表明,CTI与土壤深度(r=0.55)、有机质含量(r=0.57)和磷含量(r=0.53)正相关,是表征土壤肥力的一个环境变量。一般情况下,CTI越高,土壤越肥沃; CTI越低,土壤越贫瘠。
上述生态环境因子分析表明,在气候选择上,松材线虫适宜在年均温度较高、降水季节性变化较小的暖温带、亚热带地区生存; 在立地条件选择上,趋向于土壤比较贫瘠的丘陵山区阳坡。
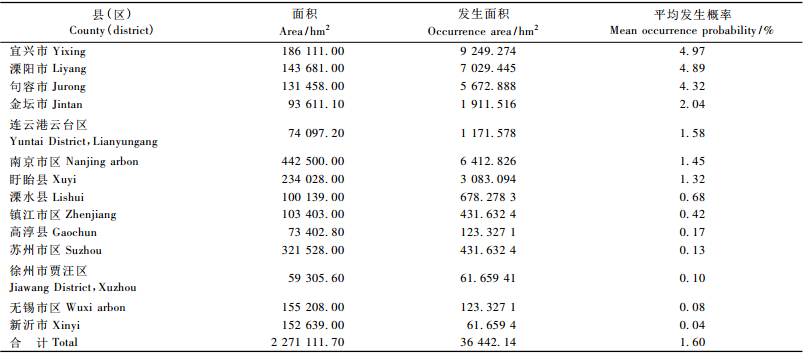
2.4 发生概率及面积计算从表 2可以看出,按照发生概率从大到小排列,江苏省容易感染松材线虫病的区域(前5名)依次为宜兴市、溧阳市、句容市、金坛市和连云港云台区。按照发生面积从大到小排列,松材线虫病在江苏的主要分布区(前5名)依次为宜兴市、溧阳市、南京市区、句容市和盱眙县。松材线虫病预测发生面积为36 442.14 hm2,占江苏省松林面积(93 333 hm2)的39.04%,是已发生面积(13 333 hm2)的2.73倍。
|
|
1) 气候、地形、土壤是影响松材线虫空间分布的主要环境因子。其中,坡度、复合地形指数、坡向与松材线虫寄主—松林的空间分布有关,而最干燥季节平均温度、降水季节性变化、最温暖月份最高温度则是影响松材线虫传媒昆虫—松墨天牛(Monochamus alternatus)的主要环境因子。因此,研究松材线虫的潜在生境,必须综合考虑寄主植物和传媒昆虫的生态环境因子。
2) Graham(1992)在研究大量化石生物的基础上,认为物种的生境更多地与温度和降水的极值而不是和平均值有关。本研究结果印证了其研究结论。值得注意的是,本研究是建立在研究地区特定的自然环境条件基础之上的,研究结论是否适用于其他地区,尚需谨慎对待。
3) 在所取的6个生境因子中,气候因子难以改变,但可适地适树,能提高松林造林质量和改变林分组成,还可改善林地土壤状况,提高林木抗病能力,这些措施都将是松材线虫防治策略的主要组成部分。根据分析,江苏省松材线虫病预测发生面积占江苏省松林面积的39.04%,是已发生面积的2.73倍,因此防治松材线虫发生和大面积扩散是该省一项长期而艰巨的任务。
目前我国现有的外来森林病虫害基础研究资料不全,数据难以实现共享,借助于开放式Web基础地理信息和生态环境数据库,在病原微生物生态位建模的基础上,进行外来森林病虫害发生面积预测,对我国主要外来森林病虫害的预警研究具有借鉴作用。
柴希民, 蒋平. 2003. 松材线虫病的发生与防治[M]. 北京: 中国农业出版社.
|
冯士明. 2000. 松材线虫在云南发生的可能性及预防对策[J]. 植物检疫, 14(5): 289-290. |
金昊. 1993. 从适生性分析松材线虫对云南松树树种的威胁[J]. 云南林业科技, (2): 58-60. |
吕全, 王卫东, 梁军, 等. 2005. 松材线虫在我国的潜在适生性评价[J]. 林业科学研究, 18(4): 460-464. |
魏初奖. 1997. 松材线虫病在福建省的潜在危险性分析及检疫对策[J]. 福建林业科技, 24(1): 54-57. |
解春霞, 郑华英, 张培. 2002. 试论江苏省松材线虫病发生与防治对策[J]. 江苏林业科技, 29(3): 41-43. |
杨宝君, 贺长洋, 王长法. 1999. 国外松材线虫病发生概括[J]. 森林病虫通讯, (5): 40-42. |
Cohen J A. 1960. Coefficient of agreement for nominal scales[J]. Educational and Psychological Measurement, 20: 37-46. DOI:10.1177/001316446002000104 |
Feldesman M R. 2002. Classification trees as an alternative to linear discriminant analysis[J]. American Journal of Physical Anthropology, 119: 257-275. DOI:10.1002/(ISSN)1096-8644 |
Felicisimo A M, Frances E, Fernandez J M, et al. 2002. Modeling the potential distribution of forests with a GIS[J]. Photogrammetric Engineering & Remote Sensing, 68(5): 455-462. |
Franklin J. 1995. Predictive vegetation mapping: geographical modeling of biospatial patterns in relation to environmental gradients[J]. Progress in Physical Geography, 19: 474-499. DOI:10.1177/030913339501900403 |
Graham A.1992.The current status of the legume fossil record in the Caribbean region//Herendeen P S, Dilcher D L.Advances in Legume Systematics.London: Royal Botanical Gardens, Kew, 161-167.
|
Hanly J A, McNeil B J. 1982. The meaning and use of the area under a Receiver Operating Characteristic(ROC)curve[J]. Radiology, 143: 29-36. DOI:10.1148/radiology.143.1.7063747 |
Kelly M. 2007. Modeling the risk for a new invasive forest disease in the United States: an evaluation of five environmental niche models[J]. Computers, Environment and Urban Systems, 31(6): 689-710. DOI:10.1016/j.compenvurbsys.2006.10.002 |
Kelly M, Meentemeyer R K. 2002. Landscape dynamics of the spread of Sudden Oak Death[J]. Photogrammetric Engineering & Remote Sensing, 68(10): 1001-1009. |
Kelly N M, Fonseca M, Whitfield P. 2001. Predictive mapping for management and conservation of seagrass beds in North Carolina[J]. Aquatic Conservation: Marine and Freshwater Ecosystems, 11(6): 437-451. DOI:10.1002/(ISSN)1099-0755 |
McCune B, Keon D. 2002. Equations for potential annual direct incident radiation and heat load[J]. Journal of Vegetation Science, 13: 603-606. DOI:10.1111/j.1654-1103.2002.tb02087.x |
Moore I D, Gessler P E, Nielsen G A, et al. 1993. Terrain attributes: estimation methods and scale effects.Modeling Change in Environmental Systems.[M]. London: Wiley: 189-214.
|
Phillips S J, Anderson R P, Schapire R E. 2006. Maximum entropy modeling of species geographic distributions[J]. Ecological Modeling, 190: 231-259. DOI:10.1016/j.ecolmodel.2005.03.026 |
Stockwell D, Peter D. 1999. The GARP modeling system: problems and solutions to automated spatial prediction[J]. International Journal of Geographical Information Science, 13(2): 143-158. DOI:10.1080/136588199241391 |
Stockwell D R B, Noble I R. 1992. Induction of sets of rules from animal distribution data: a robust and informative method of data analysis[J]. Mathematics and Computers in Simulation, 33: 385-390. DOI:10.1016/0378-4754(92)90126-2 |
Venables W N, Ripley B D. 2002. Modern applied statistics with S[M]. 4th ed. New York: Springer: 20-40.
|
Zheng B, Agresti A. 2000. Summarizing the predictive power of a generalized linear model[J]. Statistic in Medicine, 219: 1771-1781. |
 2010, Vol. 46
2010, Vol. 46