文章信息
- 裴铁璠, 金昌杰, 王本楠, 刘家冈
- Pei Tiefan, Jin Changjie, Wang Bennan, Liu Jiagang
- 自相似河网的降雨-径流响应———一种函数递归迭代算法
- Rainfall-Runoff Response in Self-Similar River Networks———a Study of a Recursive Replacement Algorithm of Function
- 林业科学, 2010, 46(12): 36-41.
- Scientia Silvae Sinicae, 2010, 46(12): 36-41.
- DOI: 10.11707/j.1001-7488.20101206
-
文章历史
- 收稿日期:2008-10-16
- 修回日期:2010-11-01
-
作者相关文章
2. 中国科学院系统生态研究中心 北京 100086;
3. 北京林业大学理学院 北京 100083
2. Department of System Ecology, Chinese Academy of Sciences Beijing 100086;
3. School of Science, Beijing Forestry University Beijing 100083
众所周知,河网的主河道往往可分岔为若干支流,而每条支流又可分岔,如此不断分岔,直到不能再分为止,这意味着河网可以用递归方法生成。很早以前,水文学家就认识到河网是统计意义下的自相似系统(Horton,1945; Strahler,1952; Hack's,1957)。自相似代表一个系统在标度变换下的对称性。1977年Mandelbrot提出分形几何理论(Mandelbrot,1977),至今已被广泛应用到物理、化学、生物、生态、地学和地理领域。1983年Mandelbrot又首先提出河流的分形性质(Mandelbrot,1983),并且将分形对象的自相似性引进河网。此后开展了河网分形性质研究,许多河流系统结构的定量几何描述已经完成(La Barbela et al., 1987; 1989; Nikora,1988)。另一方面,植被对小流域径流的影响可以用试验方法研究,但植被对大流域径流的影响还不能用试验方法很好地估算。如何利用测量到的小流域降雨-径流数据去分析大流域径流,这种尺度变换问题是水文学研究中的一个重要课题,。
目前,国内外已经开展了很多关于河流分形几何学性质的研究,笔者认为,当前应该将研究重点转移到分形动力学方面,也就是研究具有分形特征物体的动力学行为。本研究的河流降雨-径流响应就是这样一个分形动力学问题。本研究提出一种函数递归迭代(RRF)算法,可以用最小流域测量到的数据直接计算自相似河网(SSN)的径流函数(显然这是一个水文过程的尺度变换工具,在个人计算机上,RRF算法用一组递归方程很容易从小流域测量的数据去计算大流域的径流),并采用这种函数递归迭代算法及中国东北辽河小流域上测量的降雨-径流2组数据,分析森林对大流域径流的影响。
1 函数递归迭代算法为了便于建模,作如下理想化基本假定: 1)研究对象是确定性的严格自相似河网,它是实际河网的理想模型; 2)流水经过相同的距离需要相同的时间; 3)降雨落入最小流域,然后分配进入蒸发、下渗、截留和径流,只有其径流才是对大流域的输入; 4)除最小流域外,其他所有河道既不考虑蒸发,也不考虑垂直下渗。
Horton-Strahler河流分级系统给予最外枝的阶数为0,而给主河道以最高阶(Horton,1945; Strahler,1952)。考虑到河网系统的分级是一个无限过程,本研究分配给主河道的阶数为0,而给最外枝以最高阶。
形式地采用众所周知的Horton (1945)-Strahler (1952)长度比关系,令长度比RL为2,于是
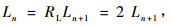
|
(1) |
式中: Ln为第n阶河道的长度,而
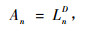
|
(2) |
An和D分别为n阶小流域面积和Hack (1957)为河网引进的分维。令初始联结的长度L0 = 1,因此A0 = 1,考虑到(1)和(2)式,有
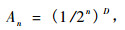
|
(3) |
因为河网的自相似性质,如果在全流域均匀降雨,则相同阶数的河道有相同的结构和相同的径流函数。令Fn(t)表示在n阶流域出口的n阶径流函数,其量纲是L3/T,t表示时间。为方便,定义一个归一化径流函数作为单位面积上的径流函数fn (t),其量纲为L/T:
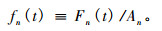
|
(4) |
本研究采用本领域文献Wang等(2002)中常用的严格自相似河网的T1和T2结构。
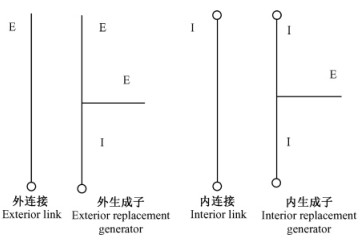
1.1 T1型河流的函数递归迭代算法 1.1.1 T1型河流的递归迭代T1型河流的连接被分类为内连接和外连接。内连接是那些联结2个节点的连接,在上河道和下河道的端点各有1个节点。外连接只有1个节点联结下河道的端点(图 1)。外连接被外生成子替代,后者有2个外连接和1个内连接。内连接被内生成子替代,后者有1个外连接和2个内连接。
|
图 1 T1型河网外连接、外生成子、内连接和内生成子图式 Figure 1 Sketch of the exterior link, the exterior replacement generator, the interior link and the interior replacement generator in T1 river ○:节点Node; E:外连接Exterior link; I:内连接Interior link.下同The same below. |
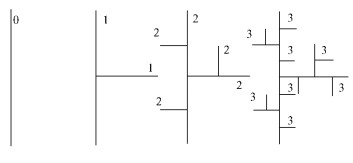
图 2展示了T1型河流从单位长度的初始子开始的递归过程。初始子被生成子所替代,生成子的每一段于是变成一个新的初始子,并再一次地被迭代。在这个递归过程中,内连接用内生成子替换,而外连接用外生成子替换。正如图 2所展示的,生成开始于单个0阶外连接(主河道),并且限定其生成子是1阶的枝杈。在构造的过程中河道长度以固定比例RL不断衰减,同时河道数一步一步增加。这个过程可以认为是大河流不断细化的过程,反之是小河道不断汇聚成大河流的过程。
|
图 2 T1型河网递归迭代生成子图式(0 ~ 3级河道) Figure 2 Sketch of the recursive replacement generation for the T1 river (the rivers of order 0-3) |
本研究提出的函数递归迭代算法(RRF)建立在以下对应法则基础上。
1) 迭代的起点是初始子,它是0阶外连接(图 3)。同时,相应的操作是将0级径流函数F0(t) =f0 (t)放在公式(5)的左边,这个0阶径流函数正是我们想要的。

|
图 3 T1型河网函数递归迭代图示 Figure 3 Schetch of recursive replacement of function for the T1 river networks |
2) 迭代的第1步是初始子被外生成子所替代,后者有2个1阶的叶子(叶子形象地表示流域)(图 3)。对应于这2片叶子,2个1阶径流函数2A1f1(t-τ/2)被放到公式(5)的右边,正如公式(5)第1行所显示的。τ为流水经过主河道的全长(L0 = 1)的流动时间。时间延迟(τ/2)是因为从1阶河道出口到主河道出口的距离是(L0/2)。
3) 迭代的第2步是把内连接用内生成子替代,后者有1个2阶的叶子。相应地1个2阶径流函数A2f2(t-τ/4)加到公式(5)的右边,正如公式(5)第2行所显示的。时间延迟是(τ/4)是因为从2阶河道的出口到主河道的出口的距离是(L0/4)。
4) 迭代的第3步是内连接被内生成子所替代,其中每一个都有一个3阶的叶子。相应地3阶径流函数A3[f3(t-τ/8) + f3(t-3τ/8)]也应添加到公式(5),正如公式(5)的第3行所显示。时间延迟是(τ/8)和(3τ/8),因为从3阶河道出口到主河道出口的距离分别是(L0/8)和(3L0/8)。其他依次类推。
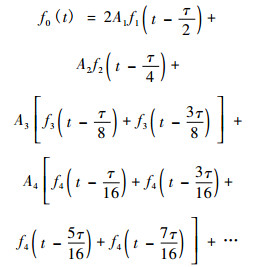
|
(5) |
公式(5)可以归结为
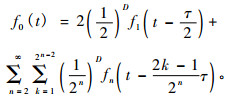
|
(6) |
由于河道结构的自相似性,不难得到各阶归一化径流函数fm(t)的递归关系
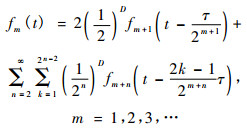
|
(7) |
只要限定最高阶,在个人电脑上编程,很容易自动生成各级递归函数。
1.1.3 面积归一化和分数维D为了得到T1型河网的分数维D,采用面积归一化方法,就是说每一个局部面积之和等于总面积。根据图 3和公式(5),面积之和应该等于1,即:
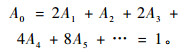
|
(8) |
根据公式(3)可得:
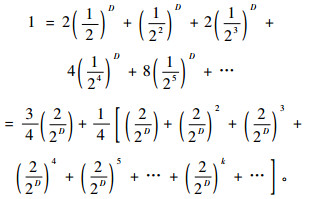
|
(9) |
如果
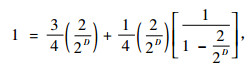
|
(10) |
容易得到D = ln3/ln2 = 1.585 0。它看起来有点像河道空间没有填满的情况:从某个高度向上,河网的分岔停止了,而没有河岔的山坡开始了(Schuler et al., 2001)。河网的分数维D是一个河网充满平面能力的一个量度,它是由河网的分叉性质和单独河道的弯曲性引起的。
1.2 T2型河流的函数递归迭代算法T2由图 4的生成子定义。由于T1和T2之间的相似性,T2型河流的RRF算法的细节描述与T1很相似。
|
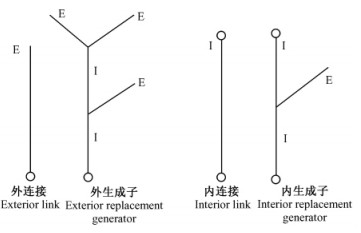
图 4 T2型河网外连接、外生成子、内连接和内生成子图式 Figure 4 Sketch of the exterior link, the exterior replacement generator, the interior link and the interior replacement generator in T2 river |
正如在T1型河道中,在T2型河道中连接也被分类为内连接和外连接,内连接连有2个节点,2个节点分别与上游河道和下游河道联结。外连接只有1个节点在下游端点(图 4)。外连接被有3个外连接和2个内连接的外生成子所替代。而内连接被有1个外连接和2个内连接的内生成子所替代。
1.2.2 函数递归迭代算法T2型河流的RRF算法的过程:
1) 迭代的起点是初始子,它是0阶外连接(图 5)。同时,相应的操作是0级径流函数F0(t) =f0(t)被放在公式(11)的左边,这个0阶径流函数正是我们想要的。
|
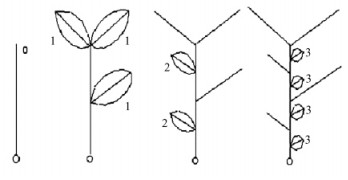
图 5 T2型河网函数递归迭代图式(0 ~ 3级河道) Figure 5 Schetch of recursive replacement of function for the T2 river networks (the rivers of order 0-3) |
2) 迭代的第1步是初始子被外生成子所替代,后者有3个1阶的叶子。对应于这3片叶子,有3个1阶径流函数A1[2f1(t-τ) + f1(t-τ/2)]被放到公式(11)的右边,正如公式(11)第1行所显示的。时间延迟是(τ)和(τ/2),因为从1阶河道出口到主河道出口的距离分别是(L0)和(L0/2)。
3) 迭代的第2步是把内连接用内生成子替代,每个内生成子有1个2阶的叶子。相应地2个2阶径流函数A2[f2(t-τ/4) + f2(t-3τ/4)]应该加到公式(11)的右边,正如公式(11)第2行所显示的。时间延迟是(τ/4)和(3τ/4),因为从2阶河道的出口到主河道的出口的距离分别是(L0/4)和(3L0/4)。
4) 迭代的第3步是内连接被内生成子所替代,其中每个内生成子都有1个3阶的叶子。相应地4个3阶径流函数A3[f3(t-τ/8) + f3(t-3τ/8) +f3(t-5τ/8) + f3(t-7τ/8)]也应添加到公式(11)的右边,正如公式(11)第3行所显示的。时间延迟是(τ/8),(3τ/8),(5τ/8)和(7τ/8),因为从3阶河道出口到主河道出口的距离分别是(L0/8),(3L0/ 8),(5L0/8)和(7L0/8)。其他依次类推。

|
(11) |
公式(11)可以归结为
由于河道结构的自相似性,不难得到各阶归一化径流函数fm(t)的递归关系
1.2.3 面积归一化和分数维D为了得到T2型河网的分数维D,在此也采用面积归一方法,即每一个局部面积的和等于总面积。根据图 5和公式(11),面积和应该等于1,即:

|
(14) |
根据公式(3)可得:
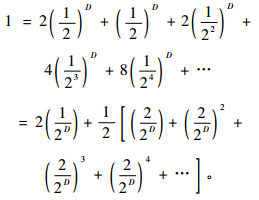
|
(15) |
如果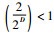
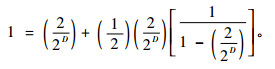
|
(16) |
容易得到D = 2。此结果表明T2型河网空间可能是填满的。如果一个河网的空间真的是填满的,人们可以期望算出河网分数维等于2。某些研究者,包括Mandelbrot(1983)和Tarboton等(1988)相信分数维等于2就是空间填满的情况(Schuller et al., 2001)。
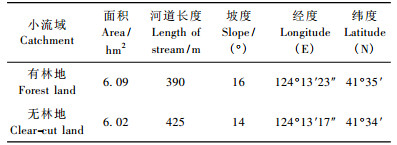
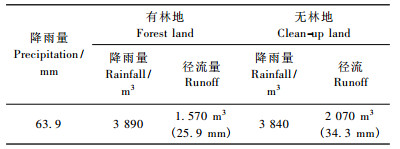
2 RRF算法应用下面,用2种严格自相似河网(T1和T2)演示RRF算法。数据源于东北辽河流域浑河支流社河流域五龙林场有林地和无林地(表 1)在一次降雨过程(1995-08-06-07)中的降雨量和径流数据(表 2)。
|
|
|
|
在一个数学理想化中,严格自相似河网能被生成为无限阶。但实际上真实河流可能被看作不完美的自相似,因为到达某一点上,其结构变得太小而无法继续。在递归关系中(公式6,7,12和13),采用6阶作为最高阶。就是说,用小流域的径流过程函数(除以流域面积)当作第6级归一化径流函数f6(t)。
利用递归关系公式(7)和(13),当有了f6(t),就不难得到f5(t),有了f6(t)和f5(t),就可以得到f4(t),依次类推,最终得到f0(t)。
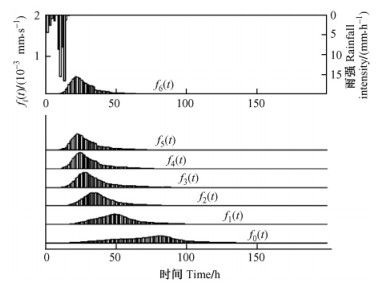
在PC机上用QBASIC程序实现RRF算法。结果显示在图 6~9中。图 6~9中,最上一行倒置柱状图表示降雨过程,第2行曲线表示在最小流域出口处测得的径流函数数据f6(t),第3,4,5,6,7和8行分别表示用RRF计算出的函数f5(t),f4(t),f3(t),f2(t),f1(t)和f0(t)。
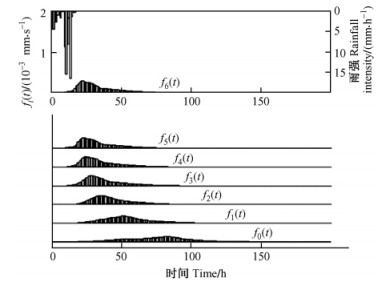
|
图 6 用T1型河网模拟有林地径流 Figure 6 Runoff on the forest land for T1 river network |
|
图 7 用T1型河网模拟无林地径流 Figure 7 Runoff on the clear-cut land for T1 river network |
|
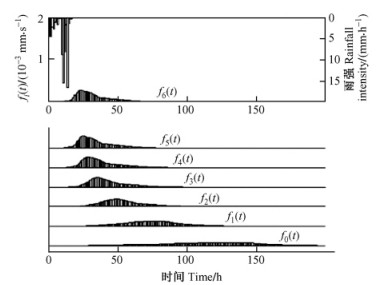
图 8 用T2型河网模拟有林地径流 Figure 8 Runoff on the forest land for T2 river ntwork |
|
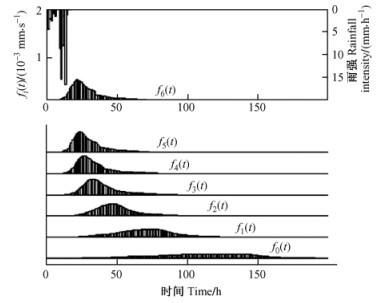
图 9 用T2型河网模拟无林地径流 Figure 9 Runoff on the clear-cut land for T2 river network |
本研究提出的这个算法,将分形河网和降雨-径流响应二者联系起来,我们叫做函数递归迭代算法,即RRF算法。RRF算法是特别为自相似河网(SSN)设计的,它充分地利用了SSN的自相似特征,及计算机的递归计算能力。RRF反映了降雨过程和小流域的水文效应对大河网的径流响应的影响。RRF也反映了水文响应的尺度转换效应。
按文献调研,以前的递归算法,主要是生成分岔河道的几何图形。本研究提出的RRF算法,是第一个能够系统地根据小流域径流函数,计算具有严格自相似结构大流域径流函数的方法,即用递归算法生成分岔河道的径流函数的方法。
比较有林地和无林地,发现有森林的小流域更多地削减了最小流域的峰值和总径流输出,见图 6 ~ 9中f6(t),而按RRF模拟结果,对于自相似河网,无论T1还是T2,都按比例保持了这种削减。另外,与无林地相比较,有林地延展了小流域的径流水文线,见图 6~9中f6(t),而自相似河网则进一步加强了这种延展。还有,出现峰值流量的时间被有林地所推迟,这是一个物理过程,而自相似河网进一步推迟了它,这是一个几何过程。阶数越高的河网,推迟峰值时间越多。
在图 2中,对于T1型河流最大流动距离是L0 = 1,而在图 4中,T2型河流的最大流动距离是2L0 = 2。因此,正如图 6~9分别所示,T2型河流的流动时间要比T1型河流长1倍。当然,这个长与短是相对的,没有绝对意义。
根据RRF模拟结果,森林对小流域径流的有利影响不仅保持,而且被大的自相似河网所进一步强化。
需要解释一下,从图 6~9看不出径流量增大,似乎总径流水量保持不变。这是因为所使用的fi(t)是归一化径流函数,是将某级径流量Fi(t)除以该级流域面积Ai。如果把它们乘以相应流域面积,就可以看到径流量逐渐增大。
图 6~9中的f6(t)就是在最小流域测量的径流函数,逐渐汇聚成f5(t),f4(t),f3(t),f2(t),f1(t)和f0(t),而f0(t)是最大流域的径流函数。这就是尺度变换。
从图 6~9可见,2类不同林地的模拟结果是有区别的,这很合理。因为森林必然要吸收一部分降水量,同时延缓出水过程; 而用T1和T2河道模拟同一种林地,除了相对时间长短不同外,基本上没有区别,这说明模拟结果并不太依赖河道的分岔类型。
Hack J T. 1957. Studies of longitudinal profiles in virginia and maryland, U. S[J]. Geological Survey Professional Papers. |
Horton R E. 1945. Erosional development of streams and their drainage basins: hydrophysical approach to quantitative morphlogy[J]. Geological Society of America Bulletin, 56(3): 275-370. DOI:10.1130/0016-7606(1945)56[275:EDOSAT]2.0.CO;2 |
La Barbara, Rosso R. 1987. Fractal geometry of river networks (abstract)[J]. Eos Transaction of American Geophysical Union, 68(44): 1276. |
La Barbara, Rosso R. 1989. On the fractal dimention of stream networks[J]. Water Resources Research, 25(4): 735-741. DOI:10.1029/WR025i004p00735 |
Mandelbrot B B. 1977. Fractals: form, chance, and dimension[M]. New York: Freeman.
|
Mandelbrot B B. 1977. Fractals: form, chance, and dimension[M]. New York: Freeman.
|
Nikora V I. 1988. Fractal properties of some hydrological objects (in Russion)[J]. Academy of Science of Moldavian SSR, Kishinev. |
Schuller D J, Rao A R, Jeong G D. 2001. Fractal characteristics of danse stream networks[J]. Journal of Hydrology, 343: 1-16. |
Strahler A N. 1952. Hypsometric (area-altitude) analysis of erosional topography[J]. Geological Society of America Bulletin, 63: 1117-1142. DOI:10.1130/0016-7606(1952)63[1117:HAAOET]2.0.CO;2 |
Tarboton D G, Bras R L, Rodriguez-Iterbe I. 1988. The fractal nature of river networks[J]. Water Resources Research, 24(8): 1317-1322. DOI:10.1029/WR024i008p01317 |
Wang P J, Wang R Y. 2002. A generalized width function of fractal river network for the calculation of hydrologic responses[J]. Fractal, 10(2): 157-171. DOI:10.1142/S0218348X02001038 |
Zavoianu I. 1985. Morphometry of Drainage Basins[M]. New York: Elsevier Science.
|
 2010, Vol. 46
2010, Vol. 46