文章信息
- 李春明, 唐守正
- Li Chunming, Tang Shouzheng
- 基于非线性混合模型的落叶松云冷杉林分断面积模型
- The Basal Area Model of Mixed Stands of Larix olgensis, Abies nephrolepis and Picea jezoensis Based on Nonlinear Mixed Model
- 林业科学, 2010, 46(7): 106-113.
- Scientia Silvae Sinicae, 2010, 46(7): 106-113.
-
文章历史
- 收稿日期:2009-04-13
- 修回日期:2009-06-10
-
作者相关文章
林分断面积生长预估模型是描述林木或林分断面积生长变化的方程式,一直是林分生长和收获模型体系的重要组成部分(杜纪山,1999)。断面积预测的可靠性直接影响森林经营决策,因此提高模型的估计精度尤为重要。抚育间伐作为人们干预林分生长的主要营林措施,对林分断面积生长的影响日益受到重视,有必要根据实际情况对间伐林分的断面积进行研究,为定量间伐、生长预测提供科学依据(李春明等,2007)。由于固定样地数据常常有层次结构,使同一样地不同树木间具有相关性。采用连续观测数据,使同一样地或同一树木多次观测值之间具有相关性。因此,这种“样地效应”或“树木效应”使误差不满足独立同分布的假设。其次随机误差至少包括样地间、样地内个体间及同一个体多次重复测量的随机效应。而混合模型作为一种有力的工具用于多层次重复测量数据,通过规定不同的协方差结构来表示相关的误差情况,允许数据间具有相关性及异方差,从而提高预测精度并解释随机误差的来源。此方法既可以反映总体平均变化趋势, 又可以反映个体之间的差异(Little et al., 1996)。近年来,混合模型技术已经广泛应用于森林生长模型中(Tang et al., 2001; 李永慈等, 2004; Zhao et al., 2005; Lynch et al., 2005; Uzoh et al., 2006; 2008; Dorado et al., 2006; Mahadev et al., 2007; Wang et al., 2008; Adame et al., 2008)。
国内外一些学者利用混合模型方法对林分的断面积进行了研究。Fang等(2001b)利用线性混合效应模型方法,考虑了样地的随机效应、误差方差异性及时间序列相关性,模拟了不同经营措施(采伐、施肥和燃烧)下美国乔治亚州和佛罗里达州湿地松(Pinus elliottii)林分的断面积,结果表明:混合模型方法要比传统方法预测的精度高。Budhathoki等(2005)在模拟美国萌芽松(Pinus echinata)断面积生长时考虑了样地的随机效应及误差方差异性,结果认为:当增加随机效应参数数量时能够提高模型的估计精度。李春明(2009)以江西大岗山实验局不同初植密度杉木(Cunninghamia lanceolata)林分为研究对象,选择常用的Richards和Schumacher 2种模型进行断面积模拟,利用最小二乘回归法进行拟合,然后选择预估精度最高的方程作为基础模型,并在此基础上考虑样地效应来构建非线性混合模型,结果表明:与传统的非线性回归方法相比,混合模型大大提高了断面积的估计精度。雷相东等(2009)采用多水平重复测量线性混合模型方法,建立了6个树种(组)单木断面积生长模型,并与传统回归模型方法进行精度比较,结果认为:与传统的固定效应模型相比,混合模型显著地提高了预估精度,模型的决定系数显著提高,而均方根误差和平均绝对残差都显著减少。以上研究都表明:在模拟林分断面积时,混合模型方法要比传统的回归方法精度高。
本文以吉林省汪清林业局金沟岭林场20块落叶松云冷杉林分为研究对象。首先利用非线性最小二乘方法从4个常用的Richards和Schumacher断面积模型中找出模拟精度最高的模型作为基础模型,然后把20块样地数据分成2部分,一部分共15块作为模拟数据,另一部分5块作为验证数据,利用基础模型及模拟数据构建非线性混合效应模型,考虑样地效应,采用SAS软件进行模拟。选择模型收敛及对数似然值(-2log Likelihood)、AIC(akaike information criterion)和BIC(bayesian information criterion)值最小的混合模型作为最优模型,在此基础上考虑断面积连续观测数据时间上的序列相关性,并把间伐强度以哑变量形式加入到模型中,最后进行混合模型的模拟。利用验证数据进行验证,选择确定系数(R2)、均方根误差(RMSE)、平均绝对残差(|E|)等3个评价指标对考虑样地效应、时间序列相关性及间伐强度的混合模型模拟结果与传统非线性回归模拟方法进行精度比较。
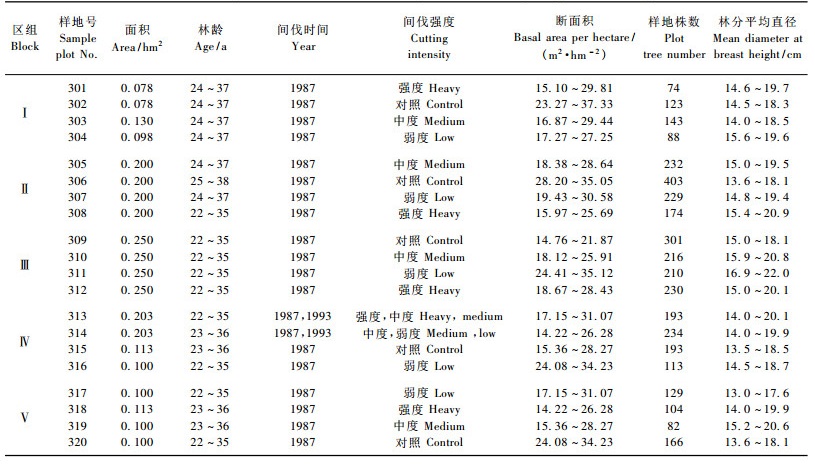
1 材料本研究样地数据来自位于吉林省汪清林业局金沟岭林场境内。该林场所处的地理位置为130°5′—130°20′E,43°17′—43°25′N,海拔550~1 100 m。用来建立模型的数据其起源为1964—1967年营造的人工落叶松纯林,经过多年的演变,大部分已经成为落叶松云冷杉针阔混交林。用于本研究的20块落叶松云冷杉样地共进行了7次调查(1986,1988,1990,1992,1994,1997,1999年)。按照区组试验设计的方法,样地共进行4个处理5个重复,每个处理包括3种间伐强度和1个对照,其中3种间伐强度为弱度、中度和强度,分别为蓄积的20%,30%和40%。落叶松树种的年龄作为样地林分的年龄。样地中针叶树种包括长白落叶松(Larix olgensis)、冷杉(Abies nephrolepis)、云杉(Picea jezoensis)和红松(Pinus koraiensis);阔叶树种包括椴(Tilia amurensis)、白桦(Betula platyphylla)、水曲柳(Fraxinus mandshurica)、胡桃楸(Juglans mandshurica)、黄菠萝(Phellodendron amurense)、色木槭(Acer mono)和榆(Ulmus propinqua)等树种。
为了研究间伐对断面积的影响,每种间伐强度选择了1块样地作为验证,因此从每个区组内选择了1块样地共5块样地即301, 305, 309, 313和317样地数据作为本研究的验证数据,其余15块样地数据作为建模数据,具体见表 1。
|
|
非线性混合模型是通过考虑回归函数依赖于固定和随机效应的非线性关系而建立的。以本研究为例,单水平非线性混合效应模型的形式如式(1)(Pinheiro et al., 2000):
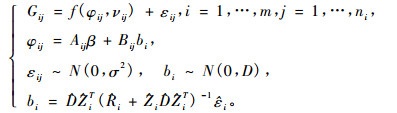
|
(1) |
式中:Gij是第i个样地第j次观测的因变量值,m是研究的样地数量,ni是第i个样地连续观测的次数,f是包括参数向量φij和观测变量νij的可微函数,εij是服从正态分布的误差项,β是(p×1)维固定效应向量,bi是带有方差协方差矩阵D的(q×1)维随机效应向量,Aij和Bij是相应的设计矩阵,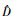
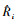
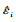
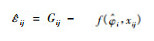
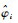
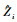
研究林分断面积生长的模型种类很多,例如Logistic方程、Schumacher方程、Gompertz方程、Richards方程和Korf方程等。断面积生长预估模型要达到良好的拟合效果,主要应包含地位质量指标、年龄和密度指标这3个自变量(唐守正,1991;杜纪山等,1997)。在模型形式上,Richards方程因其具有较好的数学性质和生物学意义而成为常用的断面积生长预估模型(Pienaar et al., 1984); 而Schumacher模型在模拟过程中容易收敛,很方便获取模拟结果,得到了众多学者的推崇。本文在预估林分断面积时选择了Richards和Schumacher式作为基本模型形式,通过地位质量指标、年龄和密度指标这3个自变量的变化来预估林分断面积。具体模型形式如下:
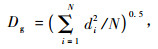
|
(2) |
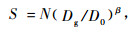
|
(3) |
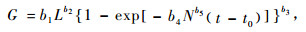
|
(4) |
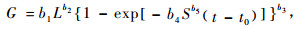
|
(5) |
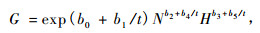
|
(6) |
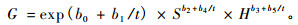
|
(7) |
式中:G为年龄t时的断面积, L为地位指数, S为林分密度指数,N为单位面积株数,H为林分优势木平均高,t为林分年龄,t0为林木生长到胸高时的年龄(本研究中t0取4年), di为每木胸径,Dg为林分平方平均直径,D0为标准直径,β为长白落叶松自稀疏率。本研究长白落叶松的标准直径和自然稀疏率采用杜纪山(1999)的研究结果:D0=20 cm, β=1.58。b0, b1, b2, b3, b4, b5为待估参数。
2.3 混合模型结构在构建混合模型之前,需要确定以下2个结构(Fang et al., 2001a):
1) 样地内方差协方差结构(Ri) 样地内方差协方差结构也称为误差效应方差协方差结构。为了确定样地内的方差协方差结构,必须解决异方差和自相关2方面的问题。对固定样地进行长期观测的森林生长收获数据通常都存在自相关和异方差问题。为了解决样地内误差的异质性和自相关问题,在林业上通常利用式(8)进行描述(Davidian et al., 1995;Fang et al., 2001a;Wang et al., 2007):
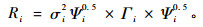
|
(8) |
式中:Ri是样地内方差协方差矩阵,σi2为未知样地i的残差方差,Ψi为描述样地内误差方差的异质性的对角矩阵,Γi是描述误差效应自相关结构矩阵。
2) 样地间方差协方差结构(D) 样地间方差协方差结构也称为随机效应方差协方差结构。样地间的方差协方差结构反映了样地之间的变化和差异性。在确定样地间方差协方差结构之前,需要确定哪个参数为固定效应哪个为混合效应,这一般依赖于所研究的数据。如果没有关于随机效应方差协方差结构的先验知识,Pinheiro等(2000)建议模型中所有的参数首先应全部看成是混合的,然后再分别进行参数拟合,最后选择模型收敛并且模拟精度较高的形式来进行效果评价。本文按照此方法进行参数选择和模拟,并选择常用的无结构矩阵模型(UN)及复合对称矩阵模型(CS)作为随机效应参数方差协方差矩阵。
2.4 模型精度比较利用确定系数(R2)、平均绝对残差(|E|)及均方根误差(RMSE)等3个模型精度评价指标对模拟结果进行效果评价,具体公式见式(9~11)。RMSE和|E值越小而R2值越大说明模型的精度越高(Calama et al., 2004)。
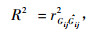
|
(9) |
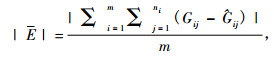
|
(10) |
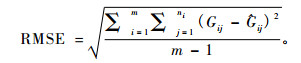
|
(11) |
式中: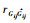
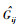
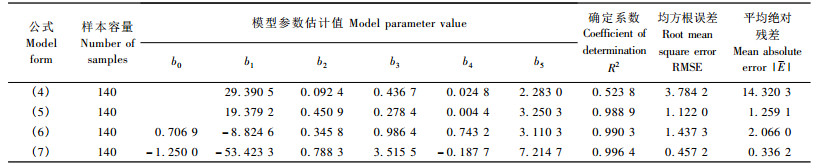
利用SAS软件对式(4~7)4个模型采用最小二乘回归参数估计方法进行拟合,选择确定系数、均方根误差及平均绝对残差对模拟结果进行比较分析,结果见表 2。从表 2可以看出,自变量包括林分密度指数、林龄及优势木平均高的Schumacher型断面积模型即式(7)的确定系数最高,而均方根误差和平均绝对残差最小,因此选择式(7)作为构建混合模型的基础模型。
|
|
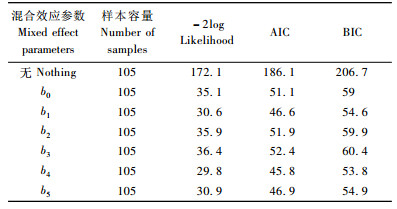
作者尝试了不同混合效应参数的组合进行混合模型的模拟,但由于本研究在2个以上参数作为混合效应参数情况下考虑时间序列相关性及间伐影响时均不能收敛,因此只把式(7)中的单个参数作为混合效应参数,考虑林分的样地效应,利用SAS软件进行非线性混合模型的模拟,计算结果如表 3。
|
|
表 3的模拟结果说明:无论哪个参数作为混合效应参数,其模拟效果都要比传统最小二乘方法效果好,另外参数b4作为混合效应参数,无论对数似然值、AIC或BIC值都最小,因此最后确定的混合模型的基本形式如式(12):
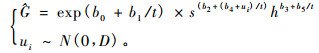
|
(12) |
式中:ui为随机效应参数,本研究中i=1, 2, …, 15。
3.3 考虑误差结构矩阵在利用混合模型方法模拟林分断面积时,不可忽视的2个问题就是误差的异方差和连续观测数据的自相关性。通常判断是否存在异方差最直观的方法就是利用断面积残差分布图,图 1A,B分别是传统回归模型与b4作为混合效应参数的断面积残差分布结果。
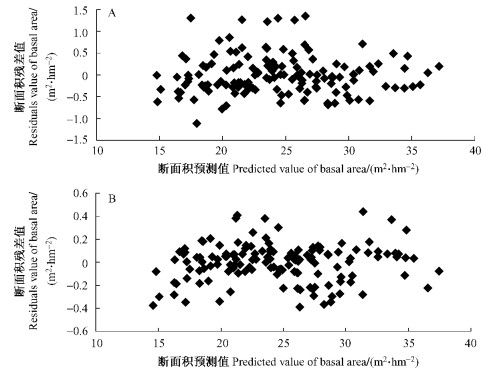
|
图 1 基于传统回归方法和混合模型方法的断面积残差与断面积预测值关系 Figure 1 The residuals versus predicted value of basal area based on ordinary regression analysis and mixed model A.传统回归方法Ordinary regression method; B.混合模型方法Mixed model. |
虽然图 1A,B的残差都不随估计值的增大而增大,但是图 1B表示出估计的断面积残差值比图 1A的残差值分布范围要小的多,因此异方差的影响在本研究中并不考虑,即Ψi0.5=Ii。本研究所用的断面积数据是连续7次观测,数据间存在着时间序列相关性。为了表达样地内的时间序列相关性,一阶自回归矩阵模型[AR(1)]、一阶自回归与滑动平均模型相结合的矩阵模型[ARMA(1, 1)]及复合对称矩阵模型(CS)经常被用在森林生长收获模拟中(Wang et al., 2007)。本文采用这3个自相关矩阵模型来表述林分断面积的自相关结构,具体模拟结果如表 4。
|
|
表 4的结果表明:选择适当的时间序列自相关结构能够提高模型的估计精度,采用AR(1)和ARMA(1, 1) 2个结构比不考虑时间序列的自相关结构精度要高, 而且采用AR(1)误差结构矩阵的混合模型3个指标值均最小,因此本研究采用AR(1)来描述落叶松云冷杉林分的时间序列自相关结构矩阵。
3.4 间伐强度对断面积的影响间伐对林分的生长具有很大的影响,尤其对林木的胸径生长有直接的影响,而断面积是与胸径有着密不可分的关系,因此在模拟林分断面积时不可忽视间伐强度。本研究中间伐强度用哑变量的形式表达。综合前面的研究,最后确定的落叶松云冷杉林分断面积混合效应模型如式(13):
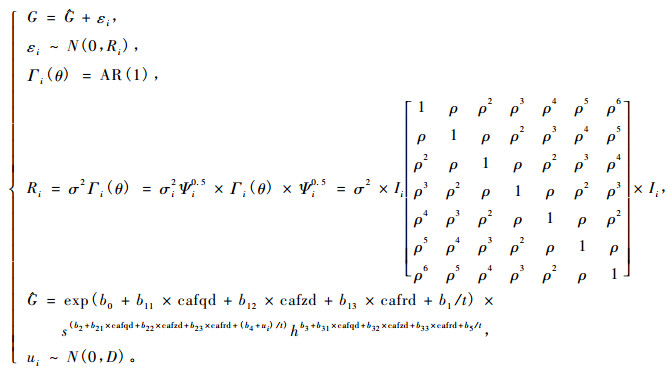
|
(13) |
式中:cafqd指强度间伐,cafzd指中度间伐,cafrd为弱度间伐。如某样地为强度间伐,则cafqd为1,cafzd和cafrd为0,中度间伐则cafzd为1,其余为0,弱度间伐依次类推,对照样地这3个变量都为0。b11,b12,b13,b21,b22,b23,b31,b32,b33及ρ为待估参数,其他参数和变量同前面描述。
利用SAS软件中的MACRO MIXED模块对上述混合模型进行模拟,结果如下:
1) 固定效应参数:
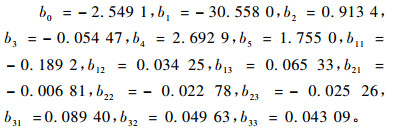
|
2) 样地间随机效应方差协方差矩阵:
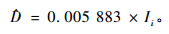
|
3) 样地内误差效应方差协方差矩阵:
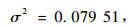
|
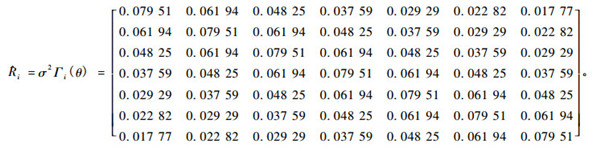
|
4) 模拟评价指标:
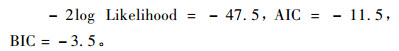
|
从对数似然值、AIC值和BIC值3个指标值来看,在模拟落叶松云冷杉间伐林分时考虑间伐强度的影响要比不考虑间伐强度的影响的模拟效果好,间伐强度以哑变量形式体现在模型中能够很好地表述间伐对断面积的影响。
3.5 模型验证及精度比较对剩余的5块落叶松云冷杉林分进行验证,根据式(1)中的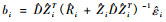
|
|
从模拟结果看:考虑样地效应、时间序列自相关性及间伐的混合模型其确定系数高于固定效应模型,而均方根误差和平均绝对残差小于固定效应,一方面说明混合模型的模拟精度高于固定效应模型,另一方面计算出的随机参数也能够体现各样地之间断面积的差异性。
为了更直观地描述随机效应参数ui的计算过程,以301样地为例,根据7次测量值(16.00,18.61,21.09,23.61,25.41,28.07,29.85),首先求出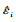
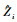
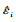
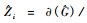
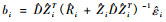
1) 利用确定系数、均方根误差和平均绝对残差来评价传统最小二乘模拟结果表明:以林龄、优势木平均高和林分密度指数为自变量的Schumacher模型精度高于其他3个模型的精度。
2) Schumacher模型中无论哪个参数作为混合效应参数,模拟的效果都好于传统的回归估计方法,而b4作为混合效应参数的模拟精度最高,并且减小了误差的异方差问题。
3) 在模拟固定样地连续观测数据时,选择适合的时间序列自相关矩阵模型不仅能提高模型的模拟精度,而且能很好地描述连续观测数据间误差分布情况。AR(1)矩阵模型和ARMA(1, 1)在描述断面积连续观测中的时间序列误差方差协方差结构矩阵方面精度高于不考虑自相关误差矩阵,而尤以AR(1)矩阵模型精度最高。另外在模拟过程中,同时考虑样地的随机效应、时间序列的自相关误差矩阵及间伐强度明显提高了混合模型的预测精度。
4) 考虑到样本量不足的问题,本研究没有把落叶松云冷杉林分各树种的断面积单独进行模拟或者考虑树种的随机效应,而只进行了总体的模拟。如采用混合模型方法进行单独模拟或者考虑树种的随机效应模拟精度可能更高。因此,需要在继续增大样本量的基础上作进一步的研究。
杜纪山, 唐守正. 1997. 林分断面积生长模型研究综述[J]. 林业科学研究, 10(6): 599-606. |
杜纪山. 1999. 天然林区林木生长模型的研究[J]. 中国林业科学研究院博士后研究工作报告: 14. |
雷相东, 李永慈, 向玮. 2009. 基于混合模型的单木断面积生长模型[J]. 林业科学, 45(1): 74-80. DOI:10.11707/j.1001-7488.20090113 |
李春明, 杜纪山, 张会儒. 2007. 抚育间伐对人工落叶松断面积和蓄积生长的影响[J]. 林业资源管理, (3): 90-93. |
李春明. 2009. 利用非线性混合模型进行杉木林分断面积生长模拟研究[J]. 北京林业大学学报, 31(1): 44-49. |
李永慈, 唐守正. 2004. 用Mixed和Nlmixed过程建立混合生长模型[J]. 林业科学研究, 17(3): 279-283. |
唐守正. 1991. 广西大青山马尾松全林整体生长模型及其应用[J]. 林业科学研究, 4(增): 8-13. |
Adame P, Rio M D, Canellas I. 2008. A mixed nonlinear height-diameter model for Pyrenean oak(Quercus pyrenaica Willd.)[J]. Forest Ecology and Management, 256: 88-98. DOI:10.1016/j.foreco.2008.04.006 |
Budhathoki C B, Lynch T B, Guldin J M.2005.Individual tree growth models for natural even-aged Shortleaf Pine(Pinus echinata Mill.). Proceedings of the 13th Biennial Southern Silvicultural Conference, Memphis, TN.
|
Calama R, Montero G. 2004. Interregional nonlinear height-diameter model with random coefficients for stone pine in Spain[J]. Canadian Journal of Forest Research, 34: 150-163. DOI:10.1139/x03-199 |
Davidian M, Giltinan D.1995.Nonlinear models for repeated measurement data.Chapman & Hall, London.
|
Dorado F C, Ulises D A, Marcos B A, et al. 2006. A generalized height-diameter model including random components for radiata pine plantations in northwestern Spain[J]. Forest Ecology and Management, 229: 202-213. DOI:10.1016/j.foreco.2006.04.028 |
Fang Z, Baley R L. 2001a. Nonlinear mixed effects modeling for slash pine dominant height growth following intensive silvicultural treatments[J]. Forest Science, 47: 287-300. |
Fang Z, Bailey R L, Shiver B D. 2001b. A multivariate simultaneous prediction system for stand growth and yield with fixed and random effects[J]. Forest Science, 47: 550-562. |
Little R C, Milliken G A, Stroup W W, et al. 1996. SAS system for mixed models[M]. Cary North Carolina, USA: SAS institute Inc.
|
Lynch T B, Holley A G, Stevenson D J. 2005. A random-parameter height-diameter model for Cherry-bark Oak[J]. Southern Journal of Applied Forest, 29: 22-26. |
Mahadev S, John P. 2007. Height-diameter equations for boreal tree species in Ontario using a mixed-effects modeling approach[J]. Forest Ecology and Management, 249: 187-198. DOI:10.1016/j.foreco.2007.05.006 |
Pienaar L V, Shiver B D. 1984. An analysis and models of basal area growth in 45-year-old unthinned and thinned slash pine plantation plots[J]. Forest Science, 30(4): 933-942. |
Pinheiro J C, Bates D M. 2000. Mixed effects models in S and S-plus[M]. New York: Springer Verlag.
|
Tang S Z, Meng F R. 2001. Analyzing parameters of growth and yield models for Chinese Fir provenances with a linear mixed approach[J]. Silvae Genetica, 50: 140-145. |
Uzoh F C C, Oliver W W. 2006. Individual tree height increment model for managed even-aged stands of Ponderosa Pine throughout the western United States using linear mixed effects models[J]. Forest Ecology and Management, 221: 147-154. DOI:10.1016/j.foreco.2005.09.012 |
Uzoh F C C, Oliver W W. 2008. Individual tree diameter increment model for managed even-aged stands of Ponderosa Pine throughout the western United States using a multilevel linear mixed effects models[J]. Forest Ecology and Management, 256: 438-445. DOI:10.1016/j.foreco.2008.04.046 |
Wang M L, Borders B E, Zhao D H. 2008. An empirical comparison of two subject-specific approaches to dominant heights modeling: the dummy variable method and the mixed model method[J]. Forest Ecology and Management, 255: 2659-2669. DOI:10.1016/j.foreco.2008.01.030 |
Wang Y, Valerie M L, Thomas G B. 2007. Modelling and prediction of dominant height and site index of Eucalyptus globules plantations using a nonlinear mixed-effects model approach[J]. Canadian Journal of Forest Research, 37: 1390-1403. DOI:10.1139/X06-282 |
Zhao D, Wilson M, Borders B E. 2005. Modeling response curves and testing treatment effects in repeated measures experiments: a multilevel nonlinear mixed-effects model approach[J]. Canadian Journal of Forest Research, 35: 122-132. DOI:10.1139/x04-163 |
 2010, Vol. 46
2010, Vol. 46