利用Hansen-Hurwitz(Hansen et al., 1943)估计量和Horvitz-Thompson(Horvitz et al., 1952)估计量，Thompson (1990)首次提出了自适应群团抽样(adaptive cluster sampling，简称ACS)，即基于修正Hansen-Hurwitz估计量的ACS、基于修正Horvitz-Thompson估计量的ACS。随后，出现了多种自适应群团抽样设计，分层自适应群团抽样(Thompson，1991)、两阶段自适应群团抽样(Salehi et al., 1997)和两相自适应群团抽样(Felix-Medina et al., 2004)。

Thompson(1991)利用最初交叉次数的期望(expected numbers of initial intersection)、Hansen-Hurwitz估计量和最初交叉概率(initial intersection probabilities)构造了4种不同的分层适应性群团抽样设计，即跨越边界基于Hansen-Hurwitz估计量的分层ACSI、跨越边界基于Hansen-Hurwitz估计量的分层ACSⅡ、不跨越边界基于修正Hansen-Hurwitz估计量的分层ACS、跨越边界基于修正Horvitz-Thompson估计量的分层ACS。它结合了传统分层抽样和适应性群团抽样的优点。目前，传统的分层抽样研究比较多，然而，关于分层适应性群团抽样的研究非常少。

本研究利用网络交叉包含概率，提出了一种新的分层适应性群团抽样方法，不跨越边界的基于修正Horvitz-Thompson估计量的分层ACS，给出估计量公式，并证明了其无偏性。然后，以内蒙古磴口县巴彦高勒镇西南约8 km的乌兰布和沙漠边缘地区为研究区, 该地区植被花棒(Hedysarum scoparium)呈稀少、群团状分布，以花棒密度为研究对象，利用9种抽样方法：分层简单随机抽样(其均值估计为t₁、相应的方差估计为v₁)、跨越边界基于Hansen-Hurwitz估计量的分层ACSI(其均值估计为t₂、相应的方差估计为v₂)、跨越边界基于Hansen-Hurwitz估计量的分层ACSⅡ(其均值估计为t′₂、相应的方差估计为v′₂)、不跨越边界基于修正Hansen-Hurwitz估计量的分层ACS(其均值估计为t″₂、相应的方差估计为v″₂)、跨越边界基于修正Horvitz-Thompson估计量的分层ACS(其均值估计为t₃、相应的方差估计为v₃)、不跨越边界基于修正Horvitz-Thompson估计量的分层ACS(其均值估计为t₄、相应的方差估计为v₄)、简单随机抽样(其均值估计为t₅、相应的方差估计为v₅)、基于修正Hansen-Hurwitz估计量的ACS(其均值估计为t₆、相应的方差估计为v₆)和基于修正Horvitz-Thompson估计量的ACS(其均值估计为t₇、相应的方差估计为v₇)，进行了抽样模拟试验，这9种抽样方法的最初样本均采用不放回抽取，对比分析了9种抽样方法的精度，寻求最适宜的抽样方法，用以指导研究区稀少、群团状植被的调查。

1 不跨越边界基于修正Horvitz-Thompson估计量的分层ACS 1.1 抽样设计

邻域或邻近(Neighborhood)、网络(Network)、边缘单元(edge unit)、群团(cluster)、临界值(C_α)、自适应群团抽样(ACS)的概念和自适应群团抽样的相关估计量公式见Thompson(1990)、雷渊才等(2007)，本研究采用一阶邻域。

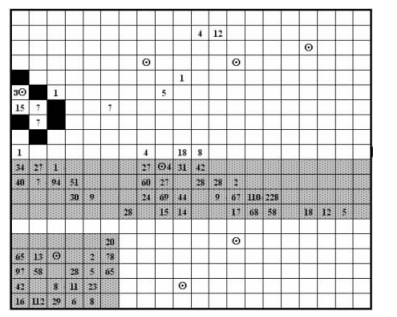
现以图 1为例说明不跨越边界的分层自适应群团抽样方法。第1阶段，假设总体中有N个单元，将总体划分为L个层(strata)，各层标记为h(h=1, 2, …, N)，各层包括N_h个单元，从层h中，采取不放回简单随机抽样抽取n_h个单元，各层分别独立进行抽样(如图 1，总体单元N=400，层L=2，单元格背景为灰白色且带点的所有单元为第1层，其余的为第2层，第1层的样本单元数N₁=110，第2层的样本单元数N₂=290。图中标记⊙所在的单元即为最初抽取的样本单元，Σn_h=8，最初样本量为8，网格内的数字表示单元属性值)。第2阶段，按照适应性抽样规则，当最初样本单元值满足条件C (μ_hi表示第h层中第i个单元，相对应的感兴趣的目标变量值为y_hi。单元属性值y_hi≥c_α=0，c_α为临界值)时，该单元的相邻单元也入样，如果相邻单元也满足条件，且相邻单元与其在同一层内，则该相邻单元继续入样，直至遇到不满足条件的单元为止(如图 1, 抽中了2个单元值大于临界值的网络, 被深黑色背景的单元所包围的单元为抽中的网络之一)。这个过程就称不跨越边界的分层适应性群团抽样。

最初样本量与最终样本：抽取的最初样本量为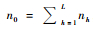，最终样本为最初样本再加上按照适应性抽样规则抽取的样本单元。

不跨越边界的分层自适应群团抽样程序：1)最初样本单元的抽取，通常采用不放回抽样对各个层分别独立抽取最初样本单元，如图 1，第1层中抽取的最初样本单元数n₁=2，第2层中抽取的最初样本单元数n₂=6，所以，最初样本量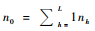=(2+6)=8; 2)临界值的设置和邻域的定义(如一阶邻域)；3)以最初样本单元为中心，按照分层自适应群团抽样扩充原则选取额外单元，即得8个网络；4)估计总体均值或总体总和及其相应的方差。

1.2 估计量的提出与证明

考虑到群团不跨越层的边界，将总体划分为K个独立的网络。令y′_hi为第h层第i个网络单元值之和, x_hi为第h层第i个网络的单元数。α_hi为第h层第i个网络的交叉包含概率，α_hij为最初样本单元与第h层第i个网络和第h层第j网络都相交的联合交叉包含概率。由Thompson(1990)中的包含概率和交叉包含概率的计算公式可得： 。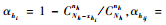

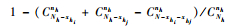
令z_hi和z_hj为Bernoulli随机变量，如果最初样本单元与第h层第i个网络相交，则z_hi=1，否则，z_hi=0;如果最初样本单元与第h层第j个网络相交，则z_hj=1，否则，z_hj=0。由Bernoulli随机变量性质得，E(z_hi) = n_hα_hi。

由Horvitz-Thompson估计量和简单分层估计量，得总体均值估计量：

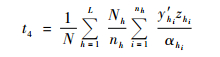
(1)

=总体均值。因此，t₄为总体均值的无偏估计。t₄的方差：

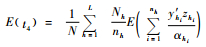
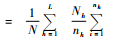
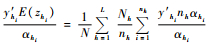
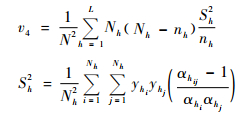
(2)

将样本方差s_h²代替S_h²，即可得t₄方差无偏估计，

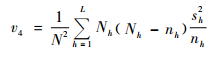
(3)

其中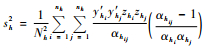，，显然，s_h²为层方差无偏估计，将第h层看作亚总体，证明见Thompson(1990)，可以得知t₄和v₄是无偏的。y′_hi和y′_hj为网络i和网络j的单元值之和。

由这种设计的估计量公式的推导过程，可以得知，它是一种基于Horvitz-Thompson分层自适应群团抽样估计量，因此称之为修正的Horvitz-Thompson估计量。

2 研究区概况与数据采集 2.1 研究区概况

研究地点位于内蒙古西部的磴口县，属于黄河河套地区，灌溉农业发达，境内自然环境分割明显，西部为沙漠戈壁。研究区选在内蒙古西部磴口县巴彦高勒镇西南约8 km黄河西岸绿洲向乌兰布和沙漠过渡的沙漠区，位于农垦区与沙漠交界处，分布有典型的沙地植被，是林业治沙技术试验区。研究区主要乔木树种为沙枣(Elaeagnus angustifolia), 主要灌木树种有白刺(Nitraria tangtorum)、梭梭(Haloxylon ammodendron)、柽柳(Tamarix chinensis)、花棒(Hedysarum scoparium)、盐爪爪(Kalidium foliatum)、柠条锦鸡儿(Caragana korshinskii)和沙蒿(Artemisia ordosica)等。主要草本植物有沙米(Agriophyllum squarrosum)、芦苇(Phragmites australis)、沙鞭(Psammochloa villosa)和沙地旋覆花(Inula salsoloides)等。

2.2 样地设置与数据采集

首先在调查区范围内，选择具有稀少群团状植被的大样地，其面积为1 000 m×1 000 m，将该大样地划分为100块面积为100 m×100 m样地。再将每个样地划分为100个10 m×10 m的小样方。以样地西南角点为原点，测量小样方植株的位置。

调查内容包括100 m×100 m样地的编号、样地面积、每个样地4个地面控制点的三维地理坐标、样地在大样地的位置图、小地形、土壤类型、土层厚度(cm)、优势种、植被起源、树种、权属、造林时间、株行距、植被类型、调查者、调查日期等。以每个小样方(10 m×10 m)为单位进行花棒株数密度的调查，经过调查得大样地花棒总株数为2 107株。

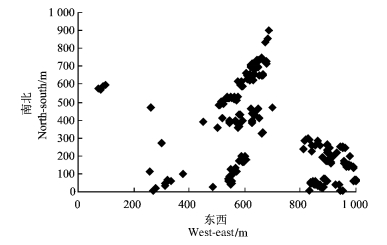
本研究以花棒密度数据作为研究总体，其在大样地中的位置分布状况如图 2。由此图分析可以得知：花棒分布稀少、集聚成群且分布广泛。

3 模拟抽样试验设计方案

邻域的定义采用一阶邻域，临界值C_α=0，扩充条件C＞C_α。

对比各抽样方法的前提是最初样本相同，最初样本的选取均采用不放回简单随机抽样，简单随机抽样的自适应群团抽样的原理与方法见Thompson(1990)和雷渊才等(2007)。

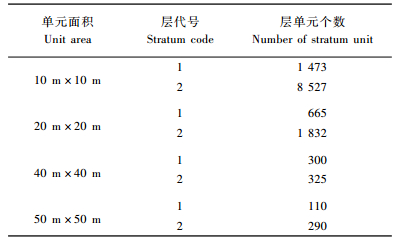
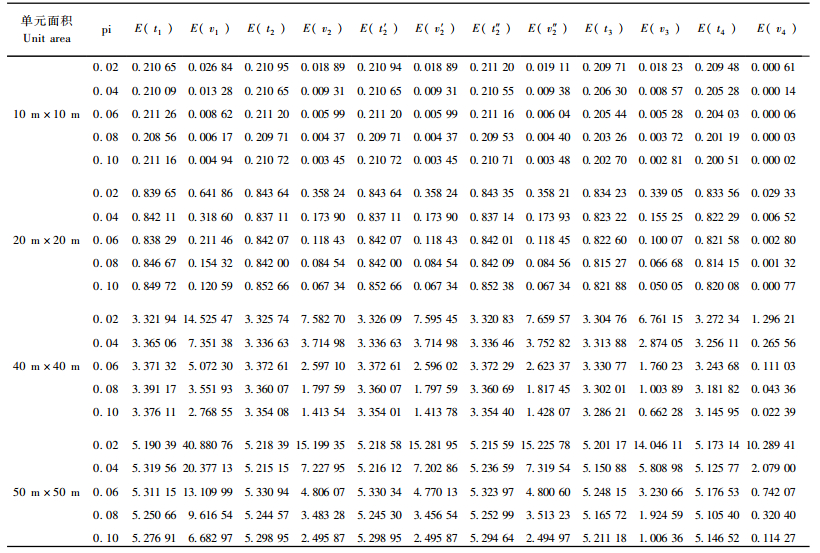
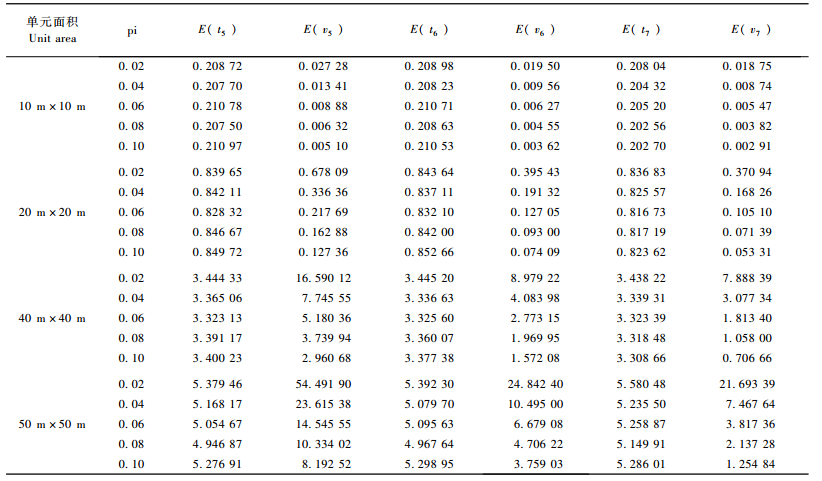
单元面积、总体特征和总体划分的层数等见表 1。对总体，采取不同大小的抽样比pi (pi=0.02, 0.04, 0.06, 0.08和0.1)，各种抽样比均进行5 000次重复抽样试验。各层参数信息见表 2，为了更直观地理解分层参数信息，请参考图 1，图 1即是单元面积为50 m×50 m的总体(抽样比为0.02)。

本次抽样采用的模拟工具是自编的抽样程序，开发语言为VB6.0。

4 结果与分析 4.1 分层抽样设计的样本均值与方差分析

考虑对总体进行分层的情况，由表 1和3可以得知6种类型估计量的均值和方差估计均值的变化呈现一定的规律：1)当单元面积为10 m×10 m、20 m×20 m、40 m×40 m和50 m×50 m时，各种估计量的均值均非常接近于相应的总体均值，6种均值估计量的相对误差变化范围分别为：0.004%~1.464%，0.009%~1.338%，0.009%~1.338%，0.005%~1.494%，0.367%~3.797%和0.579%~6.682%; 2)当单元面积为10 m×10 m, 20 m×20 m, 40 m×40 m和50 m×50 m时，E(v₄)＜E(v₃)＜E(v₂)＜E(v′₂)＜E(v″₂)＜E(v₁), 且E(v₂), E(v′₂)和E(v″₂)的差异非常小，这是因为当各层样本量一致时，E(t₂)=E(t′₂)，E(v₂)=E(v′₂)，在这种条件下，如果抽取的网络(或群团)没有跨越层的边界，E(t₂)=E(t′₂)=E(t″₂)，E(v₂)=E(v′₂)=E(v″₂)；3)当单元大小相同时，随着抽样比的增加，6种估计量的均值方差均逐渐变小；4)当抽样比相等时，随着单元面积变大，6种估计量的均值方差逐渐变大。

4.2 不分层抽样设计的样本均值与方差分析

考虑对总体不进行分层的情况，由表 1和4可以得知3种类型估计量的均值和方差估计均值的变化呈现一定的规律：1)当单元面积为10 m×10 m、20 m×20 m、40 m×40 m和50 m×50 m时，各种估计量的均值均非常接近于相应的总体均值，3种均值估计量的相对误差分别为0.038%~6.087%，0.005%~5.693%和0.164%~5.942%；2)当单元面积为10 m×10 m, 20 m×20 m, 40 m×40 m和50 m×50 m时，E(v₇)＜E(v₆)＜E(v₅)；3)当单元面积相同时，随着抽样比的增加，3种估计量的抽样效率均逐渐增加；4)当抽样比相等时，随着单元大小的增加，3种估计量的抽样效率均递减。

5 结论

以花棒密度为研究对象，通过对9种抽样方法(简单随机抽样、分层简单随机抽样、基于修正Hansen-Hurwitz估计量的ACS、基于修正Horvitz-Thompson估计量的ACS、跨越边界基于Hansen-Hurwitz估计量的分层ACSI、跨越边界基于Hansen-Hurwitz估计量的分层ACSⅡ、不跨越边界基于修正Hansen-Hurwitz估计量的分层ACS、跨越边界基于修正Horvitz-Thompson估计量的分层ACS、不跨越边界基于修正Horvitz-Thompson估计量的分层ACS)的比较得出以下结论：

1) 不跨越边界基于修正Horvitz-Thompson估计量的分层ACS的效率最高，简单随机抽样的效率最低；

2) 分层的抽样方法优于不分层的抽样方法；

3) 当单元面积相同时，随着抽样比的增加，9种估计量的抽样效率均逐渐增加；

4) 当抽样比相等时，随着单元面积的增加，9种估计量的抽样效率均递减。