近几十年，木材无损检测一直是中外学者研究的热点，学者也一直不断地探索新的更适合于木材检测的方法(王立海等, 2001; 戚大伟等, 2006; Ross et al., 1994)。近年来，模态分析技术由于其在桥梁损伤、机械故障等领域的成功应用(刘春城等, 2009; Cornwell et al., 1999; Ratcliffe, 2000)，这一技术也逐渐被引入到木材检测领域中。然而，通过试验模态分析技术获取的固有频率等模态参数，其本身并不能直观地对木材缺陷进行定量识别，因此需要借助适合的数据处理方法。

BP神经网络是迄今为止应用最为广泛的人工神经网络之一，已经被广泛应用于模式识别与分类、函数逼近以及故障检测中(周开利等, 2006; 王立海等, 2007; 闻新等, 2003)。陆秋海等(1998)利用模态分析方法获取了滚动轴承的固有频率，并采用BP网络对轴承故障进行了分类诊断，结果表明BP网络分类效果良好。苏娟等(1999)采用试验模态分析与神经网络相结合的方法对截面开口槽形梁地损伤进行了研究，结果证明神经网络法与试验模态分析技术相结合检测结构损伤是可行的。万小朋等(2003)将优化的BP网络和固有频率相结合成功地对矩形梁结构损伤程度进行了定量识别。上述研究均表明BP神经网络可以通过对大量样本数据的训练，形成一个准确反映样本数据内部规律的网络，进而可利用这一网络对待判定的数据进行判别。BP网络的这一特点正好满足模态参数数据处理的要求；同时，BP网络一般为多层神经网络，而多层网络可以很好地解决非线性问题，而这也正好满足木材缺陷特征较为复杂的要求。本文将尝试采用模态分析与BP神经网络相结合的方法对木材孔洞缺陷进行定性、定位、定量识别。

1 构造基于固有频率的缺陷识别指标

忽略阻尼的影响，结构的特征值方程为KΦ=ω²MΦ，令λ=ω²，则：

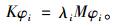
(1)

式中:λ_i是特征值，φ_i是第i阶正则化位移模态矢量。缺陷会使结构刚度明显降低，而对质量分布影响较小，因而当结构的刚度矩阵产生一个很小的摄动量δK时，相应地会使λ_i和φ_i产生δλ_i和δφ_i的改变量。含有缺陷的结构运动方程的摄动方程为:

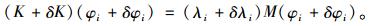
(2)

仅保留1阶项，并利用(1)式，可得：

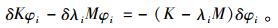
(3)

用φ_i^T左乘(3)式，并利用M，K为对称矩阵及(1)式，可得：

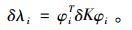
(4)

当结构含有缺陷时，δK≤0，所以δλ_i≤0。又λ=ω²，所以δω≤0。这就说明了当一个完好的结构在某处含有缺陷时，其频率将减小。

从(4)式中还可清楚地看出，频率是由结构缺陷大小和缺陷位置复合决定的，如果缺陷位置一定，则缺陷程度越大频率的变化量越大。缺陷位置对频率改变的影响相对复杂，一些位置的缺陷对低频成分影响大，另一些位置的缺陷则对高频成分影响大。虽然用固有频率无法直接确定缺陷的位置，但可以用它来构造对位置敏感的缺陷识别指标。Cawley等(1979)认为结构含有缺陷时，仅引起结构刚度降低，而结构质量的变化可以忽略；他们还认为，缺陷引起的第i阶固有频率变化δω_i可以看作是刚度降低量δK及其缺陷位置矢量r的函数：

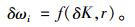
(5)

进一步分析证明，

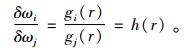
(6)

式中:仅是位置矢量r的函数。

这样就得到含有缺陷时任意2阶频率改变量之比仅是缺陷位置的函数，而与缺陷大小无关。通过上述分析，即可构造出ζ₁为孔洞位置识别指标，ζ₂为孔径大小识别指标:

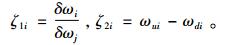
(7)

式中：ω_ui为完好试件的第i阶固有频率，ω_di为含孔洞试件的第i阶固有频率。

上述理论虽然是针对工程结构所建立的，但是本文中试件孔洞较小，孔洞对整个试件的质量影响也较小，主要影响因素仍然为试件的刚度变化，因此认为该理论同样适用于红松(Pinus koraiensis)试件缺陷检测。另外，参考文献(苏娟等, 1999; 万小朋等, 2003)中所建立的梁模型与本文中试件尺寸相仿，同样印证了该理论适用于尺寸较小的结构。

2 红松方材试件的模态试验 2.1 仪器和材料

试验设备采用日本A & D公司的AD-3651-02FFT分析仪，激振器为美国DYTRAN公司的应力锤5800B4，接收设备为DYTRAN公司的加速度传感器3035B。

采用红松树种作为研究对象，并将其制成110 cm×5.3 cm×5.3 cm的木材试件，试件总计15根，含水率均为9%。红松试件两端各留出5 cm，在中间的100 cm范围内以4 cm等距布置26个节点。把完好无缺陷试件作为标准试件，对其进行测试。然后，在其中5个试件的17，18节点间依次制出孔径为3，10，18，26，35 mm深20 mm的孔洞。对其余试件，在7，8节点间或13，14节点间制出直径为10 mm深为20 mm的孔洞，每种情况5个试件。节点和孔洞均布置在试件径切面上。

2.2 试验方法

利用力锤敲击，对红松试件进行振动试验模态分析。在试验过程中，为使红松试件处于一种近似的“自由状态”(李德葆等, 2001)，采用柔软的橡胶绳把红松试件悬挂起来。绳索悬挂在2，3节点之间和24，25节点之间。力锤采用橡胶锤头，加速度传感器安装在1号节点和试件端头中间位置。采用多点输入单点输出的方法对试件进行测试，用力锤从第1节点开始逐个敲击每个节点，对每个节点至少敲击5次取平均结果。

信号采集及分析处理采用与AD-3651-02FFT分析仪相配套的WCAPRO软件。采用两通道对信号进行采集，通道1为激励通道(连接力锤)，通道2为响应通道(连加速度传感器)，耦合方式为AC交流电耦合。信号采集过程中，采样点数为1 024，分析频段为800 Hz，采样频率为2 048 Hz。为了尽量消除无限序列截断引起的吉布斯效应和能量泄漏，分别对力函数和响应信号施加矩形力窗和高斯窗。

对采集到的信号进行分析，运用模态参数识别方法识别红松试件的固有频率，以固有频率构造缺陷识别指标，送入利用Matlab编制的神经网络程序进行识别。

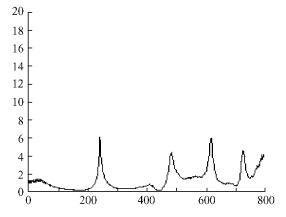
2.3 试验结果

1) 试验测得的频响函数    试验测得的信号经过WCAPRO软件的FFT分析，可生成随频率变化的曲线，即频响函数曲线。频响函数是频域模态参数识别的基本依据，因此通过模态试验首先需要得到能够准确反映试件振动特性的频响函数曲线(李德葆等, 2001)。图 1是通过振动测试得到的标准无孔洞试件的频响函数曲线。从图 1可以看出，红松试件各阶模态较为分散，因此宜采用单模态参数识别法对试件的固有频率进行识别。

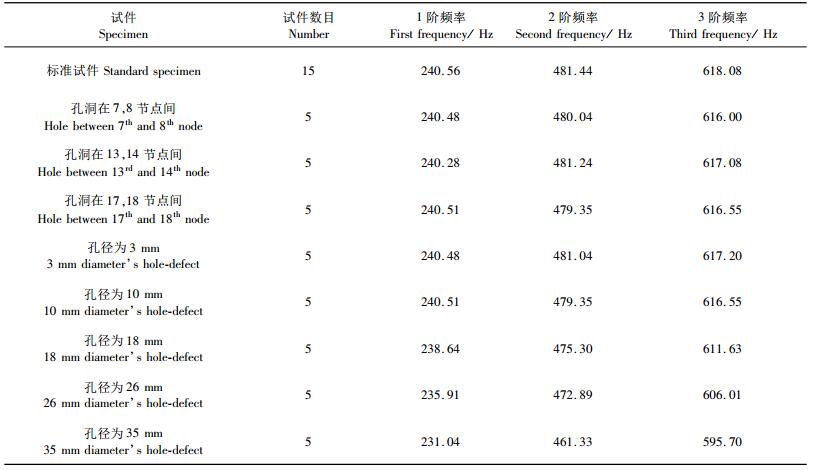
2) 固有频率识别    固有频率是通过模态试验最容易得到的模态参数，也是通过试验能够得到的较为准确的参数之一(李德葆等, 2001)。表 1为红松试件前3阶固有频率的平均值。从表 1中可以看出，含有孔洞的方材试件的前3阶固有频率与标准试件相比均有所下降。其中，在不同节点位置含有直径为10 mm深为20 mm孔洞的试件，其固有频率有所下降，但下降程度并不大，这主要是由于孔径较小的原因。然而，随着孔洞孔径的加大，在17，18节点间含有孔洞试件的固有频率下降程度也在逐渐加大。

3 BP神经网络设计

BP神经网络的设计主要包括输入层、隐含层、输出层及各层之间的传输函数几个方面(甘敬等, 2007; 琚存勇等, 2006)。本文采用典型的3层BP神经网络，即包含1个隐含层。

3.1 输入层设计

以试验模态分析得到的红松试件前3阶固有频率为原始数据，根据式(7)分别计算对孔洞位置和大小敏感的指标ζ₁和ζ₂。当对孔洞进行定位检测时，采用ζ₁₁，ζ₁₂，ζ₁₃作为输入参数，输入神经元设为3个。对含有不同位置孔洞的试件，各选取20个节点的数据进行训练，共计300(5×3×20)组训练数据。然后，对每个试件各选取一组未参与训练的数据测试网络的有效性，共计15组测试数据。

当对含有不同孔径试件进行定量检测时，采用ζ₂₁，ζ₂₂，ζ₂₃作为输入参数。同样，对每个试件选取20组数据进行训练，对应于不同孔径大小，共计500(5×5×20)组训练数据。训练结束后，对每种情况各选取3组数据进行测试，对应于5个孔径，共15组测试数据。

3.2 隐含层神经元及函数选取

BP网络中隐含层神经元一般设定为2L+1个，L为输入层神经元个数。另外，依据模型选取6，7，8，9，10等不同隐含层神经元个数时收敛性的对比结果，发现神经元个数为7时网络收敛速度最快，因此本文中隐含层神经元个数设定为7个。由于传输函数logsig的输出值在(0，1)之间，而purelin的输出为任意值，因此，进行孔洞定位识别时，输入层到隐含层的传输函数为tansig，隐含层到输出层选取logsig；进行孔径定量识别时，输入层到隐含层的传输函数为tansig，隐含层到输出层选取purelin。训练函数均选取trainlm，误差性能函数选取mse。

3.3 输出层设计

根据不同的目的，输出层神经元选取不同的个数。当进行孔洞定位识别时，输出层神经元设为3个，理想输出值分别为(0 0 1)，(0 1 0)，(1 0 0)，分别对应孔洞位置在7，8节点间，13，14节点间，17，18节点间。当进行孔径大小定量识别时，输出神经元设为1个，理想输出值为3，10，18，26，35，对应不同孔径大小。

4 红松试件孔洞缺陷识别 4.1 红松试件孔洞缺陷的定性识别

红松试件在不含孔洞和含有不同孔径孔洞时的频率变化如图 2所示。对图 2进行分析可以得到：1)红松试件在含有孔洞时固有频率将减小；2)固有频率对孔洞缺陷的敏感度各阶并不均等；3)缺陷引起的频率变化随孔径大小呈非线性增大, 即频率对大缺陷更敏感。因此，根据频率变化可以直观地判断红松试件是否含有孔洞。

4.2 红松试件孔洞缺陷的定位识别

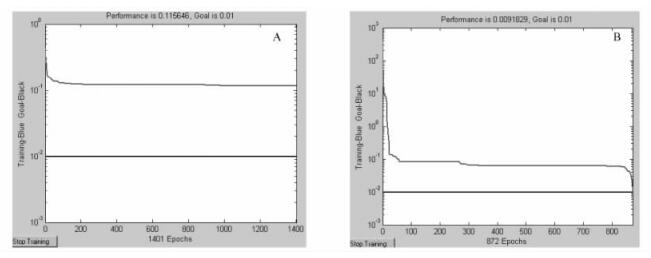
采用Matlab平台建立的缺陷定位识别神经网络对学习数据进行训练，训练结果见图 3A，终止时迭代1 401步，收敛精度0.115 6，误差目标0.01，在200步之后变化非常缓慢，故人为终止。利用训练后的网络对待测样本数据进行测试，测试结果如表 2。从表 2中可以清楚看到，实际输出值与理想输出值符合得非常好，这也正好表明利用任意2阶频率变化之比ζ₁作为参数能够对孔洞位置进行有效的识别。

4.3 红松试件孔径大小的定量识别

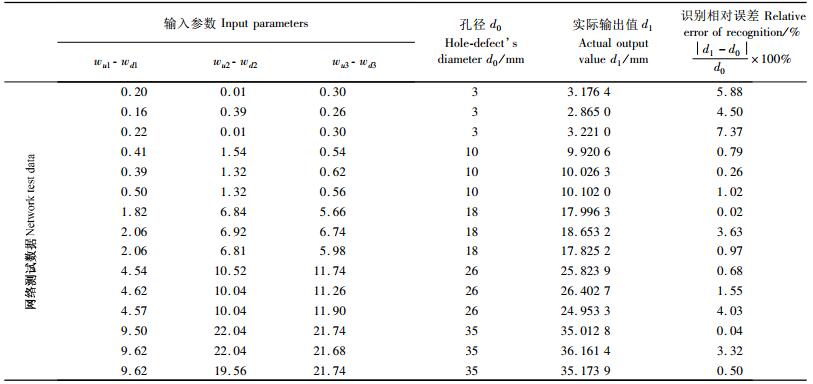
利用定量识别神经网络对学习样本进行训练，训练结果见图 3B，终止时迭代872步，收敛精度0.009 2，误差目标0.01，训练速度很快。同样，利用训练后的网络对待测样本数据进行测试，测试结果如表 3。从表 3可以清楚地看到，网络识别的相对误差最大为7.37%，最小仅为0.02%，从而表明可以运用频率变化ζ₂对红松试件的孔洞大小进行识别。表 3中数据还表明，定量识别神经网络对孔径10 cm以上的孔洞识别误差均在5%以下，而对孔径为3 cm的孔洞识别误差更大一些，表明网络对较大的孔洞缺陷识别更为准确一些。

5 结论

试验模态分析技术能够通过简便易行的振动法获取表征木材缺陷的模态参数，而BP神经网络则可以对模态参数数据进行有效的训练，从而依据模态参数的变化对缺陷进行识别，把二者结合起来应用将为木材无损检测提供一条新的思路。

从上述讨论可知，采用试验模态分析方法可以获取红松试件的频响函数，对频响函数进一步分析则能够得到红松试件的前3阶固有频率，根据固有频率的变化可以很直观的判断红松试件是否含有孔洞。利用固有频率构造的频率变化比ζ₁和频率变化ζ₂分别对孔洞位置和孔径大小具有较好的敏感度，并据此构造了定位识别神经网络和定量识别神经网络。通过神经网络对样本数据的训练和测试，表明构造的神经网络能够对孔洞位置和孔径大小进行有效的识别。