文章信息
- 赵春燕, 李际平, 李建军
- Zhao Chunyan, Li Jiping, Li Jianjun
- 基于Voronoi图和Delaunay三角网的林分空间结构量化分析
- Quantitative Analysis of Forest Stand Spatial Structure Based on Voronoi Diagram & Delaunay Triangulated Network
- 林业科学, 2010, 46(6): 78-84.
- Scientia Silvae Sinicae, 2010, 46(6): 78-84.
-
文章历史
- 收稿日期:2009-09-20
- 修回日期:2009-11-25
-
作者相关文章
与林木空间位置有关的结构称为林分空间结构。林分空间结构决定了树木之间的竞争优势及其空间生态位,在很大程度上影响着林分生长、发育和稳定性。按照森林经理的观点,空间结构可从3个方面加以描述:体现树种空间隔离程度的树种混交度(惠刚盈,2001);反映林木个体大小的大小比数(惠刚盈等,1999);反映林木个体在水平地面上分布格局的角尺度(惠刚盈等,1999)。混角度、大小比数和角尺度完全可以恰当地表征一个林分的空间结构(惠刚盈,1999)。在空间结构指数研究中,其最重要的参数即对象木的最近邻木株数n的取值尚有争议,n取值过大时,可能把非最近邻木也纳入计算范围;n取值过小不能兼顾对象木周围最近邻木的所有可能情形。这2种状况都将导致空间结构参数的有偏估计(汤孟平等,2009)。
Voronoi图是按照对象集合中元素的最近属性将空间划分成许多单元区域,是对空间的一种剖分方式,Voronoi图中任意一个凸多边形,任意一个内点到该凸多边形的控制点的距离小于该点到其他任何控制点的距离。Voronoi图具有最近性、邻接性的性质,利用Voronoi图这些性质为林分空间结构量化分析提供依据。汤孟平等(2009)在用混交度表达树种空间隔离程度时,用Voronoi图确定最近邻木株数n, 克服n取值过大或过小导致混交度偏估。在用大小比数表示林木个体大小时,同样可以利用Voronoi图确定最近邻木株数。在用角尺度表示林木个体在水平地面上分布格局时,利用Voronoi图的对偶结构Delaunay三角网,这种三角网具有最小角最大化原则,即每2个相邻的三角形构成凸四边形的对角线,在相互交换后,6个内角的最小角不再增大(Lawson,1977),这样可以最大程度地保持均衡, 避免狭长形三角形的出现,且Delaunay三角网中每个三角形边长对应相邻木之间的距离,这种结构能够较好反映水平地面的分布格局。本文在广东湛江红树林国家自然保护区选择样地进行试验,以单株木视为平面上的离散点,构建Delaunay三角网和Voronoi图,以此结构为依据确定每株对象木的最近邻木数和最近邻木,计算混交度、大小比数和角尺度,并把计算结果与最近邻木数取4的传统算法进行对比分析,以此探索使用计算几何中的数据结构分析林分空间结构的可行性和合理性。
1 林分空间结构指数 1.1 混交度混交度计算公式为(惠刚盈等,2001):
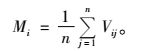
|
(1) |
式中:Mi为对象木i的混交度,n为最近邻木株数,Vij是一个离散性的变量,当对象木i与第j株相邻木非同种时, Vij=1,反之,Vij=0。显然,0≤Mi≤1。Mi=0表示参照树i的周围n株相邻木与参照树均属同一树种;Mi=1则表示参照树i的周围n株相邻木与参照树均属不同树种。混交度表明了任意一株树的最近相邻木为它种的概率。
1.2 大小比数大小比数被定义为大于参照树的相邻木数占所考察的全部最近相邻木的比例,用公式表示为(惠刚盈等,1999):
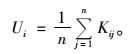
|
(2) |
式中:相邻木j比参照树i小,Kij=0;否则Kij=1。大小比数量化了参照树与其相邻木的关系,其值(Ui)越低,说明比参照树大的相邻木越少。
1.3 角尺度(wi)角尺度用来描述相邻树木围绕参照数i的均匀性。对参照树i的n个相邻最近树而言,均匀分布时其位置分布角应各为360°/n(惠刚盈,1999)。定义a0(a0=360°/n±360°/10 n)为标准角,角尺度(wi)定义为a角小于标准角a0的个数占所考察的相邻最近树的比例,用下式表示(惠刚盈,1999):
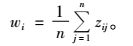
|
(3) |
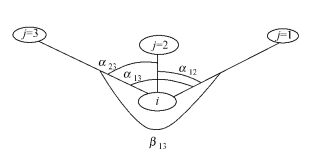
式中:当第j个a角小于标准角a0则zij=1,否则zij=0。0≤zij≤1,zij值越小,分布越均匀。角尺度示意如图 1。
|
图 1 角尺度示意 Figure 1 Schematic diagram of neighborhood pattern |
Voronoi图又叫泰森多边形,N个在平面上有区别的点,按照最邻近原则划分平面;每个点与它的最近邻区域相关联。点目标的二维Voronoi区域表示为(邬伦等,2001):
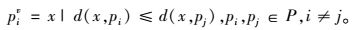
|
(4) |
式中:piv为目标点pi的Voronoi区域;x为空间任一点;d为平面距离函数。所有点目标的二维Voronoi区域的集合构成点集P的Voronoi图PV为:
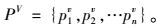
|
(5) |
PV把平面划分成n个多边形域,每个多边形域piv包含且只包含一个点pi。
Delaunay三角形是由与相邻Voronoi多边形共享1条边的相关点连接而成的三角形, Delaunay三角形的外接圆圆心是与三角形相关的Voronoi多边形的一个顶点。Voronoi三角形是Delaunay图的偶图, 对于给定的初始点集P,有多种三角网剖分方式,其中Delaunay三角网具有以下特征(许丽敏等,2009):1) Delaunay三角网是唯一的;2)三角网的外边界构建的多边形为群点凸壳;3)任意三角形的外接圆内不包含其他点;4)三角网最大程度地保持了均衡, 避免狭长形三角形的出现。
2.2 由树木点位置生成的Voronoi图和Delaunay三角网的特点在广东湛江红树林国家自然保护区,选择典型的红树林设置大小为100 m×100 m的样地,用相邻格子调查方法,把样地划分为25个20 m×20 m的调查单元。用全站仪测定每株树木的坐标,每株树木被视为平面上的一个点,根据每株树木的平面坐标位置,使用ArcGIS软件的构建Voronoi图和Delaunay三角网功能,首先由树木点位置构成的离散点生成三角网,这种三角网称之为Delaunay三角网(图 2),Voronoi图和Delaunay三角网互为对偶,由此建立的Voronoi图和Delaunay三角网具有以下特点:
|
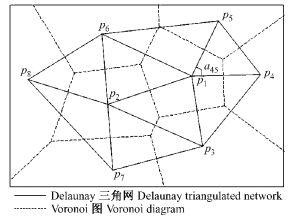
图 2 Voronoi图与Delaunay三角网 Figure 2 Voronoi diagram and Delaunay triangulated network |
1) 根据Voronoi图的特征,每个Voronoi多边形内仅包含1株树木,对象木的最近邻木株数与相邻Voronoi多边形边的数目相等,如图 2是由点集{p1, p2, p3, p4, p5, p6, p7, p8}构建的Voronoi图和Delaunay三角网,由p1构建的Voronoi多边形边的数目为5,则以p1为对象木的最近邻木株数为5,对应的最邻木为p2, p3, p4, p5, p6;
2) 对象木的最邻木数和以此相联接的Delaunay三角网个数相等,图 2中对象木p1与5个最近相邻木构成5个Delaunay三角网,依次为Δp1p2p3,Δp1p3p4,Δp1p4p5,Δp1p5p6和Δp1p6p2三角形;
3) 对象木与最近邻木的距离即为构建Delaunay三角网相对应的三角形边长,图 2中对象木p1与5个最近相邻木的距离为Delaunay三角网的边p1p2,p1p3,p1p4,p1p5和p1p6的边长;
4) 从对象木出发,任意2个最近相邻木的夹角即为对应Delaunay三角网2条边的夹角,图 2中对象木p1的最近相邻木p4p5的夹角即为a45。
3 实例分析 3.1 试验区概况本研究区位于广东湛江红树林国家自然保护区,109°40′—110°35′E, 20°14′—21°35′N,其红树面积占全国红树林面积的33%。其中以白骨壤(Avicennia marina)树种为优势的林分最多,其次为以红海榄(Rhizophora stylosa)和秋茄(Kandelia candel)为优势树种的2种林分。
根据林分空间结构理论和森林生态系统经营理论(惠刚盈等,2003;刘素青,2006)及红树林生长环境特殊性等特点,分析红树林保护区典型林分,确定每株林木的空间属性因子(李春干,2003),采用标准调查方法,对所选林分胸径大于2 cm的进行每木调查。
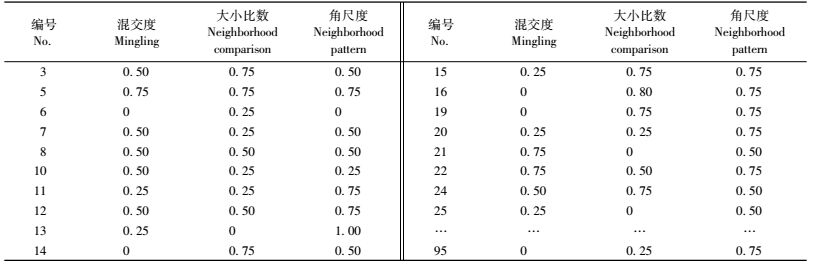
3.2 混交度、大小比数、角尺度计算其中一个调查样地范围内共有95株树木,除去周边26株树木,对象木共69株。计算混交度、大小比数和角尺度,首先取对象木的最近相邻木n为4,对调查区域内69株对象木进行每木调查,按照式(1)、式(2)和式(3)进行计算,其中大小比数以胸径为大小对比依据,得到结果如表 1(编号为图 3中对象木的编号)。
|
|
|
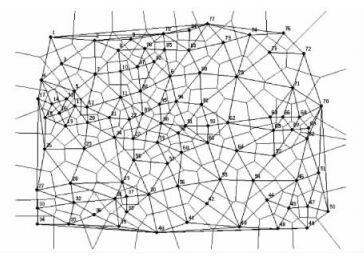
图 3 由试验区内对象木构建Voronoi图和Delaunay三角网 Figure 3 Voronoi diagram and Delaunay triangulated network of target tree from experimental areas |
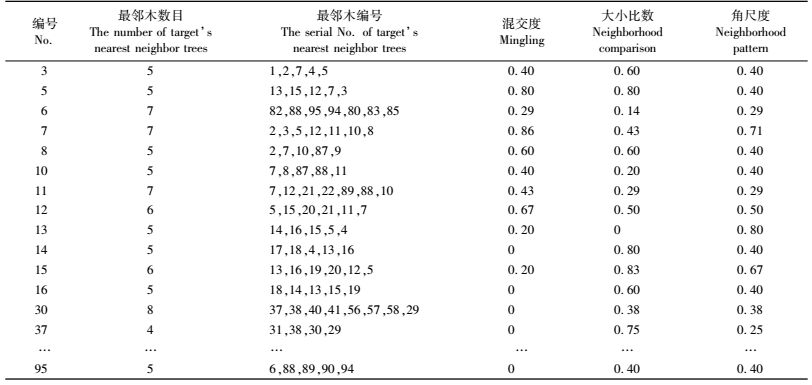
把每株树木视为平面上的一个点,根据每株树木的平面坐标位置,使用ArcGIS软件的构建Voronoi图和Delaunay三角网功能,由树木点位置生成Voronoi图和Delaunay三角网如图 3,根据Voronoi图确定参照木的最邻木数和最近邻木,计算空间结构指数的结果如表 2。
|
|
在研究区域范围内,共测试693株对象木,由树木点位置构建Voronoi图和Delaunay三角网,确定对象木的最近邻木数,由ArcGIS软件分析对象木与最近邻木的距离,计算林分个体的混交度、大小比数、角尺度,与最近邻木数取4计算的结果进行对比分析,能够得出:
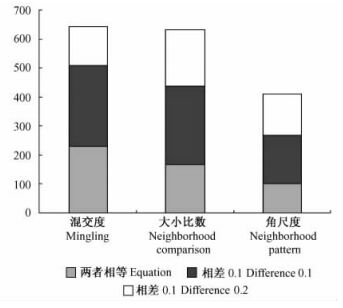
1) 基于Voronoi图和Delaunay三角网的混交度、大小比数和传统方法计算结果有较高的相关性和一致性趋势(图 4),均为有效指数,这与汤孟平等(2009)基于Voronoi图的常绿阔叶林混交度研究结果一致。对比2种计算方法,计算结果差异较小,混交度指数计算结果相等和相差0.1的共有509株,占总数的73.45%,相差0.2以上只有52株,占总数的7.5%。大小比指数计算结果相等和相差0.1的共有438株,占总数的63.2%,相差0.2以上的只有68株,占总数的9.81%。
|
图 4 基于Voronoi图和Delaunay三角网与传统空间结构指数计算结果对比 Figure 4 Calculation comparison of spatial structure indexes between based on Voronoi diagram and Delaunay triangulated network and traditional algorithms |
2)基于Voronoi图和Delaunay三角网的角尺度与传统方法计算结果差异较大(图 4),对比2种计算方法,角尺度指数计算结果相等和相差0.1的共有268株,占总数的38.67%。因为构建Voronoi图确定最近邻木时各个方向都有选取,任何一个Delaunay三角形具有最小角最大化原则,即每2个相邻的三角形构成凸四边形的对角线,在相互交换后,6个内角的最小角不再增大(Lawson,1977)。因此,角尺度的取值均小于传统计算方法。Delaunay三角网属于计算几何中空间特征描述结构,此结构本身反映个体在水平地面的分布格局。
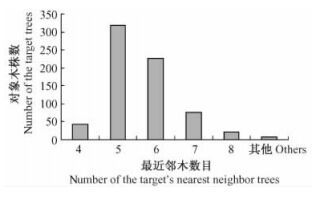
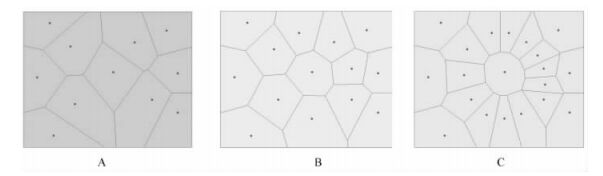
3) 通过Voronoi图和Delaunay三角网的相邻多边形确定对象木的实际最近邻木,比传统方法更准确地描述种间相互隔离关系和个体大小比。主要因为传统方法计算结果取值只有0,0.25,0.50,0.75,1,缺少中间状态。而基于Voronoi图和Delaunay三角网的取值与每个对象木的最近邻木数有关,试验中,最近邻木数取值5和6较多,平均取值为5(图 5)。汤孟平等(2009)基于Voronoi图的常绿阔叶林混交度研究中平均取值为6,最近邻木数取值与林木个体在水平地面的空间分布有关,图 6中不同空间分布的最近邻木数取值不同,图 6A中对象木周围有4株最近邻木,图 6C中对象木周围有13株最近邻木。Voronoi图实际上是反映林木之间的空间竞争的结果,在天然林中反映对象木与临近木之间对阳光、水分、养分等环境的竞争结果。
|
图 5 最近邻木数的分布 Figure 5 Nearest neighbor trees number distribution |
|
图 6 最近邻木数不同取值的对比 Figure 6 Comparison of different values of the nearest neighbor tree number A.最近邻木数为4 The number of the nearest neighbor trees is 4;B.最近邻木数为7 The number of the nearest neighbor trees is 7;C.最近邻木数为13 The number of the nearest neighbor trees is 13. |
1) Voronoi图为林分确定参照木的最邻木数提供灵活性,林分内任意一株单株木和离它最近的n株相邻木均可以构成林分空间结构的基本单位,即林分空间结构单元。空间结构单元核心的那株树被称为参照树,而最近的n株相邻树木则称为相邻木。最邻木数目影响林分的大小比数、混交度、角尺度的值,一般取n为4的较多; 但是在一个研究区域内,不同样地内或同一样地不同空间位置林分空间结构不同,基于Voronoi图确定最邻木数及最近邻木往往更能反映实际的空间结构,如图 6C中,基于Voronoi图确定最近邻木为13,与对象木距离相差不大的临近范围内有13株林木,按照最近邻木取4的方法,不同样地调查人员所取最近邻木可能不同,影响空间结构指数计算结果。
2) Delaunay三角网为对象木确定最近邻木提供技术支持,根据Delaunay三角网性质,每个三角形的外接圆范围内没有其他节点,任何一个Delaunay三角形具有最小角最大化规则(许丽敏等,2009),三角形的每一条边是连接相对应方向最邻近2个节点,以此可以确定最近邻木。
3) Delaunay三角网中三角形边长即为对应参照木与最邻木之间距离,任意2个最近相邻木的夹角即为对应Delaunay三角网2条边的夹角,因此,样地调查时不需要参照木与最邻木之间距离和角度量算。Voronoi图和Delaunay三角网构建使用ArcGIS软件实现,此结构中边长和角度的计算可以通过计算机程序实现。
4.2 空间分布格局对空间结构指数技术的影响由单株木为平面点构建Voronoi图和Delaunay三角网,确定对象木的最近邻木时,对象木与最近邻木的距离最近为23 cm,距离最远为330 cm,差异较大。在实际分析中,距离较远的往往不作为最近邻木考虑,因此,对这种情况需要分析处理。对象木与最近邻木的距离与空间分布格局有关,林木个体的空间分布格局是指林木个体在水平空间的分布状况。林木空间分布格局类型基本有3种:随机分布,每个个体的出现具有同等的机会,个体的分布相互间没有联系,林木以连续而均匀的概率在林地上分布;均匀分布,林木在水平空间均匀等距地分布,或者说林木对其最近相邻木以尽可能最大的距离均匀地分布在林地上,林木之间互相排斥;聚集分布,林木之间互相吸引,具有相对较高的超平均密度占据的范围。
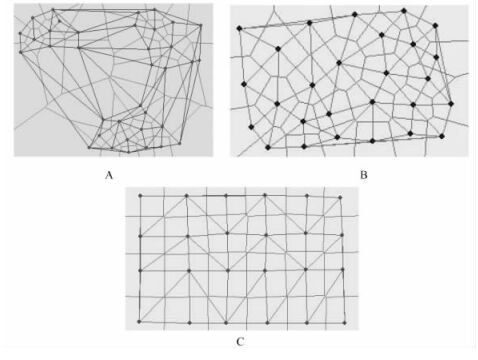
3种空间分布格局情况下构建的Voronoi图和Delaunay三角网(图 7),以均匀分布的林木构建的Voronoi图的多边形呈现一定规则性,每个Voronoi图的多边形是近四边形,每个对象木的最近邻木数取值范围为4~8,其对应Voronoi图为四边形至八边形,但是每个多边形中有4条边的边长相对较长,其余边长较短。聚集分布的林木呈簇状,以聚集分布林木构建的Voronoi图,簇内Delaunay三角网的边长较短,簇间Delaunay三角网边长较长,只把聚集在一团内的林木作为最邻木考虑,在Delaunay三角网内边长大于一定阈值的三角形边不考虑在内。
|
图 7 不同空间分布形式的Voronoi图和Delaunay三角网 Figure 7 The Voronoi diagram and Delaunay triangulated network with different spatial distribution forms A.聚集分布Aggregated distribution;B.随机分布Random distribution;C.均匀分布Uniform distribution. |
本文利用ArcGIS的空间分析功能,以林分中单株木视为平面点构建的Voronoi图和Delaunay三角网能够为林分空间结构研究提供技术支持,以此为基础确定对象木的最近邻木更加灵活、合理,在此基础上计算的混交度、大小比数能反映实际空间结构特征,而Voronoi图是对空间的一种剖分,Voronoi图的构图形式本身反映林木空间分布格局。通过分析Voronoi图的结构特征,来剖析林木空间分布格局将成为后续研究,以此探索使用计算几何中的数据结构分析林分空间结构的合理性和有效性,并在此基础上挖掘GIS中空间数据结构在林分空间结构量化分析。
冯仲科, 郭清文, 朱萍. 2006. Voronoi图-泰森多边形法在角规测树中的应用[J]. 林业资源管理, (3): 44-47. |
惠刚盈, Klausvon Gadow, MatthiasAlbert. 1999. 一个新的林分空间结构参数——大小比数[J]. 林业科学研究, 12(1): 1-6. |
惠刚盈, 胡艳波, 徐海. 2005. 森林空间结构的量化分析方法[J]. 东北林业大学学报, 33(增): 45-48. |
惠刚盈, 胡艳波. 2001. 混交林树种空间隔离程度表达方式的研究[J]. 林业科学研究, 14(1): 23-27. |
惠刚盈, 胡艳波. 2006. 角尺度在林分空间结构调整中的应用[J]. 林业资源管理, (2): 31-35. |
惠刚盈, 冯佳多. 2003. 森林空间结构量化分析方法[M]. 北京: 中国科学技术出版.
|
惠刚盈. 1999. 角尺度——一个描述林木个体分布格局的结构参数[J]. 林业科学, 35(1): 37-42. |
雷相东, 唐守正. 2002. 林分结构多样性指标研究综述[J]. 林业科学, 38(3): 140-146. DOI:10.11707/j.1001-7488.20020325 |
李春干. 2003. 广西红树林资源的分布特点和林分结构特征[J]. 南京林业大学学报:自然科学版, 27(5): 15-19. |
刘彦, 余新晓, 岳永杰, 等. 2009. 北京密云水库集水区刺槐人工林空间结构分析[J]. 北京林业大学学报, 31(5): 25-28. |
刘素青. 2006. 森林生态系统经营与自适应模型研究. 中南林业科技大学博士学位论文.
|
汤孟平, 唐守正, 雷相东. 2004. 两种混交度的比较分析[J]. 林业资源管理, (4): 25-27. |
汤孟平, 周国模, 陈永刚, 等. 2009. 基于voronoi图的天目山常绿阔叶林混角度[J]. 林业科学, 45(6): 1-5. DOI:10.11707/j.1001-7488.20090601 |
邬伦, 刘瑜, 张晶, 等. 2001. 地理信息系统——原理、方法和应用[M]. 北京: 科学出版社.
|
许丽敏, 薛安. 2009. 基于Delaunay三角网与Voronoi图联合提取等高线骨架的地形重建算法研究[J]. 北京大学学报:自然科学版, 45(4): 647-652. |
Lawson C I. 1977. Software for C surface interpolation//Rice J R.Mathematical Software Ⅲ.New York: Academic Press, 161-194.
|
 2010, Vol. 46
2010, Vol. 46