红树林生态系统是处于海洋生态系统与陆地生态系统之间经长期演替形成的一种系统结构稳定、生产力高的特殊森林生态系统，可看做一种顶极群落景观，在生物多样性与减灾防灾功能上具有不可替代的作用(韩维栋等, 2009)。在保护和恢复红树林中，如何重构林分空间结构，恢复红树林的功能，发挥其系统功能和减灾防灾效用成为当前迫切需要解决的问题。林分空间结构是从单木的角度表达林分在某一时刻的空间信息，决定了林木之间的竞争势及其空间生态位, 从而很大程度上决定了林分的稳定性。林分空间结构理论的主要研究内容为在空间上优化和调整林分内的林木分布，建立林木的空间因子指标体系(Mark et al., 1998.)。而如何确定林分的空间结构优化目标、合理选择其影响因子，同样是天然林生态系统恢复和经营研究的焦点(汤孟平等，2004)，在此背景下，研究红树林生态系统空间结构优化目标、建立其影响因子指标体系具有重要的理论意义和实践意义。

景观生态学的景观、斑块理论中，斑块内部要求均质且与邻近斑块有着本质不同的特征(Weintraub et al., 1991)，近年来国内外学者在研究天然林次生林生态采伐时把林分作为空间结构研究的基本单位，将斑块均质性理解为林分空间结构的均质性(张会儒等，2006)。景观生态学理论和国内外天然林空间结构已有的研究成果，为明确红树林生态系统空间结构优化目标、量化指标参数及建立空间结构指标体系提供了参考和理论依据。本研究提出红树林林分空间结构优化目标及描述红树林林分内各单株林木空间结构特征的量化指标—均质性指数，并应用灰色关联度分析法研究广东湛江红树林国家自然保护区不同潮带林分空间结构因子与均质性指数的关联程度。

1 研究区概况

研究区位于广东湛江红树林国家自然保护区(109°40′—110°35′E, 20°14′—21°35′N)，其红树林面积占全国红树林面积的33%。红树林中以白骨壤(Avicennia marina)为优势种的林分最多，其次为以红海榄(Rhizophora stylosa)和秋茄(Kandelia candel)为优势树种的林分。广东湛江廉江市高桥红树林保护区，属于受过干扰后有所恢复的天然红树混交林，该保护区始建于1991年7月, 地处广东、广西交界的北部湾英罗港, 东侧为卖皂海, 西侧为官寨海。1997年12月经国务院批准, 由省级自然保护区晋升为国家级自然保护区。全保护区总面积1.3万hm², 是我国最大的红树林自然保护区。主要保护对象是红树林、鸟类及其栖息地、浅海生物资源等。区内有珍贵红树林树种24种，鱼类127种，贝类110种，鸟类190多种。2002年保护区加入拉姆萨公约，成为国际重要湿地。

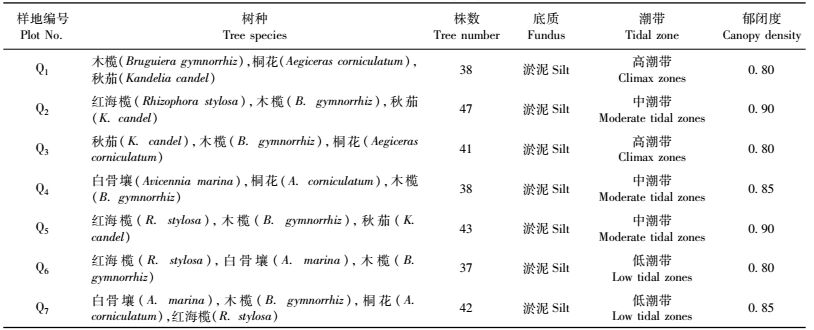
2 数据来源

根据林分空间结构理论和森林生态系统经营理论(惠刚盈等，2003; 刘素青，2006)和红树林生长环境特殊性等特点，分析红树林保护区典型林分，按照研究数据调查要求，选择7个具有代表性的典型地段设立标准样地7块, 分别编号为Q₁, Q₂, Q₃, Q₄, Q₅, Q₆和Q₇，样地概况见表 1。样地面积为10 m×10 m, 样地起测径级为3 cm。对每个样地进行每木调查，调查内容包括调查木和周围4株最近邻近木的树种、胸径、树高、枝下高、冠幅、目的树种特性指数、健康指数、角尺度、树种多样性指数(混交度)和大小比数10个指标以及调查木与4株相邻木的距离(刘素青，2006; 惠刚盈等，2007; 李建军等，2008)。

3 林分空间结构均质性指数 3.1 均质性指数的参数

林分内林木均质性指数定义的关键问题是合理选择反映红树林特征的参数和影响因子。林分空间结构包括混交、竞争和林木空间分布格局3方面(惠刚盈等，2001; 雷相东等，2002)，根据林分空间结构从单株林木的角度表达林分在某一时刻的空间信息的特点，结合红树林生态系统的特殊性，研究红树林林分均质性指数从林分内单株林木的树种特性、生长状况、混交、竞争和林木空间分布格局5方面选择参数。

1) 树种特性方面的均质性反映林木是否为顶极群落景观树种，当地顶极群落景观是长期演替形成的一种系统结构稳定、生产力高的森林生态系统，是森林生态系统经营的目标群落景观，用目的树种特性指数反映顶极群落景观树种关系(Hof et al., 2000; 刘素青，2006)。根据群落演替形成过程的树种组成特点，目的树种特性分成5种类型(刘素青，2006):①顶极群组成树种，A_i=1;②过度性群落树种，A_i=0.75;③先锋群树种，A_i=0.5;④非乡土树种，A_i=0.25;⑤入侵树种，A_i=0(A_i为第i株林木的目的树种特性指数)。

2) 根据古树群古树植株生长情况按标准将每株红树生长势分级，确定林木的生长情况(韩维栋等，2009)，林分在生长状况方面的均质性是不同林木与周围树木相比所处的健康地位，用健康指数H_i(刘素青，2006)描述林木的生长状况。健康指数是近自然经营单木营林技术的一个操作标准(刘素青，2006; 韩维栋等，2009)。

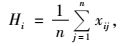
(1)

式中: x_ij为健康指数变量，属于2点变量, 当参照树i比邻近木j的健康状况差，x_ij=0，否则x_ij=1; n为邻近木株树。当邻近树木取4株进行观察时，健康指数H_i可能取值为:①H_i=0，参照树的健康差于相邻的4株树木; ②H_i=0.25，参照树的健康差于相邻的3株树木; ③H_i=0.5，参照树的健康差于相邻的2株树木; ④H_i=0.75，参照树的健康差于相邻的1株树木; ⑤H_i=1，参照树的健康与相邻的4株树木一致。

3) 林分在混交方面的均质性是不同树种林木之间充分隔离，混交林中树种相互隔离程度越高，林分稳定性越高(张会儒等，2006)，均质性指数在混交方面从树种和大小分化2方面考虑选择树种多样性指数M_i(惠刚盈，2003等; 刘素青，2006)(以下简称混交度)和大小比数U_i(惠刚盈等，2003)作为混交均质性量化参数。多样性指数(混交度)(刘素青，2006)用来说明混交林中树种空间隔离的程度。它被定义为参照树i的n株最近相邻木中与参照树不属同种的个体所占的比例，用公式表示为:

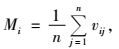
(2)

式中: M_i为林木i点混交度; v_ij是一个离散型的变量，当参照树i与第j株相邻木非同种时v_ij=1，反之，v_ij=0。大小比数(u_i)(惠刚盈等，1999)被定义为大于参照树的相邻木数占所考察的全部最近相邻木的比例，公式表示为:

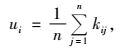
(3)

式中:u_i为大小比数, u_i值越小，说明该树种在某一比较指标(胸径、树高或树冠等)上越优先，依u_i值大小升序排列即可表明林分中所有树种在某一比较指标上的优劣程度; k_ij为离散变量，若参照树i比邻近树j小，k_ij=1，若参照树i比邻近树j大，k_ij=0。

4) 竞争指标通常分为2种:一种与距离有关, 一种与距离无关。按照既要考虑理论上的合理性又要兼顾实践的可行性的原则，选择与距离有关的竞争指标, 采用Hegyi(1974)提出的竞争指数模型:

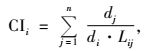
(4)

式中:CI_i为林木i的点竞争指数; L_ij为对象木i与竞争木j之间的距离; d_i是对象木i的胸径; d_j为竞争木j的胸径。

5) 林分在空间分布格局的均质性是林木均匀分布，天然林空间分布格局总的趋势是均匀分布(张会儒2006)，考虑林木在水平距离、角度和分布密度几方面选择均质性的指标参数，采用与树木分布状况和距离相关的角尺度W_i及空间密度指数D_i(惠刚盈等，2003; 刘素青，2006; 安慧君，2003)确定林木空间分布格局均质性的量化指标。角尺度(W_i)是反映树木分布状况的一种空间指标，它用来描述相邻树木围绕参照树i的均匀性。用下式来表示:

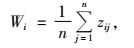
(5)

式中:W_i为角尺度; z_ij为角尺度取值变量，它是离散型的，z_ij=1。空间密度指数D_i反映林木空间分布密度的指标。其公式为:

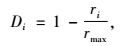
(6)

式中:r_i为参照树i包含相邻n株树木时的最小半径; r_max为林分中相邻2株林木的最大距离。

3.2 均质性指数的计算

综合林分空间结构树种特性、生长状况、混交、竞争、林木空间分布格局5个方面的分析，为使林木均质性指数能客观地描述林分内林木均质性，最大发挥影响林分空间结构均质性多方面的作用，研究采用乘除法(钱颂迪，1990)对各被选指标进行多目标规划，根据乘除法的基本思想，x是决策向量，当在m个目标f(x₁), …, f(x_m)中，有k个f(x₁), …, f(x_k)要求实现最大，其余f(x_k+1), …, f(x_m)要求实现最小，同时有f(x₁), …, f(x_m)>0，采用评价函数:

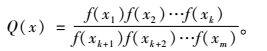
(7)

根据乘除法的基本思想, 对林分空间结构5个方面的均质性要求为:目的树种特性指数、健康指数、树种多样性指数(混交度)和大小比数以取大为优，而竞争指数、角尺度、和空间密度指数是取小为优。按公式(7)对林分空间结构均质性指标的5个子目标进行综合，确定林木均质性指数的计算公式如下:

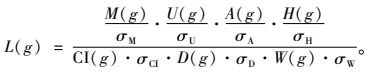
(8)

式中:L(g)为单木均质性指数; M(g)为混交度，σ_M为混交度标准差; U(g)为大小比数, σ_U为大小比数标准差; A(g)为目的树种特性指数，σ_A为目的树种特性指数标准差; H(g)为健康指数, σ_H为健康指数标准差; CI(g)为单木竞争指数, σ_CI为竞争指数标准差; D(g)为空间密度指数, σ_D为空间密度指数标准差; W(g)为角尺度，σ_W为角尺度标准差; g=(g₁, g₂, …, g_n)。

利用公式(8)对红树林林分进行数据处理时，由于混交度M、角尺度W等作为乘数因子都会有0数据出现，难以直接进行比较，故需要对公式(8)进行变换，根据乘除法的特点，将公式(8)各参数加1，得到公式(9)。林木均质性指标反映和衡量的林木与林分均质性目标不变。

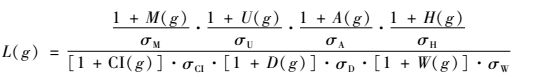
(9)

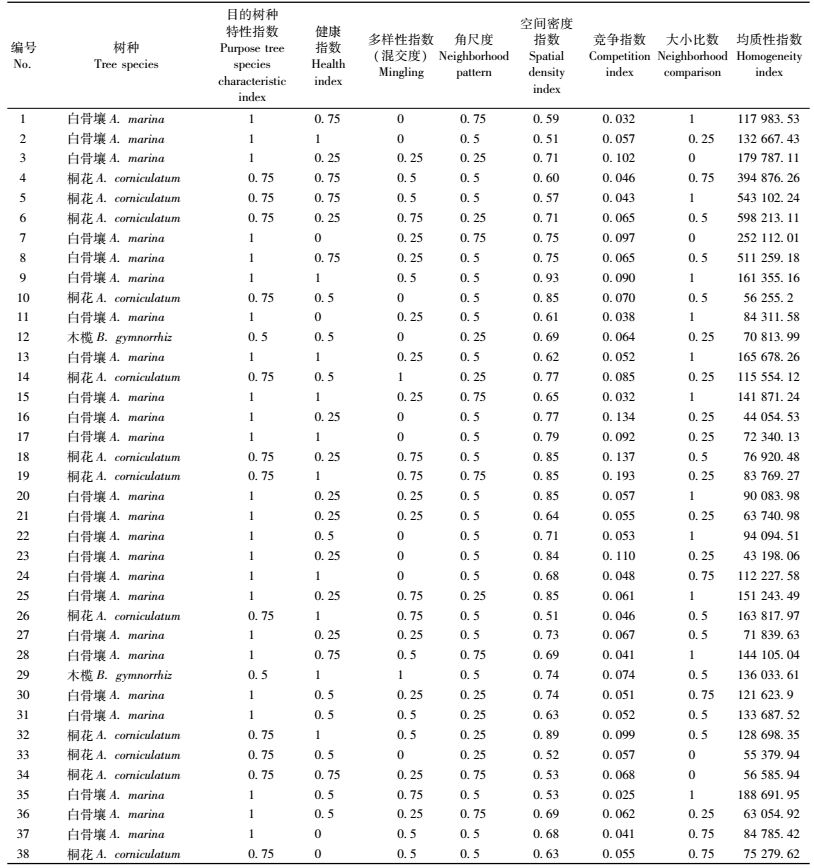
根据每木调查数据及公式(1—6)(惠刚盈等，2003; 刘素青，2006; 张会儒等，2006)和公式(9)计算出样地Q₃各林木均质性指数(表 2)。

4 均质性指数与其参数的灰色关联度分析

灰色关联法是灰色理论中一种常用的灰色系统分析方法，灰色系统是指部分信息明确、部分信息不明确的贫信息、不确定性系统(邓聚龙，2002)，灰色关联分析是灰色理论中的一种分析方法, 这种方法的基本思想是根据所研究的因子间变化的相似程度来判断关联程度，近年来在军事、农作物新品种选育及评价中得到广泛应用。红树林生态系统林分空间结构就可以看作是一个灰色系统。对于灰色系统，可以利用小样本数据建模，依据信息覆盖，通过序列生成寻求系统本身存在的规律。灰色关联分析的基本思想就是，根据序列曲线几何形状的相似程度来判断其联系是否紧密，曲线越相似，相应序列之间的关联度就越大，反之就越小。该方法既可以用于因素间关联度的分析，又可以用来对由多层次综合指标体系所描述的总体的优劣程度做出评判(黄振瑞等，2007)。

按照灰色关联度分析的要求，将林木均质性指数及其7个参数和样地38株红树林林木视为一个灰色系统。以林木均质性指数为参考数列X₀，目的树种特性指数、健康指数、多样性指数(混交度)、角尺度、空间密度指数、竞争指数和大小比数7个参数分别作为被比较数列X_i, i=1, 2, …, n，且X₀=[X₀(1), X₀(2), X₀(3), …, X₀(k)]，X_i=[X_i(1), X_i(2), X_i(3), …, X_i(k)]，n为参试林分内红树林起测林木株数，k为参试系数，(本研究中n=38，k=7)则其关联系数ε_i(k)如公式(10):

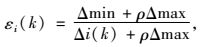
(10)

式中: Δi(k)=|X₀(k)-X_i(k)|为X₀数列与X_i数列在第k点的绝对差值; 在所有绝对差值中，Δmin和Δmax分别表示所有比较序列各个时刻绝对差中的最小值和最大值; ρ称为分辨系数，其意义是削弱最大绝对差数值太大引起的失真，提高关联系数之间的差异显著性，取值[ 0，1]，通常取ρ=0.5。由于关联系数数目较多，为了避免信息过于分散，便于比较，将各因子同等重要计算等权关联度r_i，即得到公式(11):

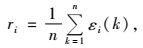
(11)

由r_i依大小排成的数列为关联序列，根据排序位次确定各影响因子对林木均质性指数的的影响程度(唐启义等，2002)。

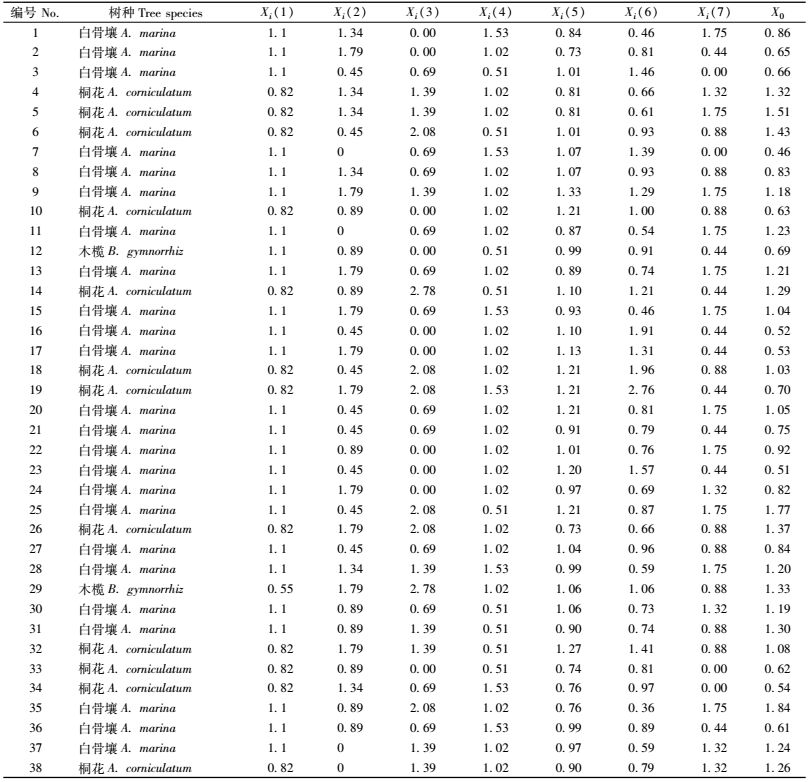
在表 2中，由于各参数原始数据量纲不同，难以直接进行比较，故需要对原始数据进行无量纲化处理，即以各性状的平均值去除该因子所有数据，得到一个新的数据列，所得具体数据见表 3。

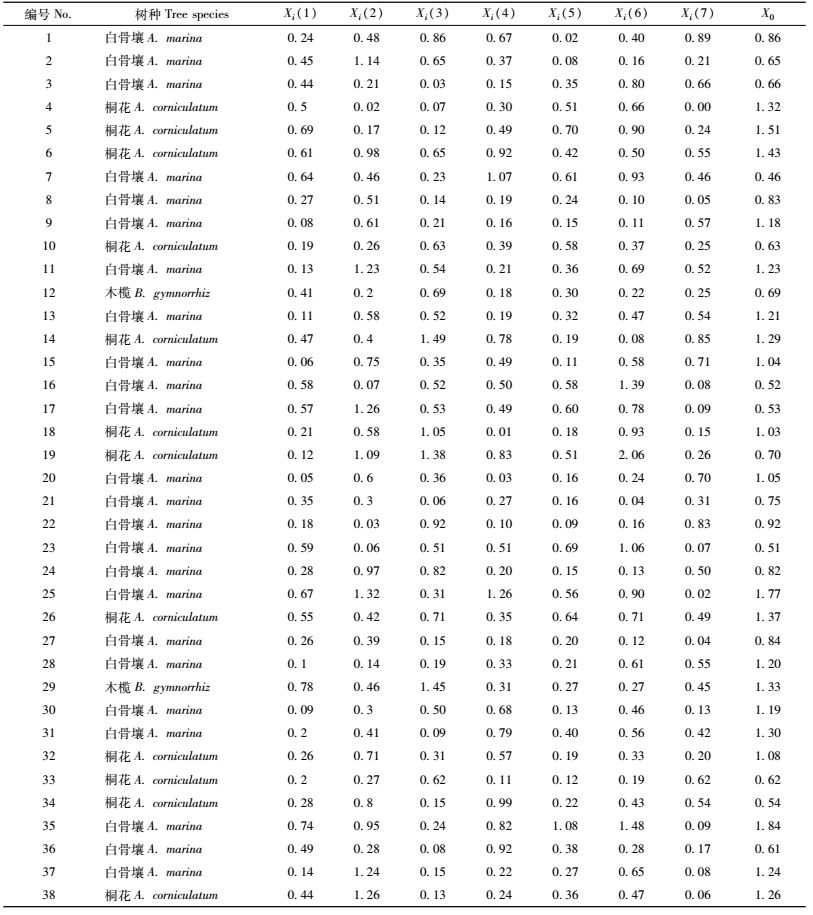
根据无量纲处理所得到的数据(表 3)，求得各参数与林分空间结构均质性指数的绝对差值，即Δi(k)=|X₀(k)-X_i(k)|，数据见表 4。

从表 4得到各因子的最小差值Δmin为0和最大差值Δmax为3.39，将ΔminX_i(k)和ΔmaxX_i(k)的值代入(10)式，并取系数ρ=0.5，即得到各主要影响因子与林木均质性指数之间的关联系数计算公式(12)式:

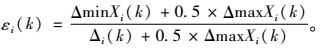
(12)

把表 4中相对应的数值代入(11)式即可得到各参数与林木均质性指数之间的关联系数ε_i(k)(表 5)。由于关联系数只反映2个被比较序列在某一时刻的紧密程度, 因此关联度取2个比较序列在各个时刻的关联系数的平均值(邓聚龙，2002)。

将求得的关联系数值代入公式(12)式，得到红树林林分空间结构均质性指数与混交度、角尺度、空间密度指数、竞争指数和大小比数等7个参数的关联度分别为0.644，0.607，0.686，0.638，0.670，0.716和0.616，关联度大小见表 5(黄振瑞等，2007)。

由表 5得知, 湛江红树林保护区不同潮带林分空间结构各均质性指数参数与均质性指数的关联度大小表现为竞争指数>多样性指数(混交度)>空间密度指数>目的树种特性指数>角尺度>大小比>健康指数。

应用同样的方法研究另外6个调查样地，所得结果与上述结果基本一致，各参数与均质性指数关联度排序不变，关联度大小误差未超过5%。说明研究结果较为真实。

5 结论与讨论

本研究通过借鉴国内天然林林分空间结构已有的研究成果，应用景观生态学理论，首次尝试提出优化林分空间结构均质性目标，创新了林分空间结构优化目标，同时提出了林分空间结构林木均质性指数的新概念。并使用多目标规划方法中的乘除法将影响林分空间结构均质性的树种特性指数、健康指数、竞争指数、多样性指数、空间密度指数、角尺度和大小比数7个参数进行目标归一，获得了林木均质性指数的定义和计算公式，为优化红树林林分空间结构提供了重要的理论数据。还在天然红树林中首次尝试使用了灰色关联度分析法对广东湛江红树林国家自然保护区不同潮带林分空间结构影响因子与林木均质性指数的关联度进行了分析，获得各影响因子与均质性指数的关联度大小:竞争指数0.716>混交度0.686>空间密度指数0.670>目的树种特性指数0.644>角尺度0.638 >大小比数0.616>健康指数0.607。

林分空间结构均质性指数能较客观真实地描述林木对林分空间结构的影响，同时以均质性为目标优化红树林空间结构不失为一种良好的选择。根据各参数与均质性指数的相关度大小，在红树林空间结构优化时应考虑多样性、竞争和水平均匀分布等相关指标。

本研究关联度检验时使用的参数和树木株数并不多，故用于分析的数据样本也不多，而样本数越多，关联度值越精确，越能更客观全面反映指标参数的真实性和实用行。

不同地带具有不同的森林类型，红树林林分空间结构均质性指标体系中的某些指标可能不具有普适性，因此在应用过程中可作相应的调整; 同时林分空间结构影响因子的评价十分复杂，难以完全量化，在实际操作过程中尊重专家的经验和知识仍然是十分重要的。