可燃物含水率预测是森林火险天气预报的重要内容，也是做好火险天气预报和火行为预报的关键(Anderson, 1964; 郑焕能等, 1992；邸雪颖, 1993; 王瑞军等, 1997; 胡海清, 2005; Rothermel et al., 1986; 何忠秋等, 1996; Nelson, 2000; Chuvieco et al., 2004)。基于时滞和平衡含水率预测可燃物含水率是目前最经典的方法(金森等，1999；2000；刘曦等，2007)。在该方法中，准确估计可燃物的时滞和平衡含水率十分重要。由于传统估测方法的复杂性，Catchpole等(2001)提出了利用野外数据直接估测可燃物含水率的方法(以下称“直接估计法”)(王会研等，2008)。该方法基于一种半物理平衡含水率模型，用初始含水率和环境中温、湿度值对可燃物含水率变化进行预测，方便快捷。

Catchpole等(2001)的直接估计法效果固然很好，可燃物含水率预测误差在2%以内，但该方法的有效性还没有得到全面的分析:一是方法的验证问题，又细化为2个子问题：1)建模数据和验证数据相同，自然提高了模型的准确率。如果采用不同于建模数据的验证数据，模型的准确率如何目前尚不清楚; 2)建模样本数对参数估计和预测结果的影响尚不清楚。这2个问题可合在一起研究。二是其他平衡含水率对温湿度的响应函数对方法的影响还没有研究。平衡含水率对温湿度的响应函数的选择是该方法的重要内容(详见1.1)。目前存在4种平衡含水率对温湿度的响应模型(Viney, 1991；刘曦等, 2007)：Simard(1968)模型、Van Wagner(1972)模型、Anderson等(1978)模型、Nelson(1984)模型。该方法采用Nelson模型。采用其他平衡含水率响应模型对该方法有何影响，目前也不清楚。这些问题不解决，会影响该方法的应用，无法判断根据该方法得到的结果的误差。为此，本文对直接估计法的有效性进行分析。

1 研究方法 1.1 时滞和平衡含水率直接估计法介绍

可燃物含水率随时间的变化可用下列方程描述：

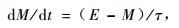
(1)

式中，M为可燃物含水率，%；E为平衡含水率，%；t为时间，h；τ为时滞，h。

假定时滞不随时间变化，可将方程(1)离散表达为：

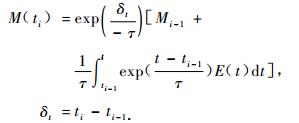
(2)

式中，M(t_i)为t_i时刻的含水率实测值，%; M_i-1为t_i-1时刻的含水率实测值，%; δ_t为野外采样时间间隔，h; E(t)为平衡含水率与时间的函数，单位时间间隔内为定值，%。平衡含水率与环境因子的关系采用Nelson模型：

(3)

式中，T为温度，K；H为湿度，%；R为普适气体常量，取8.314 J·K^-1mol^-1；M为H₂O的相对分子质量，18；a, b为待估参数。将(3)代入方程(2)得到：

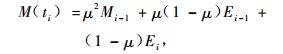
(4)

式中，E_i-1为t_i-1时刻的平衡含水率值，%; E_i为t_i时刻的平衡含水率值，%。

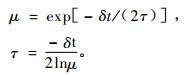
(5)

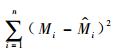
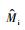
以误差平方和SSE=为目标函数，按目标函数值最小为约束做非线性估计，估计出μ和E中所含平衡含水率响应函数的参数(对于Nelson模型，为a, b)。其中M_i为实测含水率，%; 为预测含水率，%; n为样本数量。

1.2 可燃物含水率动态变化的测定

2008年3月在东北林业大学实验林场采集兴安落叶松(Larix gmelinii)枯枝(长度5 cm，直径分别为0.5, 1.0, 和1.5 cm, 以下简称D_0.5, D_1.0, D_1.5)，每种尺寸样品取10个重复，共30个样品。所有枯枝均未腐烂。在实验室内，1)按直径由小到大依次为30个样品编号。2)将可燃物放入105 ℃的烘干箱中连续烘干约8 h至恒质量，用电子天平分别记录每个样品的绝干质量(g)。3)将试验样品完全浸泡在水中1 h。4)将浸泡后的样品从水中取出，沥去表面水分，在空气中放置至表面无水。5)每40 min称取试验样品质量，同步测定温度、湿度，每天重复15次。6)每进行完1天试验后，重复步骤3), 4), 5), 共进行15天。

1.3 数据分析

由于平衡含水率响应模型可能对结果有影响，因此，在方法的验证上就要考虑不同的平衡含水率模型。在现有的4种平衡含水率模型中，Simard模型是美国国家火险等级系统中采用的模型，研究表明(刘曦等, 2007)，该模型拟合效果要比Nelson模型效果好，而其他2种模型的预测效果都不如Simard模型和Nelson模型。因此，在研究平衡含水率响应模型对方法效果的影响时，只采用Simard模型和Nelson模型。

1.3.1 基于Nelson模型的直接估计法的验证

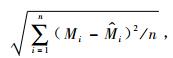
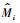
每一个建模数据中需要2个连续观测的可燃物含水率数据，每天连续观测15次，能够形成14个建模数据。为验证模型，每个可燃物样品分别取14, 28, 42, 56, 70, 84, 98和112个数据作建模数据，平衡含水率模型分别用Nelson模型，用Catchpole等(2001)方法估计出时滞和平衡含水率，分别对直径为D_0.5, D_1.0和D_1.5的10个样品的参数估计值的平均值、最大值和最小值对建模样本数作图，观察参数估计值随样本数的变化。对各个可燃物样品，用其估计的参数对其余多组含水率数据按天数分别验证，计算含水率预测的误差，计算多次验证的含水率误差的均值和变异系数，然后计算不同直径的10个样品含水率预测误差的均值和变异系数，用单个样品和直径平均的均值和变异系数对建模样本数作图，分析预测误差与样本数的关系和模型的稳健性。其中，误差采用均方根误差RMSE, RMSE=, M_i,为实测含水率，%; 为预测含水率，%；变异系数CV=σ/m, σ为含水率预测误差的标准差，m为误差的平均值，%。

1.3.2 基于Simard模型的直接估计法有效性分析

Simard模型为：

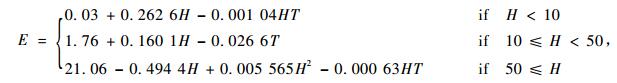
(6)

式中符号意义同前。

用Simard模型代替上述方法中的Nelson模型，与上同法，分析比较建模样本数不同时含水率预测效果的差异，并将基于2种平衡含水率模型的模拟效果进行对比。

上述统计利用SPSS 13.0统计软件和Excel软件完成。

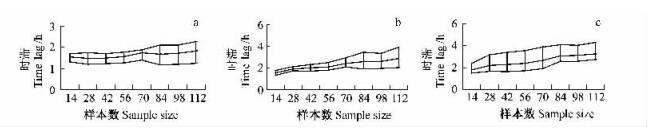
2 结果与分析 2.1 基于Nelson模型的方法验证

图 1表明，建模样本数为14的不同直径可燃物的平均时滞估计值为：1.5 h(D_0.5), 1.6 h(D_1.0)和2.0 h(D_1.5)。随建模样本数增大，同一直径可燃物时滞估计值略有增加，在样本数84以后，各直径等级可燃物的时滞为：1.3~1.7 h(D_0.5)、1.4~1.8 h(D_1.0)和1.5~2.4 h(D_1.5)。

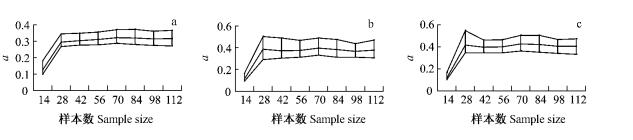
图 2表明，当建模样本数从14增加到28个以上时，参数a的估计逐渐稳定，波动范围为：0.27~0.34(D_0.5)、0.30~0.50(D_1.0)和0.34~0.55(D_1.5)，建模样本数为84时，波动范围为：0.28~0.37(D_0.5), 0.31~0.47(D_1.0)和0.35~0.50(D_1.5)。

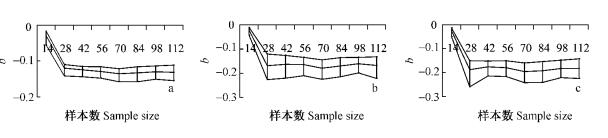
图 3表明，参数b随样本数的变化趋势与参数a大致相同，样本数28以后，估计稳定在：-0.15~-0.10(D_0.5), -0.22~-0.13(D_1.0)和-0.25~-0.1(D_1.5)。

由图 4可见，3种可燃物含水率预测误差的变化趋势相似，建模样本数为14时，误差为1.5%(D_0.5), 2.5%(D_1.0)和2%(D_1.5)；样本数28时，误差大幅下降，范围为：0.28%~0.57%(D_0.5), 0.44%~1.00%(D_1.0), 0.31%~0.77%(D_1.5)，均在0.1%以内。而后下降趋势趋缓，样本数84以后，误差稳定在：0.20%~0.36%(D_0.5), 0.27%~0.53%(D_1.0), 0.23%~0.39%(D_1.5)。

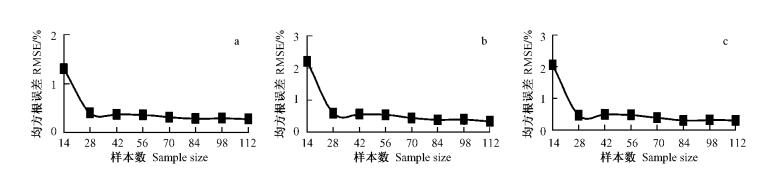
图 5表明，同直径10个可燃物样品的误差均值在建模样本数14时比较大，都超过2%，但样本数28时，减至0.4%(D_0.5), 0.58%(D_1.0)和0.46%(D_1.5)，而后有所减少，但趋势趋缓，当建模样本数增至84时，误差均值为：0.29%(D_0.5), 0.38%(D_1.0), 0.31%(D_1.5)。建模样本数再增加，误差变化不大。

图 6表明，单个可燃物样品含水率预测误差的变异系数变化趋势多数相同，个别有所不同(如样品5和6)。样本数28时，大部分变异系数有显著增加，波动范围为：0.4~0.56(D_0.5), 0.29~0.57(D_1.0), 0.31~0.65(D_1.5)，即误差分布在其均值的0.4~0.56倍(D_0.5), 0.29~0.57倍(D_1.0), 0.31~0.65倍(D_1.5)范围内。这之后，随样本数加大，3者误差变异系数开始缓慢回落，逐渐接近初始值，即误差分布更加集中，稳定度更高，见图 6。

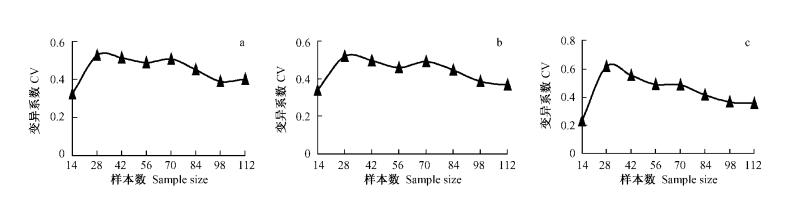
从图 7可见，3种直径的可燃物的误差变异系数均值在建模数据样本数28时最大，分别为：0.2(D_0.5), 0.17(D_1.0), 0.39(D_1.5)，而后随样本数增加而减少。结合图 4~6，当建模样本数小于84时，一些可燃物样品的含水率预测误差较大，或者不同样品之间的误差变化较大，当建模样本数为84时，各可燃物的含水率预测误差稳定在0.3%左右，且同样直径的不同样品之间的变化也很小，这说明建模样本数为84以上时，该方法的预测很稳定。在今后的应用中，建模数据至少要84个以上。

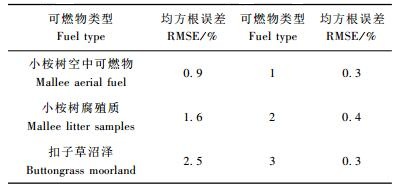
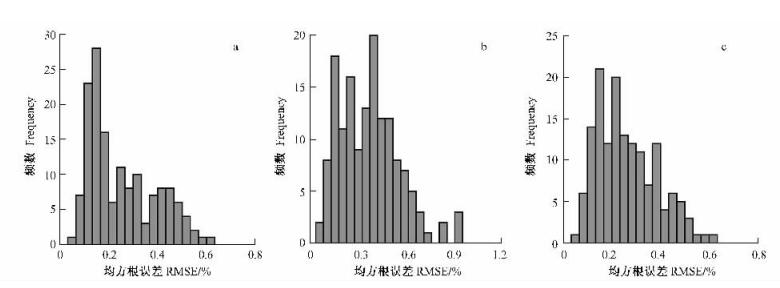
图 8给出建模样本数为84时不同直径可燃物的预测误差分布。此时，含水率预测误差小于Catchpole等(2001)的结果(表 1)，尤其对于直径0.5 cm和1.5 cm的枯枝。由误差分布图 8可知，可燃物含水率预测误差小于0.7%的频率为100%(D_0.5), 97%(D_1.0), 100%(D_1.5)。可见大部分误差在0.7%以内，只有直径1.0 cm可燃物有少部分高于0.7%，最大可达到0.91%。误差小于0.4%的频率为78%(D_0.5), 60%(D_1.0), 77%(D_1.5)。因此，误差在不同样品之间的分布是合理的，使用此方法的预测结果表明，多点均值具有地区代表性，建模样本数为14时偏差最大，该方法有较强的适用性。

2.2 基于Simard模型的直接估计法的有效性分析

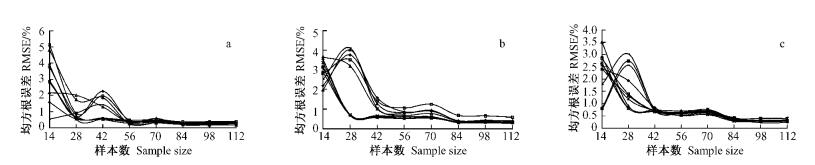
由图 9知，基于Simard模型的含水率预测误差和Nelson(1984)模型有相似的变化趋势，建模样本数为14时误差为3.0%(D_0.5), 3.0%(D_1.0)和2.5%(D_1.5)，然后随建模样本数增加而下降(样本数28时个别样本误差有小幅增大)，建模样本数84以后，误差也开始稳定，波动范围为：0.19%~0.37%(D_0.5), 0.30%~0.67%(D_1.0), 0.29%~0.42%(D_1.5)。

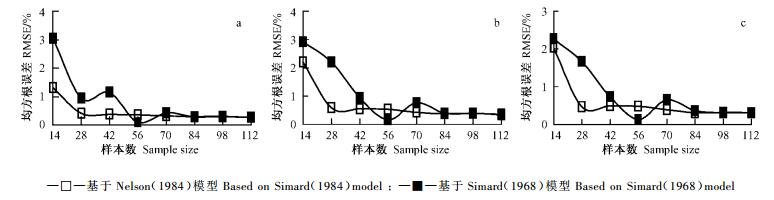
图 10表明，基于Simard模型的同直径可燃物样品误差均值在建模样本数为14时较大，为3.0% (D_0.5), 2.9%(D_1.0)和2.3%(D_1.5)，随样本数增加而下降，样本数84以后，误差均值稳定在0.28%(D_0.5), 0.39%(D_1.0)和0.36%(D_1.5)。可见，样本数量少时，基于Simard(1968)模型的误差均值高于Nelson模型，样本数超过84以后，2者差别不明显。

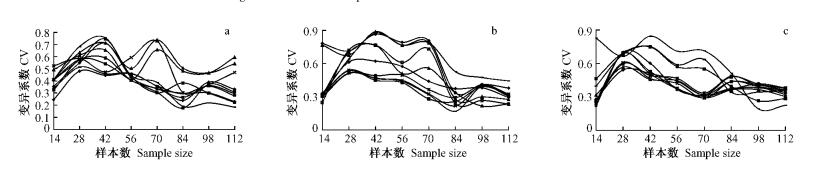
图 11表明，基于Simard模型的单个可燃物样品含水率预测误差的变异系数变化趋势多数相同，个别有所不同(如样品5和6)。建模样本数28时，大部分变异系数有显著增加，波动范围为：0.48~0.68 (D_0.5), 0.51~0.71 (D_1.0), 0.54~0.69 (D_1.5)，即误差分布在其均值的0.48~0.68倍(D_0.5), 0.51~0.71倍(D_1.0), 0.54~0.69倍(D_1.5)范围内。这之后，随样本数加大，误差分布更加集中，稳定度更好。

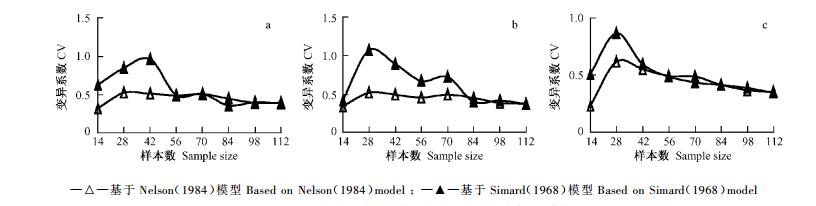
从图 12可见，基于Simard(1968)模型的3种直径的可燃物的误差变异系数均值在建模数据样本数28时最大，分别为：0.85(D_0.5), 1.1(D_1.0), 0.86(D_1.5)，而后随样本数增加而减少。当建模样本数小于84时，基于Simard(1968)模型的变异系数均值高于Nelson(1984)模型，超过84时，2者差别不明显。

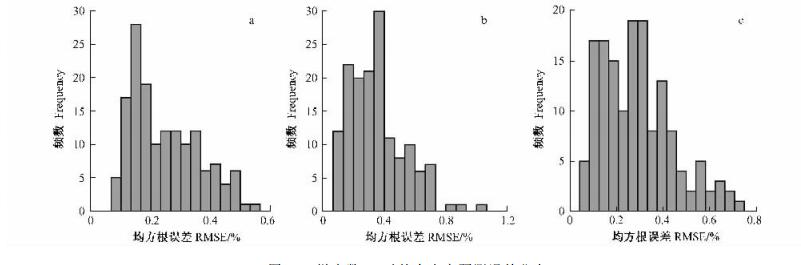
图 13给出建模样本数84时的不同直径可燃物的含水率预测误差分布。此时，基于Simard模型的含水率预测误差小于0.7%的频率为：100%(D_0.5), 96%(D_1.0), 100%(D_1.5)。可知大部分误差在0.7%以内，只有直径1.0 cm可燃物有少部分高于0.7%，最大可达到1.0%。变异系数为：0.36(D_0.5), 0.40(D_1.0)和0.41(D_1.5)，误差小于0.4%的频率为：89%(D_0.5), 67%(D_1.0), 66%(D_1.5)。综合上述分析，当建模样本数较少时，基于Simard模型的直接估计法不如基于Nelson模型的效果好，但当建模样本数超过84时，这2种的预测精度和适用性没有显著差异。

3 结论与讨论

本研究表明：1)基于Nelson模型的时滞和平衡含水率直接估计法在建模样本数较大时(至少84个)，时滞和平衡含水率响应函数的参数估计都比较稳健，且可燃物含水率的误差较小，说明该方法在利用观测数据直接预测含水率时具有很强的适用性，方法有效。但此时建模样本数要较大，建议80个以上。在误差标准要求不高时(如3%)，建模样本数取30左右也可适用。

2) 采用Simard模型直接估计可燃物时滞和平衡含水率时，在建模样本数较少时，其预测效果不如Nelson模型，但当建模样本数较多(超过84)时，2个模型预测效果没有显著差别。

需要讨论的是，本研究以方法验证为主要目的，本研究采用简单的、单一的可燃物小枝，所得结论有一定的理论价值。但野外可燃物结构十分复杂，特别是可燃物的微观结构、化学组成，包括表面蜡质、腐烂程度也影响可燃物的时滞和平衡含水率对环境因子的响应(Van Wagner，1969; Viney et al., 1989; Anderson, 1990)，这也是同一直径不同样本之间的参数估计差异和预测误差差异的一个原因。这些对直接估计法是否有一定的影响需要进一步研究。

2种平衡含水率模型对照结果表明，样本容量一定时，增加参数个数，将减小模型回归自由度，使参数估计稳定度降低，从而影响模型预测精度，参数个数、初始值和样本数等可能存在交互影响。这种交互作用需要进一步研究。