柴油车不但具有动力性和经济性好、性能可靠等优点，而且还可以减少约10%~20%的CH和CO排放，这大大吸引了人们对柴油车的关注；然而，柴油车微粒排放量约为汽油车的30~80倍，这种排放物严重地污染环境并危害人类健康(资新运，2000)。随着排放法规的日益严格，微粒捕集器(diesel particulate filter, DPF)技术是最终实现柴油机微粒排放控制的最为有效和简单的方法之一(Russo et al., 2008)。性能良好的DPF应该具备较高的过滤效率和较低的排气背压，并且在加热再生时具备很好的耐高温性能。DPF内的催化剂涂层可用来在低温时加强其被动再生能力，可减少加热再生所需能量，或者是可用来处理氮氧化物等的排气污染物。目前常用的过滤材料有堇青石蜂窝陶瓷、泡沫陶瓷、编织陶瓷纤维、金属丝网、金属纤维毡、碳化硅、氮化硅、活性碳纤维等，其中，最常用的过滤体材料为堇青石和碳化硅(Adler, 2005)。本文提出将碳化微米长木纤维作为过滤体材料净化柴油机尾气，理论和试验证明：该种材料所制成的尾气净化器过滤效率高，排气背压小，使用寿命长，可为柴油机尾气净化开辟一个新的方向。

1 碳化微米长木纤维

碳化微米长木纤维(carbonized micro-length wood fiber, CMLWF)是将高强度木纤维加工到微米厚度，将这样的微米长木纤维材料经一定的炭化工艺形成过滤芯，简称碳化微米长木纤维。

在木材的纳微米加工技术的研究中，当木纤维加工到微米厚度以后，纤维结构的重组将改变木材结构排列的形状，通过超薄加工的方法使木纤维结构发生有利于增加强度和韧性的方向调整过程，通过超精加工剔除木材本身天然缺陷(马岩，2001；马岩等，2003)。利用这种工艺加工的碳化木，不但具有高孔隙率、大的比表面积、较快的吸附脱附速度和较大的吸附容量, 而且碳化后表面具有不同的活性官能团, 在一定温度下对污染物有催化转化的作用，同时可去除氮氧化物和碳烟颗粒(Markus et al., 2009)。将经耐热处理的碳化微米长木纤维净化器与目前柴油车常用的堇青石微粒捕集器相比，具有价格便宜、耐腐蚀、微粒捕捉能力强、降噪效果好及耐热等特点。与活性碳微粒捕集器相比，最大的优点在于它具有较高的强度、整体工艺性好、成本低、更换方便、抗高温氧化能力及抗振性能好等特点。如果发挥碳化微米长木纤维吸附功能和降噪功能, 可望应用于柴油车，尤其是货车和客车的尾气净化, 这将是一个重要的、具有一定科学价值和经济效益的研究方向。

本文定义微米木长纤维的切削厚度在10~80 μm之间，切下的纤维长度在3~8 cm左右，宽度在3~10 mm的范围内。特别值得注意的是，越来越多的研究表明柴油车排放的小颗粒对人体健康危害非常大，因此，越来越多的国家关注机动车的小颗粒排放，而碳化微米长木纤维DPF可望成为未来解决小颗粒排放问题的有效方法之一。

2 碳化微米长木纤维DPF压降梯度理论计算方法

滤芯作为DPF的关键部件，气流在其中流动时涉及到气固两相流动、传热、传质以及燃烧等很多与流动特性有关的复杂过程和现象，而这也正是DPF设计和优化的关键依据和指标，所以研究气流在滤芯中的气流压降分布规律等流动特征对DPF的设计和优化非常必要。描述气流在DPF多孔滤芯上压降特性的研究较多，并建立了相应的公式(Pascal et al., 1997; Masoudi et al., 2000; Konstandopoulos, 2003)。一般来说，当滤芯的渗流速度较低时，压降分布规律与渗流速度满足线性关系，即达西定律；但是气流在滤芯中渗流速度较高时(孔径雷诺数R_ep>1~10)，惯性力相对于渗流阻力不能忽略，流体在多孔介质中流动时将偏离达西公式，呈现非线性特征(Pascal et al., 1997)。对多孔介质中非线性流动的描述，最常见的一种形式是Forchheimer-Ward(F-W)公式(Beavers et al., 1969)：

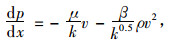
(1)

式中：dp/dx为压降梯度；μ为流体的黏度(Pa·s)；ρ为流过滤芯的气流密度(kg·m^-3)；k为渗透率；β为二次项系数。式中除流体的黏度μ和流过滤芯的气流密度ρ外，渗透率k和二次项系数β主要与多孔介质结构有关，一般由试验确定，也有一些经验的或半经验的以及理论预测的计算式(Bear, 1972; Kaviany, 1991)。

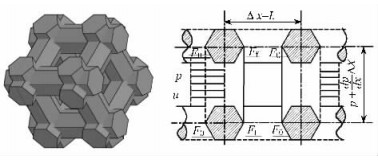
本文所使用的碳化微米长木纤维滤芯材料是一种经高温碳化处理的多孔木质滤芯，孔隙相互连通，纤维相互缠绕，形成微米木长纤维滤芯(马岩，2002), 纤维呈不规则的网络状纵横交错结构，要精确描述其几何结构很困难。为数学处理的方便, 根据结构特征, 将其从几何上简化成以一孔隙为中心的立体框架结构, 这一框架是由外接圆直径为d₀的正六棱柱连接而成, 形成规则的正立方单元体(简化的立体框架结构图及其二维示意图如图 1所示，计算时将正六棱柱近似成圆柱), 每一单元的边长为L, 由孔隙率定义和简化结构的几何关系可知：

(2)

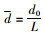
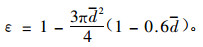
定义无量纲直径, 则

(3)

由于木材可以近似为横观各向同性，无序分布的滤芯介质内部纤维走向可以近似为各向同性，故可认为滤芯材料的平均孔径与方形通道的水力直径相等，即：

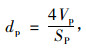
(4)

式中：S_P为等效单元流道中流体的总侧表面积。

将水力直径d_p定义成无量纲化，并根据d=d₀/L，方形通道的无量纲等效流通直径的数学模型建立在以下假设的基础之上:流过碳化微米长木纤维滤芯中的气流为不可压缩的、稳态流动的均质牛顿流体；过滤体骨架为各向同性的刚性材料，也即通道的结构和形状是各向同性且稳定的。可得：

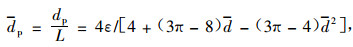
(5)

式中：d_p为方形通道的无量纲等效流通直径。

现设定气流宏观流向为x方向，如图 1所示。沿流向选取Δx=L的控制体，控制体在垂直于x方向的横截面面积为A=L²。所选取的控制单元上动量方程的矢量形式为(张鸣远等，2006)：

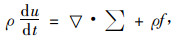
(6)

式中ρ为流过滤芯的气流密度(kg·m^-3)；∑为总表面力(N)；f为单位质量力(N·kg^-1)；u为气流流过滤芯中宏观流速(m·s^-1)。

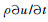
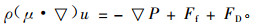
由流体连续性关系知，介质空间的流速u与流道内的流速v(渗流速度)之间应满足v=ε·u的关系。流体在滤芯中x方向做定常流动，故=0，流体在孔隙中流动时，受到的摩擦力F_f和形状阻力F_D等表面力以及流体自身的体积力F_B的作用。由于发动机尾气密度不大，可将其体积力F_B=ρf忽略，则式(6)化为：

(7)

式(7)左侧为密度与对流加速度项的乘积，由流体质点的运动以及速度在流场内分布不均匀引起，这里由于滤芯中流速并不高，相对于其他项很小，也可将其忽略；而单位体积流体受到的摩擦阻力为(华绍曾等，1985)：

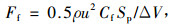
(8)

形状阻力(马岩，2002)：

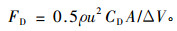
(9)

式中：ΔV为整个控制单元的体积；C_f为等效摩擦阻力系数；C_D为等效总形状阻力系数。

整个控制单元的体积ΔV=L³，由式(2)和式(4)可得流道总侧表面积为：

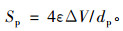
(10)

同时引入孔径雷诺数(张鸣远等，2006)：

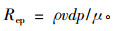
(11)

将式(8)~(11)代入式(7)，整理后得到：

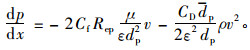
(12)

可以看出，式(12)与式(1)压降与渗流速度关系形式上是一致的。通过比较两式中的对应项，分别得滤芯材料的渗透率

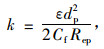
(13)

以及惯性项系数

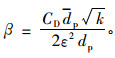
(14)

流体在流道中流动时，流速不高，雷诺数小于1 000，处于层流状态，可视为管内有黏性不可压缩的哈根-泊肃叶流动(张鸣远等，2006)，摩阻系数可表示为：

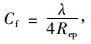
(15)

式中：λ为摩擦系数。

在R_ep≤2 000时, λ=64/R_ep。对于形阻系数C_D, 要根据简化的框架结构来解决, 因迎风形状阻力是由垂直于流动方向的六棱柱产生的, 这属于管内有阻碍物的流动阻力问题(华绍曾等，1985), 其阻力与阻碍物的截面形状、大小及其在管内的位置有关, 其形阻系数经简化表示为：

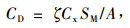
(16)

式中：C_x为阻流物体的阻力系数；ζ为考虑阻流物体在流道中的位置及孔型的修正系数；S_M为支杆的迎风横截面积。

C_x可在有关流阻手册中查到(Masoudi et al., 2000; Konstandopoulos, 2003)，根据实践经验，本文取ζ=0.7。在一单元体中, 进、出口阻流支杆总迎风面积为：

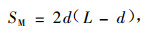
(17)

因此，式(16)便成：

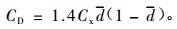
(18)

将式(13)和式(18)代入式(14)，可得到：

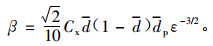
(19)

至此，对多孔介质的DPF滤芯来说，F-W公式中的待定系数，包括渗透率k和速度的二次项系数β皆已确定，即可通过求解式(12)而得到气流在滤芯上的压降特性。

3 渗流速度对DPF压降梯度的影响 3.1 试验设备与材料

试验是在车用柴油机6110A实验台架上进行的，所用的主要仪器包括气体流量仪(测定渗流速度)、微压计(测定压降梯度)和不透光烟度计(测定PM含量)等。试验中，分别对粗孔、中孔和细孔(分别标注为过滤体Ⅰ，Ⅱ，Ⅲ) 3种不同微孔径的CMLWF过滤体进行研究。6110A柴油机和3种CMLWF过滤体的主要参数见表 1。

3.2 压降梯度理论计算结果与试验结果比较

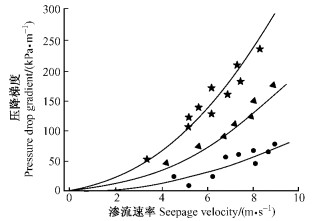
滤芯试件共有3个，分别选用Ⅰ，Ⅱ，Ⅲ 3种不同微孔径的CMLWF过滤体材料，都处于初始干净状态，截面积和长度分别都是2.01×10^-2 m²和100 mm。通过对3个滤芯上压降规律的理论计算和试验测量，分别得到滤芯上压降梯度与渗流速度的计算结果和试验结果，如图 2所示。

图 2表明，在孔隙率相近的情况下，滤芯的平均孔径越小，抛物线的焦距越大，意味着滤芯对气流的阻力随渗流速度增加而增加的速度越快。而DPF对PM的总滤除效率与孔隙直径成反比(资新运等，2000)，滤芯上的总压力损失和过滤效率都正比于其长度(王斌等，2003)，所以，在设计DPF滤芯时需慎重选择合适的孔径，做到过滤体捕集效率和压力损失之间的平衡，并且在外形结构允许的情况下，可以优先考虑孔隙直径较大、轴向长度较长的过滤介质，而不是孔隙直径较小、过滤体长度较短的介质，这样可以在满足同样过滤效果的同时，过滤体上的气流压力损失较小。

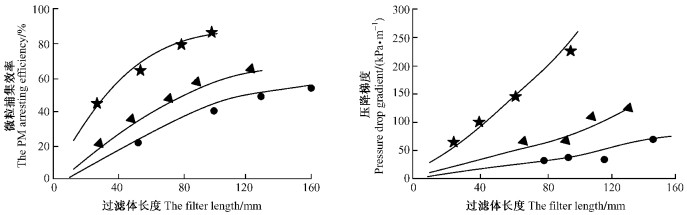
4 滤体长度对微粒捕集效率及压降梯度的影响

过滤体长度对微粒捕集效率及压降梯度影响的结果如图 3所示(柴油机转速2 000 r·min^-1, 负荷50%；过滤体横截面积2.01×10^-2m²)。增加过滤体长度，微粒捕集效率提高；但伴随着过滤体长度的增加，压降梯度也近乎直线上升。过滤体长度对细孔碳化木过滤体压降梯度的影响更加显著，当过滤体长度超过80 mm以上时，洁净的细孔碳化木过滤体的压降梯度已超过200 kPa·m^-1。粗孔碳化木过滤体的压降梯度较小，但微粒捕集效率也较低。

5 滤体横截面积对微粒捕集效率及压降梯度的影响

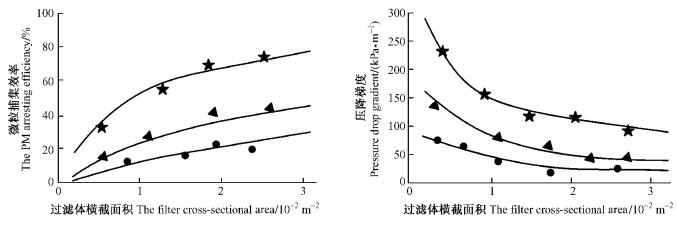
增加过滤体的横截面积，微粒捕集效率提高，同时压降梯度降低；细孔碳化木滤体的微粒捕集效率和压降梯度受过滤体横截面积的影响较大，试验结果如图 4所示(柴油机转速2 000 r·min^-1，负荷50%；过滤体长度50 mm)，增加过滤体横截面积主要受汽车安装空间的限制。

在碳化微米长木纤维过滤体中，惯性碰撞是柴油机排气微粒过滤捕集的主要机制，但从图 4中可以看到，随着过滤体横截面积的增加，微粒捕集效率逐渐升高，这显然是由于气体流速下降的缘故。当然，这一现象并非是过滤机制的改变，而是因为在高速气流作用下已沉积的微粒会发生重新分散，使微粒捕集效率下降。

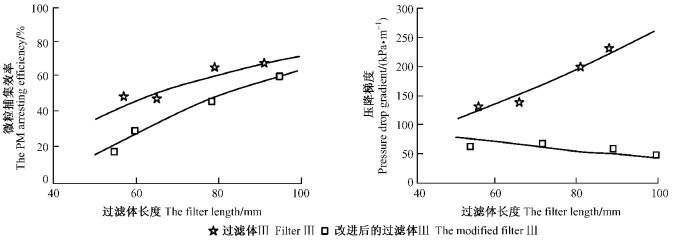
微粒在过滤体内的沉积规律与过滤体的细密度具有直接的关系。从过滤后过滤体不同剖面上看，粗孔碳化木过滤体各个横截面上所沉积的微粒基本一致；而在细孔碳化木过滤体中，微粒则主要集中在入口端附近。微粒大量沉积于入口端附近易造成堵塞，使压降梯度上升迅速。根据试验结果分析，采用细孔碳化木过滤体和增加其长度不失为提高微粒捕集效率的有效途径，但初始排气阻力的增加会缩短过滤体连续工作时间，对柴油机的性能也会产生不利的影响。另外，如果微粒主要集中在过滤体入口端附近，容易使过滤体在加热再生时因不均匀的热应力而损坏，而且整个过滤体长度也没有有效地加以利用。为解决细孔碳化木过滤体阻力大、微粒仅沉积在过滤体气流入口端附近的问题，本文采用特殊工艺，创造性地加工出从进口端到出口端孔径由大到小过渡的碳化木过滤体。将改进后的过滤体与细孔过滤体的微粒捕集效率和压降梯度进行对比，结果如图 5所示(柴油机转速2 000 r·min^-1，负荷50%，过滤体横截面积2.01×10^-2m²)。

从试验结果中可以看到，改进后过滤体的微粒捕集效率略有下降，但随着过滤体长度的增加，微粒捕集效率的损失逐渐减小；压降梯度则随着过滤体长度的增加而大幅度下降。其主要原因是改进后的碳化木过滤体的有效过滤面积增大、排气气流速度降低。过滤体越长，压降梯度降低的效果越明显。

6 结论

本文将碳化微米长木纤维作为滤体材料引入到DPF中，并建立CMLWF DPF多孔介质滤芯数学模型。通过理论和试验方法确定DPF压降梯度及捕集效率的影响因素，可为DPF设计提供设计依据。

1) 在设计DPF滤芯时需慎重选择合适的孔径，并且在外形结构允许的情况下，可以优先考虑孔隙直径较大、轴向长度较长的过滤介质。

2) 增加过滤体长度，微粒捕集效率提高；但压降梯度也近乎直线上升。过滤体长度对细孔CMLWF DPF过滤体排气背压的影响更加显著。

3) 增加过滤体的横截面积，微粒捕集效率提高，同时压降梯度下降；细孔CMLWF滤体的微粒捕集效率和压降梯度受过滤体横截面积的影响较大。

4) 为解决细孔碳化木过滤体阻力大、微粒仅沉积在过滤体气流入口端附近的问题，本文采用特殊工艺加工出从进口端到出口端孔径由大到小过渡的碳化木过滤体。试验结果表明，改进后的过滤体的微粒捕集效率略有下降，但随着过滤体长度的增加，微粒捕集效率的损失逐渐减小；压降梯度则随着过滤体长度的增加而大幅度下降。