1 Introduction

It is difficult to predict the prices, 50 or 100 years from now, of timber, pulpwood, and other products such as fuel from different species of trees. Furthermore, no one knows the extent to which different species will be able to survive and grow well after different future(but yet unknown)changes in the environment. How much worse will the state of the atmosphere become within a few decades? Will we experience even more acid rains? Will we see climatic changes? Will the pH value and temperature of the soil change very much during the next decades?

In the past few decades, there have been a large number of studies dealing with risk in forest management decisions. Adaptive optimization of the inter-temporal harvest and investment decisions is an active research area. Most of the studies have dealt with harvest and investment decisions when the timber growth and/or prices are stochastic.Descriptions and solutions of many different kinds of decision problems in the forest sector in a stochastic world, using adaptive optimization, can be found in the literature(Norstrom, 1975; Risvand, 1976; Lohmander, 1983; 1986; 1987; 1988; 1992; 1993; 2000; 2007; Brazee et al., 1988; 2000; Gong, 1994; Lu et al., 2003; 2005).

In a stochastic environment and for multi-stage decision problems, the options and flexibility have important values and meanings. The investment and harvest decisions in forestry are typical examples. Concerning the harvest decisions, forest resources naturally have flexibility because the mature age of a forest is not as strictly defined as that for most agricultural crops. It is for instance economically very important not to have to harvest during a year with exceptionally low prices. Two recent studies (Lohmander, 2007; Lohmander et al., 2008) showed how the flexible harvest year could be used to optimize the expected present value of forestry.

Flexibility may arise naturally or may come at an initial cost. Some kinds of flexibility can only be obtained via investments. Only when the value of flexibility is higher than the cost, the investment is cost effective. In forestry, one of the most important investment decisions is the selection of tree species. For a specific site, with the assumptions of certainty of timber prices and forest growth, there is often only one most suitable tree species which can maximize the utility of the forest owner, and therefore a single-species forest should be generated. In a stochastic environment, it is difficult to say which species is the best choice, since it depends on what will happen in the future. In such situations, the creation of mixed-species stands will increase the flexibility and provide options for future decisions. The option of adjusting the mixture of species is valuable, since the development of prices and environmental conditions cannot be predicted perfectly over a forest rotation period. Because of risks, we may benefit very much from delaying the final decisions about production until a point in time at which we will know more. The values of the flexibility and options depend on the properties of the stochastic processes of timber prices and forest growth. In a given situation, it is possible to analyze the costs and benefits of the investment to increase the flexibility(Lohmander, 1992; 1993; Carlsson, 1992).

Most types of fungi, insects, and other animals prefer some specific plant species, and, as a consequence, most kinds of damage to plants are species-specific. In Sweden, for example, the moose population usually prefers to eat pine plants. Clearly, it is valuable to have a mixture of species in the young forest in such cases(Lohmander, 1992; 1993).

Given such uncertainties, it is often optimal to increase the proportion of multi-species stands. Then, we have the option of selecting species during the final stage of production by selective thinning. The future decision about selection could be based on information that is not yet available, concerning the prices of products from different species, the future state of the environment and the future knowledge of environmentally dependent forest growth functions.

"True economics and true environmental concerns go hand in hand." The economic optimum in the face of future uncertainties is sometimes to invest in multiple species stands. This is also better for the environment in many ways because more species of animals and plants can live there(Lohmander, 1993).

Investing in a multiple species stand (instead of a single species stand) can create an option. One can then select which species to be kept growing in the stand at a later point in time. At that point, when the selective thinning takes place, there would have much more information concerning:

1) The development of the prices of different species because of new technology in the forest industry, new patterns of demand, etc.,

2) The growth of different species on different sites(considering earlier unknown changes in climate, acidity of soils, development of insects and fungi, etc.)

The aim of this study is to maximize the expected net present value through optimizing the planting density and the proportions of pine and spruce in the mixture, with and without the requirements of the Swedish Forest Act (Swedish Forest Agency, 2000) with the respect to stem number, and with stochastic damages from moose. The effects of stochastic price variations have been investigated, and differences in expected present value between multiple species stands and single species stands have been calculated. Through this study, the value of the option and flexibility of the mixed stands have been analyzed, and this will contribute to the better development of mixed stands, which naturally have advantage of ecological effects to the environment.

2 Method 2.1 Assumptions

To simplify the problem, the final harvest age has been set to 80 years, which is the lowest allowed harvest age (for some specified site indices and geographical regions) in the Forest Act. With typical parameter values, one can show that the lowest allowed harvest age is also the optimal harvest age, in the case that the legal constraint is considered. Without the legal age constraint, it would have been optimal to harvest earlier. Only one thinning is considered at age 40, and the thinning percentage is 40%(number of trees). When the price risk is incorporated, the price process is assumed to be a Martingale (Samuelson, 1965; Lohmander, 1987; 1992). The objective function in the next section is assumed to be concave.

2.2 The objective function

The objective function, , is the expected net present value per hectare. In the calculations, the unit Swedish Crowns, SEK, was used. However, any currency could be used in case the prices and costs are expressed in that currency.

where, n is the decision variable vector(the number of seedlings per hectare pine and spruce), N is the search scope, M₁ is the number of price scenarios, M₂ is the number of mortality levels, is the joint probability density function, s(j) is the moose damage mortality of different levels, C is the regeneration cost, R^t is the revenue from thinning, R^c is the revenue from clear cutting, l_v is the bare land value, p(i) is the price, t is the time of thinning, T is the time of clear cutting, and r is the discount rate.

2.3 Initial density search scope and optimization method

In this study, the decision variables were the initial density of pine and spruce. We set the initial density search scope for each of the two species to [0, 3000] per hectare. Thus, if the interval is 1, there are 3 001 density levels for each species and the combination of them gives 9 006 001 different levels. Accordingly, when one of the species has a density of 0, this will represent a pure stand. There are of course some levels which are not realistic among the possible combinations, such as both of the two species having very low levels or very high levels. This will not cause any problem becausesuch combinations would be eliminated through selection.

In order to simplify the optimization process, we developed a three-stage direct search approach as follows: a. The interval was set to 100 and the number of combinations to 961, and the rough optimized density combination was found; b. According to this result, the search scope was narrowed and the interval set to 10; it was searched again and a more precise result was found.c. The scope was narrowed again and the interval set to 1. The search was performed once more, and the final result obtained. This optimization process was based on the assumption that the objective function was concave.

2.4 Growth simulation

The growth process was divided into two stages. The first stage was from the establishment of the stand to age 40, while the second was from age 40 to the final harvest. The growth model of Pettersson (1992) was used for the first stage simulation. Given the site index, the only input needed for this model was the initial planting density, and the output was the total volume, mean diameter, and, most importantly, the stem distribution for each diameter class, which was necessary for the next stage of growth simulation. A mortality function was also included in the model to simulate normal mortality at this stage. However, this simulation approach was only approximate because the original models were used to simulate the pure pine stand and pure spruce stand separately. However, we used this model because the competition and the effects of two species on each other were less obvious in the first stage. In addition, this was the only model available to us.

For the second stage, the single-tree growth model of Söderberg(1986) was used to simulate the growth of trees in different diameter classes. The function of Bengtsson(1981) was used to estimate the natural mortality of the trees. When a thinning operation was included, the effects of thinning on the growth of the remaining trees were estimated by the function of Jonsson(1980)(The growth simulation models can be provided to interested readers on request).

Two products, saw timber and pulpwood, were considered for the two species. The following formula (Ollas, 1980) were used to estimate the yields of saw timber y_s and pulpwood y_p from 1 m³ of standing timber stock both for thinning and final felling:

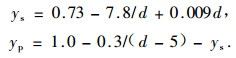
where, d denotes the basal area weighted mean diameter.

2.5 Mortality due to moose damage

According to the statistical data of Skogsstyrelsen(2002), the mortality ratedistribution caused by moose damage was calculated and shown in Tab. 1.

This mortality information was used in the simulation process.

2.6 Generation of price scenarios

The export prices of saw timber and pulp wood for pine and spruce from 1970 to 1994, which were adjusted by the producer price index (Statistics Sweden 2000) to the value of the year 2000, were used to calculate the expected price, the standard deviation, and the correlation between the products. The expected price was 575.20 kr·m^-3 for pine saw timber, 295.26 kr·m^-3 for pine pulp wood, 394.01 kr·m^-3 for spruce saw timber, and 294.79 kr·m^-3 for spruce pulp wood. The standard deviations were 92.41, 68.89, 43.20 and 35.82 for these products, respectively. The correlation coefficients between them were given in Tab. 2.

Two thousand price scenarios were generated using a Fortran random number generator, which wass ready to use function of the software, from the information given in Tab. 2. These price scenarios were used as realized prices when thinning decisions were to be made, and also used as the predicted prices at final cutting, as we assumed the stochastic price process to be a Martingale.

2.7 Other data

The study site was located in northern Sweden (latitude 65) and the site index was 22 (the dominant height equals 22 m at 100 years of age for pine). The fixed regeneration cost was 1600 SEK·hm^-2 and variable costs per seeding were 2.64 SEK. The variable harvest cost was 115 SEK·m^-3 for thinning and 75 SEK·m^-3 for clear cut, and the fixed cost for both of them was 2 000 SEK·hm^-2. The discount rate was 3%. The cost of transportation was 71 SEK·m^-3. The bare land value was 1 000 SEK·hm^-2.

2.8 Simulation process

A. The density and composition of pine and spruce were optimized assuming that there was no moose damage, no price risk and no thinning to be considered. This was compared with the corresponding pure pine stand with the same density. The gain of this comparison was purely due to the biological mixture effect.

B. While including moose damage in the optimization process, the optimized mixed stand was compared with a pure stand of pine. The gain in this case was then compared with that of step A.

C. According to the Forest Act, the stem number requirement at age 20, in this case 1 700, was added into the optimization. Steps A and B were then repeated. In the cases where the stem number was less than 1 700, a replanting of spruce should be done, and the fixed cost was half that of the planting while the variable cost was twice that of the planting.

D. Thinning decisions and price risk were then incorporated into the model. Two thousand price scenarios were used here. For each price scenario, there were four alternatives at the supposed time for the decision on thinning: a. thinning of pine; b.thinning of spruce; c.thinning of both species; and d. no thinning. The expected net present values for each of these four alternatives were calculated and compared, the one with the highest value being chosen for this price scenario. The average of these 2 000 price scenarios was then calculated. For pure stands only, two alternatives existed, thinning or no thinning.

E. Step D was repeated without price risk. The result was compared with that of D.

F. Step D was repeated with the transportation cost and harvest cost increased by 25%.

G. Step D was repeated with the transportation cost and harvest cost increased by 50%.

3 Results 3.1 Moose damage and the effect of mixing

Without moose damages, the mixed stand was still superior to the pure pine stand. When moose damage was included, this superiority was even more remarkable, as the mixed stand would have a higher resistance to the damage.

When moose damages are considered, the gain from a mixed stand over a pure pine stand will increase from 33% to 38% (Tab. 3).

3.2 Stem number requirement of the Forest Act

When the minimum stem number per hectare required by the Forest Act was added (in this case, 1 700), the superiority of the mixed stand was even greater(Tab. 4).

Regarding the problem of moose damages, there was certainly a much larger probability that a pure pine stand would be seriously damaged; If that happens, replanting, or even complete regeneration, was necessary. When mixed with spruce, this probability would be greatly reduced, because with the number of spruce stems, the least stem number requirement would be more easily satisfied.

3.3 The effect of selective thinning with price variation

When price risk and thinning operations were included in the analysis, the expected net present value increased due to the profits gained from price adaptive selective thinning.

The superiority of a mixed stand over a pure pine stand could be increased by 6% when price risk and selective thinning were included, compared to when the price was fixed. The NPV of a mixed stand increased by 4.2% with a variable price in relation to the case when we assumed that prices are fixed (Tab. 5).

3.4 Sensitivity to cost

The results of the analysis of sensitivity to cost were presented in Tab. 6 and Tab. 7.

If the transportation cost and harvest cost were increased by 25%, the result was different. The superiority of the mixed stand would increase by 8% when price risk was included. When the harvest cost and transportation cost increased by 50%, the result showed that with higher harvest cost, the superiority of a mixed stand over a pure pine stand was not substantially altered.

A comparison of the expected NPV of a mixed stand (between a variable price and a fixed price) showed that the gain from including the price risk was 14%. This was due to the Jensen Inequality Effect, and this effect was stronger in the cases where the expected price(net) was closer to zero than otherwise. This effect was reported also by Lohmander(1992; 1993).

The above results were based on the assumption that the plantation and seedling costs of pine and spruce were identical. This assumption may of course easily be modified if that is of particular interest in some area. In the investigated region, the cost of the labour involved in the plantation work was much larger than the cost of the seedlings, and the prices of the seedlings were the same. The value of the bare land was constant for both species because the same land was used in the test cases.

4 Discussion and conclusions

Optimal decisions are usually not the same under cases of risk and cases of certainty. This is true when we discuss forest plantation planning, thinning programs, final harvests, and many other forest management decision issues. As new information (concerning prices, costs, growth, physical damage, etc.) appears with time, which is typically the case in forest management decision issues, it is valuable to be able to adapt the management decisions to the latest information. Hence, it is important to create the best set of future options. These options deal with making optimal adaptive decisions based on the latest state of the forest stands, and of the world in general.

Product prices and production costs change rapidly. These cannot be predicted over the long periods of time and no "physical laws" can ever explain them. Future prices and costs are affected by inventions in processing technology and by general technological development. Inventions are, by definition, impossible to predict. Hence, it will never be possible to predict prices and costs perfectly. Thus, we have to regard future developments in prices and costs as stochastic processes. Optimal decisions in forestry and other fields should be based on the available information and degree of uncertainty concerning future developments.

The analysis in this paper represents one step in this direction. It has been found that the expected present value of the investment can be improved in typical forest management decision issues if we select a "flexible" multi-species plantation instead of a traditional "stiff" single-species plantation. The stochastic events to be taken into account, those necessitating adaptive decisions, were species-selective moose damages and market price variations. Clearly, other kinds of species-specific damages and other phenomena may occur during the life of the forest stand. The existence of these as yet unconsidered phenomena also implies that there may be more reasons for preferring multi-species forests to single species forests, which have not yet been completely described.