文章信息
- 梅志雄, 徐颂军, 王佳璆.
- Mei Zhixiong, Xu Songjun, Wang Jiaqiu
- 基于DRNN和ARIMA模型的森林火灾面积时空综合预测方法
- Spatio-Temporal Integrated Forecast Method of Forest Fire Area Based on DRNN and ARIMA Model
- 林业科学, 2009, 45(8): 101-107.
- Scientia Silvae Sinicae, 2009, 45(8): 101-107.
-
文章历史
- 收稿日期:2009-01-10
-
作者相关文章
2. 中山大学地理科学与规划学院 广州 510275
2. School of Geography and Planning, Sun Yat-Sen University Guangzhou 510275
森林火灾的预测预报对于森林防火和灭火指挥以及森林生态系统的保护具有重要的决策参考意义,国内外学者对其展开了广泛的研究,归纳起来主要包括2大类:一类是运用一些经验模型或基于统计回归法和时间序列预测模型等传统方法(Alexander,1987;Bianchinia et al., 2006;张智光,1999;张朝阳等,2006;曲智林等,2007)。这些方法主观经验占优、需要的数据量大且难以精确表达众多复杂的影响因素,特别是未考虑研究对象的空间拓扑关系,所以难以达到较理想的预测效果,并且这些方法非线性映射能力弱,对于不规则数据序列难以确定合适的模型结构;另一类是运用人工神经网络方法进行预测(温广玉等,2001;杨景标等,2005;黄家荣等,2007),人工神经网络具有自组织、自学习和泛化能力,无需考虑数学模型的内部结构、不需假设前提条件和人为地确定因子权重就可对林火等非线性动力学现象的任意非线性函数进行逼近和模拟,具有很广阔的应用前景。但目前的研究多以静态前馈BP网络或RBF网络对林火动态系统进行辨识,虽然有一定的效果,但其动态计算能力不强、不能直接反映系统动态过程的特性。
林火影响因素众多、相互作用复杂且随着时间和空间位置不同在动态变化,它是一个跨空间发展的动态过程,具有明显的时空特征,且具有复杂的随机性和非线性特征,不易被传统的分析方法和静态神经网络有效处理。因此对林火的预测需要运用时空预测方法。目前许多时空预测模型都是基于时间序列分析、空间统计分析等成熟的分析工具,然后分别进行时空扩展(Deutsch et al., 1986;Cressie et al., 1997;Pokrajac et al., 2001)。然而这些时空预测研究主要是针对具体问题的应用研究,未能有效解决时空预测的关键问题——同时无缝集成时间和空间预测,也不能处理森林火灾跨空间的动态变化过程。
为此,本文将使用具有更强的动态行为和计算能力、能处理跨空间动态变化的动态回归神经网络(dynamic recurrent neural network,DRNN)并结合自回归集成移动平均(autoregressive integrated moving average,ARIMA)模型来尝试对森林火灾成灾面积进行时空综合预测研究,旨在探讨有效的森林火灾预测技术,提高森林火灾管理水平。即首先用ARIMA模型对目标对象的时序进行预测,然后利用DRNN来捕获相邻对象间隐藏的空间相关性,最后用统计回归得到时空综合预测结果。
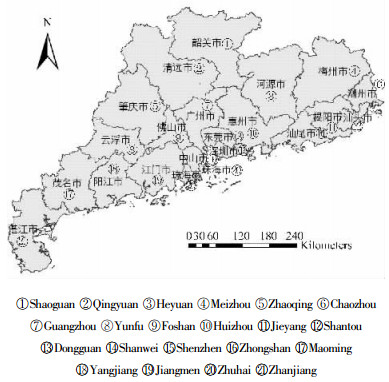
1 材料与方法 1.1 研究区及数据研究区域选取我国南方森林防火重点省份之一的广东省。广东地处温暖的南亚热带,秋冬2季气候干旱,空气干燥,属火灾易发区。1992年以来,全省森林防火工作面临着严峻形势。全省21个地市空间分布如图 1所示。
|
图 1 广东省21个地市空间分布图 Figure 1 Spatial distribution of twenty-one cities in Guangdong |
本文选择对森林防火预报起重要作用的森林火灾面积进行时空预测,研究所采用的实验数据是广东省各地市1992—2006年各年的森林火灾面积数据,资料来自《广东省农村统计年鉴》(广东农村统计年鉴编辑委员会,1993—2007)和广东省森林防火办公室。由于原始数据中有些地市的有些年份存在缺失值,所以用线性插值的方法对缺失的部分进行补缺,使数据完整。另外原始基础数据中各市间和不同年份间的数据相差比较大,若直接采用神经网络进行直接学习,势必造成学习结果不收敛,若直接用原始数据建模会造成很大的误差,所以计算前要对原始数据进行归一化处理。以归一化处理后的1992—2002年的森林火灾面积数据做训练样本,分别采用ARIMA模型和本文提出的时空综合预测方法对2003—2006年各市的森林火灾面积进行预测并进行比较验证。
1.2 空间预测方法——DRNN模型 1.2.1 DRNN的结构这是一种有反馈连接的动态神经网络,其输出不仅依赖当前到网络的输入,而且依赖于过去的输入和输出以及网络的当前状态,因而能反映动态映射,具有动态记忆能力,能够更直接生动地反映系统的动态特性,特别适合处理森林火灾等跨空间的动态行为,并且比静态前馈网络具有更强的计算能力(Mandic et al., 2001)。DRNN可用yt=f(yt-1,yt-2,…,yt-k,xt)表示,其中xt,yt分别表示t时刻的输入向量和输出向量,k表示时间延迟期数(McDonnell et al., 1994)。
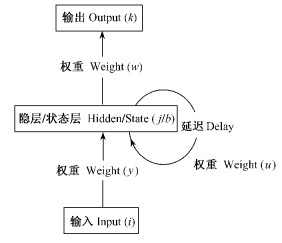
假如定义1个仅有1个隐层(状态层)和1个输出层而不包括输入层的2层节点的网络,输出层节点用k、隐层/状态层用j/b表示、输入节点用i表示,那么DRNN结构如图 2(Cheng et al., 2008)所示。从图 2可知,输入向量x经由一个权重层v传播,同时它又通过另一个回归权重层u与前一状态结合,网络的输出由状态和1组输出权重w决定。如果用Οj(t)表示t时刻第j个隐层节点输出,Ιj(t)表示t时刻第j个隐层节点输入,Οk(t)表示t时刻网络第k个输出层节点输出,Ιk(t)表示t时刻第k个输出层节点输入,那么DRNN输入输出映射关系可描述为(Cheng et al., 2008):
|
图 2 动态回归神经网络结构图 Figure 2 Structure of a dynamic recurrent neural network |

|
(1) |

|
(2) |
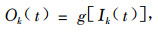
|
(3) |
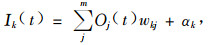
|
(4) |
式中:n为输入数量,m为状态节点数,α是偏置量,f,g分别为隐层神经元和输出神经元的传递函数。
1.2.2 DRNN空间预测原理在神经网络模型中,除去输入、输出变量外,最核心的变量就是各层之间的连接权重。连接权重通过模型对训练样本进行学习而获得,模型的内部参数本身并不具备实际意义。但如果把神经网络的输出比作要预测的空间单元i,神经网络的输入比作与预测的空间单元i有空间关联的空间单元j,i和j之间的连接代表空间相关性的度量,即空间权重w(i,j),那么用静态神经元来代表空间延迟算子就存在必然的合理性。
DRNN的输入与输出之间的连接代表了空间单元之间的联系,即空间相关性,输出空间单元i与邻域空间单元j之间的空间相关程度用空间权重w(i,j)度量,权值为0表示没有空间相关性,权值非0表示存在空间相关性。有多种定义空间权重的的方式(Anselin,1995),典型的规则有2种:1)基于邻接规则构建的邻接空间权重:包括基于rook(有共同的边界)方式、基于bishop(有共同顶点)方式、基于queen(有共同边界和顶点)方式;2)基于距离规则构建的空间权重:如果实体i和j的距离小于或等于指定距离,则认为i和j是相邻的。一般,邻接性由0和1两个值表达,w(i,j)=1代表i与j相邻,w(i,j)=0代表i与j不相邻。
可以用空间邻接矩阵W对线性“时空”神经网络的权值初始化,然后用反向传播算法和训练数据对初始权值进行训练,如果输入网络的空间邻接矩阵W能够正确地反映空间单元之间的关联程度,那么代表当前空间关系的初始化权值基本上不需要进行修正,否则,权值需要被归纳精化,以改进它在训练样本上的拟合度。这种方法能够有效地加快神经网络的收敛速度,容易使训练算法在假设空间中搜索到全局最优(Mitchell,2003)。当神经网络模型“学习”得到输入和输出变量的关系之后,即可用于对给定输入的预测。
1.3 时间预测方法——ARIMA模型ARIMA模型是Box-Jenkins提出的一种以随机理论为基础的精确度较高的时间序列预测方法(龚国勇,2008)。它把回归分析应用于时间序列,又不同于通常因果分析中的普通最小二乘法。ARIMA模型以数据序列平稳性为基础,对于有趋势的非平稳时间序列,经差分后消除其趋势,满足平稳条件,再使用ARIMA模型。
如果数据序列没有季节周期性规律,那么该模型可表示为ARIMA(p,d,q),其数学形式为:
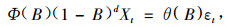
|
(5) |
式中:Φ(B)=1-φ1B-φ2B2-…-φpBp,θ(B)=1-θ1B-θ2B2-…-θqBq分别为平稳可逆ARIMA模型的自回归系数多项式、移动平滑系数多项式;B为后移算子;Xt为样本值;θq,φp为移动平均系数和自回归系数;εt为服从独立正态分布N(0,σ2)的白噪声序列;p,d,q分别是自回归阶数、差分次数、滑动平均阶数。
如果数据序列呈现季节周期性的变化特性,那么其模型为ARIMA(p,d,q)(P,D,Q),其数学方程为:
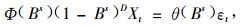
|
(6) |
式中:Φ(Bs)=1-φ1Bs-φ2B2s-…-φpBPs,θ(Bs)=1-θ1Bs-θ2B2s-…-θqBQs;P,D,Q分别是季节周期的自回归的阶、差分次数、滑动平均的阶,s是季节周期。
ARIMA建模与预测的一般步骤为:1)数据序列平稳化处理;2)模型的识别和定阶;3)参数估计和模型诊断检验;4)预测。
1.4 时空综合预测将单独的时间预测和空间预测整合到一起,可得到最后的时空综合预测结果。综合方法有很多种,对实际数据来说,方法简单,可能效率更高。一个好的综合方法要求单个模型本身的正确性、误差项的独立以及单个模型间存在较大的差异性。为了使结合保持易理解性并尽可能简单,可用线性回归(徐薇等,2005)来融合时间预测结果(YCt表示)和空间预测结果(YCs表示),产生最终的时空综合预测结果YCs-t:
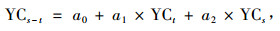
|
(7) |
式中:a0是回归常数,a1、a2是回归系数,它们可用最常用的最小二乘法来估计。如果原始数据使用最小二乘法进行系数估计导致参数取值范围非常大,就需要对模型中各个变量做标准化处理,使系数取值范围显著缩小。
2 结果与分析本文首先以广州市为例进行时空综合预测实验来说明建模过程,然后以相同的步骤和方法对其他地市进行时空综合预测。
2.1 采用ARIMA建立时间序列模型,获得时间预测结果对广州市1992—2002年的林火面积数据做时间序列分析,通过观察时间序列图,发现此序列非平稳但无周期性规律。经1阶差分处理后并经过ADF单位根检验发现数据序列趋于平稳,故差分阶数d取1。原序列{Xt}经一阶差分后的序列{Yt}已趋于平稳,对平稳序列{Yt}执行序列相关性检验,发现其自相关函数和偏自相关函数都是拖尾的,则可认为序列{Yt}产生于ARIMA过程,于是可建立ARIMA(p,d,q)模型,最佳p,q值需要运用AIC和BIC信息准则确定。经过反复试算,AIC=7.797,BIC=8.453时为最小,此时p=2,q=1,而差分阶数d=1已定。这样就得到广州市的森林火灾面积时间序列较理想的模型为ARIMA(2,1,1),然后利用非线性最小二乘法估计式(5)的模型参数,得到模型的具体数学方程为:

|
(8) |
式中:Yt是当前序列的值;Yt-1和Yt-2分别是1期和2期延迟序列的值;εt和εt-1是当前的残差和1期延迟的残差值。
模型中各参数估计的统计显著性采用t-检验均显著不为零;对残差执行序列相关性检验,发现残差的自相关函数和偏自相关函数都落在置信限为95%置信区间内,说明残差是随机分布的。进一步对模型的残差序列进行白噪声χ2检验,得到εt的χ2统计量为7.52、p值为0.037 2,εt-1的χ2统计量为26.35、p值为0.016 1,白噪声检验通过。因此,该模型通过临界值5%的残差自相关检验和白噪声χ2检验,表明模型拟合较好。用此模型得到广州市2003—2006年时间预测结果。
2.2 利用DRNN捕获相邻对象间隐藏的空间相关性,获得空间预测值进行空间预测要考虑研究区域的空间相关性,即设计DRNN的拓扑结构时要融入各市之间的空间关系。而由前面分析知,空间相关性可用空间邻接矩阵表示。空间邻接矩阵认为只有相邻的空间单元之间才有空间交互,它是2值(0,1)空间权重矩阵,如果2个空间单元相邻,则对应的连接元素赋值1,否则赋值0(刘旭华等,2002)。
那么,首先建立一个空间权重矩阵。由于研究区中各对象(各市)为面状空间单元,故测试了1阶基于rook方式、queen方式的邻接空间权重和使用不同阈值距离的基于距离的空间权重之后,发现基于rook方式(定义有共同边界的为相邻关系)的邻接矩阵关系能更好地拟合有公共边界的区域邻接。因此,依据图 1的多边形邻接性,采用1阶rook方式通过GeoDA软件建立了20×20空间邻接矩阵(图 3示),其中,0代表 1阶不邻接,1代表 1阶邻接。
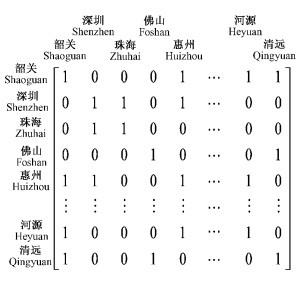
|
图 3 空间邻接矩阵 Figure 3 Spatial contiguity matrix |
接着,就要确定基于空间权重矩阵的DRNN的拓扑结构。考虑到研究区域的空间相关性,需构造3层神经网络。这里以广州市为例作为预测目标,那么广州市为该神经网络的输出层节点,其余20个城市为输入层节点,那么这20个城市的林火面积数据组成的序列为该神经网络的输入向量。这样,广州市的动态回归神经网络预测模型的结构为输入层节点数20个,隐层节点数20个,输出层节点数1个。Elman提出的Elman型DRNN在前馈网络的基础上,通过存储内部状态使其具备映射动态特征的功能,从而使系统具有适应时变特性的能力(Elman,1990;姜平等,2008)。它有表达短期记忆的激活反馈能力,状态层不仅随网络的外部输入而更新,而且随上一层向前传播活动而更新,反馈被一组权重修改以能通过学习算法进行调整,它是一种典型的动态神经元网络,既能学习时间模式又能学习空间模式(Elman,1990)。这里用它进行空间预测。
然后,采用1992—2002年的林火面积数据作为网络训练数据,根据训练和测试误差的分析,选取logsig函数为输出层转换函数,选取能反映空间关系特征的钟形的高斯radbas函数为隐层转换函数,选取trainlm函数为训练函数,选择网络学习效率为0.01。然后把数据输入Elman型动态回归神经网络进行训练,训练了127次达到训练目标,即达到了期望的学习误差(期望误差值是通过对不同期望误差网络的对比训练来选取的,这里经过多次对比训练,选取样本期望误差为0.08)。再把2003—2006年的利用ARIMA模型预测的数据作为Elman网络的输入进行测试,得到空间影响预测结果。
2.3 时空综合预测及精度评估进行了时间和空间预测后,再使用式(7)的线性回归模型来整合时间预测结果YCt和空间预测结果YCs,得到时空综合预测结果YCs-t(图 4)。图 4显示,该时空预测结果与实际观测数据基本一致,并且比单纯应用ARIMA模型预测精度高。

|
图 4 不同方法预测广州市结果比较 Figure 4 Comparisonof different forecast methods in Guangzhou |
可采用相对平方误差(RSE)、正态均方误差(NMSE)、均方根误差(RMSE)以及平均绝对误差(MAE)几个评价指标来衡量模型的预测效果,其计算公式为:
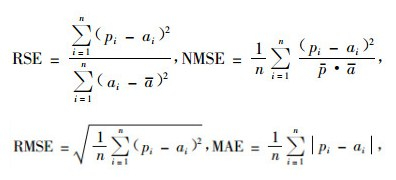
|
(9) |
式中:pi为预测值,ai为实际值,n为预测对象(城市)总数,p,a分别为预测值和实际值的平均值。
这样,用这几个指标对广州市森林火灾面积的ARIMA模型和本时空综合预测方法的预测结果进行评估,预测精度比较见表 1。时空综合预测方法的几个指标显然比ARIMA模型的小,预测效果更好。
|
|
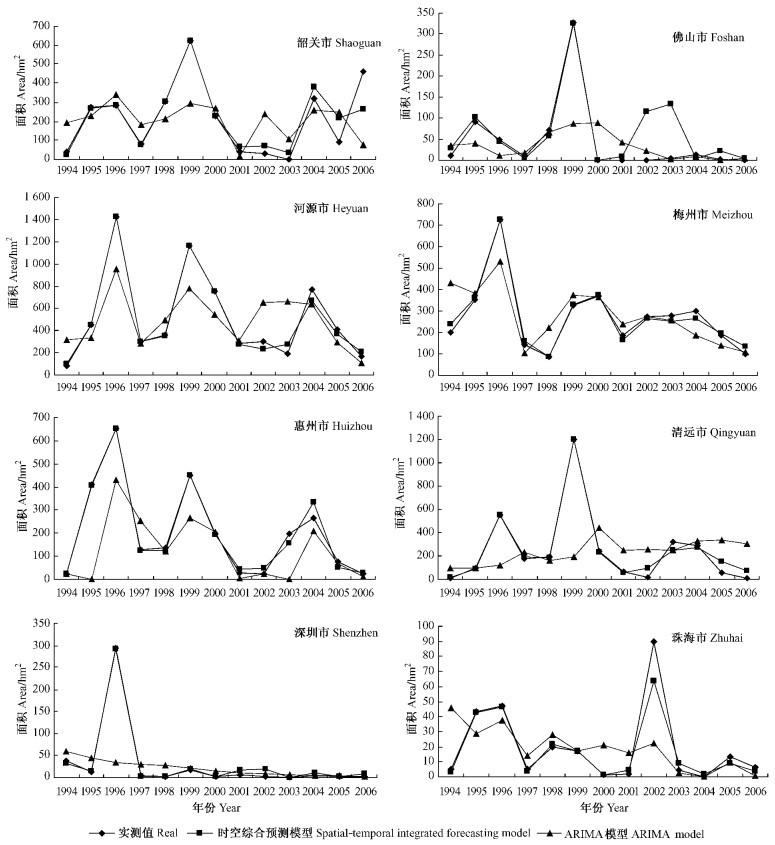
通过同样的步骤和方法可对其他每个城市森林火灾面积数据序列进行时空综合预测。但要注意的是,对不同的预测对象(城市),其ARIMA模型的形式和参数不同,并且其DRNN预测模型的结构及空间邻接矩阵也不同(在此不一一列出)。图 5列出了其他8个地市森林火灾面积的ARIMA模型、时空综合预测模型的预测结果与实际值比较情况,根据式(9)分别计算这8个城市的ARIMA模型和时空综合预测模型的预测结果的几个评价指标,得到表 2所示的预测精度比较结果。
|
图 5 不同模型预测8市森林火灾面积结果对比图 Figure 5 Comparison of forest fire area forecast in eight cities of Guangdong by different models |
|
|
图 5表明本时空综合预测模型和ARIMA模型都能拟合和预测每年森林火灾面积的变化,2个模型都能捕捉到森林火灾面积的变化趋势,但总体来看,本时空综合预测结果更加接近实际曲线一些,而ARIMA模型预测结果则相差较远。也有少数个别城市的个别年份的时空综合预测结果比ARIMA模型预测结果偏离实际值稍远,如佛山市的2002年和2003年的预测结果。其主要原因是该年份佛山市实际森林火灾面积数据缺失,但预测时通过插补使数据完整所造成的。表 2也显示出这8个城市的时空综合预测结果的RSE、NMSE、RMSE、MAE指标比ARIMA模型预测结果都有较大的下降。因此,该时空综合预测模型的预测精度明显优于ARIMA模型,这也说明模型考虑空间因素比只考虑时间因素更能提高预测的精度。此外,时空综合预测模型通过将空间邻接性或距离等先验知识嵌入到了DRNN设计当中,提高了模型收敛速度及可解释性。
总之,影响模型预测精度和可靠性的因素很多,主要有:1)样本自身因素。一般,训练样本数足够大、数据时间序列足够长,其预测值与实际值吻合度就越高。另外,样本时间序列波动大小、缺失情况也会影响到预测效果;2)空间相关性。一般考虑了空间影响比没有考虑空间因素预测精度更高,空间相关性越强,预测误差越小,预测精度越高;3)其他外界因素。林火受很多外界因素(如气象因子、地形因子、植被因子以及人为因子等)影响,且这些因子不断发生时空变化,而预测模型是依据历史资料建立的,随着预测时间的拉长,会影响到预测结果的可靠性。当然还有模型本身的缺陷,将在下文讨论。
3 结论与讨论本文将DRNN和ARIMA模型相结合,构建了一种森林火灾面积时空综合预测方法,并以广东省森林火灾成灾面积预测为例,说明其原理和具体建模过程,对预测精度进行了评估。结果表明:预测结果基本符合实际情况;由于考虑了数据间的空间关系,该时空综合预测方法可以对森林火灾面积进行较准确有效的预测,比单纯应用ARIMA模型有更高的稳定性和预测精度。
本研究也表明,该时空综合预测方法克服了单方面对时间或空间进行预测,或在此基础上进行时空扩展工作的限制,较好地解决了时空数据的问题,取得了较好预测效果。该方法非常适合森林火灾跨空间动态变化预测问题,是预测森林火灾面积的一种有效工具。并且该模型通过将空间邻接性或距离等先验知识嵌入到DRNN设计当中,提高了模型的收敛速度及可解释性。
由于数据获得困难,本文仅对林火面积单一变量进行预测,而林火发生的因素众多且不断变化,随着预测时间的拉长,该方法的稳定性必会受到影响,因此,需要考虑多因素影响且及时补充新的资料来修正预测模型;本文使用的神经网络结构、网络参数对预测的稳定性也有一定影响,需要改进网络结构、优化网络参数等来优化预测模型,从而提高预测的准确度和稳定性;空间权重矩阵定义的标准不同也对预测和分析结果的稳健性有一定的影响;此外,本文只采用线性回归方法整合时间预测和空间预测结果,为了进一步提高预测精度和稳定性,需要探索其他的融合方法。这些有待于进一步研究。
龚国勇. 2008. ARIMA模型在深圳GDP预测中的应用. 数学的实践与认识, 38(4): 53-57. |
黄家荣, 刘倩, 高光芹, 等. 2007. 森林火灾成灾面积的人工神经网络BP模型预测. 河南农业大学学报, 41(3): 273-275. DOI:10.3969/j.issn.1000-2340.2007.03.007 |
广东农村统计年鉴编辑委员会.广东农村统计年鉴.1993—2007.北京: 中国统计出版社.
|
姜平, 石琴, 陈无畏, 等. 2008. 基于Elman型回归神经网络的公交客流预测. 合肥工业大学学报:自然科学版, 31(3): 340-342. |
刘旭华, 王劲峰. 2002. 空间权重矩阵的生成方法分析与实验. 地球信息科学, (2): 38-44. DOI:10.3969/j.issn.1560-8999.2002.02.008 |
曲智林, 胡海清. 2007. 基于气象因子的森林火灾面积预测模型. 应用生态学报, 18(12): 2705-2709. |
温广玉, 侯锡铭, 陈华豪. 2001. 人工神经网络在林火发生预报中的应用. 生物数学学报, 16(2): 225-228. DOI:10.3969/j.issn.1001-9626.2001.02.017 |
徐薇, 黄厚宽, 王英杰. 2005. 一种基于数据融合和方法融合的时空综合预测算法. 计算机研究与发展, 42(7): 1255-1260. |
杨景标, 马晓茜. 2005. 基于人工神经网络预测广东省森林火灾的发生. 林业科学, 41(4): 127-132. DOI:10.3321/j.issn:1001-7488.2005.04.022 |
张朝阳, 林启训. 2006. 集成预测模型在森林火灾预测预报中的应用研究. 中国农学通报, 22(2): 400-403. |
张智光, 陶冶, 叶超飞. 1999. 森林火灾受害面积的灰色预测模型的研究. 林业科学, 35(5): 124-128. DOI:10.3321/j.issn:1001-7488.1999.05.022 |
Alexander M E. 1987. Canadian forest fire behaviour prediction system. Forest Service, (3): 92-96. |
Anselin L. 1995. Local indicators of spatial association-LISA. Geographical Analysis, 27(2): 93-115. |
Bianchinia G, Denhama M, Cortésa A, et al. 2006. Improving forest-fire prediction by applying a statistical approach. Forest Ecology and Management, 234(S1): 210. |
Cheng T, Wang J Q. 2008. Integrated spatio-temporal data mining for forest fire prediction. Transactions in GIS, 12(5): 591-611. DOI:10.1111/tgis.2008.12.issue-5 |
Cressie N, Majure J J. 1997. Spatio-temporal statistical modeling of livestock waste in streams. Journal of Agricultural, Biological and Environmental Statistics, 2(5): 20-28. |
Deutsch S J, Ramos J A. 1986. Space-time modeling of vector hydrologic sequences. Water Resources Bulletin, 22: 967-980. DOI:10.1111/jawr.1986.22.issue-6 |
Elman J L. 1990. Finding structure in time. Cognitive Science, 14: 179-211. DOI:10.1207/s15516709cog1402_1 |
Mandic D P, Chambers J A. 2001. Recurrent neural networks for prediction: learning algorithms, architectures, and stability. Chichester: John Wiley & Sons.
|
McDonnell J R, Waagen D. 1994. Evolving recurrent perceptrons for time-series modeling. IEEE Transactions on Neural Networks, 5: 24-38. DOI:10.1109/72.265958 |
Mitchell T M. 2003. Machine Learning. New York: McGraw-Hill.
|
Pokrajac D, Obradovic Z. 2001. Improved spatial-temporal forecasting through m o deling of spatial residuals in recent history//Robert G. Proceedings of the First International SIAM Conference on Data Mining, Chicago, Illinois: 368- 386.
|
 2009, Vol. 45
2009, Vol. 45


