近年来, 空间格局已经成为生态学研究的热点之一(Turner, 1989; Dale, 1999; Liebhold et al., 2002), 其变化可以揭示潜在的生态学过程(Levin, 1992; Perry et al., 2002). 在植物生态学中, 植物的空间格局分布可能是由不同的生态学过程诸如种子扩散、种内(间)竞争、干扰或环境异质性等引起(Sterner et al., 1986; Kenkel, 1988; Jeltsch et al., 1999; Klaas et al., 2000), 由于大部分植物个体固定生长在某一位置, 不会从一个生境移动到另一个生境, 因此邻近植物间关系可以从不同角度上反映潜在的生态学过程. 目前植物空间关系分析最常用的方法是植物空间点格局分析(Ripley, 1981; Stoyan et al., 1994; Diggle, 2003), 其计算方法和模型已经得到了广泛应用(Kenkel, 1988; Jeltsch et al., 1999; Klaas et al., 2000), 国内也已经应用这一方法开展了相关研究(张金屯, 1998; 杨洪晓等, 2008; Yu et al., 2009). 然而该方法的不足之处是研究的所有植株无论大小均被概化为一个点, 当植株与研究区域相比较小时, 这种概化所产生的误差是可以忽略的, 而当植株的大小足以影响到所研究的生态学过程(例如植物间小尺度的空间关系)时, 这种概化可能会导致错误的结论(Simberloff, 1979; Prentice et al., 1985; Purves et al., 2002). 鉴于此, Wiegand等(2004)在空间点格局分析方法的基础上提出了基于栅格的方法来分析不规则形状物体的空间格局. 本研究以鄂尔多斯高原北缘2个典型植被地理区域的白刺(Nitraria tangutorum)沙堆为研究对象, 在对该方法详细描述的基础上, 分析了2个区域白刺沙堆的空间分布格局特征, 比较了常规点格局分析方法和基于栅格的点格局分析方法的差异, 探讨基于栅格的空间点格局方法在干旱半干旱地区灌木(丛)研究中应用的可行性.

1 研究区概况

研究区位于内蒙古自治区鄂尔多斯市杭锦旗境内鄂尔多斯高原北缘库布齐沙漠与黄河间的沙漠-河岸过渡带上(107°10′—108°45′E, 40°23′—40°41′N). 研究区东部年降水量400 mm以上, 而西部边缘则在150 mm以下; 年蒸发量2 000~2 700 mm, 为降水量的6~17倍; 年平均气温5~7 ℃, 东低西高, 年平均风速3.5 m·s^-1, 春季增大到4.1 m·s^-1. 全年风沙日45~75天, 春季占一半以上(李博, 1990; 牛建明等, 1998). 区域东部地带性土壤为栗钙土, 西部地带性土壤则为棕钙土, 河漫滩上分布着不同程度的盐化浅色草甸土. 东部地带性植被为草原, 西部为荒漠, 河漫滩盐化草甸土上生长了大面积的盐生草甸(李博, 1990), 在这个典型的生态过渡带上(东西长约200 km, 南北宽几十米到几千米不等)分布着白刺群落.

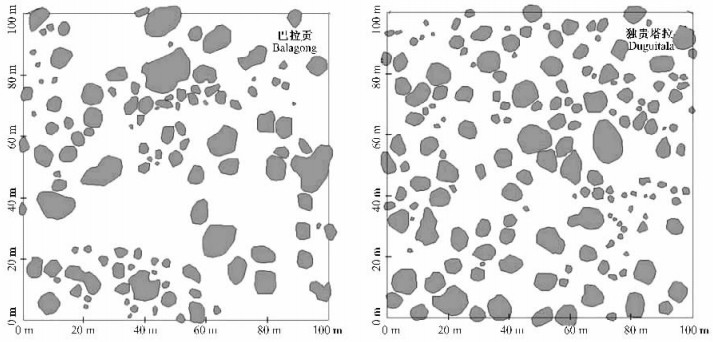
2 研究方法 2.1 样地设置

在研究区内的巴拉贡镇(107.17°E, 40.39°N)和独贵塔拉镇(108.75°E, 40.54°N)附近分别选择1个100 m×100 m样地, 2个样地分别代表干旱区和半干旱区的白刺群落, 样地内除了白刺沙堆所形成的微地形起伏外, 其余地段均比较平坦. 将每个样方划分为10 000个1 m×1 m的小样方, 根据每个小样方内白刺沙堆的分布状况, 在方格纸上绘制样地内沙堆外围廓线(图 1).

2.2 统计分析

采用Wiegand等(2004)提出的基于栅格的空间点格局方法进行分析, 选用的函数为Ripley K及L函数和点对相关g函数, 2类函数的区别在于前者为以圆为计算范围的累计函数, 后者为以圆环为计算范围的非累计函数(Stoyan et al., 1994; Wiegand et al., 2004), 以往的研究表明2个函数间可以相互补充, 从而使得分析结果更为准确客观(Condit et al., 2000; Schurr et al., 2004). Wiegand等(2004)给出的双变量K函数的计算公式如下:

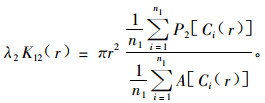
(1)

式中: λ₂为研究区内变量2的点的强度; r为圆的半径; n₁为研究区内变量1的总点数; i为研究区内变量1的第i个点; C_i(r)为以第i个点为圆心, r为半径的圆; P₂[C_i(r)]为圆C_i(r)内变量2的总点数; A[C_i(r)]为圆C_i(r)的面积; 后两者的计算公式如下:

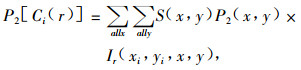
(2)

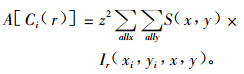
(3)

式中: S(x, y)为判别因子: 当坐标为(x, y)的栅格位于研究区内时, S(x, y)=1, 否则, S(x, y)=0; P₂(x, y)为圆C_i(r)内栅格数据中变量2的点数; (x_i, y_i)为变量1的第i个点的坐标; z²为单位栅格面积; I_r(x_i, y_i, x, y)为计数变量, 用来定义以第i个点为圆心, r为半径的圆, 其计算公式如下:

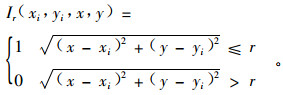
(4)

根据公式(1), L函数可以通过下式估算:

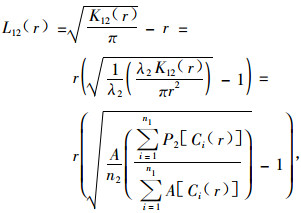
(5)

式中: A为研究区面积, n₂为研究区内变量2的总数.

双变量的点对相关g函数及其衍生出的O函数可以通过下式估算:

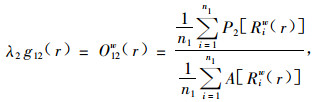
(6)

式中: w为圆环宽度; R_i^w(r)为以变量1中第i个点为圆心, r为外环半径, 宽度为w的圆环; P₂[R_i^w(r)]为圆环R_i^w(r)内变量2的总数; A[R_i^w(r)]为圆环R_i^w(r)的面积. 其中后2项的计算可采用公式(2)和(3), 但公式中的计数变量I_r(x_i, y_i, x, y)用I_r^w(x_i, y_i, x, y)代替, 其计算公式如下:

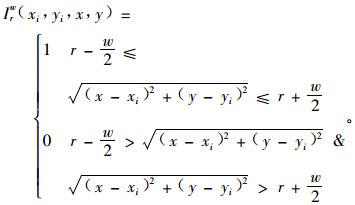
(7)

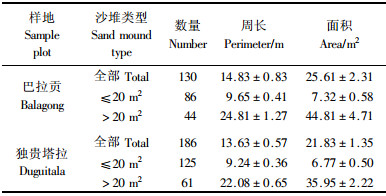
本研究中, 将白刺沙堆按面积分为2类, ≤20和>20 m²(表 1). 首先采用单变量分析方法对所有的白刺沙堆和2类白刺沙堆分别进行格局分析, 计算仍采用上述公式, 所不同的是将公式中的变量2用变量1来代替, 且在L函数的计算时, 作为圆心的点并不计入, 研究中采用完全空间随机模型(CSR)对结果进行显著性检验. 对均质的Poisson过程而言, L(r)>0表示在距离r的范围内为聚集分布, L(r) < 0表示在距离r的范围内为均匀分布, g(r)>1表示在距离r处为聚集分布, g(r) < 1表示在距离r处为均匀分布. 为了揭示2类白刺沙堆间相互作用的关系, 采用双变量分析方法进行分析, 选用“前期状况(antecedent condition) ”零模型对结果进行显著性检验, 该零模型在>20 m²白刺沙堆位置固定不变的前提下, 对≤20 m²白刺沙堆的位置进行随机分布, 但其位置并不与>20 m²白刺沙堆的位置重叠, 该零模型多用来测试不同大小的同种植物间的相互关系(Wiegand et al., 2004), 计算结果中L(r)>0表示在距离r的范围内为相互促进, L(r) < 0表示在距离r的范围内为相互竞争, g(r)>1表示在距离r处为相互促进, g(r) < 1表示在距离r处为相互竞争.

同时对概化为点的白刺沙堆的空间格局进行分析, 并将其结果与上述分析结果进行比较, 所有分析过程均采用Programata程序进行(Wiegand et al., 2004; Wiegand et al., 2006), 上述的零模型均采用99次随机过程来计算其置信区间.

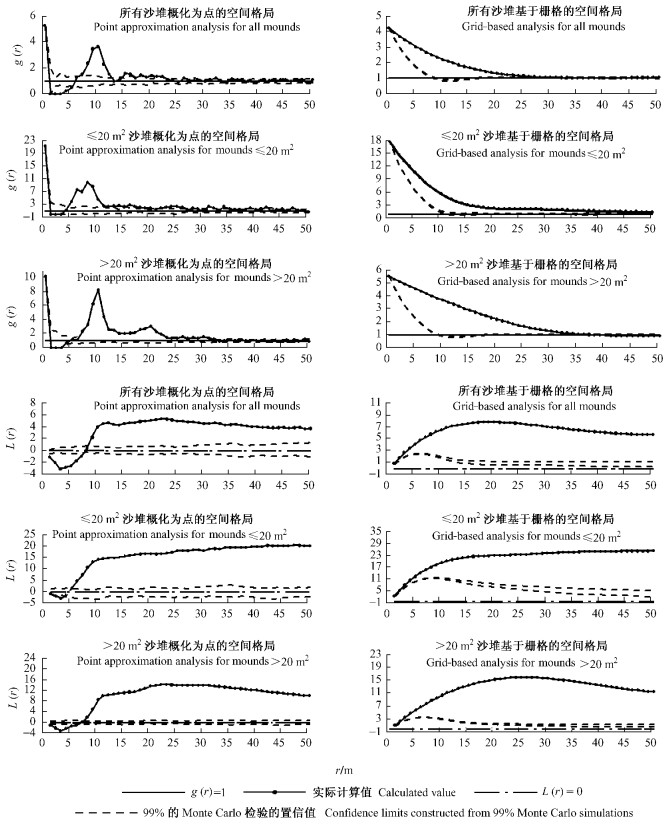
3 结果与分析 3.1 单变量分析

巴拉贡: 基于栅格的空间格局的分析结果表明, 就g函数而言, 所有沙堆在距离1~34和44~50 m处呈显著聚集分布, 面积≤20 m²沙堆在所有距离处均呈显著聚集分布, 而面积＞20 m²白刺沙堆则在距离1~36 m处呈显著聚集分布, 在40~50 m处呈显著均匀分布, 且随着距离的增加, 函数值呈逐渐下降的趋势(图 2); 就L函数而言, 3者在所有距离内均呈显著聚集分布, 随着距离的增加, 全部沙堆和>20 m²沙堆呈现先增加后降低的趋势, 并分别在20和25 m处达到最高值, 而≤20 m²沙堆则一直呈现增加的趋势. 从概化点格局的分析结果来看, 3者的g函数分别在较近距离处(1~5, 1~3和1~4 m)呈显著均匀规则分布, 在较远距离处(6~22, 5~36和5~32 m)呈聚集分布(>20 m²沙堆为不显著聚集分布, 所有沙堆和≤20 m²沙堆为显著聚集分布), 在其他距离处则基本上为随机分布; 3者的L函数分别在较近距离内(1~7, 1~4和1~6 m)呈均匀分布, 而在较远距离内(9~50, 5~50和8~50 m)呈显著聚集分布.

独贵塔拉: 与巴拉贡的分析结果相似, 从基于栅格的空间格局的分析结果来看, 全部、≤20 m²和>20 m²沙堆的g函数分别在距离0~18, 0~40和0~28 m处表现为显著聚集分布, 此后基本上为随机分布, 且随着距离的增加, 函数值呈逐渐下降的趋势; 3者的L函数值在所有距离尺度内均表现为显著聚集分布, 且总体变化呈现先增加后降低的趋势, 并分别于12, 16和20 m处达到最高值. 概化点格局的分析结果表明, 在较近距离处(1~5, 1~4和1~5 m)所有沙堆和>20 m²沙堆的g函数呈显著均匀分布, 在中等距离处(7~11, 5~19和7~21 m)所有沙堆和>20 m²沙堆的g函数呈显著聚集分布, 在其他尺度上3者的g函数基本上为随机分布; 较近距离内(1~7, 1~4和1~5 m)所有沙堆和>20 m²沙堆的L函数呈显著均匀分布, 此后的距离内3者的L函数基本上均呈显著聚集分布(仅全部沙堆在31~37 m内不显著).

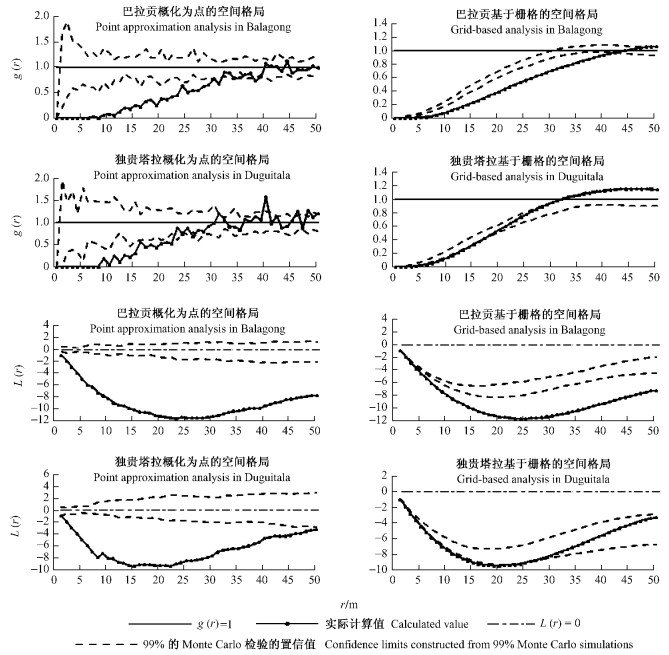
3.2 双变量分析

巴拉贡: 基于栅格的空间格局分析结果表明: 面积大小不同的白刺沙堆间g函数在较近距离处(0~4 m)呈不显著竞争关系, 在中远距离处(5~42 m)则呈显著竞争关系, 仅在更远的距离处(43~50 m)呈不显著促进关系; L函数则在所有距离内呈显著竞争关系. 概化点格局的分析结果表明: g函数在中近距离处(0~31 m)呈显著竞争关系, 在中远距离处(32~39 m)呈不显著竞争关系, 在较远距离处(40~50 m)则基本上呈随机状态; L函数仍在所有距离内呈显著竞争关系(图 4).

独贵塔拉: 基于栅格的空间格局分析结果表明: 面积大小不同的白刺沙堆间g函数在中近距离处(2~31 m)表现为不显著竞争关系, 而在中远距离处(32~50 m)呈促进关系, 但这种关系仅在32~34 m范围内较为显著; L函数在所有距离内呈竞争关系, 但仅在中近距离内(1~24 m)较为显著. 概化点格局的分析结果表明: g函数则在中近距离处(0~22 m)呈显著竞争关系, 而在中远距离处(23~50 m)基本表现为随机分布; L函数在所有距离内呈显著竞争关系(图 4).

4 结论与讨论

基于栅格的空间点格局单变量分析结果中2个函数在较近距离所反映的聚集程度均较概化点格局的分析结果明显(图 2, 3), 而双变量分析结果中2种函数则在较远距离表现出一定的差异, 因此基于栅格的空间点格局方法在研究近距离的植物群落的同种个体单变量空间格局时更为适用(Purves et al., 2002).

单变量格局分析结果表明, 2个样地中无论是全部还是面积大小不同的沙堆均以聚集分布为主, 这与以往干旱半干旱区灌木分布格局的研究结果相似(Prentice et al., 1985; Couteron et al., 1997), 由于2个样地的地形比较平坦, 可以推断这种聚集分布的结果不是由于样方中资源分布异质性引起的, 而是由潜在的生态学过程如群落演替过程中种子的扩散过程形成的(Ludwig et al., 1988). 在研究区内种子的扩散过程主要是由风力驱动的, 前期形成的白刺沙堆一方面可以改变风沙流的特征, 促使从上风向其他沙堆吹来的白刺种子在沙堆周围降落并有可能萌发, 另一方面在沙堆的背风处会形成一个比较适宜的小环境, 为本沙堆的落种提供了一个较为适宜的萌发环境, 这就是沙漠生态系统中所谓的庇护植物的效应(Jordan et al., 1979; Valiente-Banuet et al., 1991), 这种庇护效应不仅发生在不同的植物种间, 在同种植物的成年植株和幼苗间也同样存在.

本研究对2个样地中不同面积大小的白刺沙堆进行了双变量格局分析. 就基于栅格的空间格局分析方法而言: 2个样地的g函数在较近和中等距离处表现为竞争关系, 在中等和较远距离处呈现为促进关系, 所不同的是, 巴拉贡的中等距离的竞争关系较为显著; 而L函数由于其累积效应的影响, 在中远距离处的促进关系为中近距离处的竞争关系所掩盖, 因此在所有距离内均表现为竞争关系, 这种竞争关系在巴拉贡所有距离内均为显著, 在独贵塔拉仅在中近距离内(1~24 m)较为显著, 造成上述结果的主要原因是随着群落中新萌出的白刺幼苗生长并逐渐形成新的白刺沙堆, 其对资源特别是水分的需求逐渐增加(由于巴拉贡位于干旱区, 其降水量显著低于半干旱区的独贵塔拉, 因此其竞争关系显著高于独贵塔拉). 就概化点格局的分析方法而言: 与前者不同的是g函数在中远距离处表现出不同程度的随机分布, 而不是促进关系, 造成这种差异的主要原因是方法本身造成的还是白刺群落所处的演替阶段所导致的, 有待于进一步探讨.

近年来, 遥感技术的飞速发展使得一些高分辨率的影像数据获取成为可能, 通过遥感影像提取植物个体的详尽信息为许多生态学研究提供了较为翔实可靠的数据(Nagendra, 2001; Holmgren et al., 2003; Carleer et al., 2004; Foody et al., 2005). 在植物比较稀疏的干旱半干旱地区, 由于客观条件的限制, 有时很难对植物的大小进行实地量测, 退一步说即使可以开展植被调查工作, 也只能进行小面积的调查, 而大面积的调查工作需要依靠目前比较成熟的遥感技术, 通过图像处理技术并结合适当的数学模型, 对不规则形状植物个体的空间信息进行提取, 进而对其空间格局进行分析(Strand et al., 2006; 2007; Atkinson et al., 2007), 本文所采用的基于栅格的空间点格局分析方法无疑比较适合干旱半干旱地区植物空间格局的研究, 在今后一段时间内将会被广泛接受并应用.