文章信息
- 任洪娥, 徐海涛.
- Ren Hong'e, Xu Haitao.
- 细胞特征参数计算机的提取理论
- The Characteristic Parameter Extraction of Cell in Board Assortment Recognition Technology
- 林业科学, 2007, 43(9): 68-73.
- Scientia Silvae Sinicae, 2007, 43(9): 68-73.
-
文章历史
- 收稿日期:2006-09-01
-
作者相关文章
板材是木材工业产品的基本形式,板材价格是家具和建材等行业产品成本构成的主要因素,不同材种的板材价格差别很大。因此,对板材材种的准确鉴别至关重要。然而,现有的人工经验识别法和计算机图像识别法只能在粗略地对板材材种进行识别,对相近材种的识别准确率较低,无法达到令人满意的效果。因此,要想进一步提高板材材种的识别精度,只有更深入地对木材微观构造进行研究(马岩,2002),以木材细胞轮廓提取为研究对象来识别板材的材种(徐海涛等,2005)。
细胞是生物体和生命活动最基本的单元结构,不同木材的细胞体、不同的细胞密度和细胞形状,其木材材性、物理力学性能均不一样(李桂英等,2005)。因此,以细胞的各项特征参数为依据(Callum et al., 1999),对木材的解剖构造特性进行研究,在微观层次上反映木材的宏观特性,成为木材材种识别的重要依据(刘镇波等,2004),也是木材科学研究中的重要研究内容之一(高洁等,2006)。
1 细胞轮廓提取细胞的形态能够较为直接地反映出细胞的各项特征参数,从而为准确、客观地分析细胞特性,进而归纳、预测出木材的材性和材质的优劣提供必要的条件(Gindl et al., 2004)。然而,由于各种原因,细胞的周长、面积等特征参数具有形态不确定的特点,这使得对细胞的形态分析变得困难。如果只是简单地利用细胞呈现出六棱形的规则,将所有细胞都看作六棱形处理,使用特定的多边形周长面积公式求细胞的特征参数误差非常大,不符合实际情况。因此,要精确地计算细胞的面积、周长等参数就要严格地按照细胞真实的形态(细胞的外轮廓)进行统计。这就要求必须准确地找出细胞的轮廓边界,最后利用统计数学求出木材细胞具有统计意义的精确结果。
细胞的边缘轮廓蕴含了丰富的内在信息(如方向、阶跃性、形状等),可以最直接地反映出细胞的形态信息,对特征描述、识别和理解等高层次的处理有着重大的影响。因此,准确地描绘出细胞的轮廓成为细胞形态特征分析的重要线索。
可以使用轮廓提取方法描绘出细胞的边缘轮廓。图像轮廓提取的原理是:假设目标物体内部为黑色,图像的背景为白色。首先遍历图像,如果扫描到的像素点为黑色,并且它的8个相邻点均为黑色,则说明该点是目标物体的内部点,删除该点;否则为边界点,要保留(Rafael et al., 2003)。整幅图像遍历完成后得到的就是目标物体的轮廓。轮廓提取的方法很多,这里只简要介绍以下3种方法。
1.1 差影法差影法实际上是对图像进行代数运算的一种不同的叫法,它的原理非常简单,就是对2幅输入图像进行点对点的加、减、乘、除计算而得到输出图像。加运算:C(x,y)=A(x,y)+B(x,y);乘运算:C(x,y)=A(x,y)×B(x,y);减运算:C(x,y)=A(x,y)-B(x,y);除运算:C (x,y)=A(x,y)÷B(x,y)。
其中差影法的减运算用于获得图像的轮廓。减运算是将前后2幅图像相减得到的差作为结果图像,其目的是为了从图像中去除不需要的信息,只保留所关心的图像信息。
利用差影法的减运算来获得图像的轮廓,具体做法是:首先将原图像二值化,再进行一次全方向腐蚀操作,然后将腐蚀后的图像和二值化后的原图像对应像素点的值相减,最后可以得到目标物体的轮廓。
1.2 模板法用一个一维数组记录目标像素点周围的8个相邻像素点(8邻域像素点)的灰度值。如果8个相邻像素点的灰度值与目标像素点的灰度值均为黑色,则该点在图像的内部,删除这一点;否则保留。依次处理图像中的每一个像素,最后剩下的就是图像的轮廓。
1.3 链码法链码(又称Freeman码)是用曲线起始点的坐标和边界点方向代码描述曲线或边界的方法。在显示器中,目标区域的边界由一系列依次相邻的像素点组成。因此,如果初始点和一系列表示相邻像素间走向的链码(连续值序列)确定了,就可以定义一条基于链码表示的曲线,即链码曲线(罗振东等,1998)。这种表示曲线的方法被称为链码表示法。
算法的右手法则是如果当前像素点有多个相邻点为黑色,那么按着先左邻接点,再上邻接点,最后右邻接点的顺序(对于4方向链码),查找第一个为黑色的点,将该点作为下一个遍历点。轮廓提取过程:首先,开始扫描图像,把扫描到的第一个黑色像素点作为目标物体遍历的起始点,进行边界跟踪;接着,判断当前点的8个邻接方向的像素点,按右手法则找到下一个为黑色的像素点后,将当前点设为访问过状态或直接设置为白色,在链码数组中记录新找到的像素点的链码值;最后把新找到的点设置为当前点,重复上述操作,直到当前点周围8个方向均无黑像素点为止,这时得到的就是目标物体的边界(曹军等,2004)。
上述3种方法均能够实现对目标物体轮廓的准确提取;但链码法具有表示简单、节省存储空间、便于计算以及方向不变性等特点,这为计算细胞的多种特征参数提供了方便条件。因此,本文采用了链码法,处理结果如图 1所示。

|
图 1 链码法细胞轮廓提取 Fig. 1 Cell outline extraction with the chain code method |
细胞轮廓的准确提取为计算细胞周长准备了条件。只要逐点遍历细胞轮廓,计算出轮廓长度就可以实现细胞周长的统计。下面介绍2种求细胞轮廓周长的方法。
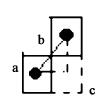
1) 3个相邻像素a、b、c如图 2所示。如果将横、纵向相邻点间的距离长度计为1,即a、c两点是横向相邻,b、c两点是纵向相邻,两点间的距离长度均为1。设斜向相邻a、b间的距离为s,则s2可看作为a、c两点间距离和b、c两点间距离的平方和,所以s=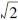
|
图 2 边界点距离计算 Fig. 2 Computation of the boundary point distance |
因此,在细胞的边界像素中,设某像素点与其上下左右像素间的距离为1,与斜方向像素间的距离为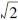
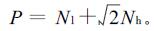
|
(1) |
式中:P为细胞周长;Nl为细胞边界上横、纵向坐标相邻两点构成线段的条数;Nh为细胞边界上斜向相邻的两点构成线段的条数。
2) 将细胞边界上像素点的个数作为周长。其计算公式为

|
(2) |
式中:P为细胞周长;k为细胞边界上像素点的个数。
本文采用方法1)求细胞的周长。对于周长的计算,采用8连通链码法。因为任意一个像素周围都有8个邻接点,8连通链码正好对应这8个点,而4连通链码法由于缺少东南、西南、东北、西北这4个方向,不能有效准确地表示斜方向上的邻接点,在跟踪细胞轮廓时,会造成很大的误差。
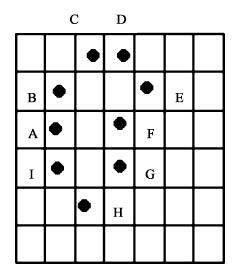
假设图 3中A、B、C、D、E、F、G、H、I为细胞的外边界像素。其中,A、B、I三点和F、G两点的连线是纵向相邻,C、D两点是横向相邻。对于B和C、D和E、E和F、G和H、H和I这些点,两两间构成斜向相邻。这样,图 3中细胞的周长P为:
|
图 3 细胞轮廓图像 Fig. 3 Outline image of the cell |

|
即从起始点A开始,遍历下一个边界点,如果相邻两边界点横坐标或纵坐标相等,则两点间距离值计为1,否则两相邻点距离为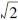
当逐点遍历一个细胞的轮廓计算出该细胞的周长后,表示对此细胞的轮廓遍历结束。此时将细胞计数器的值加1,然后继续寻找图像内下一个细胞进行上述操作。当整幅图像扫描完成后,得到的细胞计数器的值即为图像内细胞的个数(假设图像内没有细胞粘连情况)。
2.3 细胞面积计算2种求细胞面积的方法:
1) 在二值图像中,封闭区域是由相互连接在一起的多个黑像素的集合构成的一个黑色区域,所以在这个封闭区域内的像素点的个数即构成了封闭区域的面积(以像素点为单位),在这里可以把细胞看作封闭区域,从而计算细胞的面积。其计算公式为
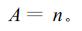
|
(3) |
式中:A为细胞面积;n为细胞内像素点的个数。
2) 采用链码表进行细胞的面积统计。将细胞区域看成由多条水平线组成,每一条线段可以用该线段的2个端点表示,如图 4所示。可以将目标物体看成是由很多条紧密相邻的水平线段组成。这样,区域内所有水平线段的长度和就是目标区域的面积。具体做法是:根据链表中记录的链码值计算出各边界点的坐标,然后找出具有相同纵坐标的点,作为线段的左右端点,计算2点间横坐标的差即线段长度,这样区域内所有线段的长度和就是该细胞的面积。其计算公式为
|
图 4 线段表表示法 Fig. 4 Method of the line segment table denotation |

|
(4) |
式中:A为细胞面积;xk1、xk2分别为线段左、右端点的横坐标;k为线段的标示变量;m为线段的条数。本文应用该方法进行面积的测量。
2.4 圆形度计算在求出细胞的周长和面积后,可以很方便地求出细胞圆形度。圆形度用来描述图形和圆的近似程度,其值越接近于1,就越接近于圆形。其计算公式为

|
(5) |
式中:C为细胞的圆形度;P为细胞的周长;A为细胞的面积。
2.5 重心计算求细胞(对于任意封闭区域也适用)重心的方法和面积计算中的方法1)相似。将目标物体看成由多条紧密相邻的水平线段构成。首先根据链码表中的链码值计算出各个边界点的坐标,然后找到边界点中纵坐标相同的点,作为线段的左右端点。找到端点后,计算X和Y方向的矩。X方向矩等于线段两端点的横坐标的中值乘以该线段的长度值,Y方向矩等于线段的长度乘以端点的纵坐标(因为水平线段两端点的纵坐标相等)。通过上述方法求出了一条线段的X、Y方向的矩,将目标区域内所有线段的X、Y方向的矩相加,最后平均(除以各线段的长度累加和即面积)就得到了细胞重心的X、Y坐标。注意这里的线段长度以像素为单位,所以在利用线段两端点的横坐标之差表示线段长度时还应该加1。其计算公式为
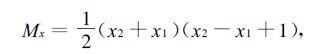
|
(6) |
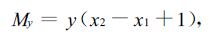
|
(7) |
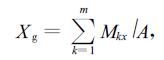
|
(8) |
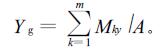
|
(9) |
式中:Mx、My分别为线段的X、Y方向的矩;x1、x2分别为线段左、右端点的横坐标;y为线段左右端点的纵坐标;Xg、Yg分别为细胞重心的X、Y坐标;A为细胞面积;Mkx、Mky分别为第k条线段的X、Y方向的矩;m为线段的条数。
3 参数提取理论的实际应用 3.1 计算机标示量与实际细胞尺寸的转换通过以上各算法,可以得到木材细胞的周长和面积等参数,但这些参数是在计算机显示器上以像素为单位表示的。要想获得实际的细胞参数值,还要进行由像素到实际细胞参数值的换算。其计算公式为
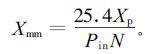
|
(10) |
式中:Xmm、XP分别为实际细胞参数值和计算机上显示的细胞参数值;Pin为计算机显示器上每毫米长度所含的像素点个数;N为细胞图像放大倍数。
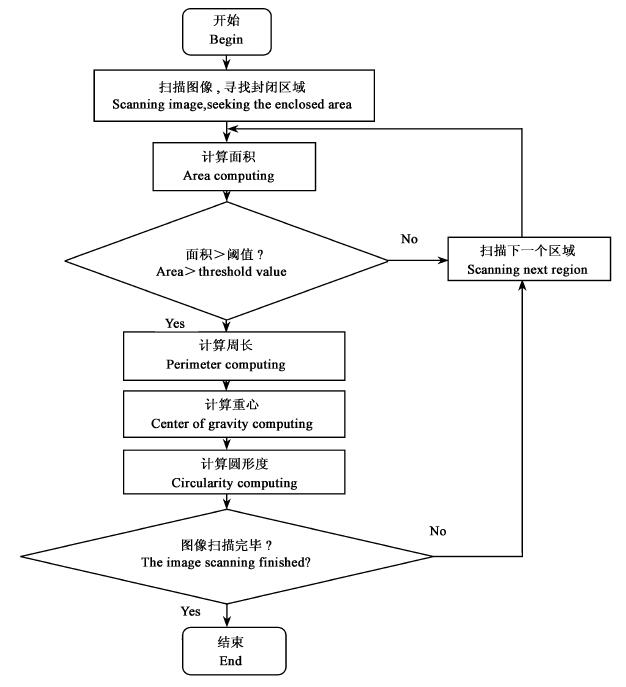
3.2 参数计算流程假设进行细胞各参数统计时,图像已处理为黑白二值图像,且细胞为黑色,背景为白色,则统计细胞各项参数的具体流程是:首先扫描整幅图像,计算扫描到的第一个封闭区域的面积。如果该区域面积值小于规定阈值,则视为扫描到是无统计意义的区域,不计算其参数,直接扫描下一个封闭区域;否则扫描到的是细胞,继续计算细胞的周长、重心、圆形度。计算完毕后,再扫描下一个封闭区域重复上述操作,直到整幅图像扫描完毕,程序结束。其流程图如图 5所示。
|
图 5 参数计算流程图 Fig. 5 Flow chart of the parameter computing |
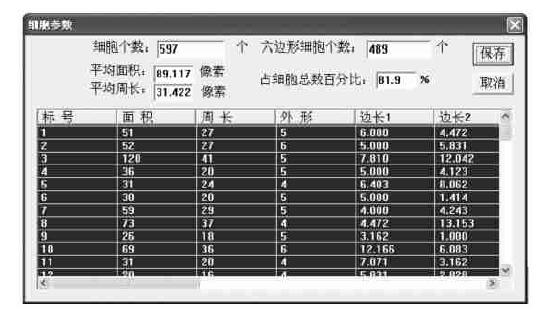
在10块落叶松(Larix gmelinii)细胞照片上各选6~12个样本,使用北京天地科技有限责任公司的木材显微图像分析软件和本文提出的细胞特征参数测量方法(使用面向对象的程序设计语言Microsoft Visual C++实现)对样本细胞图像进行面积、周长测量。以图 6所示落叶松细胞样本的图像分析为例,图 7是本文软件对图 6所示样本图像分析结果。

|
图 6 落叶松细胞图像 Fig. 6 Cell image of larch |
|
图 7 本文软件分析结果 Fig. 7 Analyzing result from the software in this article |
本文编制的软件与北京天地公司的软件对图 6落叶松细胞图像进行测量的结果如表 1所示。2个软件测量结果比较的细胞平均面积误差小于万分之一,细胞计数误差和面积测量误差是由于2个软件对图像边缘和不完整细胞的处理方法不同造成的,平均周长的误差也是由二者计算方法不同引起的。可见,本文提出的木材细胞特征参数测量方法是实用、可行的。
|
|
木材细胞的周长、面积、个数等特征参数,对于从微观领域对木材的宏观特性做出预测和分析,提高板材材种的识别精度有着重要意义。基于链码的木材细胞特征参数的提取方法具有提取细胞轮廓方法精确、简单,节省存储空间,计算速度快等优点,从而为板材材种的准确识别提供了有效的方法。
本文提出的参数计算方法丰富了木材细胞的统计数学分析理论,为计算机自动分析木材细胞提供了理论和方法。
曹军, 张冬妍. 2004. 形态特征及神经网络在木材横纹压缩中的应用研究. 计算机应用研究, 21(6): 44-46. DOI:10.3969/j.issn.1001-3695.2004.06.015 |
高洁, 任洪娥, 马岩. 2006. 基于细胞数字特征的板材材种识别技术. 林业机械与木工设备, 34(1): 39-41. DOI:10.3969/j.issn.2095-2953.2006.01.013 |
李桂英, 刁宏志. 2005. 计算机在木材细胞数字化理论中的应用. 林业机械与木工设备, 33(1): 22-24. DOI:10.3969/j.issn.2095-2953.2005.01.006 |
刘镇波, 刘一星, 于海鹏. 2004. 基于量化构造特征参数的树种计算机识别算法. 福建林学院学报, 24(3): 265-269. DOI:10.3969/j.issn.1001-389X.2004.03.018 |
陆宗骐. 2005. C/C++图像处理编程. 北京: 清华大学出版社, 277-294.
|
罗振东, 廖光裕. 1998. 计算机图形学原理和方法. 上海: 复旦大学出版社, 44-53.
|
马岩. 2002. 木材横断面细胞结构的数学模拟理论研究. 生物数学学报, 17(1): 64-68. DOI:10.3969/j.issn.1001-9626.2002.01.011 |
徐海涛, 任洪娥, 马岩. 2005. 板材材种识别中计算机图像处理技术的应用. 木材加工机械, 16(6): 32-33. DOI:10.3969/j.issn.1001-036X.2005.06.010 |
Callum A S., Dennis J. 1999. Dimensional changes in Corisian Pine sapwood due to chemical modification with linear chain anhydrides. Holzforschung, 53(3): 267-271. DOI:10.1515/HF.1999.045 |
Gindl W, Gupta H S, Schöberl T. 2004. Mechanical properties of spruce wood cell walls by nanoindentation. Applied Physics A-Materials Science & Processing, 79(8): 2069-2073. |
Rafael C G, Richard E W. 2003. Digital image processing. Second edition. 北京: 电子工业出版社.
|
 2007, Vol. 43
2007, Vol. 43

