在林业经营管理中，林木蓄积估测是一项重要而复杂的工作。传统的做法是对标准地进行调查，以标准木平均胸径、树高进行估测，人为影响较大。近年来，随着计算机的普及和人们认识问题的不断深化，有着丰富理论基础的线性模型得以广泛应用于林业、农业、生物和经济等各个领域(蔡体久等，2003；2005；Baker et al.，2004；李崇贵等，2001a; 2001b；张焱，1999)，为科学研究由定性描述转向定量评价提供了坚实的基础。特别是如何通过遥感技术，结合少量地面调查资料，估测森林蓄积甚至碳储量成为人们研究的热点。由于不同领域事物本身的复杂性，一种结果的产生往往是由不同的因素直接或间接导致的，人们囿于知识和经验的不足，有时候并不能确定它们之间的线性关系是否成立(Bennett et al.，2004；王松桂等，2004)。而神经网络技术是模拟人脑生物过程的智能系统，在研究复杂系统内部相互关系及建模方面有其独特的优越性，它最大的特点在于具有学习能力，通过各种学习算法来调整网络中的权值和阈值，使相似的输入有相似的输出。目前，神经网络技术用于森林蓄积估测的报道很少(李际平等，2001；邓立斌等，2002)，本文基于MATLAB6.5，通过实例比较了普通BP神经网络与经规则化调整法进行泛化改进的BP神经网络(简称泛化BP神经网络)预报森林蓄积精度的差异，并试验了将原变量进行主成分变换，以主成分得分为输入参数训练网络和仿真对蓄积预报的影响，最后用泛化BP神经网络进行仿真计算，很好地估测了试验样地的森林蓄积量。

1 材料与方法 1.1 数据获取与处理

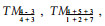
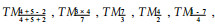
试验在云南思茅地区，共选取129个森林资源一类清查固定样地所对应的遥感图像6个波段灰度值和相应的一类调查资料中的高程、有林地、阴坡、阳坡、郁闭度等5个GIS信息数据，并构造遥感比值波段如下(Murakami, 2004；赵宪文等，2001；蔡体久等，2003；2005；李崇贵等，2001a；2001b)：即共用18个变量估测森林蓄积量。将这129个样地的观测值按行排列构造数据矩阵(129×18)，用80个样地数据建立蓄积估测模型，剩余的49个样地数据进行预报检验。

为消除遥感因子与GIS因子量纲不同的影响，先将所有这129个样地的观测数据矩阵按列进行中心标准化，即每一个变量观测值减去变量序列的均值然后除以此变量序列的标准差(张焱，1999)

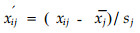
(1)

式中：x_ij^′为中心标准化观测值，x_ij为原始观测值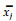，为第j变量的均值，s_j为第j变量的标准差。

在MATLAB中，内嵌函数prestd()可以实现这一运算。具体计算时，参数X是观测值矩阵的转置矩阵。函数返回值根据输入参数的个数不同而有差别，实际应用时可以参阅MATLAB的帮助文档。

1.2 主成分变换

由于在选择设置影响蓄积估测的变量时，往往难以确定哪些变量与蓄积显著相关以及变量之间是否也存在相关性，于是总是希望选择尽可能多的变量构造方程，结果带来了新的问题。变量多不仅增加了计算时间，而且变量之间可能存在的相关性使得回归模型不尽人意(李崇贵等，2001a；2001b；蔡体久等，2003；2005)。而主成分变换通过构造由原来变量特殊线性组合(以协方差阵的特征向量为系数)而成的新变量，不仅使生成的变量是线性无关的，且集中了原有变量的主要变异信息，可以在保证足够精度的前提下减少变量向量的维数(王松桂等，2004；Garey，2005；杨荣英等，2002；孟明等，2004)，提高估测模型的运算速度。

主成分变换方法在MATLAB神经网络工具箱也有描述，可以利用函数prepca(P, minfrac)返回特征向量矩阵和主成分得分矩阵。其中：输入参数P为中心标准化的观测阵，minfrac是阈值，表示主成分方差贡献率不足此数值时不参与计算。

1.3 泛化BP神经网络仿真建模

在BP神经网络的训练算法中，都是通过计算性能函数的梯度，再沿负梯度方向调整网络的权值和阈值，从而使性能函数达到最小。普通BP神经网络都采用网络训练误差的平方和均值即均方误差作为性能函数，公式为

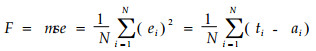
(2)

式中：e_i、t_i和a_i分别表示第i个样本的训练误差、目标输出和网络输出。

这种普通BP网络记忆已被训练的样本，对新的输入没有良好的泛化能力，使得网络对新输入的输出与对应的目标输出之间有较大的误差，影响模型预报精度。为了提高神经网络的泛化能力，MATLAB神经网络工具箱提供了2种方法，本文采用规则化调整方法，即通过调整网络的性能函数来增强网络泛化能力。调整后的网络性能函数为

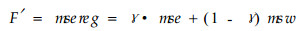
(3)

其中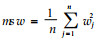：, γ是性能参数，w_j是网络权值。

使用该性能函数可以减少网络的有效权值和阈值，使网络的训练输出更加平滑。在MATLAB中，函数trainbr把网络的权值和阈值看作是特殊分布的随机变量，用最大似然估计理论自动设置最优性能参数，实现网络泛化能力的提高。本文用式(4)创建神经网络，用中心标准化的80个样地数据训练它(式(5))，把剩余49个中心标准化的样地数据与训练过的神经网络一起作为参数进行仿真输出(式(6))，将网络的输出output做中心标准化的逆变换，即为蓄积观测值的预报值。

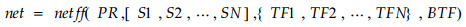
(4)

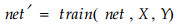
(5)

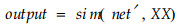
(6)

其中：输入参数PR为输入向量的取值范围，Si为第i层神经元的个数，TFi为第i层的传递函数(文中取tansig和purelin)，BTF为网络训练函数；X为数据矩阵，Y为目标(理想)输出，XX为用于仿真预报的数据矩阵(闻新等，2003；Demuth et al.，2002；杨荣英等，2002；孟明等，2004)。

2 结果与分析 2.1 神经元传递函数的选择对网络仿真的性能影响

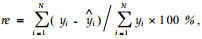
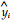
MATLAB神经网络工具箱给出了BP神经元的3个传递函数：对数S形函数(logsig)、正切S形函数(tansig)和线性函数(purelin)，采用不同的传递函数将得到不同的输出结果。创建只有输入层和输出层的单层神经元BP神经网络，以中心标准化的80个样地数据做为输入数据，用训练函数trainlm比较3个传递函数对网络性能的影响，结果如表 1。估测值相对误差按下式计算：其中:re是所有样地蓄积估测值相对误差；y_i是实测值，网络的目标输出；是网络的实际输出；N是预报样地个数。

从表 1可以看出，采用单层BP网络时，以线性函数作为传递函数，网络训练只需4次就收敛了。进行蓄积量仿真预报计算，比用其他传递函数具有更高的精度。

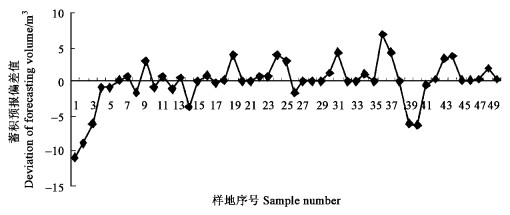
2.2 普通与泛化BP神经网络的性能比较

创建单层普通(训练函数为trainlm)和泛化(训练函数为trainbr)BP神经网络，以线性函数作为神经元传递函数，以中心标准化的80个样地数据作为输入数据进行网络训练，用剩余的49个样地进行蓄积量仿真计算，计算偏差见图 1，并比较2个模型的性能指标，结果如表 2所示。可以看出，泛化BP神经网络同普通BP神经网络相比，虽然训练次数增多了，但整个计算所耗时间在减少，并且用泛化BP神经网络仿真计算预报的蓄积量具有更高的相对精度。

2.3 PCA处理对网络仿真的影响

将中心标准化的观测值进行主成分分析(PCA)，以累计方差贡献率不小于98%的主成分得分作为单层泛化BP神经网络的输入数据进行网络训练与仿真计算。结果表明：以主成分得分作为输入数据，确实可以更快地使网络趋于收敛，但要损失一部分精度(表 3)。

2.4 隐含层神经元个数对网络仿真的影响

BP神经网络经常具有多层结构，除了输入层和输出层，中间的部分称之为隐含层，隐含层神经元常用S形传递函数，输出层则用线性传递函数。本文将80个样地观测值主成分得分作为输入数据，用tansig作为隐含层神经元传递函数，试验了1、3、5、10个神经元对模型精度的影响。结果发现：3个神经元时的估测精度最好，再增加神经元的个数并不能显著提高模型仿真估测精度(表 4)。

3 结论与讨论

1) 以普通BP神经网络进行森林蓄积量仿真预报，预报值与实测值的误差较大，经泛化改进的BP神经网络森林蓄积量预报值与实测值的误差较小，这一点在具有隐含层网络结构的仿真模型中体现地更明显。

2) 就本文绝大部分样地而言，用泛化BP神经网络仿真计算的蓄积预报值与实测值相差较小(图 1)；单层泛化BP神经网络比多层网络具有更高的整体仿真预报精度，所有预报样地总蓄积量的相对预报精度达99%。如何在保证模型整体仿真预报精度的前提下提高单个样地的估测精度仍需进一步研究。

3) 以主成分分析方法简化输入数据，可以使神经网络更快地趋于收敛，在保证一定精度的前提下极大提高运算效率，数据量越大越明显。

4) 是使用单层还是具有隐含层的多层BP神经网络进行网络训练与仿真计算，神经元的个数多少，应该视具体的任务而确定，其原则是：在网络训练精度一致的情况下，使仿真模型具有更高的预报精度。

本文进行网络训练与仿真时，数量化数据(只有0和1两个数值)与实测数据未区别对待，但将定性数据数量化后与任取实数值的观测值混合构造观测阵建立回归模型，与对混合观测阵进行分块处理再建立回归模型，是否会得到一致的结果，是今后工作中需要进一步研究的问题。