分形几何学(fractal geometry)理论(Mandelbrot，1982)，是美国著名数学家Mande lbrot在前人研究基础上丰富和发展起来的。它最初源于对难以用欧氏整数维数学来描述的，介于点(0维)与线(1维)、线与面(2维)、面与体(3维)等体系间的不规则几何体的刻划与描述。树体的分枝结构和树冠的形体结构都是较为典型的分数维体，难以用经典(欧氏)几何学对其进行准确的描述和定量分析(叶万辉，1993)。勿庸置疑，分形几何理论与方法是树体结构分析最有效的研究手段之一。Zeide基于计盒维度的原理，提出了测度树冠表面积分数维度的有效方法，即“双表面积法”和“双数量法”(Zeide，1990；1991)；叶万辉(1995)用Zeide方法，以分数维度为基础，对胡桃楸(Juglans mandshurica)、水曲柳(Fraxin us mandshurica)和黄菠萝(Phellodendron amurense)树冠最佳结构理论进行了初步探讨。

单木是林带的基本组成单位，其结构是林带结构研究的最基本层次，林带中单株树冠结构对林带整体结构有着重要的影响。单株树木间的相互作用及其与环境的适应过程就构成了林带结构整体的变化机制(李春平等，2003)。透光疏透度仅是对林带纵断面平面形状的反映(2维指标)，因此，曹新荪(1983)提出了比较精确地描述林带结构的立木疏透度(3维指标)，但是由于没有适宜的、简捷的定量测度方法，在实践中未能得到广泛应用。周新华等对林带的三维动力结构进行了研究，提出植物表面积密度和立体密度作为描述三维动力结构的指标，并建立了两项指标的模型(Zhou et al., 2002；2005)。因此，从三维角度探寻更精确地描述林带结构的指标，是林带合理结构研究的重要问题。本文从分维角度细致解析林带小钻杨(Populus×xiaozhuanica)树冠的分维结构，为进一步林带分形维数测算提供依据，以指导农田防护林的经营与管理。

1 材料与方法

辽宁省昌图县双井子镇(123°32′ —124°26′ E，42°33′ —43°29′ N)地处科尔沁沙地的东南边缘，明显的大陆性气候特点，年均气温6.7 ℃，≥10 ℃积温为3 259 ℃，平均风速4.5 m·s^-1，≥8级大风日76 d。土壤为草甸棕壤，质地较粘重但肥力较高，主要自然灾害为风害。研究对象的农田防护林是中国科学院沈阳应用生态研究所“三北”地区农田防护林研究基地试验林，基地营建了多种混交方式、多种配置、多种更新改造类型、不同年龄时段的农田防护林，是开展农田防护林林带结构研究的理想试验基地(范志平等，2001；关文彬等，2002)。

1.1 分数维度计算方法

分数维度是定量描述分形特征的参数，分形维数的定义有很多种，且对同一物体以不同方式定义或侧重面不同，其分形维数也各不相同。计盒维数反映的是分形体对空间的占据程度或种群利用生态空间的能力(马克明等，2000)。本文用盒子计数法来统计小钻杨分枝的分形结构，其计盒维数D′(肯尼思，1991)采用下式计算：

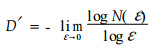
(1)

在实际应用中，一般不求算当ε→0时的极限值，而是在双对数坐标下，对上面获得的一系列成对的非空格子数N(ε)和格子边长(ε)进行线性回归，所得拟合直线斜率的绝对值即是计盒维数的近似估计。

树冠分数维度(D_c)是叶片对树冠空间填充程度的表征，其D_c值的计算采用双数量法：

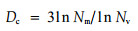
(2)

式中：N_m=W_LS/w_l, N_v=V_S/v_s, W_LS为全部叶生物量，V_S为树冠总体积，w_l为某一枝条的叶生物量，v_s为枝外壳的体积。

Zeide在提出双表面法的同时，提出了判定树冠是否具有分数维度的关系式，树冠体积V_S与W_LS叶生物量间的相互关系式：

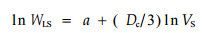
(3)

导出：

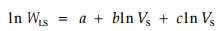
(4)

式中:a、b、c均为常数。当该方程为线性时，即c→0时，树冠就具有结构上的自相似性(Zeide，1991)。

1.2 生物量模型

在目前标准的树木或林分生物量研究中，人们多以相对生长(relative growth)概念(Huxley et al., 1936)为基础，对这一关系进行分析和讨论(Lieth et al., 1975)。本研究对样木的干、枝、叶的生物量与测树因子的实测数据作了回归分析，应用以下4种模型进行研究：

复合因子幂函数回归法

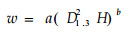
(5)

胸径幂函数曲线回归法：

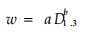
(6)

指数回归法：

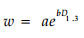
(7)

直线回归法：

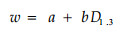
(8)

2 结果与分析 2.1 树冠结构的模拟

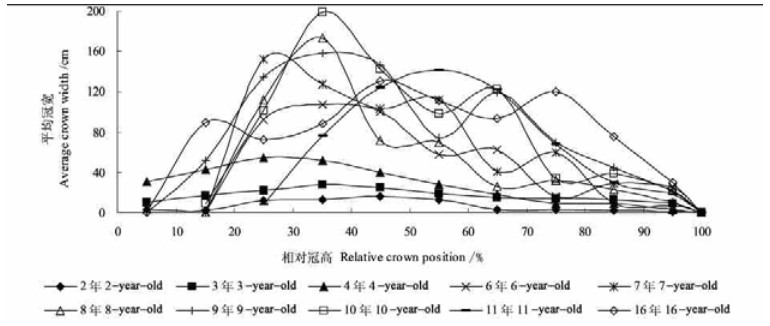
应用双数量法对树冠表面分数维度进行计算时，必须计算出树冠的体积。本文统计得到各树龄树冠不同相对冠高层次的垂直变化特征(图 1)，分析不同年龄个体间树冠的变异。

从图 1中可以看出，不同年龄个体的冠形存在差异，但是树冠最宽处基本上都处于中下部。6年生以上小钻杨冠宽变化明显，而6年以下的冠宽变化较缓。原因在于：6年生以上的林带基本上达到郁闭状态，在最大冠宽处以下，受光渐弱，但是，在试验基地中，所有的防护林木均经过修枝，在枝下高以下有相对较多的光热空间。因此，最大冠宽处以下的侧枝不再向上方竞争，多向斜下方低垂。边行外侧冠形发展的光照空间较充分，但受两侧平均趋势影响，趋势与内侧相一致。6年生以下的小钻杨林带未达到郁闭状态，树木外部光照均衡，因此冠宽变化不明显。

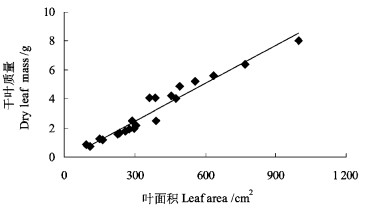
2.2 树冠特征统计分析 2.2.1 干叶质量与叶面积的关系

通过对标准叶面积和其相对应干叶质量关系的回归分析(图 2)，可知2者存在极显著线性关系，线性关系式为y=0.008 8x-0.149 6，相关系数r=0.971 0, 检验值r_0.01=0.536 8。

2.2.2 树冠体积与叶生物量的关系

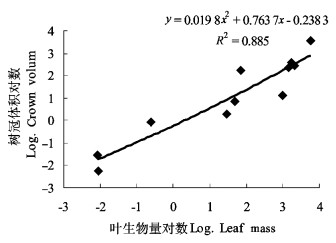
依据树体整体叶生物量和体积之间的对数式(4)来判断叶生物量与树冠的相似性。结果如图 3所示，各年龄平均标准木的树冠体积V_S与叶生物量W_LS之间呈极显著的多项式回归关系：r_0.01(10)=0.707 9，其二次项的系数为0.019 8，小于0.05，表明叶与树冠结构具有相似性。同时，我们还用同样的方法对侧枝生物量和树冠体积，及总生物量和树冠体积做对数式拟合，结果表明均存在着结构的自相似性。

因而，可用树冠整体叶生物量与一级分枝叶生物量之间的比率来求算树冠分数维度。对于每个枝条，确定它的叶生物量(m_l)和其外壳的体积v_s，通过对枝条和树冠之间叶生物量和体积的比率，得N_m=M_LS/m_l和N_v=V_S/v_s。利用公式(3)，直接由单个枝条测定树冠分数维度，但实际应用中，必须对许多不同大小的枝条进行测定，对lnN m和lnN_v进行回归，来确定树冠分数维度。

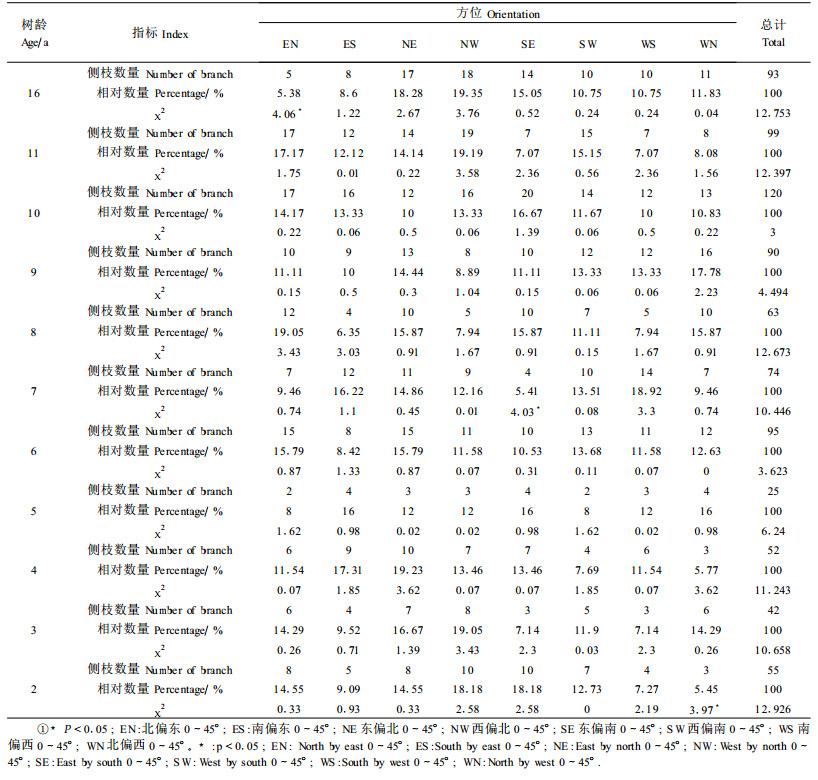
2.3 侧枝及倾角分布规律 2.3.1 侧枝分布规律

对不同年龄样木的侧枝数量、长度、倾斜角度、着生部位高度及其在8个方位上的数量分布进行测量。通过统计各个方位的侧枝数量，得到各年龄树的侧枝方位分布状态(表 1)。表中所列的χ²值为利用假定：χ²=(实测值-理论值)²/理论值。假定各侧枝在每个方位上均匀分布，在各方位出现枝数的概率即为理论频数(其值为12.5)。在每个方位上如果χ²>χ_0.05²=3.814时，则认为差异显著；而总体χ²(7)>14.067时，则认为侧枝在各方位上的分布是不均匀的。通过实测检验，不同年龄的小钻杨在各方位上均符合均匀分布；从不同年龄样木分枝的总体来看，也符合均匀分布。

2.3.2 侧枝倾角分布规律

将所测得的各树龄样木的侧枝倾角，即侧枝在树干上的着生角度(所测得的最大角度值为120 °)，按每15°为1个角度级划分，把0~120°分成8个角度级，分别用1~8的数字表示，结果显示各年龄小钻杨的侧枝分枝角度均较集中，随着年龄的增长，角度级在逐渐加大。这也说明随着年龄增长，枝的向上生长势减弱。对各年龄小钻杨的侧枝倾角进行正态分布检验得表 2，临界值均为χ_0.05²(5)=11.07，所有的检验值都小于临界值，由此可知各年龄小钻杨侧枝倾角在各角度级中的分布均服从正态分布。

2.3.3 侧枝在树冠内的分布格局

枝条和叶片形成的分枝格局是树冠的构成单元，对其进行定量化描述，对于我们研究树冠结构特征具有重要意义。分枝的分形格局通过盒子计数法来统计。

从表 3中可以看出各树龄样木的计盒维数平均值为1.641，相关系数均达0.99以上，标准差为0.184。尽管各树龄样木的树冠体积与生物量均有差异，但其计盒维数没有显著差异。证明小钻杨树冠分枝格局的分形维数独立于尺度，正好刻画了各枝条分枝格局的自相似性，具有比较典型的分形特征。经研究表明，兴安落叶松(Larix gmelinii)分形维数为1.4~1.7(马克明等，2000)，红树植物木榄(Bruguiera gym norhiza)枝条的计盒维数为1.22~1.55(梁士楚等，2002)，小钻杨枝条的分形维数较高，揭示出其分枝结构十分复杂。

2.4 生物量模型

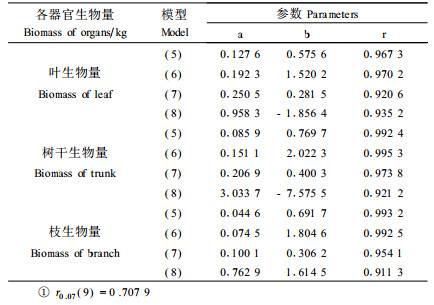
分别用公式(5)~(8)模拟生物量和，结果见表 4，用公式(5)和(6)模拟都有极显著的相关水平，但(5)比(6)含有更多的相关信息，因此，本研究选用公式(5)复合因子幂函数回归模型来计算各器官的生物量。

2.5 树冠分数维度

用叶生物量、枝生物量、总生物量以及公式(2)，求得各年龄林木的树冠分数维度(表 5)。从表 5可以看出有叶期的分数维度值为2.065~2.765，无叶期的分数维度值为2.003~2.464，有叶期的分数维度值大于无叶期。同时随年龄的变化树冠分数维度值呈现出先增大后减小的趋势。用Zeide的算法计算木榄树冠分数维度值为2.21~2.54，随年龄增加分数维度值减小(梁士楚等，2002)。落叶树种通常分为有叶期和无叶期, 而Zeide的算法，只考虑了有叶期的树冠分数维度的计算。本研究用枝生物量代替叶生物量测定树冠分数维度，丰富了Zeide的分维度计算方法，为无叶期林冠结构的研究提供了方法。

2.6 基于分数维度的最佳树冠结构的探讨 2.6.1 不同树冠体积和叶生物量下的树冠表面分数维度

由树冠内叶生物量W_SL与树冠体积V_C 的相互关系方程(3)可知，树冠表面积分数维度受树冠内叶生物量与树冠体积的双重影响：树冠体积相同时，叶生物量越大，分数维度越大，树冠受光表面积也就越大；相反，在同等叶生物量时，树冠体积越大，树冠分数维度越小，树冠受光表面积也越小。本文与叶万辉(1995)的结论一致。

为探寻树冠体积与叶生物量变化对树冠分数维度的影响，假定各个树冠体积和叶生物量等级，应用公式(3)对分数维度值进行计算。共设定14个树冠体积等级，分为0.1、5、10、15、25、30、40、60、80、100、150、200、250、300 m³；叶生物量分为0.1、1、5、10、15、20、25、30、35、40、45、50、55、60、65、70、75、80、100、120、150、200、250、300 kg，共24个等级，计算结果如图 4。

同一叶生物量等级，填充不同体积的冠层，其树冠表面积结构明显不同，如叶生物量为15 kg, 冠层体积在15、25、30、40、60 m³ 5个等级上，可以保证树冠形成与体积相匹配的合理表面积，其分数维度值为3.171~2.097；而不同叶生物量等级，填充相同的冠层体积，其树冠表面积结构也明显不同，如冠层体积为60 m³时，叶生物量为15~55 kg, 可以保证树冠形成与体积相匹配的合理表面积，其分数维度值为2.097~3.049。根据分形体的表面积和体积的维度关系可以确定：叶生物量与树冠形成比较合理的树冠结构时，其树冠表面积分数维度值为2.0~3.0。

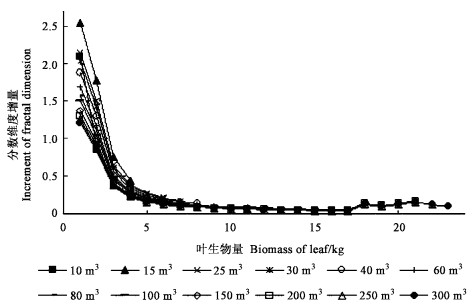
2.6.2 树冠表面分数维度值的变化与叶生物量增加的关系

根据计算叶生物量等级间分数维度增量的公式ΔD_c=D_W0-D_W1(W₀为现等级叶生物量，W₁为叶生物量增加前的等级) (叶万辉，1995)，求算出不同冠层体积由于叶生物量变化导致的分数维度变化值，分数维度增量的变化值如图 5。

由图 4和5可以看出，树冠体积不同时，分数维度的绝对值和相对值变化规律基本一致，在叶生物量小时，随着叶生物量增加，分数维度值有明显的增加，当叶生物量达到一定数值后，叶生物量的增加对其值的影响便逐渐减弱。不同体积的树冠均需要一个基本的叶生物量维持其表面积，当叶生物量超过最佳值后，分数维度就不会有明显的变化。

3 结论

1) 各年龄的小钻杨侧枝在各方位上服从均匀分布，侧枝倾角在各角度级上服从正态分布。

2) 小钻杨树冠分枝格局的分形维数独立于尺度，具有比较典型的分形特征，其计盒维数值为1.510~1.733，分形维数越高，其分枝结构越复杂，其占据和利用生态空间的能力越强。

3) 小钻杨个体树冠具有自相似性，可用分形维数来刻画其结构特征，以叶生物量为基础的树冠分数维度值为2.065~2.765；应用双数量法，用枝生物量代替叶生物量，计算小钻杨无叶期树冠分数维度值为2.003~2.464。这种以枝生物量为基础的树冠分数维度测算，为无叶期林冠结构的研究提供了方法，丰富了Zeide的分维度计算方法。

4) 树冠表面积分数维度受叶生物量与树冠体积的影响，不同树冠体积条件下，分数维度绝对值和相对值的变化规律基本一致，且随着叶生物量的增加，差异逐渐减小。在树冠的构成上，不同体积均有一个基本的叶生物量维持其表面积，也有一个最佳值，即超过这个最佳值，树冠分数维度值不再有明显变化。