文章信息
- 胡蕙露, 蔡新玲.
- Hu Huilu, Cai Xinling.
- 均匀设计优化银杏培养基配比
- Optimization of Medium Proportion of Ginkgo biloba by Uniform Design
- 林业科学, 2006, 42(10): 39-42.
- Scientia Silvae Sinicae, 2006, 42(10): 39-42.
-
文章历史
- 收稿日期:2005-08-15
-
作者相关文章
银杏(Ginkgo biloba)为我国独存的珍稀名贵树种, 其种子、叶片富含多种化学成分, 可入药。大面积栽种银杏会占用许多土地, 同时银杏叶的生长及叶中的黄酮的含量会受到自然环境的影响。完善的繁殖技术一直是制约银杏推广的巨大障碍; 利用组织培养技术来改善它的繁殖方法, 在生产上显示出很大的优点。采用均匀设计表来设计银杏等组织培养中激素的配比, 未见到相关报道。均匀设计(uniform design)是方开泰等(方开泰等, 1994; 2001;Fang et al., 1994; 2000;Fang, 2002)为了解决多因素、多水平高科技难题而提出的一种试验设计。基于试验点在整个试验范围内是均匀散布的, 从均匀性角度出发, 大大减少了试验次数, 并且分析准确性好; 能从全面试验点中挑选出部分代表性的试验点, 这些试验点在试验范围内充分均衡分散, 但仍能反映体系的主要特征。它与其他试验设计法的最大不同之处就在于能从尽可能少的试验次数中揭示出因素对指标的影响大小和规律; 能够以最少的次数, 从多个因素中找出影响试验结果的各因素的主次和最优结果; 并且可以进行优化拟合设计。
张瑛均匀设计网(2004)详细介绍了均匀设计理论和大事记, 如1978年在实际问题的推动下, 中国科学院数学所王元和方开泰提出了“均匀设计”的理论并计算出一批均匀设计表。1979年按照均匀设计理论和方法, 赵利华、王济成等分别给出了3种型号的指挥仪数学模型中弹道坐标的2种形式的回归关系式。这是均匀设计在电脑仿真试验中的3项先驱的应用。1983年, 纺织学报发表张季伦和王晓琪的论文“均匀设计在纺织工业中的应用”。随后, 均匀设计相继在医药、石油、化工、轻工、军工、治金等几十个大中型企业进行应用推广, 效果卓著。
1 材料和方法 1.1 试验材料试验材料包括幼叶、茎段和芽, 均采自安徽农业大学校园内。幼叶取于2004年3月份, 4月中旬选生长旺盛的银杏多年生植株取其当年生幼嫩的茎段及其萌芽作为外植体。
1.2 培养基采用MS培养基, 附加不同浓度的植物生长调节剂6-BA、2, 4-D、NAA, 按试验方案组合成不同配比。
1.3 试验方法培养基配制 包括基本培养基母液配制、各组合培养基制备及分装、高压灭菌及消毒。
新材料消毒 常规消毒:70%酒精30 s, 后用0.1%的升汞浸泡10 min, 其中加入1~2滴表面活性剂吐温; 在无菌条件下将外植体切成一定大小, 转入消毒过的培养皿中备用。
外植体接种 在超净工作台上进行无菌操作。
继代增殖循环 第1次接种并诱导成功的材料在若干天后分别转移到同样的培养基中进行继代培养, 每过半个月继代1次。
1.4 试验设计及统计方法采用的是方开泰(1994)利用数论方法设计的各种均匀设计表; 并采用王玉方(2003)试验设计与参数优化软件注册版进行统计分析。
1.5 试验过程采用王玉方(2003)均匀设计软件程序进行试验设计与数据分析, 按照如下步骤进行:
1) 设置因素数 以不同的植物生长调节剂作为试验因素, 包括NAA、2, 4-D、6-BA (单位为mg·L-1), 把不同外植体也作为1个因素数, 共设置因素数为4个。
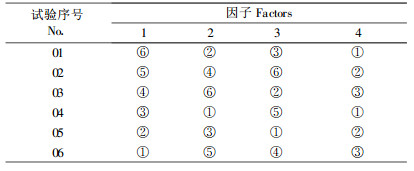
2) 设置试验数 设置不同水平试验, 其中NAA、6-BA、2, 4-D各6个水平, 外植体为3个水平, 共设置了6组试验数。根据均匀设计表U4* (64)得表 1, 因素水平组合为6×6×6×3。
|
|
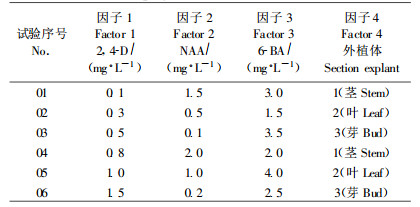
3) 建立试验方案 试验方案见表 2, 其中NAA浓度为2.0, 1.5, 1.0, 0.5, 0.2, 0.1 mg·L-1共6个水平, 6-BA为4.0, 3.5, 3.0, 2.5, 2.0, 1.5 mg·L-1共6个水平, 2, 4-D为1.5, 1.0, 0.8, 0.5, 0.3, 0.1 mg·L-1共6个水平, 部位3个水平, 分别为茎段、叶、芽。
|
|
4) 按试验方案进行试验 建立试验方案后, 按试验方案进行试验。观察试验结果, 对不同部位外植体培养的结果进行观察、记录, 取其平均数进行数据分析。
5) 多元线性回归模型建立 根据专业知识判断建立线性回归模型。若选择线性模型则应清除二次项、三次项、交互项设置区中的设置。
6) 设置显著性检验水平 包括回归模型有效性检验和回归方程中各方程项对回归显著性的检验; 两者使用同一显著性检验水平设置值。
7) 执行多元回归分析 检验回归模型是否有效并反复进行回归模型拟定(在专业知识基础上)以建立最优回归模型, 确保更准确地揭示试验数据和试验指标间的关系。
8) 自动试验优化 完成前述各项准备工作后, 即可在结果输出窗口得到回归分析的结果和优化的试验条件值。
2 结果与分析 2.1 4因素6水平试验结果按表 2试验设计接种各外植体, 2周后观察愈伤组织生长状态, 以黄绿色、富有光泽、结构疏密有致、最早出愈为最佳, 以褐色、最迟出愈为最差, 其余类推。综合各项指标分别以1.0~0.0序列标准予以量化, 取各试验组合平均数得到如下结果, 以第6组为佳(表 3)。
|
|
经均匀设计软件计算机处理, 并将数据予以常用对数转换, 得到如下回归方程:y= b (0) + b (1) lgX (1) + b (2) lgX (2) + b (3) lgX (3) + b (4) lgX (4)。第1方程项(因素1) :2, 4-D; 第2方程项(因素2) :NAA; 第3方程项(因素3) :6-BA; 第4方程项(因素4) :部位。
回归系数:b (0) = 3.21E-1;b (1) = 1.36E-2;b (2) = 3.87E-1;b (3) =-4.06E-1;b (4) = 2.05E+0。
标准回归系数:B (1) = 2.12E-2;B (2) = 7.33E-1;B (3) =-2.38E-1;B (4) = 1.64E+0。
偏回归平方和:P (1) = 8.68E-5;P (2) = 2.28E-2;P (3) = 1.97E-2;P (4) = 8.98E-2 (均匀性偏差0.358 1)。
表 4回归显著性检验表明回归显著, Ft=113.21 > F0.05 (4, 1) =55.833, 复相关系数R= 0.998 9。
|
|
方程中各项对回归的贡献(按偏回归平方和降序排列) :P (4) = 8.98E-2, 偏回归平方和/回归平方和=24.6%; P (2) = 2.28E-2, 偏回归平方和/回归平方和=6.2%; P (3) = 1.97E-2, 偏回归平方和/回归平方和=5.4%; P (1) = 8.68E-5, 偏回归平方和/回归平方和=0.0%。
对回归贡献最低的第1方程项显著性检验:F=0.107 6 < F0.05 (1, 1) =39.863, 为不显著。
2.4 第2次多元线性回归模型建立按照分析, 剔除(第1次)不显著因素第1项即2, 4-D后, 相应的原来的因素2 (NAA)就变成了因素1, 因素3 (6-BA)就变成因素2, 因素4 (外植体)就变成因素3, 再进行下一步骤分析。得回归方程:y = b (0) + b (1) lgX (1) + b (2) lgX (2) + b (3) lgX (3) + b (4) lgX (4)。第1方程项:取常用对数; 第2方程项:取常用对数; 第3方程项:取常用对数。
回归系数:b (0) = 3.10E-1; b (1) = 4.00E-1; b (2) =-4.07E-1; b (3) = 2.09E+0。
标准回归系数:B (1) = 7.57E-1; B (2) =-2.39E-1; B (3) = 1.67E+0。
偏回归平方和:P (1) = 3.40E-2; P (2) = 1.99E-2; P (3) = 1.62E-1。
表 5回归显著性检验表明回归显著, Ft= 272.51 > F0.05 (3, 2) =9.161 8, 复相关系数R= 0.998 8。
|
|
方程中各项对回归的贡献(按偏回归平方和降序排列) :P (3) = 1.62E-1, 偏回归平方和/回归平方和=44.4%; P (1) = 3.40E-2, 偏回归平方和/回归平方和=9.3%; P (2) = 1.99E-2, 偏回归平方和/回归平方和=5.4%。
对回归贡献最低的第2方程项显著性检验:F (2) = 44.507 > F0.05 (1, 2) =8.526 3, 为显著。回归分析结束, 自动生成图 1。
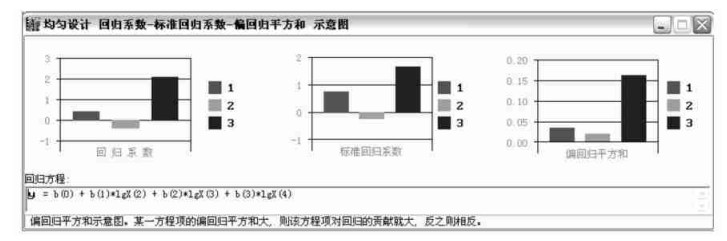
|
图 1 第2次回归分析示意图:回归系数-标准回归系数-偏回归平方和 Fig. 1 Sketch map about the second regression analysis: regression coefficient-standard regression coefficient-leaning regression square |
根据2次逐步回归, 并剔除不显著试验因素2, 4-D, 经试验优化后的结果:新因素1 (即NAA)的最优条件为2.000E+0;新因素2 (即6-BA)的最优条件为1.500E+0;新因素3 (即外植体)的最优条件为3.000E+0。预期试验愈伤组织诱导最大值:1.36E+0。最佳组合为MS+NAA 2.0 mg·L-1+6-BA 1.5 mg·L-1+芽。
2.6 试验验证按上述分析拟合得出的最佳组合是MS+NAA 2.0 mg·L-1+6-BA 1.5 mg·L-1+芽; 取银杏多年生植株当年生幼嫩茎段, 剪去叶片, 截取带芽外植体予以试验。结果除去被污染的部分, 愈伤组织诱导率100%, 培养5 d即出现愈伤组织, 生长旺盛呈黄绿或淡绿色, 富有光泽, 结构疏松充满活力。试验证明该配方对银杏芽培养的愈伤组织诱导效果很好。
3 结论与讨论本试验采用均匀设计, 通过建立试验方案、数据处理、回归分析, 以及优化拟合, 得到了最佳配方并予以了验证。根据试验结果和分析, 银杏外植体诱导的最佳组合是MS + NAA 2.0 mg·L-1+6-BA 1.5 mg·L-1+芽, 激素2, 4-D对银杏愈伤组织的诱导没有显著影响。如果仅仅按设计的直接结果确定第6组为最佳组合是不科学的, 因为该结果仅仅是本次6个组合中的1个, 不能覆盖所有试验。均匀设计区别于其他设计(胡惠露等, 2002; 韩凤梅等, 2004)的优越性在于它加大了试验的准确性; 作为只考虑试验点在试验范围内均匀散布的1种试验方法, 试验中应用了均匀设计法设置试验方案, 从全面试验点中挑选出部分代表性的试验点, 反映体系的主要特征, 本试验将本来要求46即4 096个组合数的试验只用了6个组合就可以了。利用均匀设计软件分析各种因素对银杏外植体诱导的生长效果的影响, 大大提高了试验效率。其他研究者的试验都曾说明了这一点, 如均匀设计可以优化纤维素酶解提取三七工艺(隋晓璠等, 2005), 均匀设计软件也是优化药用植物甘草(Glycyrrhiza uralensis)有效成分提取的一个非常有用的工具(张信青等, 2005), 等等。在大量的研究试验中(覃红, 2005; 徐松华等, 1998)均匀设计都显示其强大的功能。可以肯定的是, 采用合适的试验方法如均匀设计进行银杏组织培养, 对银杏工厂化生产及银杏遗传资源的保存和利用, 具有一定的学术价值和广泛的应用前景。
方开泰, 王元. 1994. 均匀设计与均匀设计表. 北京: 科学出版社, 69.
|
方开泰, 马长兴. 2001. 正交与均匀试验设计. 北京: 科学出版社.
|
韩凤梅, 姚向阳, 陈勇. 2004. 盾叶薯蓣纤维素酶酶解工艺研究. 化学与生物工程, (6): 26-27. DOI:10.3969/j.issn.1672-5425.2004.06.010 |
胡蕙露, 杨景华, 杨荻荣, 等. 2002. 银杏茎段试管培养条件筛选研究. 林业科学, 38(3): 52-56. DOI:10.3321/j.issn:1001-7488.2002.03.010 |
隋晓璠, 王超, 李永吉, 等. 2005. 均匀设计优化纤维素酶解提取三七工艺的研究. 中医药学报, 33(4): 8-9. DOI:10.3969/j.issn.1002-2392.2005.04.005 |
覃红. 2005. 混水平的均匀设计的构造. 应用数学学报, 28(4): 704-712. DOI:10.3321/j.issn:0254-3079.2005.04.014 |
王玉方.2003.试验设计与参数优化软件注册版[CP/OL][2003-06-11].http://www.advancedtechnic.cn/oldweb.
|
徐松华, 唐巍. 1998. 均匀设计在植物组织培养中的应用. 华南农业大学学报, 19(1): 21-23. |
张信青, 崔淑芬, 许柏球, 等. 2005. 应用均匀设计法优选甘草有效成分的提取条件. 中医药导报, 11(7): 4-6. DOI:10.3969/j.issn.1672-951X.2005.07.002 |
张瑛均匀设计网.2004.均匀设计的理论发展和均匀设计学会大事记[EB/OL][2004-07-23].http://www.cnoptimum.com.
|
Fang Kaitai, Wang Yuan. 1994. Number-theoretic methods in statistics. London: Chapman and Hall.
|
Fang Kaitai, Lin D K J, Winker P, et al. 2000. Uniform design:theory and applications. Technometrics, 42: 237-248. DOI:10.1080/00401706.2000.10486045 |
Fang Kaitai.2002.Some applications of Quasi-Monte Carlo methods in statistics//Fang Kaitai, Hickernell F J, Niederreiter H.Monte Carlo and Quasi-Monte Carlo methods in scientific computing.Berlin: Springer-Verlag
|
 2006, Vol. 42
2006, Vol. 42