滑索是指乘客沿钢丝绳靠惯性滑行的极限运动的游乐设施, 亦称溜索、速降、飞人等(国家质检总局, 2002)。滑索作为集游乐、体育于一体的富有刺激性的项目, 在全国迅速发展。滑索主要有以下3种类型:单(双)线无减速索有缓冲滑索型、单(双)线有减速索无缓冲滑索型和液压张紧中间下载滑索型。目前应用最多的滑索类型是单(双)线无减速索有缓冲滑索(图 1)。

对于滑索滑行速度(简称滑速)的理论研究, 目前国内外尚无完善的设计理论(沈勇, 2001), 滑索基本上是依靠经验架设。针对目前应用最多的单(双)线无减速索有缓冲滑索形式, 分析影响滑速的因素, 导出滑速的计算公式, 并将此理论应用于福建省三明市瑞云山滑索设计。最终通过对现场实测数据进行分析, 验证所研究的滑速理论是正确的。

1 滑索理论及技术关键 1.1 滑速

对滑索理论的研究, 是为了达到控制滑速的目的, 滑速是滑索设计的主要控制参数。作为一个大众参与的游乐项目, 其前提是必须保证乘客人身安全。合理的滑速, 既惊险刺激又安全可靠。滑速过大, 超出滑行者的心理承受能力, 容易导致不安全; 滑速过小, 则达不到刺激目的, 还可能导致乘客中途停滞而未达终点的事故。

1.2 滑索受力分析

滑索线路任意点的受力, 见图 2。由于荷重的作用, 车轮前后承载索被分为2段悬链线, 假设C点为全线路最低点, 由设计载荷Q(滑行小车和乘客)产生的切向力N₂, 使荷重沿AC滑行, 显然, 在车轮前方的前置坡度(升角)γ有阻碍车轮自由滑行的作用, 车轮轴承、车轮绳槽与承载索的摩擦形成摩擦阻力F₁起阻碍滑行的作用; 荷重(乘客)在高速滑行中, 由于空气及风的原因, 形成空气阻力F₂也起阻碍滑行的作用。

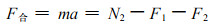
(1)

式中:N₂为由重力产生的下滑力, N₂=mgsinγ=Qsinγ。

滑行过程中受到车轮与钢丝绳的摩擦阻力作用。当滑行到最低点时, 升角为零, 继续滑行时, 升角由正值变为负值, 车轮将减速向B点滑行, 并以一定的末速度到达B点。

从滑行过程可知, 影响滑速的因子有跨距l₀、弦倾角α、无荷中挠系数S₀、设计载荷Q、车轮与钢丝绳之间的摩擦系数μ、乘客的出站初速度v₀、风阻做功A₃、支点位移量dl、温差dt、钢丝绳的规格参数。其中关键的因素为l₀、α、S₀、Q、μ、v₀、A₃。

1.3 滑索起、终点高差h₀及设计载荷做功A₁

当α、l₀确定时, h₀即确定, 乘客从起点(滑翔台)到终点(接收平台、降翔台)处的高差已确定。

(2)

设计载荷Q沿水平等分长度n内所作的功A₁为

(3)

式中:Q为设计载荷(N), Q=mg; g为重力加速度(m·s^-2), g=9.81;n为水平等分长度(m), 将水平跨距l₀分为z等分, 每等分长度n=l₀/z; γ为滑行小车(跑车)路径各等分点处悬索的升角(°)。

1.4 出站初速度v₀

乘客具有一定的出站初速度v₀, 那么, 乘客具有一定的初动能A₂为

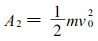
(4)

1.5 风阻做功A₃

在乘客下滑过程中, 有能量损耗。空气阻力是一个不可低估的因素, 风阻做功是一个变量, 是随滑行速度变化而变化的, 空气阻力与速度平方成正比。在乘客下滑速度达到一定时, 空气阻力是主要阻力。滑行速度越大, 风阻做功也越大。这里的风阻做功主要不是由于大自然风对乘客所做的功, 因为在《滑索安全技术要求(试行)》(国家质检总局, 2002)第28条规定:当遇到雨、雪、冰霜、雾及风速大于8 m·s^-1(4级)天气时, 不得运行。在滑索设计时, 必须考虑风向风速的影响, 应避免在常年风速较大和顺风区域建滑索。

空气阻力F₂, 计算式为

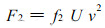
(5)

式中:v为相对运行速度, 即滑行速度与风速之差(m·s^-1);U为乘客迎风面积(m²), U的范围为0.3 ~ 1.0 m²(彼得罗夫等, 1984), 标准人正常滑行姿势选取U=0.7;f₂为空气阻力系数, f₂=Cp/v²=C/1.63(周军宏, 2001), p为风压, C为体形系数, 3级顺风, f₂=0.7, 3级逆风, f₂=0.8。

空气阻力F₂沿水平等分长度n内所作的功A₃为

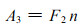
(6)

1.6 摩擦损失功A₄

车轮滚动摩擦阻力系数μ, μ与车轮的滚动轴承有关。当选择滚动轴承的极限转速小于或接近车轮实际转速时, 导致车轮与钢丝绳之间的滚动摩擦转变为滑动摩擦, 则摩擦阻力增大或轴承损坏, 乘客无法到达接收平台。

车轮的滚动摩擦阻力F₁计算式为

(7)

乘客重力对滑索产生的正压力N₁为

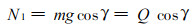
(8)

式中:μ₁为车轮轴承的摩擦系数(青铜轴套μ₁=0.06 ~ 0.01, 滚珠轴承μ₁=0.01 ~ 0.015);μ₀为车轮的滚动摩擦系数值(封闭索μ₀=0.3 ~ 0.4 mm, 敞露索=0.5 ~ 0.6 mm)。

当车轮半径R=100 ~ 125 mm时, 轮轴半径r对车轮半径R的比值是r/R=1/6 ~ 1/9, 推荐r/R=1/8。对于滚珠轴承, 单个车轮的μ=0.042 ~ 0.062;2个车轮的μ=0.062 ~ 0.082, 常取μ=0.007 8(东北林学院, 1984)。

设计载荷与承载索之间摩擦力沿水平等分长度n内所作的摩擦损失功A₄为

(9)

1.7 无荷中挠系数S₀

无荷中挠系数S₀是滑索的张紧尺度。S₀过小, 承载索预张力偏大, 从最高点到悬索最低点的高差及其势能变小, 使乘客的最大速度变小, 进站速度变大; 相反, S₀过大, 承载索预张力偏小, 从最高点到悬索最低点的高差及其势能变大, 使乘客的最大速度变大, 进站速度变小。S₀过大, 对于不同体重的乘客, 有可能无法到达接收平台。为确保乘客安全到达终点, 故无荷中挠系数S₀应取得小些。

2 滑速计算公式

设计载荷Q相对下支点具有一定的势能, 在滑行过程中势能转化为动能, 从起点站以步行速度(约v₀=0.5 m·s^-1)开始沿钢丝绳滑行, 逐渐加速到最大速度(12 m·s^-1左右), 而后逐渐减速并以安全速度(1 ~ 5 m·s^-1)进入终点站。根据动能定理, 将水平跨距l₀分为z等分, 即视滑索索长分为若干等分, 滑速由v₁变到v₂所引起的动能变化量为ΔE, 则设计荷重重力所作的功A₁开始时做正功, 从最低点往下支点滑行时做负功, 风阻做功A₃为负功, 摩擦阻力所作的功A₄为负功。即ΔE=A₁-A₃-A₄, 可求出任意点的跑车瞬时速度。运用系统功能原理(刘银春, 2001), 建立滑索运动的能量方程:

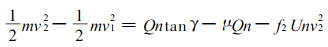
(10)

式中的升角γ由于承载索有设计载荷Q后, 由图 2知, 车轮升角是变化的。

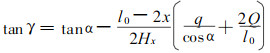
(11)

式中:x为跑车距下支点的水平距离(m); H_x为承载索水平张力(N)。

(12)

式(12)中各个变量含义见参考文献(周新年等, 1999)。式(10)中, 速度v₁、v₂采用依次递推计算。

3 滑索设计 3.1 主承载索设计

福建省三明市瑞云山风景区滑索, 应用悬链线理论(周新年, 1996;周新年等, 1999;2004), 编制计算机辅助设计系统, 输出结果。

各等分点的升角、水平张力、无荷挠度和有荷挠度计算结果略。

3.2 副承载索设计(略) 3.3 滑速计算

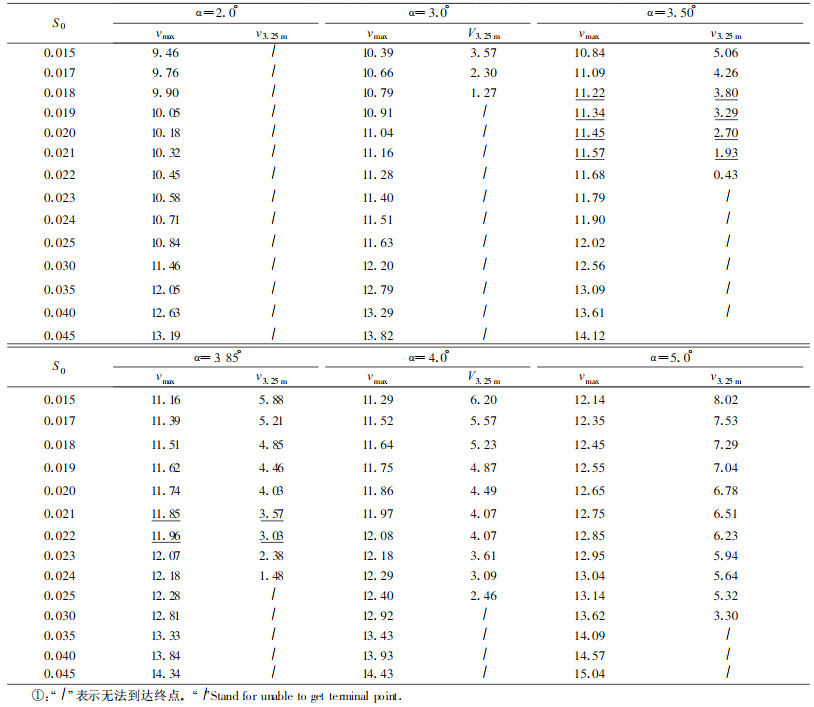
以极限速度为控制, 对承载索适宜倾角及无荷中挠系数进行选择。以初选Ф14.5 mm承载索, l₀=260 m, Q=750 N、v₀=0.5 m·s^-1、μ=0.007 8为例, 通过式(1)~ (12)的计算结果, 见表 1。

由表 1知, l₀ =260 m, S₀=0.018 ~ 0.021, α=3.50°; S₀=0.021 ~ 0.022, α=3.85°比较合适。

4 滑速试验及其分析

选用双索上下布置方式。主承载索选择:钢丝绳6W(19)+7×7-14.5-1700-GB/T 8918-1996;副承载索选择:钢丝绳6×19+1-12.5-1700 -GB/T 8918 -1996。Ф12.5 mm在上, Ф14.5 mm在下。安全系数:主承载索N=11.95;副承载索N=6.65。滑行小车采用双车轮(上、下轮)组合式, 见图 3。

当主、副承载索的无荷中挠系数均为S₀=0.021时, 出现滑行小车的主承载索车轮(下方)被悬空空转, 而副承载索车轮(上方)受力滑行。把副承载索Ф12.5 mm的钢丝绳放松, 即Ф12.5 mm的无荷中挠系数S₀取比Ф14.5 mm的略大3%~5%。这样, 主承载索承担主要负荷, 滑行小车运行平稳。一旦主承载索断掉, 副承载索也能起二次保护作用。

在风压500 Pa, 天气晴, 顺风, 风速v=4 m·s^-1, 对Ф14.5 mm的钢丝绳S₀=0.021、弦倾角α=3.85°、起点速度v₀=0.5 m·s^-1的不同载荷的v_max与进站速度v_z实测值, 见表 2。

可见, 实际测量值与理论计算值基本上相吻合, 这证明应用悬链线理论与物体运动动能定律相结合, 计算滑索的滑速是正确的。无荷中挠系数S₀在0.02左右, 较小的载荷(低于1 000 N)时, 载荷的大小对滑速的影响不大, 运行的平均速度较接近, 最大速度v_max＜12 m·s^-1, 使不同体重的乘客都可以安全到达终点, 且到达终点的速度不会过大(v_z≤5 m·s^-1), 再加上2套各自均能独立工作的制动装置, 2张防护垫作为缓冲装置, 可以保证安全。

5 结论

应用悬链线理论及物体运动动能定律相结合导出的递推滑速理论公式, 助推起点速度约为0.5 m·s^-1, 最大滑速控制12 m·s^-1左右, 进入终点安全速度1 ~ 5 m·s^-1为宜; 滑索的承载索采用双绳, 其直径不小于12 mm; 滑行小车采用两组绳轮且须二次保护。经用雷达测速仪实测与理论计算滑速比较, 其误差均小于1%。三明市瑞云山风景区滑索于2002年7月由国家质量技术监督局审查验收, 运营至今已2年多, 安全可靠。实践证明, 所提出的滑索设计理论是正确的。