生态位理论是生态学中最重要的基础理论和核心思想之一(Whittaker，1975；曲仲湘，1986；王伯荪，1987)，在生态学研究的诸多领域被广泛应用，并对生态学的许多核心问题做了成功的解释。在运用生态位理论进行生态学机理分析的过程中，一个十分重要的问题就是生态位参数的定义及其测度的问题。能够刻画生态位特征的参数有很多种，但较为常用的指标主要有2个：生态位宽度和生态位重叠。本文主要对迄今为止物种或种群生态位宽度与生态位重叠的计测模型进行综合分析与评述，提出生态位宽度和生态位重叠的新定义及若干测度模型。

1 生态位宽度模型 1.1 生态位宽度的基本内涵

生态位宽度(niche breadth)又称生态位广度(niche width)(van Valen, 1965; Mc Naughton et al., 1970)、生态位大小(niche size)(Willson, 1969)。各生态学家对生态位涵义的认识不同，对生态位宽度的内涵也有不同界定，如：在资源有限的多维空间中被一物种或一群落片段所利用的比例(van Valen, 1965)；在生态位空间内，沿着某一特定样线所通过的“距离"(Levins, 1968；MacArthur, 1968)；种内生境多样性权重的平均值(Pielou, 1971)；被一个有机体单位所利用的各种资源的总和(Pianka, 1976)；物种利用或趋于利用所有可利用资源状态而减少种内个体相遇的程度(Hurlbert, 1978)；物种或种群生态专化性的倒数(Kohn, 1968)；种群的表现型内和表现型间2种组分在资源轴上获得资源的区间长度(Roughgarden, 1972)；种群利用资源的概率分布与可利用资源的概率分布之间的相似程度(Feinsinger et al., 1981)；物种沿资源轴可以持续生存的值域(Crawley, 1986)；物种或种群对于生态资源的利用频度(Krebs, 2001)。为了使生态位宽度能涵盖实际生态位和基础生态位2种情况，本文将生态位宽度定义为物种或种群适应环境和利用资源的实际幅度或潜在能力。

生态位宽度的概念为进化生态学的许多假说提供了基础(Feinsinger et al., 1981)。物理环境、可利用的资源以及竞争者的有无，在生态的或进化的时间尺度内影响着一个种群生态位的宽度(Cody, 1974; Hespenheide, 1975; Levins, 1968; MacArthur, 1972; May et al., 1972; Roughgarden, 1974a; Sih, 1977; Wilson, 1976)。如果2个种群拥有同样的资源基础，其中1个种群的个体成员采用与资源的可利用性成比例的方式利用资源，另外1个种群的个体成员集中利用某些资源的某些组分(items)，而掠过其余资源的其他组分，那么，前1个种群的生态位宽度就大于后1个(Colwell et al., 1971; Cody, 1974; Levins, 1968)。研究生态位宽度的各种影响因素，有助于分析物种或种群的专化(specialization)与泛化(generalization)取食行为进行分析(Pianka, 1976)。

最优采食理论(optimal foraging theory)预言：当资源的可利用性减小时，生态位宽度应该增加(MacArthur et al., 1966; MacArthur, 1972; Schoener, 1971)。在食物供应不足时，较宽的生态位可以使消费每个食物单位时获得最大回报，因此，生物趋于泛化取食；而在食物丰富的环境中，可能导致生物选择性采食和狭窄的生态位宽度。一个竞争者能够在多大程度上压缩或扩大另一个种的现实生态位，取决于它是均匀地还是以斑块的方式利用资源。前者可能导致生态位扩大，后者可能引起生态位缩小。

尽管包括Pianka(1976)在内的许多生态学者都认为生态位宽度的概念在反映物种或种群的生态学特征方面是极为有用的，但也有人认为这一概念实际上并不能充分反映生态位结构，因为生物的分布与利用之间并不完全吻合(刘建国等，1990)。虽然这种质疑在某种程度上不无道理，但在目前尚无其他更为有效的指标或方法来替换它之前，保留总比抛弃更为可取。

总之，生态位宽度反映物种或种群对环境适应的状况或对资源利用的程度。但由于不同学者对其关注角度不同，他们所提出的生态位宽度测度模型也呈现出多样化的特征。

1.2 生态位宽度计测模型 1.2.1 Levins(1968)模型

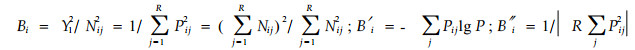
式中：B_i，B′_i，B″_i是物种i的生态位宽度；P_ij=N_ij/Y_i为物种i利用资源状态j的个体占该种个体总数的比例；R是可利用资源状态的数目。B_i是Simpson(1949)指数的倒数；而B′_i即是Shannon-Wiener指数(Shannon et al., 1949)。该公式计算方法简捷，生物学意义明确，但也存在不足：1)测定结果在很大程度上取决于所考虑的资源种类的多少，因此，很难使测定程序标准化，不利于对同一群落或不同群落中的物种生态位进行比较研究(Colwell et al., 1971)；2)没有考虑到资源的可利用性(a vailability)(Feinsinger et al., 1981; Hurlbert，1978; Petraitis，1979)；3)当资源状态合并时，生态位宽度会减小，这对于该公式来说是一个不好的性质(Petraitis，1979)。4)当采用上述公式计测生态位宽度时，其最大值出现在所有资源项目(item)被同等利用的情况下。当资源不是同样可利用时，专化种似乎比泛化种具有更宽的生态位。这显然与泛化种的生态位宽于专化种的通常观点相悖(MacArthur，1972)。Levins(1968)为回避这一棘手问题，假设所有资源的可利用性均相等。然而，大量研究表明这是无理假设，会影响计测结果(Hespenheide，1975; Pianka，1975)。为克服这些缺点，一些学者提出了改进公式或新的计测公式：Cody(1974)建议把资源的可利用性包括在公式中；Colwell等(1971)提出了对观测资料进行标准化的方法；Schoener (1974)和Hurlbert(1978)提出用资源的可利用性作为物种对资源利用度的加权。遗憾的是，这些计测方法不能通过统计方法加以检验(Petraitis，1979)。

1.2.2 Schoener(1974)模型

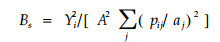
式中：B_s为第S物种的生态位宽度；A为所有可利用的资源状态多度之和；a_j是可利用的资源状态j的多度；其余字母意义同前。该公式的优点是考虑到了资源的可利用性，但它也有两点不足：1)如果不能按照生物本身所能区分的程度进行资源状态划分，B_s值就会有所改变(Feinsinger et al., 1981)；2) B_s缺乏适当的生物学意义(Hurlbert, 1978)。

1.2.3 Hurlbert(1978)模型之一

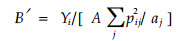
式中字母意义同前。这一公式具有通用性，因为它允许资源状态多度a_j可变。该式与Levins(1968)式具有相同的解释。该式的取值范围在1/n(当只有一个资源状态被利用时)与1. 0(当每个资源状态被利用的程度与其资源多度成比利时)之间。种对稀有资源的选择性很敏感，因此，式中给了一个较大的权重(Smith，1982)。但当a_j=0时，B′无意义。

1.2.4 Cowell等(1971)模型

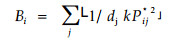
式中：P_ij^*2含义相当于P_ij；d_j是第j个资源状态的相对权重因子；k是把原来的R个资源状态扩展为k个资源状态的值(一般k＝10 000)。标准化后，该式还可以得到几种变型。

1.2.5 Petraitis(1979)模型

式中：W₁为度量生态位宽度的统计量；λ为最大似然比，它是观测的相对概率与最大相对概率之比，其表达式为：λ₁=L(n/q)/L(n/p)=Π(q_j/p_ij)^n_ij，其中q_j为环境中资源状态j出现的概率; p_ij为物种i利用资源j的概率; L为相对似然函数。

1.2.6 Feinsinger等(1981)模型

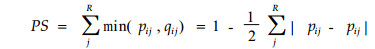
式中：p_ij意义同前；q_ij为物种i可利用的资源状态j占整个可利用资源的比例。该式是Czekanowski指数，或称比例相似系数，曾被用于计测生态位重叠(Colwell et al., 1971)及群落的相似性(Whittaker, 1975)。PS取值在0.1(当种群以与资源的可利用性成比例的方式利用资源时得到的最大值)到minq_ij(当种群专化利用稀有资源状态而掠过其它资源状态时得到的最小值)。

1.2.7 Smith(1982)模型

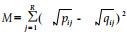
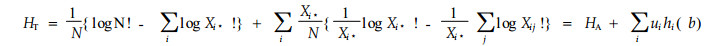
该式的取值范围为0~1，而且是距离的函数，式中p_ij、q_ij分别是第i个种群在第j个资源位上所占比例和资源利用效率，R为资源位个数。该式在计测物种对稀有资源的选择反应时不敏感。在资源利用向量为多维、资源可利用性固定且已知的情况下，可进行统计检验(Smith, 1982)。FT_i还可用于度量2个或1组物种间的生态位重叠。

1.2.8 Pielou(1971)模型

式中：N为总个体数；X_i*为C个生境中第i个种出现的频率；h_i(b)为第i个种的生境多样性；u_i为第i个种占的比例；为平均生态宽度；H_A为种的多样性；H_T为总的多样性。该式在实际计算时，并不需要任何关于生态位的正规定义，同时，可进行不同地理环境内2个种间的生态位比较。但这种方法只有当动物栖息生境可分为明显不同的亚生境时才是有效的(Pielou，1971))。

上述计测公式虽然由不同研究者提出，但有些公式之间存在数学上的联系。Petraitis (1981)用代数学和几何学方法讨论了5种生态位宽度计测公式间的联系：设二元函数g(a, b)=[Σp_i(p_i/q_i^b)^a-1]^1/(1-a)，则当a, b取值不同时，分别表现为不同的公式形式：g(0, 0)=R; g(1, 0)=exp(B'); g(2, 0)=B; g(1, 1)=B_p; g(2, 1)=B_H; g(2, 2)=B_s。式中B, B', B_p, B_H, B_s分别为Simpson指数的倒数、Shannon指数、Schoener(1974)指数、Hurlbert(1978)指数及Petraitis(1979)指数；R为资源状态的数量。可见，上述5个公式之间的区别仅在于a，b赋值的不同，亦即给p_i和q_i所赋权重的不同。

1.2.9 映射函数模型

王刚(1984)将生态位定义为从环境状态集合A={x|x=(x₁, x₂…x_n)}到物种y的密度集合的映射函数f(x₁, x₂…x_n)>0。在此基础上，y在x_i轴上的生态位宽度，即是点集A_i＝{x|Prjf(x₁, x₂, …x_n)>0}的测度m(A_i)，n维向量W=[m(A₁), …, m(A_i), …, m(A_n)]^T就是y在n维生态因子空间的生态位宽度。

1.2.10 多维生态位宽度计测方法

物种或种群生存于多维生态因子空间，因此，基于多维生态位宽度测度，才有更多实际意义。20世纪70年代后，多元统计分析方法的应用为多维生态位计测方法带来突破。

Green(1971；1974)采用多元判别分析方法计测多维超体积生态位，并提出了度量生态位宽度的新方法：在判别因子空间内，样本观测的置信椭圆在某一给定判别因子轴上的投影长度；M'Closkey(1976)以生态位椭圆沿单个轴的种内判别值标准差作为生态位宽度；Dueser等(1979)以种在判别空间内距原点的平均欧氏距离作为生态位位置、变异系数作为生态位宽度。

秦玉川等(1994)采用主成分分析方法研究了橘园内几种螨类及其天敌间的营养生态位关系，并采用种群95%等密度概率椭圆的面积或体积计算生态位宽度。Yu等(1992)、余世孝等(1994)认为生态位宽度可以用物种在生态位空间各分室的分布状况来表示。在二维生态位空间内的生态位宽度可用I_B=1-2I₁₂/2I_max度量，进一步扩展后，可度量多维生态位宽度。

李德志(1995)采用主成分分析和典范分析方法研究了森林群落中主要组分种群间的生态位关系，并对群落结构进行了分析。在计测种群的多维生态位宽度时，采用简捷的方法，把多个单维生态位宽度值整合：

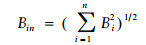
式中：B_in为多维生态位宽度；B_i为第i个生态因子轴上的生态宽度；n为生态因子轴个数。该式在各轴间相互独立时成立。但实际上，由于各生态因子轴间通常具有互补性或依赖性，难以保证完全独立，故直接以B_in式计算多维生态位宽度存在一定误差(但在精度要求不高的情况下尚可)。如能通过适当数学方法建构新轴并使轴间独立，再采用该式则较为合理。

1.3 生态位宽度计测模型的发展趋势

生态位宽度计测模型种类很多(上述模型并非全部)，但在应用过程中，只有那些方法简捷、生物学意义明确的模型被广泛而长期使用；而那些形式繁琐、生物学意义含混的模型，逐渐被淘汰。基于单一资源轴的生态位宽度计测研究目前在国内还属多数，但随着多维生态位计测在方法上的不断突破，今后，多维生态位研究将会受到更多关注，而多元统计分析方法将在其中扮演重要角色。

2 生态位重叠模型 2.1 生态位重叠的基本内涵

生态位重叠是生态位计测过程中的一个重要指标。许多学者曾经对此给出不同定义，如：2个物种对某一资源的共同利用程度(Cowell et al., 1971；Abrams，1980)；2个物种在同一资源状态上的相遇频率(Hurlbert，1978)；一定资源状态上物种的多样性程度(Pielou，1971)；2个物种与其生态因子联系上的相似性(王刚，1984)。为了使生态位重叠能够涵盖实际生态位和基础生态位2种情况，本文将生态位重叠定义为2个或多个物种或种群在适应环境和利用资源的实际幅度或潜在能力方面所表现出的共同性或相似性。

资源分享的数量或生态位重叠是理论生态学研究的中心问题之一(Pianka, 1976)。生态学家们长期以来一直困扰于2个种的生态学特征究竟可以相似到多大程度而仍然可以共同生存？竞争排斥法则、特征替位、极限相似性、种填塞以及最大容许生态位重叠等概念都是在这一问题的启发下构建起来的(Hutchinson，1957; Schoener，1965; MacArthur et al., 1967; MacArthur，1969; 1970; May et al., 1972; Pianka，1972)。一些数学模型的运算结果表明：当竞争种类数量增加时，最大容许生态位重叠应当降低，并接近于衰减指数(Pianka，1974)。May等(1972)预言：最大容许生态位重叠应该对环境的变化不敏感。

建立在L-V方程基础上的许多生态位模型，迄今已经产生了若干可检验的预测结果(MacArthur，1970; 1972; May et al., 1972; May, 1974; Roughgarden, 1974b; 1976; Roughgarden et al., 1975)。生态位重叠值常常被用作L-V方程中竞争系数的估计(Brown et al., 1973; Culver, 1970; May, 1975; Orians et al., 1969; Pianka, 1969; Schoener, 1968)。这种处理虽然可能较为方便，然而，将生态位重叠与竞争系数等同，可能值得怀疑并容易引起误解(Colwell et al., 1971)。只有资源利用上的重叠，并不能保证会发生竞争，因为竞争依赖于可利用资源的数量和种群的大小(Slobodchikoff et al., 1980)。虽然生态位重叠是利用性竞争的一个必要条件，但重叠并不一定会导致竞争，除非资源供应不足。此外，干扰性竞争也不大可能形成，除非在对有限资源的利用过程中有发生重叠的可能，因此，避免竞争可能会导致资源利用模式的完全非重叠, 即:间隔生态位(disjunct niche)。Pianka (1976)认为：生态位重叠本身对于干扰性竞争而言，既不是必要条件，也不是充分条件；而重叠对于利用性竞争而言，只是必要条件，而不是充分条件。许多事实证明：竞争与生态位重叠之间，经常可能是一种相反的关系。有关生态位重叠的假说认为：最大容许生态位重叠在强烈竞争的情况下，比在需求/供应比率相对较低的环境中要低(Pianka, 1972)。当然，这一假说尚有待进一步证实。

有关生态位重叠的现有理论和模型，大多基于单个资源维度(May, 1974)。很显然，只有更多关注物种或种群间的多维生态位重叠，才能揭示出它们之间全面的生态关系。

2.2 生态位重叠的计测模型 2.2.1 曲线平均模型(Price, 1975; Schoener, 1968; 1974)

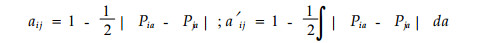
其中：a_ij和a′_ij分别为适用于离散型和连续型数据的生态位重叠；P_ia和P_ja分别代表种i和种j中利用资源状态a的个体数。该2式旨在计测不同种利用资源的概率分布的相似程度，形式与计测生态位宽度时采用的PS模型一致，但字母含义不同。其优点为：1)从离散数据向连续数据的转化简单；2)计算方法简便，并使用于超过一维资源的情况。但从一维转换到多维，存在数学和观测上的困难(Slobodchikoff et al., 1980)。

2.2.2 对称α模型(Pianka, 1973)

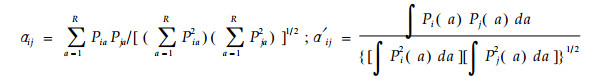
其中：α_ij和α′_ij分别为适用于离散型和连续型数据的生态位重叠(α′_ij要求连续变化的资源a被均匀分割)；P_ia和P_ja意义同前。对称性α法的特点：1)明确的几何学解释；2)所产生的矩阵具有对称性质；3)α值不会超过1(Slobodchikoff et al., 1980)。

2.2.3 非对称α模型(Levins, 1968；MacArthur，1972)

式中字母意义同前。α″_ij矩阵是非对称的，一般α″_ij≠α″_ji(May，1975)。当物种i比j更为常见时，α″_ij < α_ij＝α_ij < α″_ji(α_i和α_ij由对称α模型得到)。α″_ij反映物种j对物种i的竞争压力，因此，它对L-V方程中竞争系数的估计要比α_ij好。因α″_ij式对个体数量反应敏感，研究者必须小心查数相关物种个体数。当物种j能够比i更成功地逃避观察者时，α″_ij的计测值将表明物种j对i的竞争压力较小，但事实并非如此。当比较不同资源类型时，情况更加复杂，因为物种针对不同资源类型，可能采取不同方式来逃避观察者，因此，比较不同α″_ij值十分困难(Slobodchikoff et al., 1980)。

2.2.4 和α法与积α模型(Cody, 1974；May, 1975)

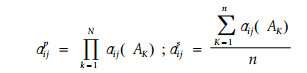
式中α_ij^p是物种i和j的积α，它采用沿每个资源轴的α值的乘积形式。α_ij^s是物种i、j的和α，它是一个简单的平均数形式。α_ij(A_K)是第K个资源A上的α_ij值。Cody(1974)和May(1975)认为积α模型通常可用于独立的资源，而和α可用于非独立的资源。

2.2.5 信息函数模型(Horn，1966)

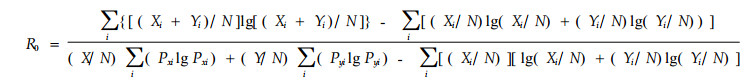
式中R₀为2个种群间以信息函数表示的生态位重叠；N = X + Y，其余字母意义同前。模型以Shannon-Wiener的信息函数为基础而提出，旨在减少因资源被任意分割成各资源状态而产生的误差。Colwell等(1971)对此作过详细说明。

2.2.6 似然估计模型(Petraitis，1979)

Petraitis(1979)提出的2个可直接进行统计检验的方法是专化重叠与泛化重叠。前者与Levins(1968)提出的测度公式在意义上相一致，而后者与Pianka(1973)提出的修正式在意义上相一致，并与Horn(1966)公式相关。非标准的专化重叠模型：

式中Φ₁₂和Φ₂₁分别表示物种1对2和物种2对1的非标准的专化重叠。其余字母意义同前。Φ₁₂或Φ₂₁的取值为0~1；-2ln Φ符合χ²分布，df=r-1。Φ作为非标准化的度量值，对于n值变化敏感。Φ要求两物种必须利用所有的资源状态。物种h与k之间的非标准化的泛化重叠模型：

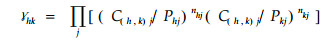
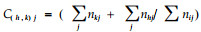
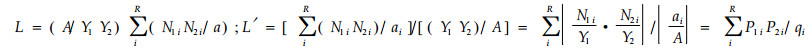
式中; P_nj、P_kj意义同前。泛化重叠模型可用于多个物种。值域为0~1。-2ln γ符合χ²分布，df=(S-1)(r-1)。

2.2.7 概率比模型(Hurlbert，1978)

式中N_1i、N_2i分别是利用资源状态i的物种1和2的数量；a_i是资源状态i的可利用性(加权因子)；A是所有资源可利用性之和；Y₁、Y₂分别是物种1和2的个体总数。L ′是L式的变型。通过q_i加权可以减少因资源状态可利用性差异造成的计测误差。2式取值有时会大于1。2式比其他早期模型更具合理的生物学解释，但当计测生态位重叠只用于描述目的时，此前的若干生态位重叠公式似乎比L′或L式更好(Abrams，1980)。L和L′式假设物种对资源状态的利用与资源多度成比例，其正确性也值得怀疑(Petraitis，1979)。

2.2.8 种间缀块指数模型(Lloyd，1967)

式中字母意义同前。

2.2.9 方向性重叠计测模型(Lloyd，1967)

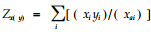
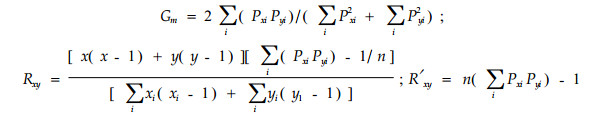
Z_x(y)为物种y对物种x的平均拥挤度；其余字母意义同前。Hurlbert(1978)称该式是一个好的测定指标。当资源状态多度a_i变化时，上式变成“共同出现系数”(Rathke，1976)：(表示物种y平均与物种x的一个个体相遇的概率密度)。

2.2.10 Morisita指数模型(Morisita，1959；1971)

C_m式(Morisita，1959)具对称性，并与Pianka(1973)式相似。R_xy和R′_xy (Morisita，1971)分别在重叠值比独立性假说预测值大和小时采用。其余字母意义同前。

2.2.11 积-矩相关系数模型

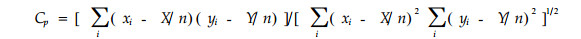
式中字母意义同前。该式即为Pearson相似系数，广泛用于植物群落中种间联结关系测定(Hurlbert，1978)。Goodall(1973)认为该式和曲线平均模型可能最适合计测生态位重叠。

2.2.12 百分比重叠指数模型

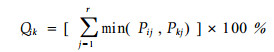
该式形式简明并便于解释，通常称为Schoener(1970)指数。

2.2.13 映射函数法

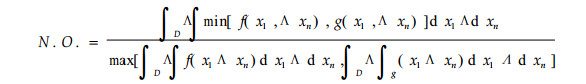
式中N.O.为生态位重叠(王刚，1984); f(x₁, x₂…x_n), g(x₁, x₂…x_n)分别为2个物种的连续型生态位(离散情况可依此类推)。该式具有几何上的直观解释，并且在计算生态位重叠时，采用种群密度绝对值并引入生态因子间隔参数。

2.2.14 集合论模型

该式是本文以集合论为基础提出的物种或种群间生态位重叠计测模型。涵义是2个物种或种群生态位(物种的生态因子适应曲线与生态因子轴间包围的面积)的交集与2个物种或种群生态位的并集之比。式中字母意义同前(离散情况可以此类推)。该模型能较好地反映2个物种或种群生态位间的数量关系。

2.2.15 生态位重叠间接计测模型：生态位分离计测模型

1) 余世孝等(1993)把一个种的生态位超体积假定为可以再分割。各子空间的中点到生态位空间的中心点的距离设为D_j，则2个物种i和k之间的生态位分离为h个加权的绝对差值之和。

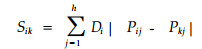
式中：S_ik为种i和k间的生态位分离；P_ij和P_kj分别为种i和k在中点坐标为(x_1j, x_2j, …, x_μj, …, x_nj)的第j个子空间的分布比例量；x_μj为第j个子空间中点在μ个资源维上的坐标；n为生态位空间维数。若第μ个资源维划分梯度数为m，则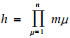；S_ik≥0，当2个种具有一致的分布时，S_ik值最小(0)；当2个物种具有完全不同分布时，S_ik值最大。

2) 本文提出一个新的用于计测生态位分离的模型：2个物种或种群沿同一生态因子轴分布的生态位中心位点距，它可作为生态位重叠的间接计测：

式中:ΔC_p为2个物种或种群生态位中心位点距；C_pi与C_pj分别为物种或种群i和j的生态中心位点；X_i, Y_i与X_j, Y_j分别为C_pi与C_pj的坐标值。

2.2.16 生态位重叠间接计测模型(资源分离比率模型)：

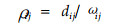
式中：d_ij为物种i和j资源利用平均值之差；ω_i和ω_j分别为2个物种资源利用曲线的标准差；ω_ij为2个物种资源利用曲线的共同宽度：ω_ij=[(ω_i²+ω_j²)/2]^1/2。该模型用于计测生态位分离(Southwood, 1978)，是生态位重叠的间接测度。

2.2.17 多种群生态位重叠模型

Petraitis(1979)建议采用下列模型计测多种群的生态位重叠：

式中：n_ij、N、P_ij的含义同前；c_j为第j个资源状态的相对多度。

2.2.18 多维生态位计测模型

Green(1971; 1974)把通过多元判别分析方法得到的生态位椭圆相交面积占2个物种累计面积的百分比作为多维生态位重叠；Pappas等(1997)把通过典范对应分析得到的2个种在生态位空间内的概率椭圆的重叠作为多维生态位重叠；秦玉川等(1994)把通过主成分分析方法得到的2个种群间的生态位椭圆(或椭球)相交面积(或体积)占2种群累积面积(或体积)的比值作为生态位重叠系数；李德志(1995)把2个种群在各单维生态因子轴上的生态位重叠值整合，得到多维生态位重叠估计值：

式中：NO_n为种群i和j的多维生态位重叠；O_ij(a)为种群i和j在生态因子轴a上的生态位重叠值。该式在各轴间相互独立时成立，但在一般情况下，也可以该式粗略估计多维生态位重叠。基于本文提出的生态位分离度模型ΔC_p，多维生态位空间内的分离度计测模型为：

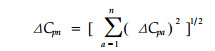
式中：ΔC_pn代表n维生态位空间内的生态位分离度；a代表某生态因子轴；n代表生态位空间的维数。该式在各维间相互独立时成立，但在一般情况下，也可以该式粗略估计多维生态位分离，并作为对多维生态位重叠的间接计测。

2.3 生态位重叠计测模型的发展趋势

生态位重叠的测度模型种类繁多(上述模型并非全部)，但在应用过程中被普遍接受的模型首推形式简捷、生物学意义明确的模型。迄今为止，基于单一资源轴的生态位重叠计测研究在国内尚属多数，但随着多维生态位计测方法的日臻成熟，特别是多元统计分析方法在生态位研究领域内的不断应用，多维生态位重叠计测将会受到更多关注。