树高是林业上极为重要的测树因子之一。一直以来, 由于其测定工作量繁重, 不论在生产还是科研中都很难对大量树高进行测定; 但是人们对追求树高测定的简单高效尝试却一直没有停止过。立体视觉技术给人们提供了重建单木任意部位直径树高的便捷方法。对于林分而言, 如何解决遮挡成为立体恢复的瓶颈问题, 这也是图像处理与计算机视觉上难于解决的问题之一, 它关系到三维重建的成败。纵观目前用于解决遮挡问题的方法大致可分为2类:一类是极线最优方法(Geiger et al., 1995; Bobick et al., 1999), 这类方法是在一对极线上计算通过所有匹配像对的最短路径, 部分遮挡的问题通过由一幅图像的多个像点与另一副图像的一个像点匹配来解决; 另一类是全局最优方法(Scharstein et al., 1998; 2002; Boykov et al., 2001; Sun et al., 2003), 这类方法是首先在整个图像上定义一个包含数据误差、模型约束以及遮挡在内的能量函数, 然后采用最优化的方法获得全局最优的视差图。从结果来看, 一般是全局最优方法要优于极线最优方法, 但是其计算量也较大。这2类方法对树高的重建都很难有理想的结果, 至少表现在3个方面:首先, 郁闭林分在图像中就是相互遮挡的林分, 对于某一株树梢端的确定异常困难; 其次, 由于受风的影响, 树梢在不同图像中所成像点可能表现的是空间中不同的位置; 再次, 欲在一帖图像收入高大的乔木势必加大摄影距离从而相对增加匹配难度, 同时用于树高重建的梢端树基通常处于图像的2个边缘, 可能受更大的镜头畸变影响。鉴于林分图像的实际情况, 本文提出通过重建枝下高并结合干曲线预估树冠高的方法。

1 重建方法 1.1 重建策略

在研究单木模型时通常会使用一些默认的假设, 比如树木越高直径越小, 树干边缘连续并满足某种干曲线形式, 树木上任意垂直树干的截面为圆形等, 这些条件基本上能够满足林业需求。认真观察林木会发现树木的高矮H由下部直径d及树干边缘与铅垂线所呈倾角α的大小决定, 即满足下面的函数关系

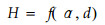
(1)

很明显, 下部直径越大倾角越小, 树木越高, 就是说树高与直径及树干倾角有某种必然联系。基于这种考虑, 本文把树干分成枝下高与树冠高2部分, 枝下高部分由立体视觉方法重建其高度及倾角、直径等内容, 冠高由得到的枝下高部分的倾角及直径根据式(1)构造得出, 最后将两部分高度之和作为最终的立木树高。图 1给出了求算树高的执行路线。

1.2 枝下高相关数据的三维重建

摄像机定标后, 其内参数K就已经确定, 如果保持两摄像机状态不变, 则外参数也可在重建中使用, 就说是在3D空间中使第2个摄像机坐标系与第1个摄像机坐标系重合所需要的旋转矩阵R和平移向量t可以在3D恢复中使用。

令两摄像机内参数为K₁、K₂, 其对应关系R、t, 则匹配的图像点(h₁, h₂)所对应的空间点坐标X能够由式(2)表示(王雪峰等, 2005; 松山隆司等, 1998)

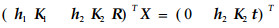
(2)

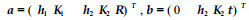
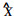
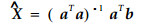
当, 则X的最小二乘解为

(3)

其中: 是内参数, (u_i, v_i)是图像点坐标, i=1, 2。

大多情况下, 在远离图像中心会有较大的畸变, 描述非线性畸变可用式(4)表示(Weng et al., 1990),

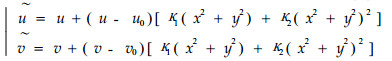
(4)

式中:κ₁、κ₂是镜头畸变参数, 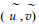是实际图像坐标, (u, v)是理想图像坐标, (x, y)是正规化图像坐标, 即(x y 1)=K^-1(u v 1)^T。

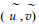
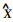
至此, 在2台摄像机姿势固定情况下求空间坐标的步骤如下(i=1, 2):标定摄像机, 得到a_xi, a_yi, c_i, u_0i, v_0i, κ_1i, κ_2i, R, t; 由实际图像坐标利用式(4)计算理想图像坐标(u, v); 由式(3)计算空间点坐标。

需要注意的是, 由于已经正规化, 重建时K_i中c_i应该置0;对于a_xi=a_yi的CCD摄像机, 标定时二者可能并不相等, 当利用正规化后图像坐标重建时, 可以令或(a_xi+a_yi)/2, 本文例子使用了前式。

1.3 冠高预测与获取立木高

对干曲线的研究至少有上百年的时间。目前, 对干形较为一致的看法是树干自基部向稍端的变化大致归纳为:凹曲线体、圆柱体、抛物线体和圆锥体(孟宪宇, 1996), 由此引起树干边缘对应倾角的相应变化, 在对冠高的推算中应该考虑这种变化。下面给出倾角与直径及树高的关系。

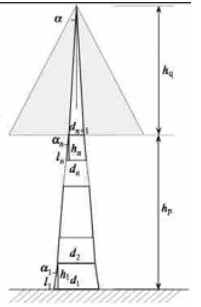
用n+1水平面把枝下高h_p部分树干从树基开始分割成n个小段(图 2), 其水平面直径分别记为d₁、d₂、L、d_n、d_n+1; 所分割成的树高分别为h₁、L、h_n, 遮挡树高h_q; 树干左侧小段斜边长l₁、L、l_n, 左侧树干边缘与铅垂线形成的夹角为α₁、L、α_n。

令, 故

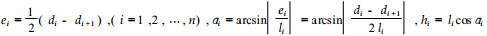
(5)

现在的关键问题是确定梢端α角。本文例子中的水杉(Metasequoia glyptostroboides)、银杏(Ginkgo biloba)树种干型饱满, 通体接近圆锥体, 因此, 可以用圆锥体来近似模拟这类树干。理论上, 过圆锥体轴心切面切圆锥体形成的三角形斜边与铅垂线所呈的倾角是固定值, 但由于树干的不规则, 直接取枝下高部位某一角度值来估计树冠高可能会带来很大误差, 所以用下面一系列倾角平均值来代替梢端α角。

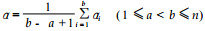
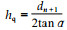
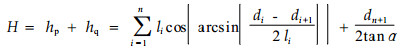
取, 有, 进而得到完整的树高

(6)

实际计算中, 倾角非常小(比如 < 10^-8)的截面间高可以直接取斜边长, 其他部分截面间高可由勾股定理计算, 即

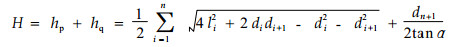
(7)

重建过程中, 树干右边缘各直径处匹配点已经存在, 所以能够同样计算右边缘的各长度、角度及对应累积高度、树冠高。通常情况从左右两边缘求得的结果往往不相等, 可以取二者平均值作为最终的结果。

需要说明的是, 本文中通过枝下高数据估计树冠高部分, 但实际操作并不需要严格按着林学中规定的枝下高定义来做, 仅是使用枝下高部位相关数据而已。很明显, 树冠高部分没有遮挡的树干直径也可以作为估计全树高的基础数据。

2 重建实例与结果

为解决被动立体视觉树高重建中树冠的遮挡问题, 本文采用了结合干曲线的方法; 为了验证其可行性有必要尽可能减少其他影响, 事先对2台摄像机进行固定并完成了定标工作, 其定标结果如表 1。

试验图像取自中国林业科学研究院内木化石附近的几株树木(图 3), 其中3、5号树是水杉, 其他为银杏。为增加已知信息, 在样地内插了一根花杆。现在的目的是重建树高, 由于树冠的相互遮挡, 直接根据梢端与基部重建树高是困难的, 因此在图像采集过程中并没有摄树木全体, 而是仅取了枝下高部分。

按着前述思路, 在每株待恢复树高立木的枝下高不同部位分别重建了4个直径, 其中一个在树基部。在求匹配点过程中, 首先对图像进行了去噪、Canny检测, 然后通过交互式方式给出直径位后由机器按最大灰度相关法找出匹配点, 至此就可进行3D重建。重建出中间点后, 计算点间欧式距离得到诸直径值及相邻直径端点连线距离, 进而得到树干边缘左右两侧各倾角。由于树干基部干形变化大, 倾角也大, 所以在求算冠高的参数中不宜使用此倾角。本文是把上端2个倾角平均值做α、最上面的直径为d_n+1, 按式(7)计算左右两侧树高取平均值作为最终的树高, 结果见表 2。

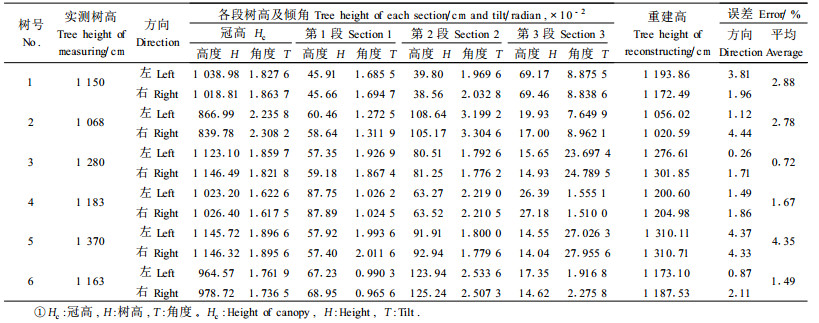
表 2中的实测树高是激光测树仪测定结果, 重建高是冠高与前3段高度的合计, 误差=100×|重建高-实测树高|/实测树高。从结果看, 最大误差4.35%是5号树, 3号树的误差最小, 是0.72%, 包括左右方向在内的所有误差均小于5%, 这表明立体视觉与干曲线结合重建遮挡林木的树高是可行的。

3 讨论

遮挡是机器视觉研究中的难点内容之一, 在三维重建中它所带来的直接问题就是难于图像匹配。本研究避开了树梢部位匹配困难的难点, 采用了通过重建便于图像处理及匹配的枝下高相关数据、结合干曲线方程恢复树高的方法, 实例证明是可行的。以下几点值得做进一步研究:

1) 文中采用上端的2个倾角平均值作为最终计算冠高的角度值。根据人们研究所得的树干变化规律, 如果枝下高很高, 直接使用最上端的倾角可能会得到更为准确地结果。

2) 例子中的水杉、银杏树种通常干型饱满, 通体接近圆锥形, 所以本文用枝下高部分树干倾角平均值作为树梢的倾角, 本方法对具有这一干型特征的树木具有通用性。如果干型变化很大, 应该考虑采用适合该树种的干曲线, 否则会带来更大的误差。出于这一考虑, 探讨不同树种枝下高的不同部位直径与树高的关系具有重要的实际意义。

3) 本研究在所有距离的重建过程中都涉及到匹配问题, 寻找适合于树木图像匹配的算法有重要的实际应用价值。