Bamboo, with a long tradition in China, is one of the emerging sectors in the Chinese economy. It is making an increasingly large contribution to farmers' income and playing an important role in rural industrial development (Ruiz-Prez et al., 2001). Bamboo is characterized by faster growth, quicker maturity and higher production than wood. Its mechanical properties are similar to wood and some ones even better. Bamboo is in some cases a substitute for wood as building and decorating materials.

Moso bamboo (Phyllostachys pubescens) is the most important bamboo species in China. There are 42 000 km² of bamboo forest in China and moso bamboo alone covers about 30 000 km², which is about 2% of the total Chinese forest area (Fu, 2001). Bamboo has low natural resistance and suffers easily from moth-eating and mildewing. Therefore, it needs to be treated with preservatives before being used. Water-soluble reagents are most widely used in the chemical treatment of bamboo timber (Wu, 1992), and therefore, knowledge of water adsorbability of moso bamboo is useful. Some workers have done investigations on moisture content and adsorbability of moso bamboo. Zhou (1981) examined the moisture content and water adsorbability of moso bamboos. The wetting contact angles of various liquids on moso bamboo surface and some factors affecting wettability of bamboo surface were reported by Chen and Hua (1992). Jiang et al. (1995) established the relationship between the height and age on moisture content of standing moso bamboo and equilibrium moisture content of moso bamboo wood.

The purposes of the present research is to investigate water penetration of moso bamboo, to establish an empirical equation for estimating the quantity of water penetrated into moso bamboo specimens with immersing time, and to discuss the judgement in the maximum mass of water penetration.

1 Materials and methods

Four groups of moso bamboos aged one year, two years, three years and four years grown in Fuyang, Zhejiang Province were tested. Bamboo aged two and three years is the mainly used one. Each group included four air-dried bamboo woods. Five specimens without nodes were cut from each bamboo wood with the beginning two meters above the ground and an interval of one meter. Specimens were longitudinally 40.0 mm in length and tangentially 20.0 mm in width. The thickness of specimens was that of the bamboo culm.

Oven-dried mass of each specimen was measured after they were held in an oven at 103 ℃ for 20 hours before immersed in water. Specimens were put in containers filled with clean water at atmospheric pressure and room temperature. The immersed specimens floated on water in the early stage and sank within two to four weeks. Mass of the immersed specimens was measured every day in first five days of the penetration and every week from the day when they had been immersed for seven days. After the average increment in their mass of a group of specimens was not larger than 0.015 g, they were weighed every two weeks. Weighing for a group of specimens ended up when naught increment in mass was recorded.

Specimens were wiped up with dried cotton before weighing. Measurement of mass was made by using an electronic balance with a readability of 0.001 g (Sartorius BS300S-WE1). Water in containers was refreshed every day and kept a constant depth of six centimeters during the penetration. Due to a curvilinear cross-section of bamboo wood, swelling volume of each specimen was measured by the method of water volume replacement when water penetration finished (Hu, 1984). Then the basic density of specimen was calculated.

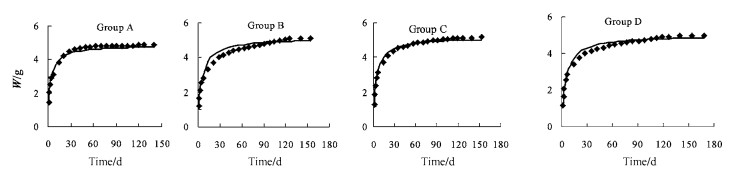
2 Results and discussion

Water uptake in a specimen is the difference between its oven-dried mass and the immersed one. Results are plotted in Fig. 1 for averages of water uptake against the immersion time from group A, B, C, and D with age class of one year, two years, three years, and four years respectively. It can be seen from these figures that water uptake in specimens increases very rapidly in the early stage of penetration and then the increment became smaller gradually in a comparatively long immersion time toward a maximum. According to Tan (1992), water uptake vs immersion time can be expressed by an empirical equation as

(1)

where W (g) and t (day) are the water uptake and immersion time; a, b, and c are constants. Rearranging Eq.(1), it turns into

(2)

It can be found from Eq.(1) that W reaches a maximum of 1/a when immersion time t approaches to infinity. Therefore, constant a in Eq. (2) will be able to be determined provided that the maximum water uptake (MWU) in specimen is know. Water in bamboo specimen includes bound water and free water (Petty et al., 1969; Wu, 1992). The maximum water uptake can be written as

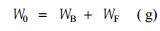
(3)

where W_B (g) and W_F (g) are the maximum of bound water and free water in specimen.

W_B is equal to the product of the density of bound water (ρ_S) and the volume of bound water at fiber saturation point (FSP) (V_B). According to definitions of FSP and moisture content, W_B can be also expressed as the product of the moisture content at FSP (m_F) and oven-dried mass of specimen (M₀). Thus the volume of bound water in specimen is

(4)

The volume of free water in specimen is

(5)

where ρ_F is the density of free water (g·cm³) and V_F is the volume of free water.

The sum of V_B and V_F should be the total volume of voids (V₀) in specimen and it can be expressed as (Siau, 1984)

(6)

where ρ_B (g·cm^-3) and ρ_W (g·cm^-3) are the basic density of specimen and the density of cell wall; V_S (cm³) is the swelling volume of specimen. The V₀ considered here is the total volume of voids in swelling specimen (Hou, 1992), so the basic density and the swelling volume of specimen are used in Eq. (6) instead of the oven dried density and oven-dried volume done originally by Siau(1984).

Inserting W_B = ρ_SV_B and W_F = ρ_FV_F into Eq. (3) and eliminating V_B and V_F from Eq. (3) with Eq. (4), (5), and (6), and the equality of V_F= V₀-V_B, W₀ can be written out in the form

(7)

According to Wu (1992), the main chemical compositions of bamboo are alike to those of woods; except without ray cell, bamboo has the same cells as hardwood, such as vessel, fiber, and parenchyma; there is similar way of water penetration for bamboo and wood. Therefore, it is assumable that differences between properties of bamboo and wood should be equivalent to ones within different woods. 1.46 g·cm^-3 has been used as the density of cell wall for all kinds of woods (Siau, 1984), so the value is taken as the density of cell wall (ρ_W).

The stronger the adsorptive force between water and substance of cell wall is, the higher the FSP is (Skaar, 1988). The density of bound water becomes large because water molecules are compressed due to the adsorptive force from substance of cell wall (Quirk, 1984). 0.24 can be assumed as FSP of moso bamboo reported by Wu (1992). Such a FSP falls in the lower bound of FSPs for different woods cited by Stamm (1964). That indicates that the force is low between water and substance of moso cell wall and the density is also low for bound water in moso specimen. Therefore 1.014 g·cm^-3 (Quirk, 1984), which is obtained from measurement on hardwood and lower than other ones (Kellogg et al., 1969; Beall, 1984), is regarded as the density of bound water in moso bamboo.

The density of free water ρ_F has no relation to the medium which free water is held in (Siau, 1984) and it is 1.0 g·cm^-3, the one of liquid water. With the results from the tests and the parameters mentioned above, the calculated values of W₀ from Eq. (7) are figured out.

Let y =1/W and x=1/t and substitute both for 1/W and 1/t in Eq.(1) yielding

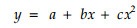
(8)

y is equal to a and W to W₀ when t approaches to infinite, and a is given as 1/W₀. The constant b, and c are obtained by the method of polynomial regression with the given value of a (Alder et al., 1977). Calculation for the regression is performed in Excel with a set of W and t from experiment. Values of constants a, b, and c, and the correlation coefficients are listed in Tab. 1. The correlation coefficient is calculated by its definition (Tan, 1992), and a is given as 1/W₀.

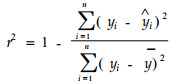
(9)

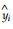
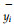
where y_i =1/s_i; = predicted values of y_i; = average of y_i; t_i=the immersion time; n = sample number of pairs (y_i, t_i).

Results from the empirical equations for MWU in specimens are also shown in Fig. 1. The correlation coefficients listed in Tab. 1 are all close to 0.966~0.990 indicating a very strong correlation considering the sample number of pairs n is in the range from twenty-three to twenty-five (Fang et al., 1988).

The fraction of water uptake in specimen can be calculated by dividing the volume of water uptake at immersion time t by the total volume of voids in specimen (Siau, 1984), and it can be expressed as

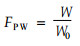
(10)

There are differences in water uptake for each specimen in one group at the given immersion time. F_PW describes the state of void in specimen filled with water and it will be more useful than W in practice, especially for the preservative treatment. Calculated values of F_PW can be obtained by Eq.(1), (7), and (10). Data in Tab. 2 are the values from measurement (F_PW1) and ones from calculation (F_PW2). Measured and calculated maximum mass is respectively used as W₀ in both calculations. Results show that there is a reasonable agreement between F_PW1 and F_PW2. Such an agreement means that Eq. (7) and selected values of ρ_W and ρ_S can work well in the calculation for both W₀ and F_PW.

The increment of water uptake in specimen becomes smaller with the increasing of immersion time, especially in the case that water uptake is very near to MWU. A proper balance should be used to determine MWU. Seemingly a more exact result will be obtained using a more precise balance. However, for the size of specimens we used, it is not meaningful to use a balance with a readability of 0.000 1 g or less. This is because a variation in mass more than 0.000 1 g is indicated from the result of calculation and measurement due to water evaporation on surface of specimen.

Water evaporation can be estimated from Fick's law

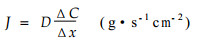
(11)

where D is diffuse coefficient (cm²·s^-1) and ΔC/Δx is concentration gradient (g·cm^-4).

Air close to specimen surface is saturated with water and absolute humidity (AH) in the saturated air is 17.3 g·cm^-3 at 20 ℃ (Siau, 1984). The relative humidity inside room in daytime is between 60% and 85%, which correspond to AH between 11.3 g·cm^-3 and 14.7 g·cm^-3. In consideration of the outer space of one centimeter away from the surface of specimen, there will be a water concentration gradient of 2.6~6.1 g·cm^-3. Diffuse coefficient of water in air is 0.270 cm²·s^-1 at one atmospheric pressure and 20℃ (Cussler, 1984). Inserting these values into Eq.(11), mass of diffused water from specimen surface (28 cm²) in ten seconds is 0.000 2~0.000 46 g. A continuous decrease in mass was also recorded up to about 0.000 6 g within ten seconds when a specimen was weighed by a electronic balance with a readability of 0.000 1 g at room temperature. It is hard to determine when varying reading is given out on the balance. However, a balance with a readability of 0.001 g gives an invariable reading when the same specimen is weighed. Therefore, for the sizes of specimens used in this study a balance with a readability of 0.001 g is able to meet the precision limited by water evaporation for practical application. The maximum water uptake in specimen can be considered to be reached once the difference in mass is less than 0.001 g between two successive weighing.

MWU varied among groups with different age classes, but there is no relationship between it and the age, and MWU bears no relation with the immersion time too. However, there existed a relationship that group with older age took longer time to get its MWU. Jiang et al. (1995) investigated the correlation between the moisture content in standing moso bamboo and its age. They found that the moisture content decreased with increasing age and that there was a significant correlation between both. The moisture content in standing bamboo indicates the maximum quantity of water being held in bamboo. The result in this work is consistent with Jiang et al.(1995).

The results from our tests showed that about 90% of the voids in specimen has been filled with water after the specimens were immersed in water for five weeks. It can be predicted that it takes five weeks to fulfil the chemical treatment with water soluble preservatives for moso bamboo in the size of the specimens for this study. As shown in Tab. 2, F_PW1 (F_PW2) is larger than 0.5 in seven day's immersion, and therefore, a week may be enough to fulfil the chemical treatment on surface layer of moso bamboo timber sized as the specimens.

The predicted MWUs are all larger than the measured ones (seen in Tab. 2). The phenomenon can be explained by two possible reasons. First, the predicted values are the limits when the immersion time approaches to infinity, but the measured values are determined from the experiment in a finite immersion time. Second, water penetrates into bamboo body and occupies the void that is filled originally with air. The void can only be occupied completely by the penetrated water and the predicted maximum mass achieved if air is totally removed from voids, which Petty and Preston (1969) found to be impossible.

3 Conclusion

MWU and its corresponding immersion time of moso bamboo varied with age. Specimens with older age took a longer time to reach its MWU. About 90% of the voids in specimens were filled with water after the penetration had been executed for five weeks.

An empirical equation can be established for the water penetration into moso bamboo by polynomial regression, with which MWU and the corresponding immersion time can be predicted.

Accuracy of weighing was limited by the mass decrease caused by water evaporation from immersed specimen surfaces.